|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fantoni tiene licencia CC BY-NC 4.0 |
|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fantoni tiene licencia CC BY-NC 4.0 |
|
|
La gran pintura esbozada en la parte superior derecha de la pared del fondo de Las Meninas
está inspirada en la copia del discípulo de Diego Velázquez, Juan Bautista Martínez del Mazo,
del óleo original firmado por Jacob Jordaens que se conserva en el Museo del
Prado.
Jacob Jordaens compuso su lienzo, pues, hacia 1637 a partir de un boceto sobre tabla de Rubens de la colección del Museo Real de Bruselas [1].
|
|
Tmolo corona a Apolo ante Pan y Midas
Dimensiones: 26,7375 × 38,3625 centímetros
11,5 × 16,5 pulgadas
Óleo sobre tabla - Peter Paul Rubens - 1637
Museo Real de Bruselas - Número de catálogo - 4128 |
|
Tmolo corona a Apolo ante Pan y Midas
Jacob Jordaens
Museo del Prado - Número de catálogo - P001551 |
 |
| Autor |
Número de Catálogo |
Medidas del Catálogo |
Reajuste |
Sistema castellano |
Ratio |
| Jacob Jordaens |
P001551 |
1,80 × 2,70 metros |
1,798 × 2,697 metros |
77 y 1/3 × 116
pulgadas |
1,5 |
|
|
 |
|
|
Velázquez, copiando la copia de su discípulo Mazo en sus Meninas, homenajeaba indirectamente a dos de los pintores más relevantes del norte de Europa, a Pedro Pablo Rubens, y a su discípulo Jacob Jordaens convertido al calvinismo en 1648.
En el Catálogo del año 1936 el título del tema de estos cuadros era Apolo vencedor de Marsias, y, afortunadamente para el análisis de estas dos pinturas, disponemos, pues, de las medidas del lienzo original de Jordaens y las de la copia de Mazo para ser estudiadas con la máxima precisión.
 |
|
|
Como hemos indicado, la copia de Mazo fue copiada de nuevo por Velázquez en Las Meninas, donde se halla esbozada en la parte superior derecha de la pared del fondo, no obstante, en este análisis utilizaremos las medidas de la copia de Mazo como ayuda para averiguar la verdadera envergadura de esta pared lejana, por lo que convertiremos el tamaño en metros de este óleo al sistema de medidas castellanas.
En la siguiente tabla mostramos la modificación que hemos hecho de las medidas del Catálogo, y esta corrección es tan leve que debemos considerar estas nuevas medidas castellanas iguales a las del tamaño original del lienzo de la copia del pintor Mazo.
| Autor |
Número de Catálogo |
Medidas del Catálogo |
Reajuste |
Sistema castellano |
|
Juan Bautista Martínez del Mazo |
P001712 |
1,81
× 2,25 metros |
1,8135
× 2,232 metros |
78
× 96 pulgadas |
|
|
 |
|
|
|
Las medidas exactas de la copia del pintor Mazo tienen la utilidad práctica de poder ser convertidas además en unidades, un procedimiento que nos facilitaría analizar a la pared del fondo de Las Meninas con rotundo verismo [2].
Planteamiento:
El gran cuadro derecho de la pared del fondo de Las Meninas se pinta con marco.
Aunque se pinte con marco el gran cuadro superior derecho de Las Meninas no es óbice para hablar de proporcionalidad.
Los márgenes visibles dan como prueba que Velázquez se inspiró en el formato de la pintura de su discípulo Mazo.
El centro del rectángulo que analizamos tiene por coordenadas:
[X = 18,75 ; Y = 15]
 |
|
|
Tamaño del cuadro superior derecho
|
Unidades |
Tamaño en la rejilla de trabajo |
Sistema métrico |
Pulgadas reales |
Sistema métrico |
||||
|
Altura |
25,8 unidades |
22
pulgadas y 14/15 |
= |
0,5332 metros |
86 |
= |
1,9995 metros |
|
|
Anchura |
31,2 unidades |
27
pulgadas y 11/15 |
= |
0,6448 metros |
104 |
= |
2,418 metros |
|
|
Adecuación en la distancia del cuadro de Mazo sobre la rejilla de trabajo
|
Coeficiente de ampliación |
Medidas castellanas |
Sistema métrico |
|||
|
Altura |
23,4 unidades ×
3,333333...
pulgadas por unidad |
= |
78
pulgadas |
= |
1,8135 metros |
|
Anchura |
28,8 unidades ×
3,333333...
pulgadas por unidad |
= |
96 pulgadas |
= |
2,232 metros |
|
|
El tamaño de la moldura del cuadro superior derecho
En la siguiente imagen se detalla las dimensiones exactas que hemos obtenido del tamaño de la anchura de esta moldura pintada en Las Meninas.
 |
El ancho real de la moldura pintada mide 4 pulgadas. |
|
|
Basado en el tamaño del Pie Real, pues, este sistema
de medición es el único procedimiento matemático posible.
La Vara Real de Burgos, en la época de la construcción del Monasterio del Escorial, estandarizó el sistema de medidas en la península Ibérica; y así lo confirma la pragmática dictada por el monarca Felipe II el 24 de junio de 1568 [3]:
Y declaramos que la vara Caſtellana de que se ha de uſar en todos eſtos Reynos, ſea la que hay y tiene la ciudad de Burgos.
|
|
|
El pintor Diego Velázquez ajustó sus mediciones de acuerdo al tamaño de la copia de Mazo.
0,3 unidades en la rejilla de medición equivalen en el mundo real de la pared del fondo a:
0,3 unidades × 3,333333... pulgadas por unidad = 1 pulgada = 23,25 milímetros.
La rejilla de trabajo es una herramienta válida para garantizar un sistema de equivalencias de medidas longitudinales.
Ciertamente, estamos cerca de conocer nuevos datos de Las Meninas.
|
|
|
|
Y del momento de preguntarnos;
¿en qué aposento o habitación del Palacio se pintan Las Meninas?
En el mismo siglo XVII este lugar del Alcázar [4], enumerado con el nº 25 en la Relación núm. 2 de la planta baja de palacio de Gómez de Mora, recibió distintos nombres, hemos recogido varios de ellos; la galería baja de mediodía, galería de la Reina y la Habitación del Príncipe [5].
Las dos estancias que nos interesan fueron descritas de esta guisa por el arquitecto del rey:
25 - galería de la Reyna que tiene bentanas Al jardín de la emperadores
12 - Apto donde come
|
|
|
|
Y refiriéndose a la misma estancia que analizamos, el crítico e historiador de arte Jonathan Brown, a partir de la investigación de Ángel del Campo y Francés en su libro: La Magia de Las Meninas. Editorial Ediciones Turner - 1985, oficializó la ubicación real de los dos grandes cuadros de la pared del fondo de Las Meninas [6]:
|
En cualquier caso, todos los intentos que se realicen en un futuro por buscar sentido a los cuadros dentro del cuadro, deberán tener en cuenta que ése era el emplazamiento real y auténtico de los mismos. |
Años más tarde matizó:
|
Asimismo sabemos que el cuadro estaba en una habitación privada del Rey, que no era una habitación de grandes dimensiones. Este dato conduce a una serie de preguntas. ¿Por qué encerrar un cuadro tan grande en una sala tan pequeña y tan privada? |
|
|
|
Gabinete de Dibujos y grabados del Museu Nacional d´Art de Catalunya - Barcelona |
Recordaríamos que fue el mismo pintor quien escogió, además de sus propios cuadros, las obras pictóricas más preciadas de los grandes maestros para ser colgadas en las paredes del Alcázar, es decir; Velázquez conocía muy bien sus dimensiones, ya que, como Aposentador, era responsable de la decoración interior, y ésta era, pues, una de las razones que le obligaba a conocer las regias medidas de los muros de Palacio.
 |
|
|
La información que aportamos promueve distintas maneras de resolver un mismo problema, y todas las soluciones conducen al lugar donde Velázquez pintó Las Meninas [7].
Hemos ya comprobado una forma efectiva de medir en la distancia, por lo que utilizaremos de nuevo la copia de Mazo como herramienta, y así averiguar el tamaño real de los elementos que se hallen en la sección del área del muro del fondo de esta pintura.
 |
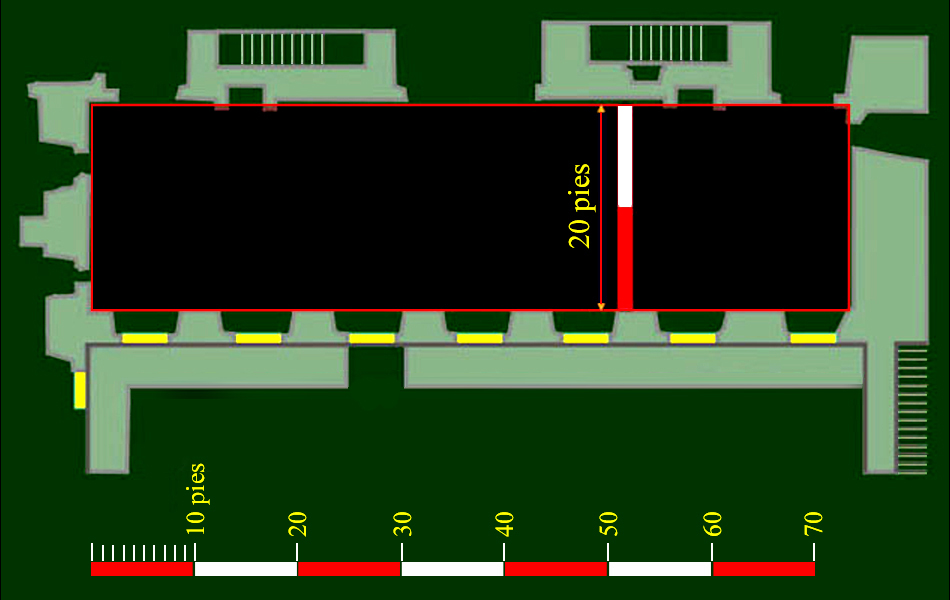
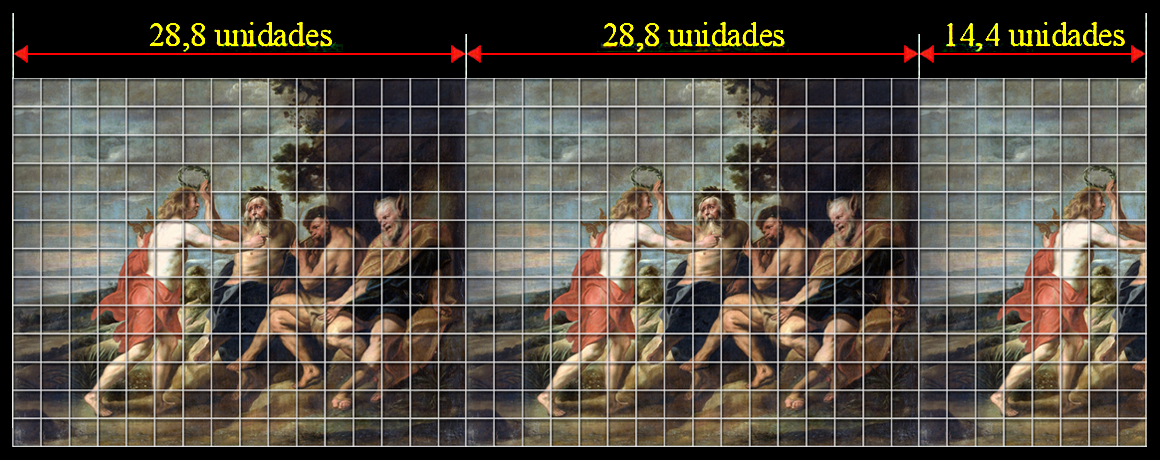
De manera, que en la distancia, 8 pies castellanos equivalen al ancho de la copia sin marco de Mazo sobre el cuadro superior derecho de la pared del fondo de Las Meninas, que corresponden, pues, a 28,8 unidades en la rejilla de medición.
El tamaño de 28,8 unidades posibilita medir el ancho de la pared del fondo, ya que 2 partes y media de esta misma medida completa el total del ancho de 72 unidades de esta pared que analizamos.
 |
Cierto, hay dos procedimiento para calcular la anchura real de la Habitación del Príncipe:
72 unidades × 3,333333... pulgadas por unidad = 240 pulgadas = 20 pies Castellanos = 5,58 metros,
y si multiplicamos el ancho real de 96 pulgadas del lienzo de Mazo por 2,5 obtendremos, pues, 240 pulgadas.
|
La distancia entre la vista y lo que se ve ha de ser proporcionada; ya que el tamaño de cualquier objeto o figura, aunque se localice muy distante, debe armonizar con la lejanía plasmada en el lienzo.
Y como indicó Francisco Pacheco, el maestro de Velázquez:
Así la distancia ha de corresponder a la vista con cierta razón y proporción de ángulos. |
 |
|
|
El libro de Las metamorfosis de Publio Ovidio Nasón inspiró a Velázquez en distintas ocasiones, pero en este caso que ahora analizamos el pintor quiso transmitir el significado de Misericordia o Gracia que esta esfera cabalística denominada Chesed, חסד, representa.
Cumplidamente, Quevedo, caballero de la Orden de Santiago del siglo XVII, de los más notable de la literatura española, prolífico escritor de narrativa y teatro, así como de textos filosóficos y humanísticos, hace un análisis etimológico del nombre de esta Sefira nº 4.
|
No ſin miſterio en la lengua Santa, que los brota aun en los puntos eſla palabra חֶסֶד, que ſignifica, miſericordia, piedad, beneficio, y bondad, ſignifica tambien oprobrio, coſa tan contraria: Empero verificaronſe todas ellas ſignificaciones en Chriſto, en quien el oprobrio fue piedad, miſericordia, beneficio, y bondad de חֶסֶד, ſe llama la cigüeña חֲסִידָה por ſer ſimbolo de la piedad, no ſin oprobrio, pues exercitando la piedad en la decrepitud de ſus padres, tiene por alimento las peſtes de la tierra, y comiendolas haze beneficio à los hombres, à quien ſon azechanza. |
|
Página 126 Obras Póstumas de don Francisco de Quevedo y Villegas Amberes. 1726 |
Oprobio, del latín opprobrium, significa; ignominia, afrenta, deshonra, y sus sinónimos; deshonor, vergüenza, humillación, agravio, baldón, injuria, vilipendio, infamia, un vocablo que permite comprender, pues, las consecuencias de la competición musical que Velázquez esboza en la pared del fondo de Las Meninas, donde Tmolo, el juez del concurso, da por vencedor a Apolo tañendo su lira ante Pan tocando su flauta, sin embargo, fue a Midas, por protestar, a quien Apolo le hizo crecer grandes orejas de asno entre los cabellos.
Estas orejas de la vergüenza las descubrió un barbero que acicalaba a Midas, y que, obligado a guardar su secreto, en un lejano valle cavó un pozo donde allí lo reveló, lo que prueba que la verdad no se puede ocultar a nadie.
Geométricamente, pues, planteamos un espacio diáfano en el que están anidados
cuatro escenarios de distintos formatos, en cuyo centro, en el
señorío de la Sefira nº 9, Yesod - El Fundamento, se hallan retratados los
monarcas en el Espejo.
 |
 |
|
|
| Anchura | escala | unidades | pulgadas | metros | ||
|
|
Habitación del Príncipe | 1/1 | 270 | 240 | 5,580 | |
|
|
Lienzo de Las Meninas | 1/2 | 135 | 120 | 2,79 | |
|
|
Pared del fondo | 1/3,75 | 72 | 64 | 1,488 | |
|
|
El Espejo | 1/20 | 13,5 | 12 | 0,279 |
El ancho del lienzo de Las Meninas mide la mitad de la anchura de la Habitación del Príncipe, y el tamaño de la anchura de la pared pintada equivale a 1/3,75 de esta misma sala.
Por lo que el ancho de la pared del fondo pintada en Las Meninas medirá en el sistema castellano:
240 pulgadas ÷ 3,75 = 64 pulgadas
8 × 8 pulgadas × 0,02325 metros por pulgada = 1,488 metros
Este modo de medir permite, sin lugar a la duda, a reconocer la anchura exacta del tamaño real de la pared del fondo de Las Meninas.
FORMATO 8
| Formato | Proporción | Pulgadas por unidad | Anchura | Tamaño en metros | |||||
| 8 | 8/9 | 0,888888 | × | 72 unidades | = | 64 pulgadas | 8 × 8 × 0,02325 = 1,488 metros | ||
|
|
| formato | proporción | escala | unidades | pulgadas | metros | |||
| 8 | 8/9 | = | 0,888888 | × | 72 | = | 64 | 8 × 8 × 0,02325 = 1,488 |
| 7 | 7/9 | = | 0,777777 | × | 72 | = | 56 | 7 × 8 × 0,02325 = 1,302 |
| 6 | 6/9 | = | 0,666666 | × | 72 | = | 48 | 6 × 8 × 0,02325 = 1,116 |
| 5 | 5/9 | = | 0,555555 | × | 72 | = | 40 | 5 × 8 × 0,02325 = 0,93 |
| 4 | 4/9 | = | 0,444444 | × | 72 | = | 32 | 4 × 8 × 0,02325 = 0,744 |
| 3 | 3/9 | = | 0,333333 | × | 72 | = | 24 | 3 × 8 × 0,02325 = 0,558 |
| 2 | 2/9 | = | 0,222222 | × | 72 | = | 16 | 2 × 8 × 0,02325 = 0,372 |
| 1 | 1/9 | = | 0,111111 | × | 72 | = | 8 | 1 × 8 × 0,02325 = 0,186 |
| 0 | 0/9 | = | 0,000000 | × | 72 | = | 0 | 0 × 8 × 0,02325 = 0 |
|
|
|
|
|
|
| Formato | Proporción | Pulgadas por unidad | Altura | Tamaño en metros | |||||
| 8 | 8/9 | 0,888888 | × | 60 unidades | = | 53,333 pulgadas | 8 × 6,666 × 0,02325 = 1,24 metros | ||
|
|
| formato | proporción | escala | unidades | pulgadas | metros | |||
| 8 | 8/9 | = | 0,888888 | × | 60 | = | 53 y 1/3 | 8 × 6,666 × 0,02325 = 1,24 |
| 7 | 7/9 | = | 0,777777 | × | 60 | = | 46 y 2/3 | 7 × 6,666 × 0,02325 = 1,085 |
| 6 | 6/9 | = | 0,666666 | × | 60 | = | 40 | 6 x 6,666 × 0,02325 = 0,93 |
| 5 | 5/9 | = | 0,555555 | × | 60 | = | 33 y 1/3 | 5 × 6,666 × 0,02325 = 0,775 |
| 4 | 4/9 | = | 0,444444 | × | 60 | = | 26 y 2/3 | 4 × 6,666 × 0,02325 = 0,62 |
| 3 | 3/9 | = | 0,333333 | × | 60 | = | 20 | 3 × 6,666 × 0,02325 = 0,465 |
| 2 | 2/9 | = | 0,222222 | × | 60 | = | 13 y 1/3 | 2 × 6,666 × 0,02325 = 0,31 |
| 1 | 1/9 | = | 0,111111 | × | 60 | = | 6 y 2/3 | 1 × 6,666 × 0,02325 = 0,155 |
| 0 | 0/9 | = | 0,000000 | × | 60 | = | 0 | 0 × 6,666 × 0,02325 = 0 |
|
|
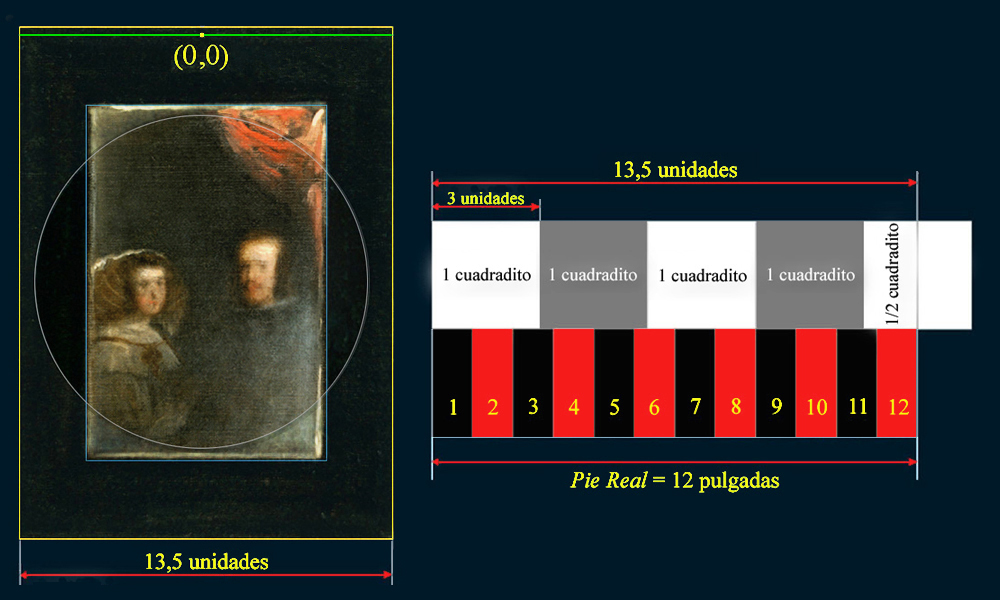
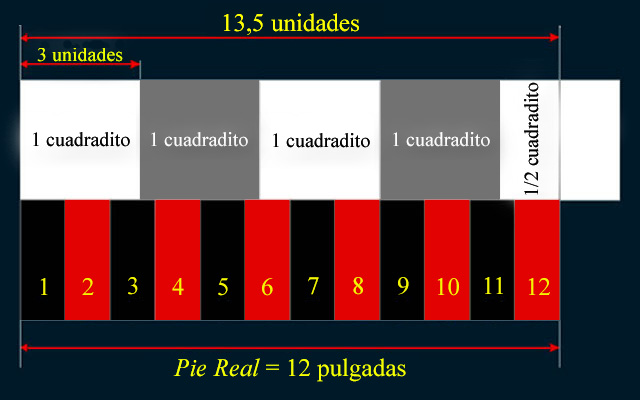
En la cuadrícula de trabajo el Pie Real
equivale a 4,5 cuadraditos, y sabemos, además, que sobre esta misma rejilla
4,5 cuadraditos es lo que mide la anchura del Marco del Espejo.
El Pie Real, el legítimo patrón de medidas castellano, ejerce el control absoluto sobre las medidas del lienzo de Las Meninas, y quedó puntualmente representado en la misma anchura del espejo pintado en esta obra de arte.
La anchura del Marco del Espejo mide 1 Pie Real.
 |
|
|
En la cuadrícula de trabajo una pulgada equivale a 1,125 unidades, por lo que si multiplicamos 1,125 unidades por 12 obtendremos 13,5 unidades, que es la cantidad de unidades que equivalen 4,5 cuadraditos en esta cuadrícula.
Las 12 pulgadas del ancho del Espejo equivalen, pues, al Pie Real, y también al tamaño de 12 pulgadas del lado de un Pentágono regular.
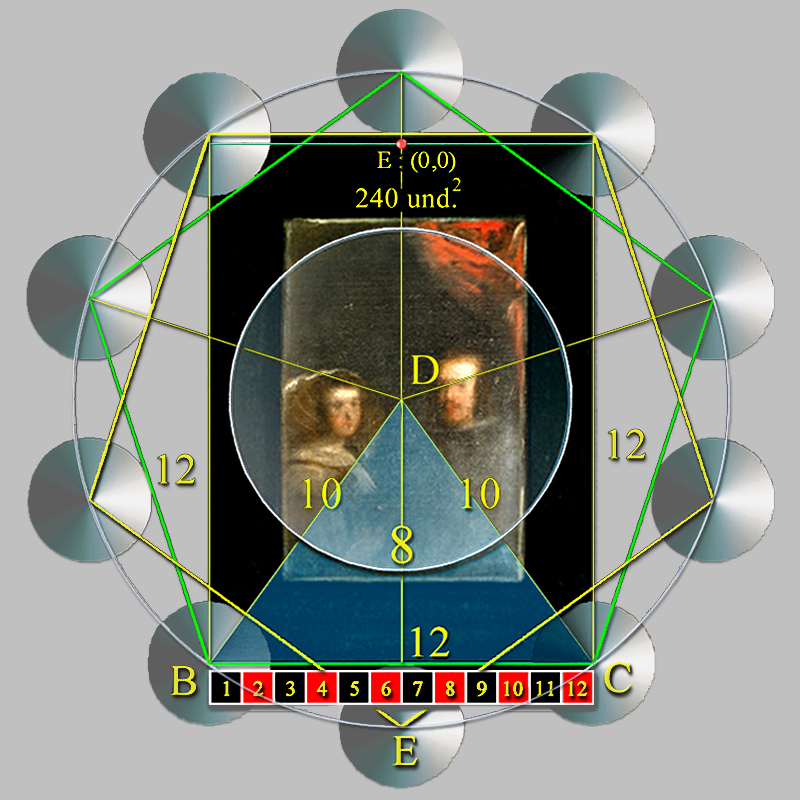
Si bien, Velázquez situó, en cuatro de los 10 vértices de un decágono regular formado por dos pentágonos superpuestos, las cuatro esquinas del Espejo, que determinaron, pues, el formato del ancho y alto del marco de madera del Espejo.
 |
|
|
De modo, que a partir de este esquema, Velázquez disponía en el Espejo a la Sefira nº 9, Yesod, el Fundamento, donde el rey Felipe IV y la reina Mariana de Austria refrendan, desde entonces, una Alianza divina.
Y no hay ninguna duda de que el pentágono y el pentagrama son figuras geométricas que en la Geometría Sagrada simbolizan tanto la proporción divina como la unificación entre el mundo inferior y el superior.
La excelencia de la maestría geométrica velazqueña sería aún más palpable en el supuesto de que a partir del centro del Espejo se trazara la figura de un decágono regular de una unidad de lado, el cual, no sólo determinaría las cuatro esquinas del marco del Espejo, sino que, además, el tamaño del radio del círculo circunscrito equivaldría al número áureo Phi; Φ = 1,618033...
|
|
|
√(2 + Φ) = √(2 + 1,618033...) = 1,902113... |
En un decágono regular de una unidad de lado la relación entre el radio DB del círculo que lo circunscribe y su lado BE, por ejemplo, están en proporción áurea.
Velázquez propone esta relación matemática al utilizar, como tamaño del ancho del Espejo, el lado de un pentágono 6,308774... veces mayor, de manera, que sus cálculos dependieron del número áureo en la anchura exacta de 12 pulgadas del marco del Espejo.
|
|
Sobre el papel, 6,308774... veces mayor corresponde, pues, al tamaño BE del lado de 6,308776... pulgadas del decágono que circunscribe al Espejo de Las Meninas.
En la siguiente imagen se muestra la concepción del Espejo en el área geométrica de una quinta parte de un pentágono regular, cuyo lado BC de 12 pulgadas corresponde al tamaño de la anchura del marco del Espejo.
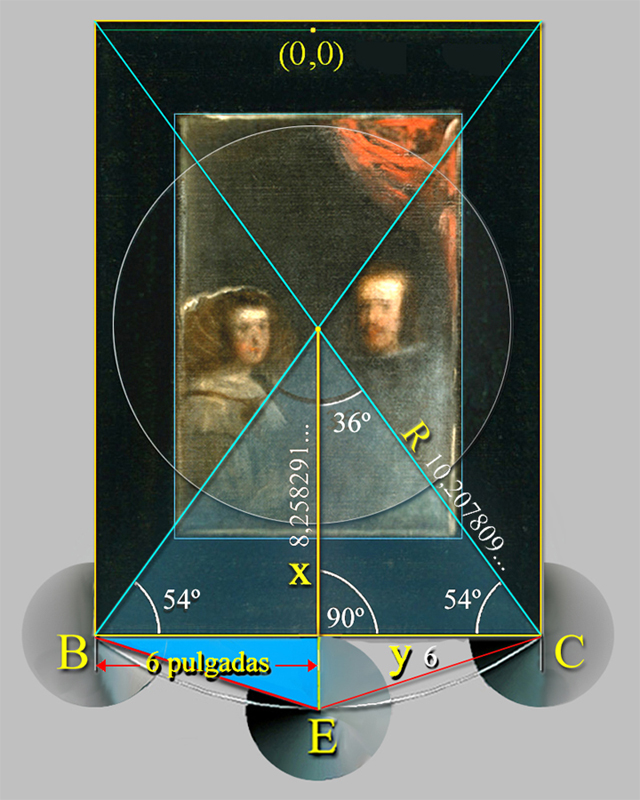 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| 2R |
DIÁMETRO DEL PENTÁGONO |
= | 2 × 10,207809... pulgadas | ≈ | 20,415618... pulgadas | ≈ | 12 Φ + 1 |
2R ≈ 20,415618... pulgadas
12 Φ +1 ≈ 20,416407... pulgadas
|
TOLERANCIA |
0,000888638 unidades | ≈ | 0,0007899 pulgadas | ≈ | 0,018365175 milímetros |
EL ESPEJO & LA GEOMETRÍA SAGRADA
|
Diámetro del Pentágono:
Diámetro del Espejo:
Diagonal Pitagórica:
La expresión 12 Φ + 1:
|
Estos cuatro resultados tienen una tolerancia común, imperceptible al ojo humano, de un tercio de milímetro.
| Elemento | Fórmula | p |
pulgadas | milímetros | |||
| Diagonal Pitagórica | √(16,533223...² + 12²) | ≈ | 20,429172... | 0 | 0 | ||
| Expresión Phi | 12 Φ + 1 | ≈ | 20,416407... | - 0,012765... | - 0,296786... | ||
| Diámetro del Espejo | 12 / sin(π/5) | ≈ | 20,415849... | - 0,013323... | - 0,309759... | ||
| Diámetro del Pentágono | 2 × R | ≈ | 20,415618... | - 0,013554... | - 0,315130... | ||
| Diagonal Phi |
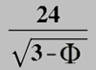 |
≈ | 20,415618... | - 0,013554... | - 0,315130... |
|
|
Estos resultados reflejan una exactitud extrema propia de la ingeniería o la óptica, que en la práctica de la pintura no se requiere, ya que hablamos de una pintura al óleo elaborada con un pincel.
Y aunque esta precisión tiene el propósito lógico de asegurar el dibujo, sin embargo, también funciona como sustento invisible de la perfecta matemática en esta obra de Velázquez, revelando, pues, una intencionalidad indetectable a un nivel de medición convencional, como es el ejemplo del Espejo de Las Meninas, que se convierte en un portal de distintos códigos que unifica la geometría sagrada, la proporción áurea y a la Kabala con la monarquía, otorgando legitimidad y poder divino a la corona española.
 |
|
|
En los próximos renglones analizaremos la anchura del Marco y Cristal del Espejo en relación con su distancia sobre la pared del fondo, y, como mostramos, la anchura real del Marco del Espejo equivale a 45 pulgadas; siendo en este punto donde nos percataremos de la relación directa entre los cuadraditos de la cuadrícula de trabajo y la anchura real del Marco del Espejo:
4,5 cuadraditos miden la anchura del Marco del Espejo y equivalen a 45 pulgadas.
Comprobaremos esta idea con el siguiente ejemplo:
Si 24 cuadraditos de tres unidades de lado componen el ancho de la pared del fondo de Las Meninas, entonces el tamaño real de la pared del fondo medirá 240 pulgadas, como así lo es.
|
Si a 240 pulgadas le corresponden ------------------- 24 cuadraditos a 45 pulgadas le corresponderán ----------------------- X cuadraditos
X = 45 x 24 / 240 = 4,5 cuadraditos. |
El pintor Diego Velázquez midió la anchura real del Marco del Espejo, que medía 45 pulgadas de ancho, y dividió esta cantidad entre 3,333333... pulgadas por unidad.
Comprobemos en el siguiente ejemplo el modo de transportar la medida real de la anchura del espejo sobre el velo o cuadrícula:
45 pulgadas / 3,333333... pulgadas por unidad = 13,5 unidades.
Y se demuestra, pues, que el pintor obtuvo de manera directa la medida proporcional de la anchura del Marco del Espejo, ya que 1 Pie Real equivale en el velo, o cuadrícula de trabajo, a 13,5 unidades.
Este razonamiento matemático plantea una gran lección velazqueña, y demuestra; que la cantidad de 13,5 unidades representó para el artista su medida patrón en todo el proceso creativo de su labor.
La evidencia de una constante matemática permite indagar más en este muro lejano, y conocer con detalle la anchura real del marco de madera del Espejo.
Como debemos saber el marco de madera del espejo mide 13,5 x 18,6 unidades.
|
|
Las medidas del Marco del Espejo |
Si la anchura de la copia de Mazo mide 2,232 metros, que se representa por medio de 28,8 unidades, la anchura real del marco del espejo medirá, exactamente, la cantidad a averiguar:
2,232 metros ------- 28.8 unidades
X --------------------- 13,5 unidades
X = 2,232 x 13,5/28.8 = 1,04625 metros, que es lo que mide la anchura real del marco de madera del espejo.
Traduciendo 1,04625 metros en el sistema castellano tendremos:
1,04625 metros / 0,02325 metros por pulgada = 45 pulgadas = 3 pies y 3/4 de pie, que es lo mismo a 1 vara y 1 palmo.
Y para que redondeemos más esta cantidad; 45 pulgadas también equivalen a 5 palmos, ya que el palmo castellano equivale a 9 pulgadas.
Otro tanto obtendremos si operamos con la altura Y del marco del espejo en este sistema de medición:
2,232 metros ------- 28.8 unidades
Y --------------------- 18,6 unidades
Y = 2,232 x 18,6/28.8 = 1,4415 metros, que es lo que mide la altura real del marco de madera del espejo.
Traduciendo 1,4415 metros en el sistema castellano tendremos:
1,4415 metros / 0,02325 metros por pulgada = 62 pulgadas = 5 pies y 2 pulgadas, que es lo mismo a 1 vara, 2 pies y 2 pulgadas.
Rescatar del olvido un
antiguo sistema de medición castellana, y medir apropiadamente todo el área y perímetro de
Las Meninas ha sido una larga y ardua labor.
Las herramientas adecuadas y el tiempo de estudio necesario han sido la clave del perfeccionamiento de un método aritmético y geométrico exacto.
La anchura del Marco del Espejo mide 13,5 unidades
Factorización de 3 x 3 x 3 x 5 = 135.
Los divisores del número 135 son 8:
1, 3, 5, 9, 15, 27, 45, 135.
135 ÷ 1,125 = 120; que es lo que mide en pulgadas el ancho original del lienzo de Las Meninas.
La altura del Marco del Espejo mide 18,6 unidades
Factorización de 2 x 3 x 31 = 186.
Los divisores del número 186 son 8:
1, 2, 3, 6, 31, 62, 93, 186.
186 ÷ 8 = 23,25; que es la cantidad que equivale en milímetros a una pulgada castellana.
| LA ALTURA | FUNDAMENTO | LA ANCHURA | ||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 0,3844 | 16 y 8/15 | 18,6 | = | 18,6 x 1 | 13,5 x 1 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 9,3 x 2 | 4,5 x 3 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 6,2 x 3 | 2,7 x 5 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 3,1 x 6 | 1,5 x 9 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,6 x 31 | 0,9 x 15 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,3 x 62 | 0,5 x 27 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,2 x 93 | 0,3 x 45 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,1 x 186 | 0,1 x 135 | = | 13,5 | 12 | 0,279 | |
|
|
| Marco del Espejo | Metros | Pulgadas | Unidades | Unidades por pulgada | Pulgadas reales | ||
| Anchura | 0,279 | 12 | 13,5 | = | 0,3 | x | 45 |
| Altura | 0,3844 | 16 y 8/15 | 18,6 | = | 0,3 | x | 62 |
|
|
Respecto
al Cristal del Espejo
analizaremos también su
tamaño real, es decir; su tamaño original antes de que fuera reducido
proporcionalmente de formato y pintado en la pared del
fondo de esta pintura.
Ofrecemos tanto las dimensiones en unidades, pulgadas y metros, sobre la rejilla de trabajo, como la medidas reales en pulgadas de este objeto pintado en Las Meninas en particular:
 |
Las medidas de luces del Cristal del Espejo |
La anchura del Cristal del Espejo mide 8,4 unidades
Factorización de 2 x 2 x 3 x 7 = 84.
Los divisores del número 84 son 12:
1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84.
La altura del Cristal del Espejo mide 12,6 unidades
Factorización de 2 x 3 x 3 x 7 = 126.
Los divisores del número 126 son 12:
1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.
| LA ALTURA | FUNDAMENTO | LA ANCHURA | ||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 0,2604 | 11,2 | 12,6 | 1 x 12,6 | 1 x 8,4 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 2 x 6,3 | 2 x 4,2 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 3 x 4,2 | 3 x 2,8 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 6 x 2,1 | 4 x 2,1 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 7 x 1,8 | 6 x 1,4 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 9 x 1,4 | 7 x 1,2 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 14 x 0,9 | 12 x 0,7 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 18 x 0,7 | 14 x 0,6 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 21 x 0,6 | 21 x 0,4 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 42 x 0,3 | 28 x 0,3 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 63 x 0,2 | 42 x 0,2 | 8,4 | 7 y 7/15 | 0,1736 | |||
| 0,2604 | 11,2 | 12,6 | 126 x 0,1 | 84 x 0,1 | 8,4 | 7 y 7/15 | 0,1736 | |||
|
|
| Cristal del Espejo | Metros | Pulgadas | Unidades | Unidades por pulgada | Tamaño real en pulgadas | ||
| Anchura | 0,1736 | 7 y 7/15 | 8,4 | = | 0,3 | x | 28 |
| Altura | 0,2604 | 12,6 | 12,6 | = | 0,3 | x | 42 |
|
|
Segunda conclusión:
Estos datos confirman, pues, que existe un coeficiente o ratio que pone de acuerdo a la realidad con el tamaño de los elementos u objetos pintados en una lejanía determinada, y que, como dijimos en líneas anteriores, se hallen localizados sólo en la sección geométrica del área del muro del fondo de Las Meninas.
Cualquier resultado calculado en unidades sobre la cuadrícula de medición, al multiplicarlo por 3,333333... pulgadas por unidad, proporcionará, directamente, el valor de la medida real del objeto en estudio localizado sobre esta pared [8].
Veamos un ejemplo:
Si ya sabemos, de antemano, que la cuadrícula de medición la anchura del marco de madera del espejo mide 13,5 unidades, entonces, sólo habrá que multiplicar esta misma cantidad de unidades por el coeficiente mencionado, 3,333333... pulgadas por unidad, para averiguar, sin más, el resultado de las medidas reales en pulgadas de este objeto en particular:
13,5 x 3,333333... = 44,999999... pulgadas.
Y siendo en verdad Las Meninas una pintura valorada por su buena ejecución técnica, corroboraremos, pues, cómo funciona la Geometría de la pared del fondo pintada en este óleo respecto al tamaño real de la Habitación del Príncipe, por lo que utilizaremos en este análisis el teorema de Pitágoras, más el cálculo de las medidas de los lados de los triángulos semejantes de la Geometría de Euclides.
CÁLCULO DEL ANCHO DE LA HABITACIÓN DEL PRÍNCIPE
|
|
60 / 18 = 240 / 72 = 200 / 60 = 10 / 3 = 3,333333... pulgadas por unidad
Esta proporción incluye la escuadra perfecta de Pitágoras
|
|
|
Bertrand Russell en su libro Historia de la Filosofía recomienda [9]:
|
Habitualmente, una hipótesis es un preliminar necesario para la colección de hechos, puesto que la selección de éstos requiere algo previo que determine su importancia. |
|
|
El formato de la pared del fondo de Las Meninas trata, pues, de una proporción sesquiquinta, que es aquella que contiene la unidad y un quinto de ella:
|
5/5 + 1/5 = 6/5
1 + 1/5 = 1,2 |
Basándonos en esta nueva pauta acotaremos a la pared del fondo con medidas reales.
 |
|
|
El tamaño real en pulgadas de las anchuras de los dos vanos de las puertas serían las siguientes:
Vano puerta izquierda: 12 unidades - Quedaría; 12 x 3,333333... = 40 pulgadas.
Vano puerta derecha: 13,5 unidades - Quedaría; 13,5 x 3,333333... = 45 pulgadas.
Las únicas medidas que no se pueden acotar debidamente son las anchuras de los dos pequeños cuadros a ambos lados de la pared, y es a causa de que se pintaron medio velados; aunque calculamos un tamaño de 17 x 40 pulgadas reales para cada uno.
Como dijimos en líneas anteriores:
|
Todo se reduce, una vez calculado en unidades la dimensión del objeto sobre la cuadrícula de trabajo, a multiplicar el resultado obtenido por 3,333333... |
Efectivamente, Diego Velázquez operó de manera inversa:
|
La medida del objeto realizada en pulgadas por el pintor fue dividida por el coeficiente de 3,333333..., y la cantidad obtenida de esta simple operación matemática la transportó sobre la cuadrícula de trabajo en unidades. |
El pintor ante la profundidad.
Acerca de la distancia entre el primer plano y la pared del fondo se puede entender que hay dos tipos de distancias;
una sería la que tenía el tamaño real de la Habitación del Príncipe,
y, la otra, la que interpreta y pinta Velázquez en su óleo.
Estudio de la profundidad de la sala de la esquina suroeste de la planta baja del Alcázar.
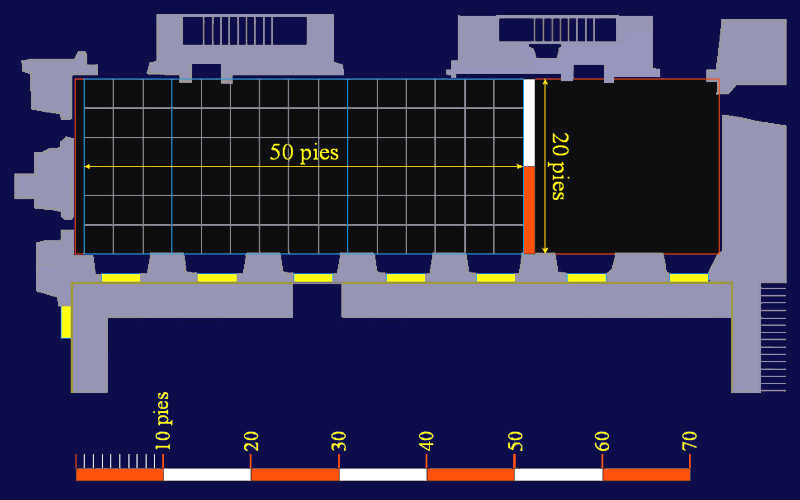 |
|
|
|
El arquitecto del rey Juan Gómez de Mora armonizó las primitivas construcciones que integraban el Alcázar madrileño mediante una larga fachada flanqueada por torreones, es decir; él fue quien hizo el plano de Palacio que aquí estudiamos.
Y en conclusión, el ancho del lienzo de Las Meninas equivale a la mitad de la anchura de esta sala, y la anchura de la pared pintada corresponde a 1/3,75 de esta misma sala.
Escala de la anchura de la sala donde se pintan Las Meninas
La anchura ideal de Las Meninas es de 120 pulgadas, que equivale a 2,79 metros.
Luego la anchura de esta sala será de 2,79 metros x 2 = 5,58 metros = 20 pies = 240 pulgadas.
La dimensión transversal de la distante pared pintada es de 1,488 metros = 64 pulgadas.
La relación entre el tamaño de como se pinta la pared del fondo y su tamaño real: 1,488/5,58 = 0,266666...
Luego la escala de representación de la pared del fondo es de: 1/3,75 = 0,266666...
Es indudable que Velázquez afrontó el lienzo de Las Meninas con la más adecuada Geometría, Aritmética y Matemática; considerando en esta investigación, además, la suma de otras ciencias vedadas en la época del pintor español.
Ante este Muro se estableció una relación de dependencia, por la que el más fuerte, el rey Felipe IV, daba protección y ennoblecía al más débil, Diego Velázquez, a cambio de comprometerse a guardar fidelidad y ejecutar, de manera segura, un trabajo cabalístico.
| LA ALTURA |
LA ANCHURA |
|||||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
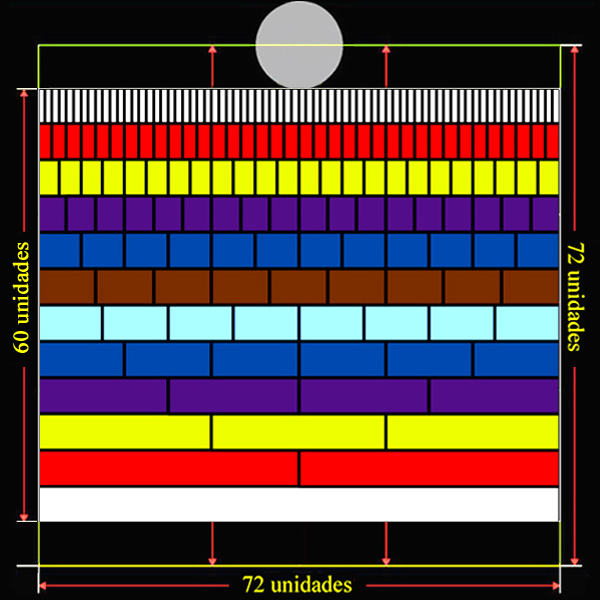 |
Cuadrícula | Unidades | Pulgadas | Metros | ||||
| 1,24 | 53,333 | 60 | = | 72 x 0,833 | 72 x 1 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 36 x 1,666 | 36 x 2 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 24 x 2,5 | 24 x 3 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 18 x 3,333 | 18 x 4 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 12 x 5 | 12 x 6 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 9 x 6,666 | 9 x 8 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 8 x 7,5 | 8 x 9 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 6 x 10 | 6 x 12 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 4 x 15 | 4 x 18 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 3 x 20 | 3 x 24 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 2 x 30 | 2 x 36 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 1 x 60 | 1 x 72 | = | 72 | 64 | 1.488 | |||
|
|
Ratio de la pared del fondo
72 unidades ÷ 60 unidades = 1,2
|
En consonancia con la profundidad de Las Meninas, el tamaño de los distintos elementos pintados en la pared del fondo se miden en la rejilla de trabajo dividiendo la pulgada Castellana en 15 partes iguales. |
| 45 partes | Unidades | La Pulgada en 15 partes | Pulgadas | Milímetros | Pulgadas reales | ||
| 45/40 | = | 1,125 | 15/15 | = | 1 | 23,25 | 3,75 |
| 42/40 | = | 1,05 | 14/15 | = | 0,933333 | 21,7 | 3,5 |
| 39/40 | = | 0,975 | 13/15 | = | 0,866666 | 20,15 | 3,25 |
| 36/40 | = | 0,9 | 12/15 | = | 0,8 | 18,6 | 3 |
| 33/40 | = | 0,825 | 11/15 | = | 0,733333 | 17,05 | 2,75 |
| 30/40 | = | 0,75 | 10/15 | = | 0,666666 | 15,5 | 2,5 |
| 27/40 | = | 0,675 | 9/15 | = | 0,6 | 13,95 | 2,25 |
| 24/40 | = | 0,6 | 8/15 | = | 0,533333 | 12,4 | 2 |
| 21/40 | = | 0,525 | 7/15 | = | 0,466666 | 10,85 | 1,75 |
| 18/40 | = | 0,45 | 6/15 | = | 0,4 | 9,3 | 1,5 |
| 15/40 | = | 0,375 | 5/15 | = | 0,333333 | 7,75 | 1,25 |
| 12/40 | = | 0,3 | 4/15 | = | 0,266666 | 6,2 | 1 |
| 9/40 | = | 0,225 | 3/15 | = | 0,2 | 4,65 | 0,75 |
| 6/40 | = | 0,15 | 2/15 | = | 0,133333 | 3,1 | 0,5 |
| 3/40 | = | 0,075 | 1/15 | = | 0,066666 | 1,55 | 0,25 |
|
|
| Unidades |
Fracción de la pulgada |
Pulgadas |
Milímetros |
Operación |
Tamaño real |
|
| 1,125 |
15/15 |
1 |
23,25 |
1,125
unidades x 3,333333... pulgadas por unidad |
= | 3,75
pulgadas |
| 0,075 |
1/15 |
0,066666... |
1,55 |
0,075 unidades x
3,333333... pulgadas por unidad |
= | 0,25 de pulgada |
|
|
La altura real de la pared del fondo equivaldría a:
60 unidades x 3,333333... pulgadas por unidad = 200 pulgadas.
Es decir; 200 pulgadas x 0,02325 metros por pulgada = 4,65 metros.
 |
|
|
Aclaramos en este renglón que la altura de la pared del fondo es también deudora de su Geometría; lo cual implica que no sólo aportamos la altura real, sino que, además, su altura proporcionada:
60 unidades / 8 = 7,5 unidades.
Entendiendo que la altura de la pared del fondo se haya dividida en ocho partes iguales, surge de la exactitud una referencia concluyente al multiplicar 7,5 unidades por 8 que es igual a 60 unidades, y esta cifra, a su vez, por 3,333333... pulgadas por unidad.
Como se puede comprobar, el resultado son 200 pulgadas reales.
|
|
|
|
|
|
unidades |
pulgadas |
medidas castellanas |
metros |
|
Altura |
225 |
200 |
200 / 12 = 16 pies y 2/3 |
4,65 |
|
Anchura |
270 |
240 |
240 / 12 = 20 pies |
5,58 |
|
|
Teniendo en cuenta que 64 + 24 = 88, se observa, pues, en esta imagen de la medición perimetral de la Habitación del príncipe la utilización sistemática del número 44, que viene a ser, pues, 22 x 2, cuya cantidad en pulgadas completa diez veces la suma de la altura y anchura real de esta sala.
44 + 44 + 44 + 44 + 44 + 44 + 44 + 44 + 44 + 44 = 240 + 200
22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 + 22 = 240 + 200
Acompañaremos esta deducción con lo que se indica en el Sefer Yetzirah 2:4:
|
עשרים ושתים אותיות יסוד קבען בגלגל כמין חומה ברל"א שערים
וחוזר הגלגל פנים ואחור
וסימן לדבר אין בטובה למעלה מענג ואין ברעה למטה מנגע |
Sefer Yetzirah - Capítulo 2:4 |
Veintidós letras de fundamento, las fijó en un círculo semejante a un muro en el que había trazadas 231 puertas.
El círculo oscila adelante y atrás.
Un signo lo muestra: No hay nada mejor entre lo bueno que el deleite, y no hay nada peor entre lo malo que la plaga. |
De los renglones anteriores resaltaremos; veintidós letras, la palabra muro y el número 231, que resultan ser tres cuestiones que aquí tratamos;
la cifra exacta de veintidós letras hebreas que equivalen a los 22 cuarterones de la puerta del fondo,
el lugar o muro donde se sitúan,
y 231 posibles combinaciones [10].
El número 231 representa las veces que dos distintas letras hebreas, estando situadas las veintidós letras a una distancia equidistante en la periferia de un círculo, pueden conectarse.
Al tiempo, como eterno nómada, Velázquez lo asocia, pues, con la cadencia de lo cotidiano en la ruta
celeste de arriba, que es puntual con
los avisos de abajo, y los de abajo con los de arriba,
a fin de rememorar la efeméride de cada jornada a lo ancho de la pared del
fondo.
 |
|
|
|
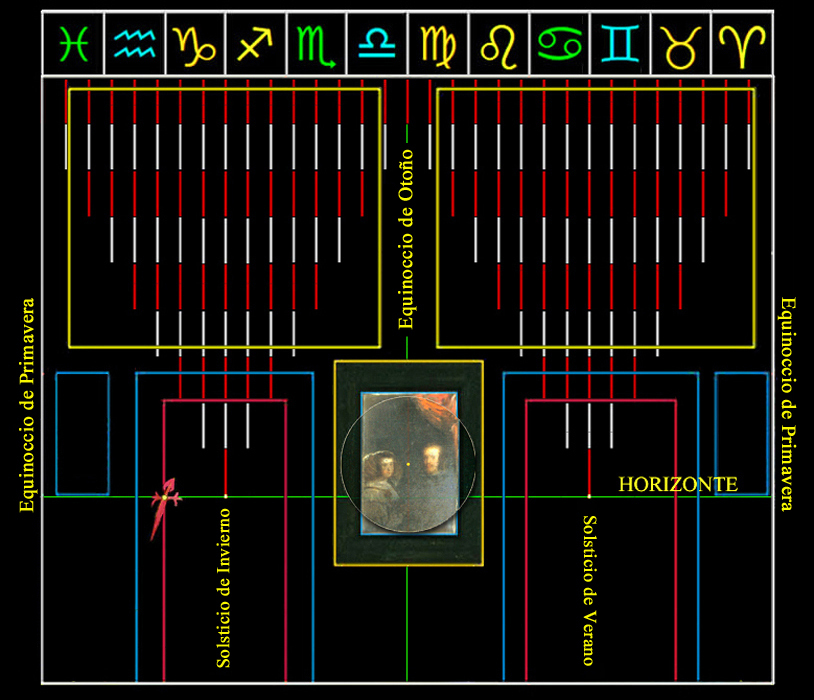
Considerando, pues, que el ancho de la pared del fondo de Las Meninas mide 72 unidades, que representan los 366 días del año bisiesto 1656, podemos mapear los solsticios y equinoccios de la siguiente manera:
|
SIGNO |
ESTACIÓN |
MARCA |
TOLERANCIA |
DÍAS |
INICIO |
|||
 |
Aries |
Equinoccio de Primavera |
0 |
0 |
0 |
20 ó 21 |
Marzo |
|
 |
Cáncer |
Solsticio de Verano |
17,9 |
- 0,1 |
91 |
20 ó 21 |
Junio |
|
 |
Libra |
Equinoccio de Otoño |
36,2 |
+ 0,2 |
184 |
22 ó 23 |
Septiembre |
|
 |
Capricornio |
Solsticio de Invierno |
53,9 |
- 0,1 |
274 |
21 ó 22 |
Diciembre |
|
 |
Aries |
Equinoccio de Primavera |
72 |
0 |
366 |
20 ó 21 |
Marzo |
|
Así pues, una tolerancia de 0,2 unidades en nuestra escala temporal de Las Meninas equivale a 1 día y 24 minutos.
Y de resaltar, la jornada del Apóstol Santiago, día en el que fue bautizada la Infanta por el Nuncio de su Santidad en la Capilla Real, además de la marca del 24 de Junio, San Juan Bautista, sugerida en el suelo del pasillo con pinceladas de luz muy intensa sobre la vertical de la reposada mano izquierda de la Infanta Margarita, lo que hace posible considerar, pues, la consagración de la Infanta como princesa heredera, y, de puertas adentro, reconocida sucesora del trono de Castilla.
 |
|
|
|
En el atrio de la iglesia de Santa María la Mayor, en el municipio de Caspe, Zaragoza, tuvo lugar, el 24 de Junio de 1412, el célebre Compromiso de Caspe, por el cual, a propuesta de los delegados de los parlamentos catalán, valenciano y aragonés, fue otorgada la corona de Aragón a Fernando de Antequera, infante de Castilla. |
Al igual que las manillas del reloj miden el tiempo, mostramos, pues, el tránsito, de derecha a izquierda, de la fugaz línea temporal que da sentido narrativo a esta obra maestra, y, con estricto orden, ilustra la posición de los personajes, objetos o marcas en fechas concretas.
Y ante este tipo de lectura, se desvela gráficamente la salvaguarda de la Infanta:
La marca del cumpleaños de la Infanta, el 12 de Julio,
el día de su santa patrona, el 20 de Julio
y la del patrón del reino de España; Santiago apóstol, el 25 de Julio.
La acotación de los intervalos a lo largo de
la anchura de la pared del fondo lo desarrollamos en la siguiente
ilustración:
 |
|
|
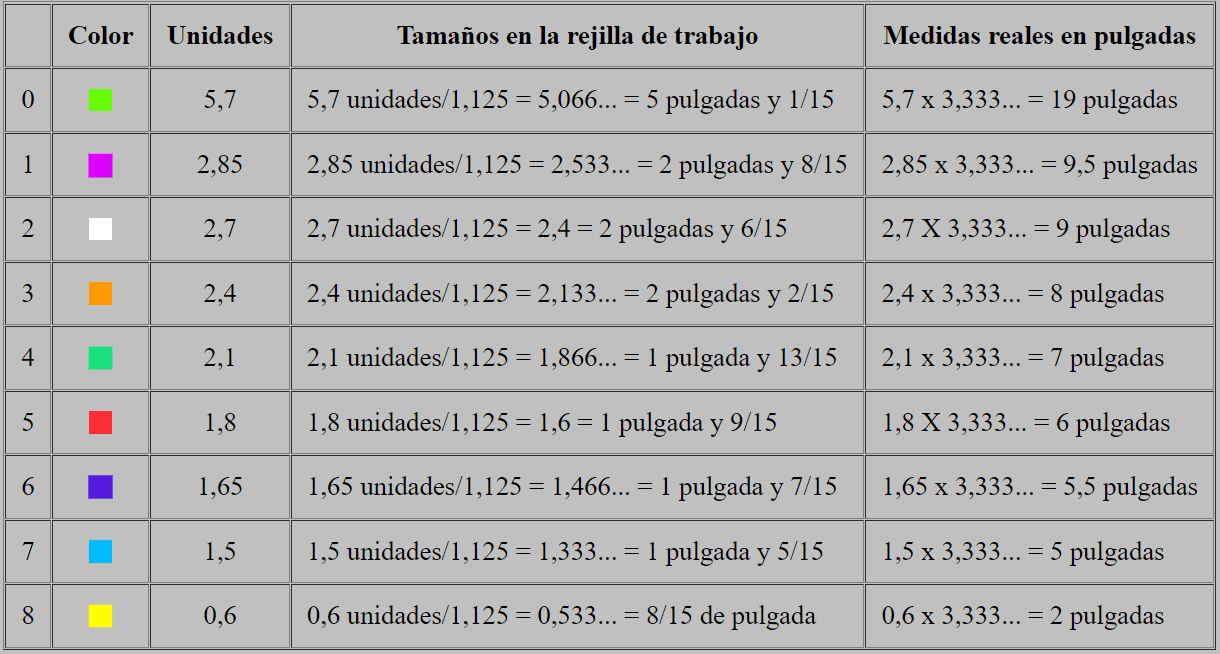
| Desglose | Unidades | Medidas Castellanas en la rejilla de trabajo | Medidas reales en pulgadas |
| Espacio derecho | 1,65 | 1,65 unidades/1,125 = 1,466... = 1 pulgada y 7/15 | 1,65 x 3,333... = 5,5 pulgadas |
| Espacio central izquierdo | 2,55 | 2,55 unidades/1,125 = 2,266... = 2 pulgadas y 4/15 | 2,55 x 3,333... = 8,5 pulgadas |
| Espacio izquierdo | 2,85 | 2,85 unidades/1,125 = 2,533... = 2 pulgadas y 8/15 | 2,85 x 3,333... = 9,5 pulgadas |
| Espacio central derecho | 3,15 | 3,15 unidades/1,125 = 2,8 = 2 pulgadas y 12/15 | 3,15 x 3,333... = 10,5 pulgadas |
| Total | 10,2 | 10,2 unidades/1,125 = 9,066... = 9 pulgadas y 1/15 | 10,2 x 3,333... = 34 pulgadas |
|
|
Ya que es sabido que la perspectiva de esta pared fuga algo hacia su lado izquierdo, pero, como aclaramos ahora, no tratamos este asunto, consideramos estas nuevas medidas en base a la idea de una pared del fondo totalmente frontal, es decir; paralela a los ojos del espectador.
 |
|
|
 |
Para recuperar el tamaño original de los diversos elementos de la pared del fondo hemos operado matemáticamente, ya que hemos desarrollado una innovadora manera de medir distancias, lo más cercano a la realidad, desde el punto de vista del observador.
No obstante, es importante subrayar que los dos grandes lienzo que Velázquez sitúa en la pared del fondo están inspirados en dos tablas de igual tamaño de Peter Paul Rubens, si bien, en el caso de Las Meninas, la alegoría izquierda está estrechada, lo suficiente, para crear un efecto de perspectiva.
 |
Óleos sobre tabla de Peter Paul Rubens - 1637
Dimensiones:
26,7375 x 38,3625 centímetros
11,5 x 16,5 pulgadas |
|
A tomar en consideración
Entre el Horizonte y la Línea de tierra, a lo largo de la parte
baja del ancho
de la pared del fondo, deducimos cuatro cuadrados.
Esta zona en particular mide; 72 unidades de ancho por 18 unidades de alto.
Así mismo, el ancho de la pared del fondo pintada en el lienzo de Las Meninas de 72 unidades dividido entre 4 da como resultado 18 unidades, que es lo que mide el lado de cada uno de estos cuatro cuadrados.
|
|
|
|
Sin forzar mucho la explicación deduciremos a que equivalen 72 unidades:
72 unidades dividido entre 1,125, que es el valor en unidades de una pulgada, es igual a 64 pulgadas.
En definitiva, la perspectiva de Las Meninas interpreta la posición de cada detalle en la distancia tal y como aparece ante nuestra vista siguiendo reglas geométricas consistentes, y es producto de una mente de rigorosa corrección matemática.
Las 72 unidades del ancho de la pared pintada en Las Meninas multiplicadas por el coeficiente 3,333333... pulgadas por unidad es igual a 240 pulgadas, es decir; da como resultado la medida real del ancho de la Habitación del Príncipe.
|
|
|
Localización de la altura del Horizonte de Las Meninas respecto al suelo de la Habitación del Príncipe. |
Aproximándonos hacia el punto X, que trata del punto de fuga de la perspectiva de la Habitación del Príncipe, nos encontramos dependiendo al mismo tiempo del espejo y de la puerta de 22 cuarterones; y esto se debe a que el centro físico de esta pintura se sitúa a medio camino entre estos dos elementos.
Comparemos:
Si la Geometría se defiende con sus números irracionales adecuadamente, por ejemplo con el valor de Pi, 3,14159265358979324..., en la Kabala los números naturales 18, 32, 64 ó 72, son benditos [11].
Veamos cómo se explican:
18 unidades; la altura entre el nivel de ojos y la línea de tierra,
32; las veintidós letras del alefato hebreo más diez Sefirot, sólo hay que sumar los veintidós cuarterones de la puerta semiabierta más las diez esferas que hemos impuesto sobre la superficie de Las Meninas.
64 pulgadas; lo que mide la anchura de la pared del fondo.
72 unidades; el ancho de la pared del fondo.
Este acuerdo numérico suscitado por la Geometría de Las Meninas es imposible inventárselo, y, por supuesto, después de haber perfeccionado un patrón de medidas que garantiza esta afinidad.
La base geométrica de esta investigación se asienta en la perfecta relación entre el antiguo sistema castellano y el
actual sistema métrico.
A continuación analizaremos con detalle este hallazgo.
| Pie Real | cuadraditos | unidades |
| 0,278 metros | 4,5 | 13,5 |
| 0,278635 metros | 4,5 | 13,5 |
| 0,279 metros | 4,5 | 13,5 |
|
|
En el intervalo de un milímetro se halla la diferencia de elegir entre un patrón de medidas u otro.
| Sistema castellano | vara | pie | palmo | pulgada | línea | punto | milímetros | unidades |
| vara | 1 | 3 | 4 | 36 | 432 | 5184 | 837 | 40,5 |
| pie | 1 | 3/4 | 12 | 144 | 1728 | 279 | 13,5 | |
| palmo | 1 | 9 | 108 | 1296 | 209,25 | 10,125 | ||
| pulgada | 1 | 12 | 144 | 23,25 | 1,125 | |||
| línea | 1 | 12 | 1,9375 | 0,09375 | ||||
| punto | 1 | 0,16145833 | 0,0078125 |
|
|
Estudio de la cuadrícula de medición
Si una pulgada equivale a 1,125 unidades en la cuadrícula de trabajo, entonces; sólo hay que multiplicar 1,125 unidades por 12 para obtener 13,5 unidades, que es la cantidad que representa en esta misma cuadrícula 4,5 cuadraditos valiendo el Pie Real 12 pulgadas.
 |
|
|
Un Pie Real igual a 0,279 metros escala las medidas geométricas longitudinales y proporcionales con una equivalencia métrica exacta; por lo que la rejilla de 50 cuadraditos, denominada Límite de la rejilla de 150 unidades, equivale a 133 pulgadas y 1/3:
150 unidades / 1,125 unidades por pulgada = 133,333333... pulgadas.
No obstante, desglosando esta cantidad obtendríamos: 3 varas, 2 pies, 1 pulgada y 4 líneas:
| Sistema castellano | cantidades | operación | total en unidades | operación | total en pulgadas | operación | total en metros | ||||||
| varas | 3 | 3 x 40,5 | = | 121,5 | 3 x 3 x 12 | = | 108 | 3 x 3 x 0,279 | = | 2,511 | |||
| pies | 2 | 2 x 13,5 | = | 27 | 2 x 12 | = | 24 | 2 x 0,279 | = | 0,558 | |||
| pulgadas | 1 | 1 x 1,125 | = | 1,125 | 1 x 1 | = | 1 | 1 x 0,279/12 | = | 0,02325 | |||
| líneas | 4 | 4 x 0,09375 | = | 0,375 | 4 x 1/12 | = | 0,333333... | 4 x 0,279/12/12 | = | 0,00775 | |||
| 150 | 133,333333... | 3,10 |
|
|
Cierto, ésto es lo que mide el lado de la cuadrícula denominada Límite de la rejilla de 150 unidades, y, puntualizaremos un poco más, un cuadradito de 3 unidades de lado en esta cuadrícula equivale a 2/9 de Pie, que es igual, al mismo tiempo, a 2 pulgadas y 8 líneas.
Deduciremos lo que mide un cuadradito de 3 unidades en metros fácilmente porque ya estamos al tanto, que eligiendo un Pie Real igual a 0,279 metros, el lado de esta rejilla cuadrada mide 3,10 metros.
Esta gran cuadrícula cuadrada está constituida por 50 cuadraditos de lado, por tanto; si dividimos 3,10 metros entre 50 obtendremos el resultado de 0,062 metros, que es lo que mide realmente el lado de cada uno de estos pequeños cuadraditos que usamos para medir a Las Meninas.
Cuando decimos que un cuadradito de 3 unidades de lado equivale a 2/9 de Pie estamos dividiendo 0,279 metros entre 9 y multiplicando este cociente por 2, esto da como resultado también 0,062 metros.
Cuando decimos que un cuadradito de 3 unidades de lado equivale a 2 pulgadas y 8 líneas, primero dividimos 0,279 metros entre 12, que da como resultado 0,02325 metros, y a esta cifra la multiplicamos por 2; que es igual a 0,0465 metros o 2 pulgadas.
Por otro lado, una línea es el resultado de dividir 0,02325 metros, el equivalente de una pulgada, entre 12 que es igual a 0,0019375 metros; pero hemos dicho 8 líneas, por lo tanto multiplicamos ahora por 8 esta última cantidad y obtendremos este nuevo resultado; 0,0155 metros.
Sólo habrá que sumar 0,0465 metros más 0,0155 metros para obtener 0,062 metros que es el resultado que buscábamos.
notas a pie de página
1 - Apolo vencedor de Pan.
La historia del extraño concurso se inspira en fuentes clásicas.
El monte Tmolo corona de laurel a Apolo, mientras que el sátiro Pan y el rey Midas esperan sentados.
Pan se jacta de tocar mejor su flauta que Apolo su lira, pero en el concurso gana el hijo de Júpiter. Midas protesta y es castigado:
 Le Trasformationi Di M. Lodovico Dolce - Publius Ovidius Naso. Venecia. MDLVIII. |
Do mientras Pan tocaua enternecido La liſa y encerada cañavera, A las ſagradas Nimphas preſentando Sus verſos amoroſos, de manera De ſu harmonia, y voz ſe fue pagando, Que tiene en poco a Apolo, y deſafia Al miſmo, por juez Tmolo eſtando, Sentado el viejo Tmolo ya ſe auia Sobre ſu miſmo monte, y del oydo Los ramos de los arboles deſuia. De robre coronado proueydo De verdes abellotas, que alas ſienes Colgauan, y en vn punto conuertido Al Dios de los ganados. Aqui tienes Iuez aparejado (dixo) atento A tu cantar, no reſta mas que ſuenes. Con ſus agreſte canas al momento Sono el Dios Pan, y el barbaro ſonido Al mas que tonto Midas dio contento, Que a caſo a tal ſazon auia venido. Comiença el ſacro Apolo (y al inſtante A eſſe ha el cano Monte conuertido) Al qual fue ſu arboleda ſemejante. Del arbol de Parnaſo coronado El cabello dorado rutilante, Y vna ropa muy rica atauiado |
De puriſsima grana que barria El ſuelo donde Phebo eſta parado. Con ſu vihuela de arco que trahia En la ſinieſtra mano de ſino oro, Y marfil liſo, y rica pedreria. En la derecha el plectro, tal decoro Fue el del maeſtro, muſico excelente, Por tal tenido en el diuino coro. Y començo a tañer tan dulcemente Que Tmolo de ſu canto comouido, Iuzgo por el, y dixo lo que ſiente A Pan, que le ternien por comedido, Si la zampoña ruſtica y ſu verſo Vuieſſe a la vihuela ſometido. El juyzio del monte no es diuerſo Del que tenian todos, pues conſiente Con ſu ſentencia todo el vniuerso. Injuſta la llamaua ſolamente El inſenſato Midas, y procura Apolo quel caſtigo ſea decente. Perdieron ſus orejas la figura De humanas, y creſcieron de manera, Que ſon orejas de aſno en ſu hechura. El vello por de dentro blanco era Inſtables ſon, y puede a ſu contento Moverlas, lo qual antes no pudiera. En lo demas es hombre, que el intento |
Fragmento del Libro XI de la Metamorfosis de Ovidio. Página 119 del libro de las Transformaciones de Ouidio del Licenciado Pedro Sánchez de Viana - Año 1589.
2 - Análisis de la anchura de las copias de los dos cuadros de Mazo en la pared del fondo de Las Meninas.
Conocemos vagamente las medidas de estos cuadros gracias al Inventario de 1686 del Alcázar.
Leemos:
|
Pieza principal (del cuarto bajo llamado del Príncipe)
(889)
(890)
|
Hoy en día sólo podemos contrastar con el Inventario de 1686 la anchura de la pintura situada en la parte superior derecha de la pared del fondo de Las Meninas.
Esta operación matemática representa el ancho real de esta pintura: 96 pulgadas x 0,02325 metros por pulgada = 2,232 metros, es decir; 8 pies, que equivalen a 2 varas y 24 pulgadas; que corresponden a la anchura verdadera que ofrece actualmente el Catálogo del Museo del Prado.
La anchura que aporta el Inventario, de dos varas y media, resulta ser algo más estrecha que la realidad.
dos varas y media = 36 pulgadas + 36 pulgadas + 18 pulgadas = 90 pulgadas.
Es decir; la anchura real de esta pintura del Museo del Prado es más ancha que la que ofrece el Inventario de 1686, exactamente 6 pulgadas.
CORPUS VELAZQUEÑO - Documentos y Textos - Tomo II. Secretaría General Técnica. Dirección de Bellas Artes y Bienes Culturales. Madrid 2000.
3 - En el año 1567, y tras el fracaso del Ordenamiento de Montalvo iniciado por los Reyes Católicos en 1484, Felipe II promulga el Código conocido como Nueva Recopilación de las Leyes de España, mediante el cual intenta acabar con el caos legislativo existente.
Dentro de este Código recopilado por las Cortes de Valladolid y Madrid a partir de 1523; de las Leyes del Fuero Real, las 18 Leyes de Toro, el Ordenamiento de Alcántara y el de Montalvo, se enmarca la pragmática dictada por el propio monarca desde El Escorial el 24 de junio de 1568:
Y otroſi, que el paño y lienço y ſayal, y las otras coſas que ſe venden a varas, que ſe vendan por la vara Caſtellana: y en cada vara, que den una pulgada al traues, y que se midan el paño por eſquina: y declaramos que la vara Caſtellana de que ſe ha de vſar en todos eſtos Reynos, ſea la que hay y tiene la ciudad de Burgos.
Libro quinto - Titulo XIII. RECOPILACION de las Leyes deſtos Reynos, hecha por mandado de la Mageſtad Catholica del Rey don Philippe Segundo nuestro Señor. Alcala de Henares, en casa de Iuan Iñiguez de Liquerica impreſſor de libros. Año M.D.LXXXI.
4 - Alcázar de Madrid - José Manuel Barbeito - Comisión de Cultura - Colegio Oficial de Arquitectos de Madrid. 1972.
5 - Antonio Palomino de Castro y Velasco, 1653 - 1726, alumno de Valdés Leal y de Juan Alfaro.
Palomino es autor del MUSEO PICTÓRICO Y ESCALA ÓPTICA.
Esta obra está dividida en tres partes: Theorica de la pintura, Práctica de la pintura y el parnaso español pintoresco y laureado.
Deberíamos ser cautos a la hora de pronunciarnos sobre la verdadera ubicación de Las Meninas, pero entendiendo que Palomino muere ocho años antes que el incendio del Alcázar, 24 de Diciembre de 1734, pensamos que es la única autoridad sobre tal asunto.
Palomino, como testigo contemporáneo de los últimos años del viejo Palacio, describe el cuarto donde se pinta esta pintura con estas palabras: En esta galería, que es la del cuarto del Príncipe, donde se finge, y donde se pintó, se ven varias pinturas por las paredes, aunque con poca claridad; conócese ser de Rubens, e historias de los Metamorfosios de Ovidio. Tiene esta galería varias ventanas, que se ven en disminución, que hacen parecer grande la distancia; es la luz izquierda, que entra por ellas, y sólo por las principales, y últimas.
Página 250 de la edición Aguilar, S. A. de Ediciones, 1947, 1988 - Tomo III - El Museo pictórico y escala óptica - El parnaso español pintoresco laureado.
6 - Página 290, final de nota 51. OTRAS MENINAS. Edición a cargo de Fernando Marías. Ediciones Siruela S. A. - Madrid. 1995.
7 - La reconstrucción del lugar denominado Galería del Cuarto Bajo llamado del Príncipe que nos ofrece Moffit, con dibujos elaborados por Terry L. Fox, dan para esta sala de Palacio una anchura exactamente igual a la que tratamos, es decir; 20 pies.
Página 176, John F. Moffit - Anatomía de Las Meninas; realidad, ciencia y arquitectura. Boletín del Museo del Prado. Septiembre-Diciembre 1986.
8 - Como hemos ya desarrollado, la anchura de la pared del fondo equivale a 72 unidades <=> 20 pies Castellanos = 5,58 metros.
Y hemos afirmado, también, que no tenemos la menor duda sobre la anchura exacta del tamaño real de la pared del fondo de Las Meninas.
Sabemos que la anchura de tres varas y tercia, sin marco con bastidor, del Inventario de 1734 equivalen a 120 pulgadas castellanas.
Y que diez pies de ancho, medida anotada en la reproducción de Las Meninas de 1799 por Pierre Audouin , hacen un total de 120 pulgadas.
Tanto en un caso como en el otro 120 pulgadas equivalen a 2,79 metros.
Es decir: 120 pulgadas x 0,02325 metros la pulgada = 2,79 metros.
Lo cual significa que posteriormente a estas fechas se perdieron 3 centímetros de la anchura del lienzo original.
Es decir: 2,79 metros - 2,76 metros = 0,03 metros.
Con la ayuda de estos datos vamos a demostrar la relación de las 72 unidades <=> 20 pies Castellanos = 5,58 metros con la medida en metros de la anchura del lienzo de Las Meninas que nos ofrecen estas mismas fuentes.
72 unidades x 3,333333... pulgadas por unidad = 240 pulgadas = 20 pies Castellanos = 5,58 metros.
Bien; sólo habrá que dividir entre dos: 5,58 metros / 2 = 2,79 metros, y este resultado significa que la anchura total del lienzo de Las Meninas, según el Inventario de 1734, corresponde a la mitad de la anchura exacta de esta pared del Palacio.
 |
Desglose de la anchura actual de Las Meninas
2,761583333 metros = 133,625 unidades; que equivalen a 118 pulgadas y 7/9.
|
Análisis
Por lo tanto: El ancho real de la pared del fondo de 5,58 metros sí está relacionado con la anchura del lienzo de Las Meninas.
Sobre la rejilla de medición 72 unidades / 1,125 unidades por pulgada = 64 pulgadas.
64 pulgadas x 0,02325 metros la pulgada = 1,488 metros, que equivale al tamaño de la anchura de la pared del fondo tal cual fue pintada.
1,488 metros / 2,79 metros = 0,533333...
0,533333..., que es igual a 8/15, representa la escala a la que fue reducida el tamaño de la anchura de la pared del fondo tal cual fue pintada respecto a la anchura total del lienzo de Las Meninas según el Inventario de 1734.
Conclusión
La comparación de los porcentajes nos dan una lectura más abreviada:
Caso primero - Respecto al tamaño de la anchura total del lienzo de Las Meninas según el Inventario de 1734:
2,79 metros -------------- 100 %
1,488 metros -----------53,333333... %
Caso segundo - Respecto la anchura exacta de esta pared del Palacio:
5,58 metros -------------- 100 %
1,488 metros -----------26,666666... %
9 - HISTORIA DE LA FILOSOFÍA. Bertrand Rusell. Traducción: Julio Gómez y Antonio Dorta. RBA Colleccionables S.A. - Barcelona. 2005.
10 - Todo lo que parece sencillo se puede complicar; pero daremos la ayuda necesaria para que esto no ocurra.
|
|
|
n, que es igual a 22, representa la cantidad de elementos, o letras hebreas, que disponemos; y p, que es igual a 2, es el número de elementos, o letras hebreas, que forma cada combinación.
La solución es 231. |
11 - Sefer Yetzirah, El Libro de la Creación. Teoría y Práctica, razonado y explicado por Aryeh Kaplan. Editorial Mirach, S. L., 1994.
Título en inglés: Sefer Yetzirah. The Book of Creation. Publicado por acuerdo con Samuel Weiser, Inc. 1990.
|
La Kabala y Las Meninas |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |