|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fentoni tiene licencia CC BY-NC 4.0 |
|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fentoni tiene licencia CC BY-NC 4.0 |
|
|
El Tetraktys
Escribe Francisco Sanchez, Cathedratico de
Rhetorica de la Vniuerſidad de Salamanca,
en el prólogo del libro séptimo de Arithmetica Practica de Juan Pérez de Moya [1]:
|
De tal manera, curioſo lector, los Pythagoricos reduxeron à numeros todas las coſas, que aun nueſtra anima racional quiſieron que de numeros fueſſe compueſta: & eſtos numeros del anima eran 4 que contados deſde vno hazen diez & perfecto triangulo. Y aſsi el mayor juramento que hazian era por el numero quaternario, de que el anima conſtaua. Lo qual todo aunque pareſce rediculo, no careſce de buen fundamento. Porque en el anima hallauan ellos auer quatro coſas: de las quales toda ſciencia & arte, y los hombres racionales eran conſtituydos.
Eſtas ſon: Entendimiento, Sciencia, Opinion, Sentido.
|
El Tetraktys, Τετρακτύς, simboliza, pues, el anagrama del juramento pitagórico de diez puntos dispuestos en un triángulo equilátero.
1 + 2 + 3 + 4 = 10
|
|
Escribe Heinrich Cornelius Agrippa von Nettesheim - De occulta philosophia libri tres - 1533.
Multam quoq; & maximam in myſteriis uim haber: hinc Pythagorici ipſum quaternarium iureiurando teſtabantur, tanquam ſummum quo fides nitatur & credulitas firmari poſſit: hinc dictum Pythagoricum iuſiurandum, quod in his uerſibus ſic expreſſit:
Por mucho, pues, era el mayor de los misterios, por eso testificaron los pitagóricos, juraban por el mismo cuaternario, como lo más alto en donde descansa la fe para fortalecer la credibilidad, y se decía que era gracias al juramento pitagórico, que se expresa con estas palabras:
|
|
|
Significado del Tetraktys pitagórico:
La Unidad - Lo divino, origen de todas las cosas; el ser inmanifestado.
La Díada - Escisión del punto; origen del principio masculino - femenino.
La Tríada - Los tres niveles del mundo; celeste, terrestre e infernal, y todas las trinidades.
El Cuaternario - Los cuatro elementos; fuego, agua, tierra y aire.
Así pues, el Tetraktys pitagórico es un ideograma de la Geometría que explica diversas cuestiones;
la fuente de la Creación,
la raíz de la eterna Naturaleza,
la armonía de los contrarios,
la esencia numérica de todas las cosas,
el eterno retorno... [2].
|
|
+. Tenebræ abſolutæ. a. Lux prima creatura. b. Prima mixtio lucis cum tenebris. c. Lux. d. Aqua. 2. Tenebræ ſeu ſecundus compoſitionis ſimplicis gradus. e. Ignis. f. Aer. g. e. Aqua. 4. Terra : Radix. 2. Quadratum. 4. Vbi numerus binarius eſt radix materialis, ex qua primun quadratum. 4. elementa indicans deriuatur, ita etiam in corporum perfecte mixtorum productione totidem gradus interſunt, in motu naturæ, à quadrato ſeu 4. elementis, ad cubum ſeu elementarum perfecte miſtum, qui omnes gradus corpora imperfecte miſta reuera ſunt dicenda, vtpote qui à ſimplicitate elementorum mixtionem verſus progrediuntur, progreſſio igitur à quadrato ad cubum eſt huiuſmodi. |
Un buen ejemplo de esta filosofía hermética lo aporta el humanista inglés Roberti Fludd, alias DE FLVCTIBUS, en su libro: Philoſophia ſacra et vere Chriſtiana Seu Meteorologia Cosmica. Francofurti, 1626, en el que establece un concierto entre la parte física del hombre, arraigada a la naturaleza, y la parte anímica e inmortal, unida a Dios.
Y cierto es que existe, además, una congruente conexión entre las 22 + 1 intersecciones de la geometría de la estrella de seis puntas, llamada la Estrella de David, y el triángulo equilátero que compone el Tetraktys pitagórico.
|
Estos son los Diez Sefirot de la nada: El aliento de Dios vivo, aliento del aliento, agua del aliento, fuego del agua. Arriba, abajo, sur, norte, este, oeste.
אלו עשר ספירות בלימה רוח אלהים חיים רוח מרוח מים מרוח אש ממים רום ותחת ודרום צפון מזרח ומערב
Sefer Yetzirah 1:14 |
|
No obstante, se puede confirmar la estrecha relación entre la terna pitagórica: 3 - 4 - 5, y los 22 senderos del Árbol Sagrado de la Vida.
(3) + (3 + 4) + (3 + 4 + 5) = 22
|
|
| 3 | ||||
| 3 | 4 | |||
| 3 | 4 | 5 |
La siguiente triangulación del número 22 alude, también, a las 22 letras hebreas, cada cifra es la suma de las dos que están situadas por encima de ella.
|
|
|
|
|
|
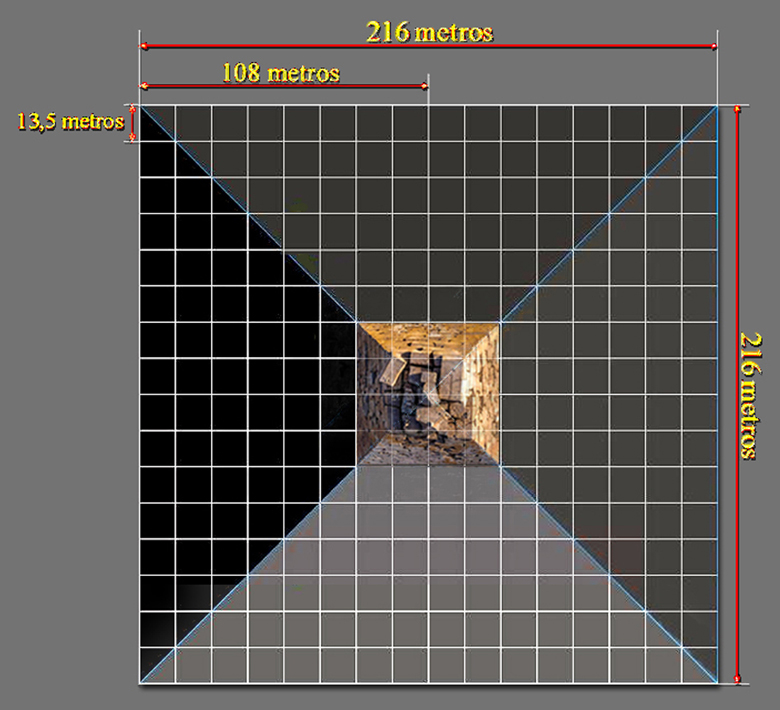
Como se puede comprobar, el número 22, cuyo sumandos son; 1 + 3 + 6 + 12, pertenece al orden pitagórico, al igual que en Egipto los 216 módulos de piedra caliza que conforman la base de la Pirámide de Kefrén hacen, bloque a bloque, una longitud total de 216 metros.
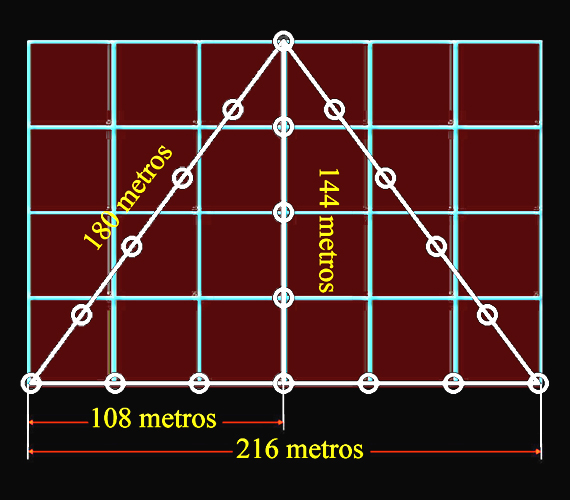 |
Terna pitagórica de la Pirámide de Kefrén en metros |
Y se demuestra, pues, la importancia del número 216, cuya cantidad es igual a lo que mide en metros la base de la Pirámide de Kefrén.
|
Magnitud |
Divisiones | Dedos Egipcios | Milímetros |
|
Vara de Maya |
28/28 |
28 |
525 |
|
Vara Castellana |
36/36 |
44,64 |
837 |
|
Metro |
1000/1000 |
53,333333... |
1000 |
|
|
Convertiremos, pues, los 216 metros de la base de la Pirámide de Kefrén en dedos egipcios:
216 metros x 53,333333... dedos egipcios por metro = 11.520 dedos egipcios.
| 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 |
| 12 | 15 | 16 | 18 | 20 | 24 | 30 | 32 | 36 |
| 40 | 45 | 48 | 60 | 64 | 72 | 80 | 90 | 96 |
| 120 | 128 | 144 | 160 | 180 | 192 | 240 | 256 | 288 |
| 320 | 360 | 384 | 480 | 576 | 640 | 720 | 768 | 960 |
| 1152 | 1280 | 1440 | 1920 | 2304 | 2880 | 3840 | 5760 | 11520 |
|
|
Esta tabla de divisores del número 11.520 representa, razonablemente, las 54 maneras posibles de operar que este guarismo ofrecería a un antiguo constructor egipcio en sus cálculos matemáticos.
 |
|
|
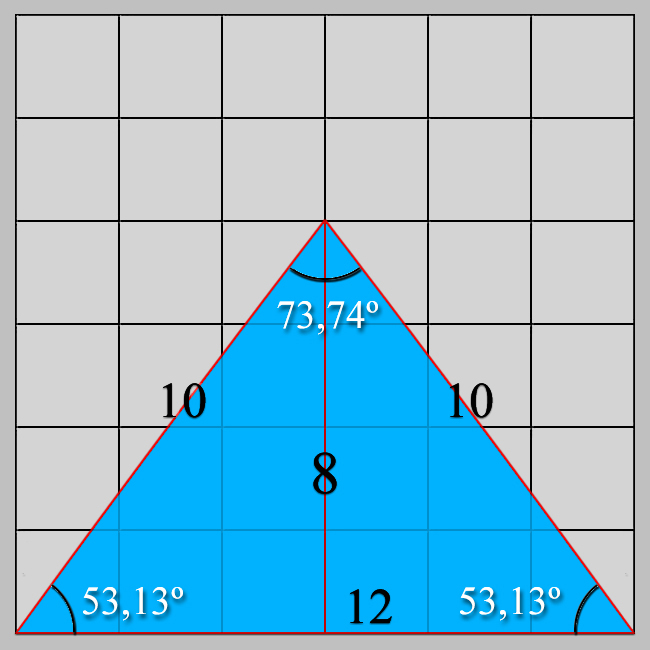
A partir de un múltiplo de 3 se genera el tamaño de una pirámide, cuyo ancho de base en el caso de la Pirámide de Kefrén mide 216 metros, aunque, hoy en día, se consideran las medidas del tamaño de esta pirámide levemente más pequeño.
Geométricamente, son 0,375 x 2 = 0,75 metros de la base los que se echan en falta para poder operar eficazmente.
| 1/2 Base | Altura | Hipotenusa |
| 107,625 metros | 143,5 metros | 179,375 metros |
|
|
|
|
|
1/2 Base |
Altura |
Hipotenusa |
Hablamos, pues, de una Arqueología exacta, por lo que aportaremos más precisión en las medidas de la Pirámide de Kefrén.
Resumiendo; se echan en falta en los datos actuales de las medidas de esta Pirámide, pues, las siguientes cantidades:
| Base | Altura | Hipotenusa |
| 40 dedos egipcios | 26,666666... dedos egipcios | 33,333333... dedos egipcios |
No obstante se confirma, por tanto, que analizamos una construcción geométrica perfecta, y, que, por otro lado, es incierto que la diezmillonésima parte del arco de meridiano, que va del polo Norte al Ecuador, equivalga a un metro centesimal, aunque se implantara en España, por ley del 19 de julio de 1849, como nuevo patrón de medidas longitudinales, sustituyendo al sistema de medidas castellano instaurado por el rey Felipe II en 1568.
La misma vara de 18 metros de longitud del sistema uncial egipcio valdría para rebatir tal criterio científico, y, más recientemente, pues, ya existía un patrón de medida de 100 centímetros de longitud, que, a lo largo de la historia, nadie supo de su existencia, sin embargo, fue el fundamento, por ejemplo, del tamaño del Brazo florentino.
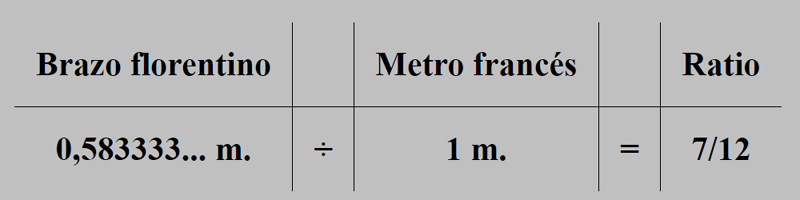
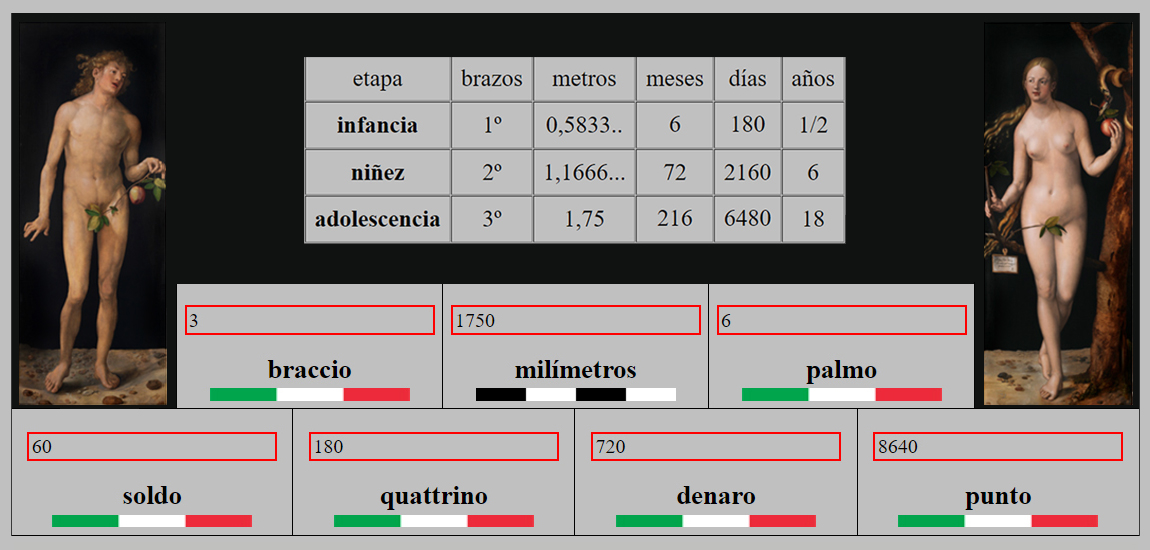
Los sistemas más antiguos de medición están basados, pues, en el tamaño del cuerpo humano, de cuyas proporciones surgió el patrón estándar de medidas antropométricas, y que, con cumplida mejora, se empleó en la ciudad de Florencia ligado al tiempo, ya que, como mostramos en la siguiente tabla, sus cálculos se basaron en el crecimiento del ser humano.
|
|
Pero volvamos a la España del último tercio del siglo XVI, a la época de la construcción del Escorial, y analicemos a continuación el tamaño idóneo del pie castellano.
Veamos:
Si el pie castellano se compone, pues, de 12 pulgadas, y mide 0,279 metros, análogamente, dando a la pulgada castellana el valor 1,125 unidades, un pie de 12 pulgadas equivaldrá, por tanto, a 13,5 unidades.
Y tenemos, que el pie castellano, al no ser divisor del metro francés, sin embargo, su valor absoluto sí está relacionado con las medidas del antiguo Egipto, ya que es parte proporcional de la base de la Pirámide de Kefrén.
216 metros ÷ 13,5 unidades = 16 metros por unidad.
Conclusión:
Los 216 metros de la base de la Pirámide de Kefrén equivalen, pues, a 16 bloques de piedra de 13,5 metros de lado cada uno.
 |
|
|
Sacamos en conclusión dos cuestiones relacionadas;
la primera avalaría la manera de construir en el antiguo Egipto con patrones geométricos de acuerdo con la terna pitagórica,
y que ahora, por primera vez, estamos redefiniendo el origen y longitud del metro según el tamaño pitagórico de 216 metros de la base de la Pirámide de Kefrén.
Y esta trascendencia numérica de los lados del triángulo rectángulo también se tuvo en cuenta en la concepción de los 22 arcanos mayores de las cartas del Tarot, ya que a los máximos dignatarios del poder, terrenal y espiritual, se les asignó los números ordinales de la terna pitagórica:
3 - 4 - 5.
|
|
|
Jean Noblet - Paris. 1650 |
Unos números que el pintor Pellegrino Tibaldi anota en una tablilla situada ante Salomón y la Reina de Saba en el centro de la Biblioteca del Escorial, a la altura del fresco de la Aritmética, donde, además, se hallan sobre una mesa;
una vara de medir,
una balanza
y la sucesión pitagórica, 1, 2, 3 y 4, del Tetraktys.
En este fresco se plasma a Salomón resolviendo los enigmas planteados por la Reina de Saba, no obstante, la legendaria sabiduría que caracterizó a este rey bíblico no deja de ser una característica reveladora del alter ego del rey Prudente Felipe II.
|
|
OMNIA IN NUMERO, PONDERE ET MESURA
TODO TIENE NÚMERO, PESO Y MEDIDA |
|
|
En el lateral del tapete carmín de la mesa está escrita una frase en hebreo que recalca la importancia del sistema de pesos y medidas, y, en particular, sobre la mesa, destaca, pues, la Vara Real de Burgos, que Felipe II en 1568 estandarizó para promover la uniformidad en las medidas utilizadas en la construcción del Monasterio del Escorial y en sus dominios:
Y declaramos que la vara Caſtellana de que se ha de uſar en todos eſtos Reynos, ſea la que hay y tiene la ciudad de Burgos.
GEOMETRÍA DE LA VARA CASTELLANA
|
En el siglo XIX, ante la imposición del metro francés en el sistema de medidas europeo, la Vara castellana sobrevivió gracias a que su tamaño corresponde, pues, a 837 milímetros.
En definitiva, un número de 7 factores:
|
MILÍMETROS |
1 |
3 |
9 |
31 |
93 |
279 |
837 |
|
|
|
|
|
|
|
|
|
|
PULGADAS |
0,0430107... |
0,129032... |
0,387096... |
1,333333... |
4 |
12 |
36 |
|
|
Y consideraremos, además, la aplicación práctica de la teoría musical por el maestro Velázquez en el formato de la Fragua, cuyos sonidos armónicos Pitágoras descubrió en el repicar de unos martillos batiendo un yunque.
 |
 |
|
|
| Autor |
Medidas del Catálogo |
Reajuste |
Sistema castellano |
Ratio |
|
Diego Velázquez |
2,90 x 2,23 metros |
2,976 x 2,232 metros |
128
x 96 pulgadas |
4/3 |
|
|
Según la leyenda, Apolo se enamoró del sonido de la lyra de Hermes, y éste se la regaló como compensación de haberle robado un rebaño de ovejas cuando era un niño, y aunque Apolo no inventara ningún instrumento musical es considerado dios de la Música, y representante de la armonía cósmica de las esferas.
Como arte liberal, la trascendencia numérica; 3 - 4 - 5, del tamaño de los lados del triángulo rectángulo de Pitágoras, va más allá de la Geometría, porque constituye la base armónica de las Matemáticas de la Música.
Y asimismo, en el caso de Las Meninas, estos tres números pitagóricos no sólo estructuran su Geometría, sino que además armonizan la composición.
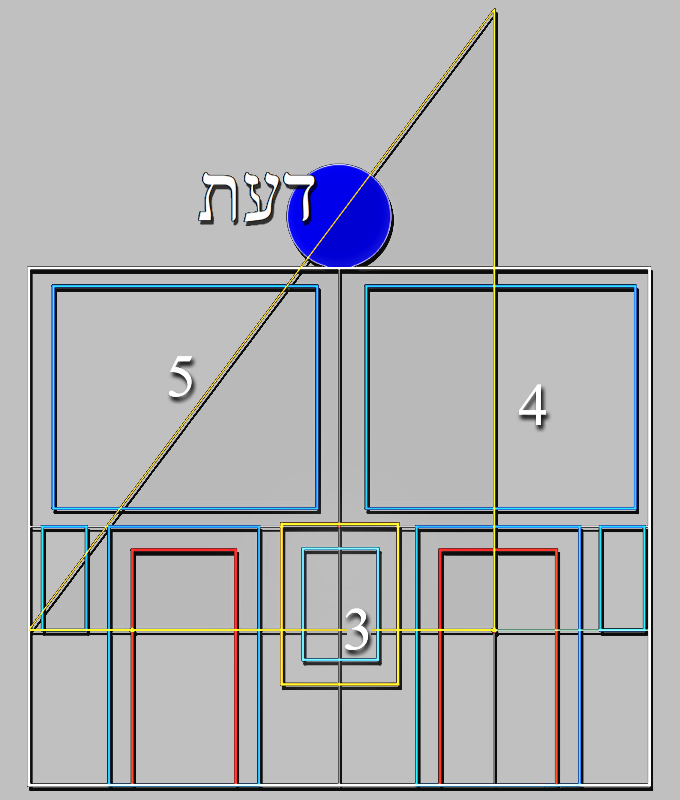 |
|
|
En busca de la unidad
Asevera, pues, el bachiller Iuan Perez de Moya
en su libro ARISMETICA PRACTICA, Y ESPECULATIVA. Año M. DCIX:
El fundamento, o principio de la Ariſmetica, es la vnidad, aſsi como el punto lo es de la Geometria.
Y como hemos ya señalado, los antiguos filósofos pitagóricos comparaban a la unidad, por ser divina, con el entendimiento, mientras que a la Ciencia, fundamentada en el Axioma y en la Doctrina, llamaban dos.
|
En la siguiente tabla se plasma el descubrimiento del valor de la pulgada castellana traducida a unidades; lo cual indica que nos hallamos ante la cuantía de 1,125 unidades por pulgada, o número conversor, que traduce las pulgadas castellanas en cualquier clase de sistema de medidas longitudinales, y que, con exactitud, también nos pone en contacto con las dimensiones reales de Las Meninas. |
1,125 unidades x 0,888.888 pulgadas por unidad = 1 pulgada.
1 pulgada = 0,279 metros / 12 = 0,02325 metros.
| 9 partes | Unidades | La Pulgada en 9 partes | Pulgadas | Milímetros | ||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 |
| 8/8 | = | 1 | 8/9 | = | 0,888888 | 20,666666 |
| 7/8 | = | 0,875 | 7/9 | = | 0,777777 | 18,083333 |
| 6/8 | = | 0,75 | 6/9 | = | 0,666666 | 15,5 |
| 5/8 | = | 0,625 | 5/9 | = | 0,555555 | 12,916666 |
| 4/8 | = | 0,5 | 4/9 | = | 0,444444 | 10,333333 |
| 3/8 | = | 0,375 | 3/9 | = | 0,333333 | 7,75 |
| 2/8 | = | 0,25 | 2/9 | = | 0,222222 | 5,166666 |
| 1/8 | = | 0,125 | 1/9 | = | 0,111111 | 2,583333 |
|
|
|
|
|
|
||||
| UNIDAD | PULGADA | MILÍMETRO |
| Sistema castellano | vara | pie | palmo | pulgada | línea | punto | milímetros | unidades |
| vara | 1 | 3 | 4 | 36 | 432 | 5184 | 837 | 40,5 |
| pie | 1 | 3/4 | 12 | 144 | 1728 | 279 | 13,5 | |
| palmo | 1 | 9 | 108 | 1296 | 209,25 | 10,125 | ||
| pulgada | 1 | 12 | 144 | 23,25 | 1,125 | |||
| línea | 1 | 12 | 1,9375 | 0,09375 | ||||
| punto | 1 | 0,16145833 | 0,0078125 |
|
|
La pulgada dividida en nueve fracciones, que llamamos la división velazqueña, está en estrecha relación con cada una de las 12 líneas en las que se divide la pulgada castellana:
|
A través de las cantidades 3 y 4; números correspondientes al tamaño de los catetos del triángulo pitagórico o escuadra perfecta. |
| la división velazqueña | la pulgada castellana |
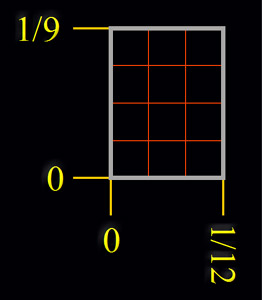 |
| 1/9 = 16 puntos | 1/12 = 12 puntos | |
| 4 partes x 9 = 36 partes | 3 partes x 12 = 36 partes | |
| 9 fracciones | 12 fracciones | |
| 1/9 ⇔ 23,25/9 = 2,583333 milímetros | 1/12 ⇔ 23,25/12 = 1,9375 milímetros |
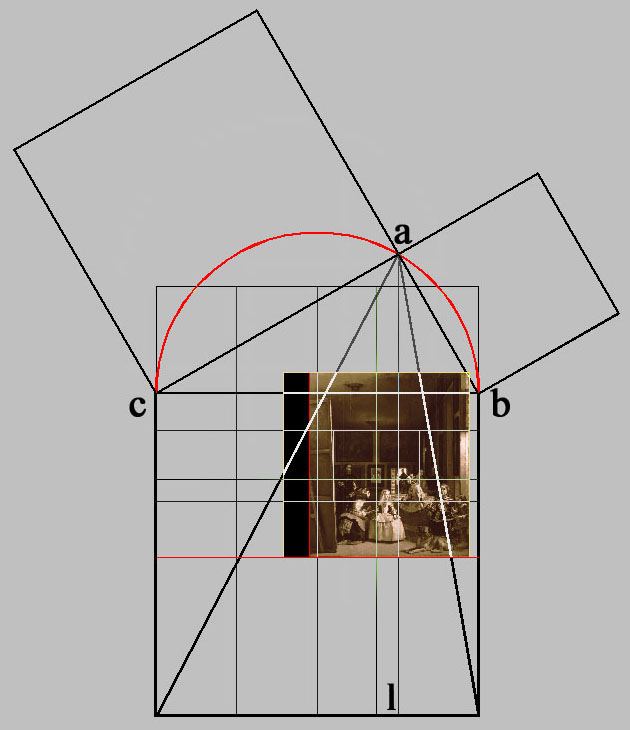
El Ratio, de la raíz latina de razón, que significa medida, va a relacionar los 3,18 metros de la altura de Las Meninas, con el lado de una cuadrícula cuadrada de 150 unidades de lado que hemos dado en llamar:
Límite de la rejilla de 150 unidades.
Esta rejilla formada por 50 x 50 cuadraditos de lado tiene igual hechura que un cuadrado de 3,10 x 3,10 metros, es decir; cada cuadradito mide 3 unidades de lado.
| Sistema castellano | cantidad | unidades | total en unidades | operación | total en metros |
| varas | 3 | 40,5 | 121,5 | 3 x 3 x 0,279 | 2,511 |
| pies | 2 | 13,5 | 27 | 2 x 0,279 | 0,558 |
| pulgadas | 1 | 1,125 | 1,125 | 1 x 0,279/12 | 0,02325 |
| líneas | 4 | 0,09375 | 0,375 | 4 x 0,279/12/12 | 0,00775 |
| 150 | 3,10 metros. |
|
|
Si una pulgada equivale a 1,125 unidades en la cuadrícula de trabajo, entonces; sólo hay que multiplicar 1,125 unidades por 12 para obtener 13,5 unidades, que es la cantidad que representa en esta misma cuadrícula 4,5 cuadraditos valiendo el Pie Real 12 pulgadas.
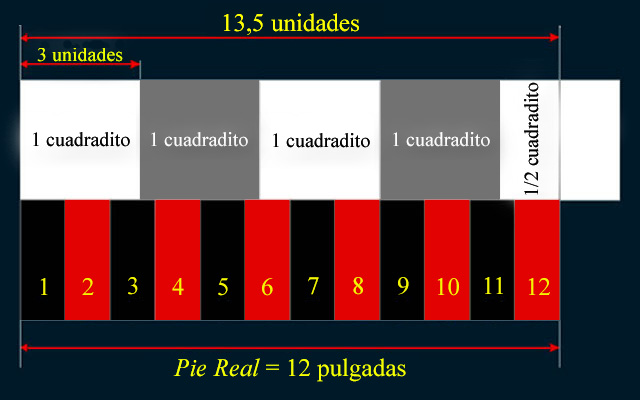 |
|
|
Y gracias a este descubrimiento se explica, pues, que la cuadrícula de 152 unidades es el verdadero mapa al que nos supeditamos, porque es donde quedan situadas, en coordenadas de números enteros, todas las esferas del Árbol Sagrado de la Vida sobre la composición pictórica.
En conclusión, la cuadrícula de 152 unidades de lado delimita, pues, el tamaño de la anchura y altura de la labor geométrica de Las Meninas.
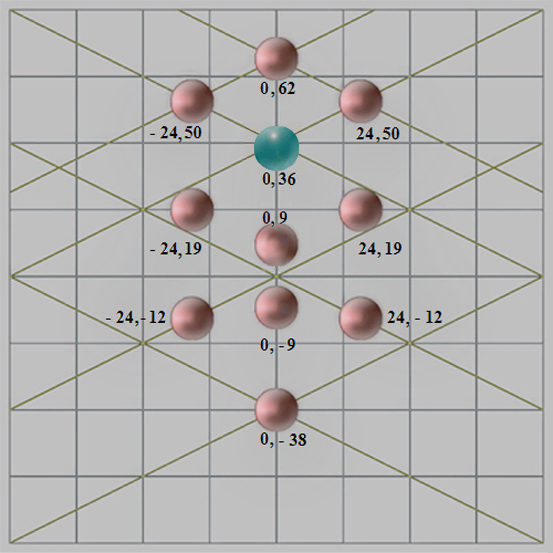 |
Numeración |
Hebreo |
Castellano |
Planeta |
Abscisas - X |
Ordenadas - Y | |
|
I |
כתר |
Kether |
Corona |
0 |
62 | ||
|
II |
חכמה |
Chokmah |
Sabiduría |
24 |
50 | ||
|
III |
בינה |
Binah |
Inteligencia |
Saturno |
- 24 |
50 | |
| דעת |
Dahat |
Conocimiento |
0 |
36 | |||
|
IV |
חסד |
Chesed |
Gracia |
Júpiter |
24 |
19 | |
|
V |
גבורה |
Geburah |
Fortaleza |
Marte |
- 24 |
19 | |
|
VI |
תפארת |
Tipheret |
Hermosura |
Sol |
0 |
9 | |
|
VII |
נצח |
Netzach |
Victoria |
Venus |
24 |
- 12 | |
|
VIII |
הוד |
Hod |
Honor |
Mercurio |
- 24 |
- 12 | |
|
IX |
יסוד |
Yesod |
Fundamento |
Luna |
0 |
- 9 | |
|
X |
מלכות |
Malkhut |
Reino |
Tierra |
0 |
- 38 | |
|
|
Esta cuadrícula, con la que hemos asegurado la posición de las 10 + 1 esferas en coordenadas de números enteros, corresponde a la fase inicial del desarrollo intelectual de Las Meninas, y trasluce, además de un calculado y aritmético soporte, una deliberada reivindicación bajo el logrado naturalismo de esta pintura.
No obstante, ha tomado 350 años reconstruir un plano concluyente que revelara la gestación de la Geometría de este trabajo velazqueño, y, además, que permitiera reconstruir, con rigurosa precisión, la localización de cada elemento principal y necesario de la composición.
 |
|
|
Y sorprende, pues, que desde el inicio del primer capítulo del Sefer Yetzirah, el libro que inspira cada detalle de esta investigación, se perciba la conexión de este texto cabalista con la Geometría, y ésta, a su vez, con la Matemática [3].
Las 22 letras hebreas no son signos convencionales, sino pictogramas de números naturales, ordenados e infinitos, otorgadas a la humanidad en épocas remotas para que con ellas se desvelasen los misterios de la creación.
3 + (3 + 4) + (3 + 4 + 5) = 22
|
|
 |
 |
 |
|
3 = 3 Senderos Horizontales - Letras madres |
7 = (3 + 4) Senderos Verticales - Letras dobles |
12 = (3 + 4 + 5) Senderos Diagonales - Letras simples |
|
עשר ספירות בלי מה ועשרים ושתים אותיות יסוד שלש מאות ושבע כפולות ושתים עשרה פשוטות׃ |
Diez Sefirot en el vacío y veintidós letras de Fundamento: Tres Madres, Siete Dobles y Doce Simples. |
|
Sefer Yetzirah - 1:2 |
Los diez Sefirot más las 22 letras hebreas completan los 32 senderos del Árbol Sagrado de la Vida, número que es la razón por la cual el Sefer Yetzirah, un texto oral de más de veinte siglos de antigüedad, comience del siguiente modo:
Con treinta y dos senderos prodigiosos de Sabiduría grabó Yah.
בשלשים ושתים נתיבות פליאות חכמה חקק יה
Sefer Yetzirah 1:1
|
|
Y se descubre en la primera frase del Sefer Yetzirah la importancia de cada pormenor, y de resaltar, pues, al número 32, el número 32 de la Matemática, de la Geometría y Aritmética, con el que operaremos en la división del perímetro del círculo.
De manera, que el tamaño de la unidad patrón que Diego Velázquez utilizó en la Geometría de Las Meninas depende de la división del perímetro de un Círculo en 320 partes:
360º ÷ 320 = 1,125º
Y su inverso:
1 ÷ 1,125º = 0,888888...º
Pero de igual tamaño que la división del perímetro de un Círculo, de Radio = 4,5 unidades, valiendo Pi = 256/81 = 3,1605..., en 32 partes, de acuerdo con los datos del Problema 48 del Papiro de Ahmes de 1650 a. c.
PERÍMETRO DEL CÍRCULO
|
|
2 × 3,1605... × 4,5 unidades = 28,444444... unidades
28,444444... unidades ÷ 32 = 0,888888... unidades
Y su inverso:
1 ÷ 0,888888... = 1,125
| 9 partes | Unidades | La Pulgada en 9 partes | Pulgadas | Milímetros | ||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 |
| 8/8 | = | 1 | 8/9 | = | 0,888888... | 20,666666... |
|
|
En resumen, para acomodar a los diez Sefirot en coordenadas de unidades enteras, como sucede en Las Meninas, donde además se utiliza el sistema castellano, una pulgada equivale a 1,125 unidades.
Sabemos, pues, que 1,125 unidades equivale a una pulgada castellana, y que la pulgada castellana se divide en doce partes iguales llamadas líneas, por lo que Diego Velázquez, en sus precisas mediciones, fracciona la pulgada castellana en 9 partes iguales para poder operar con la unidad.
8/9 de pulgada equivale a la unidad en este nuevo plano de Las Meninas.
|
9/9 |
8/9 |
7/9 |
6/9 |
5/9 |
4/9 |
3/9 |
2/9 |
1/9 |
|
1,125 |
1 |
0,875 |
0,75 |
0,625 |
0,5 |
0,375 |
0,25 |
0,125 |
| 180º | 160º | 140º | 120º | 100º | 80º | 60º | 40º | 20º |
|
12/12 |
11/12 |
10/12 |
9/12 |
8/12 |
7/12 |
6/12 |
5/12 |
4/12 |
3/12 |
2/12 |
1/12 |
|
1,125 |
1,03125 |
0,9375 |
0,84375 |
0,75 |
0,65625 |
0,5625 |
0,46875 |
0,375 |
0,28125 |
0,1875 |
0,09375 |
| 180º | 165º | 150º | 135º | 120º | 105º | 90º | 75º | 60º | 45º | 30º | 15º |
|
15/15 |
14/15 |
13/15 |
12/15 |
11/15 |
10/15 |
9/15 |
8/15 |
7/15 |
6/15 |
5/15 |
4/15 |
3/15 |
2/15 |
1/15 |
|
1,125 |
1,05 |
0,975 |
0,9 |
0,825 |
0,75 |
0,675 |
0,6 |
0,525 |
0,45 |
0,375 |
0,3 |
0,225 |
0,15 |
0,075 |
| 180º | 168º | 156º | 144º | 132º | 120º | 108º | 96º | 84º | 72º | 60º | 48º | 36º | 24º | 12º |
|
|
Estas tres tablas de divisores del número 1,125 representan, pues, 36 maneras posibles de operar con la pulgada castellana a partir de la apertura de ángulo de tres distintos polígonos regulares, que ofrecen, en los cálculos matemáticos, una absoluta precisión.
 |
||
|
Octodecágono - 18 lados |
Icositetrágono - 24 lados |
Triacontágono - 30 lados |
|
|
||||
| Pulgadas - Fracciones - Grados | ||||
|
Pulgadas (Fracción x/9) |
Pulgadas (Fracción x/12) |
Pulgadas (Fracción x/15) |
||
| Pulgadas | Milímetros | Unidades | ||
| Grados |
CONCLUSIÓN
Al número 1,125 se le podría considerar el número patrón de todas las unidades longitudinales, ya que es una magnitud cuya función no ha variado desde la época de los Sumerios, y, además de ser el resultado de la proporción que cuadra el círculo con un Pi = 256/81, es también el común dividendo, como hemos ya analizado, de la pulgada fraccionada en: 9 - 12 - 15 partes en el sistema de medidas castellano.
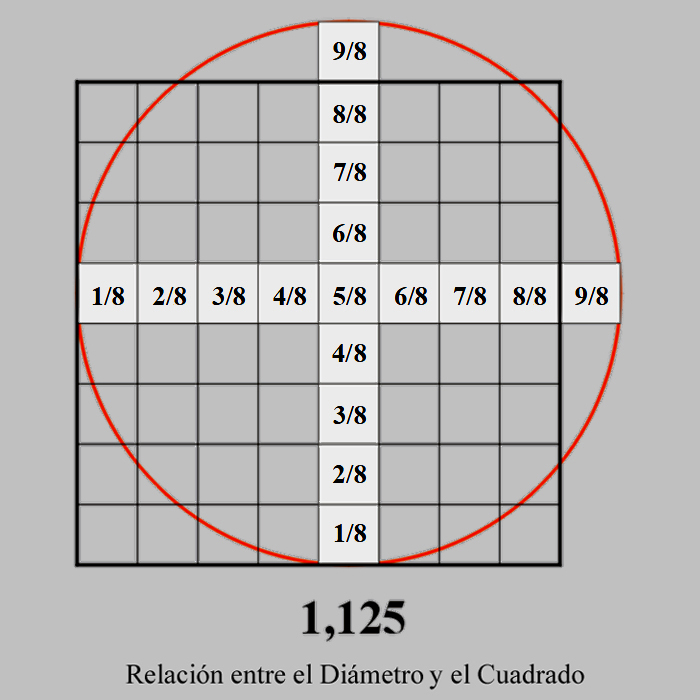 |
Y remontándonos al siglo XXVI a. c., el tamaño de la Pirámide de Kefrén y el número 1,125 se ponen de acuerdo a través de la terna pitagórica.
Veamos:
 |
Terna pitagórica de la Pirámide de Kefrén en metros |
Y operando inversamente con el tamaño real de esta Pirámide egipcia rehabilitaríamos, con total garantía, a los tres guarismos de la terna pitagórica.
| 108 | ÷ |
32 |
= | 3,375 | ÷ | 1,125 | = | 3 |
| 144 | ÷ | = | 4,5 | ÷ | = | 4 | ||
|
180 |
÷ |
= |
5,625 |
÷ |
= |
5 |
Hablamos, pues, de una proporción sesquioctava, que es aquella que contiene la unidad y un octavo de ella:
8/8 + 1/8 = 9/8.
1 + 1/8 = 1,125.
Y es también importante destacar, que en Música al tono pitagórico le corresponde la proporción 9/8, es decir; el ratio entre la quinta y la cuarta:
3/2 ÷ 4/3 = 9/8 = 1,125.
Queda probada, por tanto, la versatilidad del número 1,125, que viene ser un valor constante y de tipo permanente en la aplicación práctica de las cuatro artes liberales del quadrivium, o cuadrivio, es decir; el recurso necesario de cualquiera de las cuatro ciencias de la antigua Grecia y del mundo medieval basadas en un mismo patrón teórico; el número.
Aritmética, Geometría, Astronomía, o Astrología, y Música [4].
Tabla de frecuencias de afinación en la Escala pitagórica
| Nota |
Intervalo |
Tono |
Origen numérico | |||
| Do | Unísono | 1 | = | 1 | = | 1/1 |
| Re b | Segunda menor | 1,05349794239 | = | 28 / 35 | = | 256/243 |
| Do # | Unísono aumentado | 1,06787109375 | = | 37 / 211 | = | 2187/2048 |
| Re | Segunda mayor | 1,125 | = | 32 / 23 | = | 9/8 |
| Mi b | Tercera menor | 1,18518518519 | = | 25 / 33 | = | 32/27 |
| Re # | Segunda aumentada | 1,20135498047 | = | 39 / 214 | = | 19683/16394 |
| Mi | Tercera mayor | 1,265625 | = | 34 / 26 | = | 81/64 |
| Fa | Cuarta justa | 1,33333333333 | = | 22 / 3 | = | 4/3 |
| Sol b | Quinta disminuida | 1,40466392318 | = | 210 / 36 | = | 1024/729 |
| Fa # | Cuarta aumentada | 1,423828125 | = | 36 / 29 | = | 729/512 |
| Sol | Quinta justa | 1,5 | = | 3 / 2 | = | 3/2 |
| La b | Sexta menor | 1,58024691358 | = | 27 / 34 | = | 128/81 |
| Sol # | Quinta aumentada | 1,60180664063 | = | 38 / 212 | = | 6561/4096 |
| La | Sexta mayor | 1,6875 | = | 33 / 24 | = | 27/16 |
| Si b | Séptima menor | 1,7777777777 | = | 24 / 32 | = | 16/9 |
| La # | Sexta aumentada | 1,8020324707 | = | 310 / 215 | = | 59049/32768 |
| Si | Séptima mayor | 1,8984375 | = | 35 / 27 | = | 243/128 |
| Do | Octava | 2 | = | 2 | = | 2 /1 |
Esta tabla prueba que el número 1,125 es la piedra angular de la armonía musical, cuyo valor corresponde a la proporción sesquioctava, 9/8, es decir; el tono pitagórico, el componente fundamental de la música occidental, además de apadrinar el sistema unificado de las medidas geométricas que Velázquez concibió en su obra maestra.
Este hallazgo eleva a Las Meninas a un nuevo nivel de genialidad, ya que el número 1,125 es el hilo conductor de la composición de esta obra, lo que convierte a esta pintura en una sinfonía visual regida por los mismos principios matemáticos que la música de las esferas.
El maestro Diego Velázquez al incorporar esta proporción no sólo demuestra un conocimiento profundo de las ciencias del quadrivium, y de las leyes que rigen a la Aritmética, la Geometría y la Música, sino la interconexión que convierte a este trabajo artístico en una sinfonía de líneas, formas y figuras de música visible, dispuestas según los mismos principios divinos que rigen el cosmos del Árbol de la Vida.
En pintura, la mirada del pintor se propaga en las
distancias, estudia las diferentes calidades de luz claras y oscuras, de tal
manera, que la superficie del lienzo funciona como un plano
transparente, vertical al suelo, en la intersección visual con el modelo.
Y cierto es que 0,279 metros equivalen al Pie Real, y que la anchura de Las Meninas medía 2,79 metros, una anchura que corresponde a diez veces el Pie Real; es decir, a 120 pulgadas.
Una reciprocidad consistente en la que sólo intervienen números enteros.
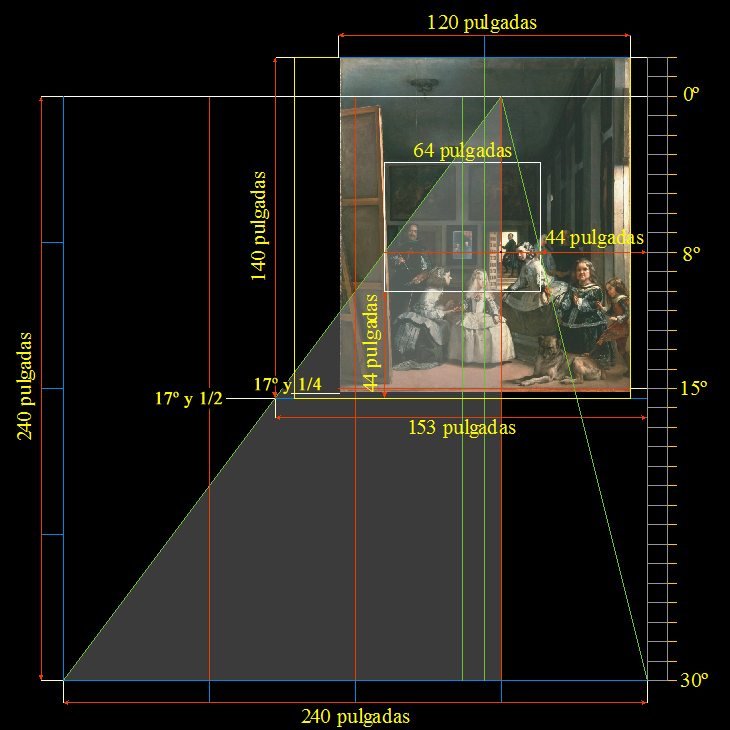 |
Calibración de la anchura y altura del lienzo de Las Meninas
Escala 1:2 |
|
|
Será, por tanto,
la unidad
la quien
defina en Las Meninas
la Aritmética y Geometría del formato
y tamaño de la pared del fondo
pintada en este lienzo.
FORMATO 8
| Formato | Proporción | Pulgadas por unidad | La anchura | Tamaño en metros | ||||
| 8 | 8/9 | = | 0,888888 | x | 72 unidades | = | 64 pulgadas | 8 x 8 x 0,02325 = 1,488 metros |
La anchura de la pared del fondo pintada en el lienzo de Las Meninas mide 1,488 metros
| Formato | Proporción | Pulgadas por unidad | La altura | Tamaño en metros | ||||
| 8 | 8/9 | = | 0,888888 | x | 60 unidades | = | 53,333... pulgadas | 8 x 6,666... x 0,02325 = 1,24 metros |
La altura de la pared del fondo pintada en el lienzo de Las Meninas mide 1,24 metros
 |
La anchura
Tamaño en unidades: 1,125 unidades por pulgada x 64 pulgadas = 72 unidades
La altura
Tamaño en unidades: 1,125 unidades por pulgada x 53 pulgadas y 1/3 = 60 unidades. |
|
|
Se entiende, pues, que trabajando sólo en pulgadas, la escala de representación de la pared del fondo de Las Meninas sería:
240 / 64 = 3,75, y el inverso; 1/3,75 = 0,266666...
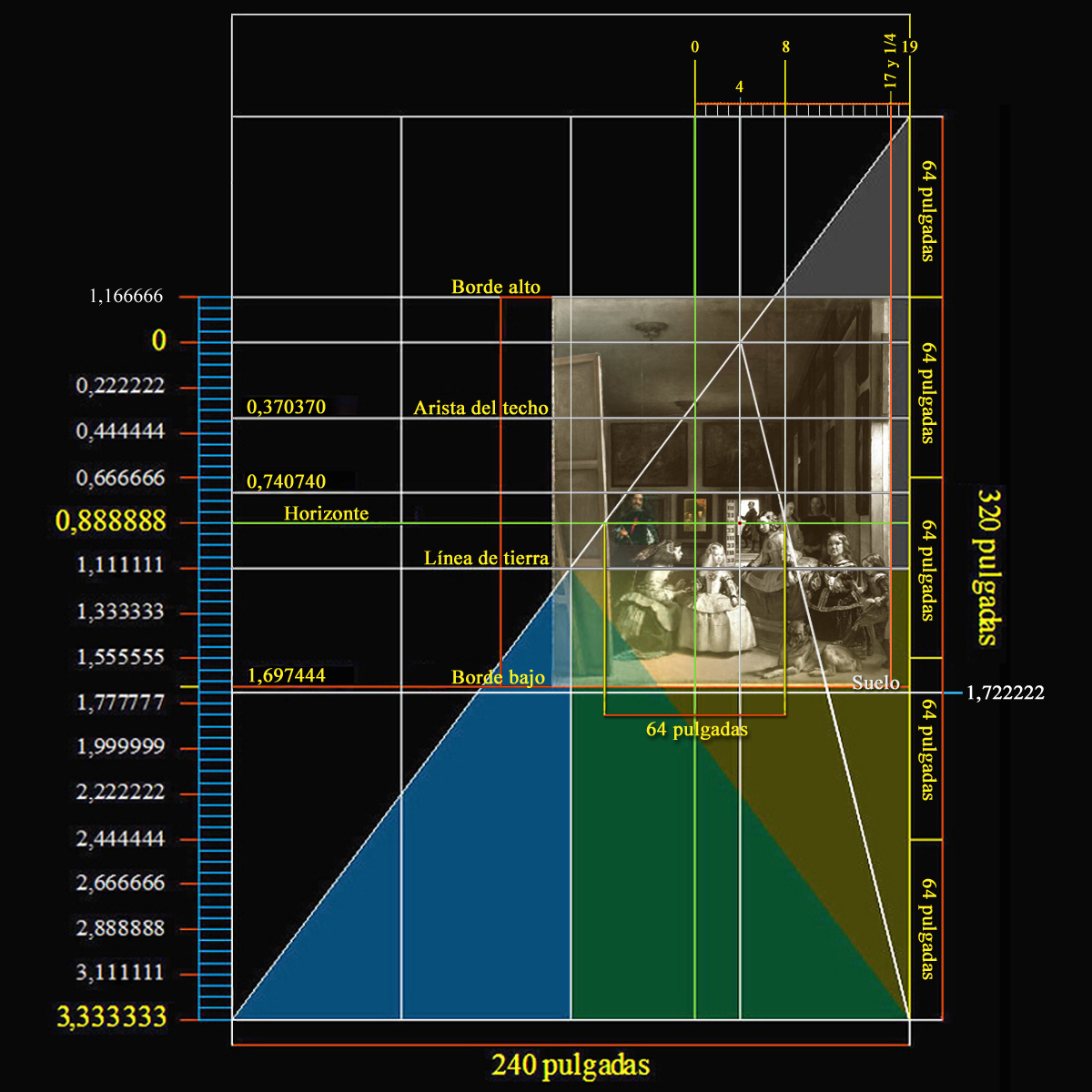
El
Horizonte de la escena de
Las Meninas,
como causa de la realidad perfecta pitagórica,
da acceso
directo al reino de la verdad, e
iguala su altura con la cuarta parte del tamaño de la anchura real de la Habitación del
Príncipe.
|
|
|
Localización de la altura del Horizonte de Las Meninas respecto al suelo de la Habitación del Príncipe. |
Y de igual modo comprobamos que el espacio tridimensional de esta obra maestra depende del talante científico del pintor Diego Velázquez ubicando el punto de fuga X en la coordenada: [18, -12].
Análisis
Sea 60 el tamaño de la anchura de la Habitación del Príncipe, y 18 el valor de la anchura de la pared pintada del fondo en este óleo.
Con estas medidas reseñadas obtendríamos la siguiente razón geométrica en un compás abierto de cuatro puntas:
|
|
|
||||||||||||||||||||||
|
|
La razón geométrica es la comparación de dos cantidades por su cociente, donde se evalúa cuántas veces contiene una a la otra.
El nombre de terna pitagórica deriva del teorema de Pitágoras, y consiste en una secuencia ordenada de tres números enteros positivos; a, c y b, que cumplen con el siguiente requisito:
a² + c² = b²
Escribe Vitrubio en el capítulo II del Libro Noveno de Los Diez Libros de Arquitectura [5]:
Pitágoras inventó una escuadra que no requiere el trabajo de los artesanos, (...).
|
La escuadra perfecta |
|
Si se toman tres reglas, una de tres pies, otra de cuatro y una tercera de cinco, y se las junta de modo que reunidos sus extremos de punta a punta formen un triángulo, se tendrá una escuadra perfecta.
|
Cálculo de la magnitud de la Habitación del Príncipe
y = 60 representaría el tamaño proporcional en pulgadas del ancho la Habitación del Príncipe.
x = 18 representaría el tamaño proporcional en unidades del ancho la pared pintada del fondo en Las Meninas.
60 / 18 = 240 / 72 = 200 / 60 = 10 / 3 = 3,333333... pulgadas por unidad
|
|
|
|
|
Se entiende, pues, que trabajando sólo en pulgadas, la escala de representación de la pared del fondo de Las Meninas sería:
60 / 16 = 3,75, y el inverso; 1/3,75 = 0,266666...
y = 60 representaría el tamaño proporcional en pulgadas del ancho de la Habitación del Príncipe.
x = 16 representaría el tamaño proporcional en pulgadas del ancho de la pared pintada del fondo en Las Meninas
|
|
|
|
Desde la antigüedad la intima relación entre el tamaño aparente y la distancia percibida de un objeto determinado del campo visual quedó reflejada en la denominada Ley de Euclides, que dice así:
La distancia entre el objeto y el observador es inversamente proporcional al tamaño de dicho objeto.
El tamaño de un objeto disminuye en función a la distancia de forma inversamente proporcional, es decir; a doble de distancia a este mismo objeto le corresponde la mitad de su tamaño, fundamento geométrico y óptico que Vitrubio denomina la Proporción.
El filósofo y matemático
francés René Descartes
[6],
contemporáneo al maestro Velázquez, fusionó la geometría y el
álgebra al idear el sistema cartesiano de referencia, en el que la posición de
un punto en el espacio queda representado por las distancias; (x, y,
z), a tres
planos recíprocamente perpendiculares.
Es decir; cualquier punto, fijo o móvil, dentro de una habitación queda definido por tres distancias:
La primera es la horizontal, entre la pared izquierda y la derecha; la anchura x.
La segunda es la vertical, entre el techo y el suelo; la altura y.
Y la tercera es la frontal, entre la pared delantera y la de atrás; la profundidad z [7].
Para el caso que tratamos del plano de Las Meninas sólo necesitaremos dos cantidades:
El eje de abscisas o eje de la x,
y el eje de ordenadas o eje de la y.
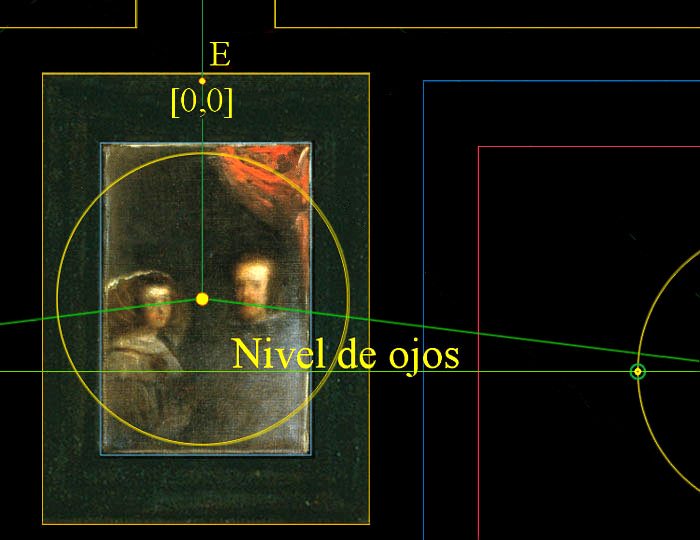 |
|
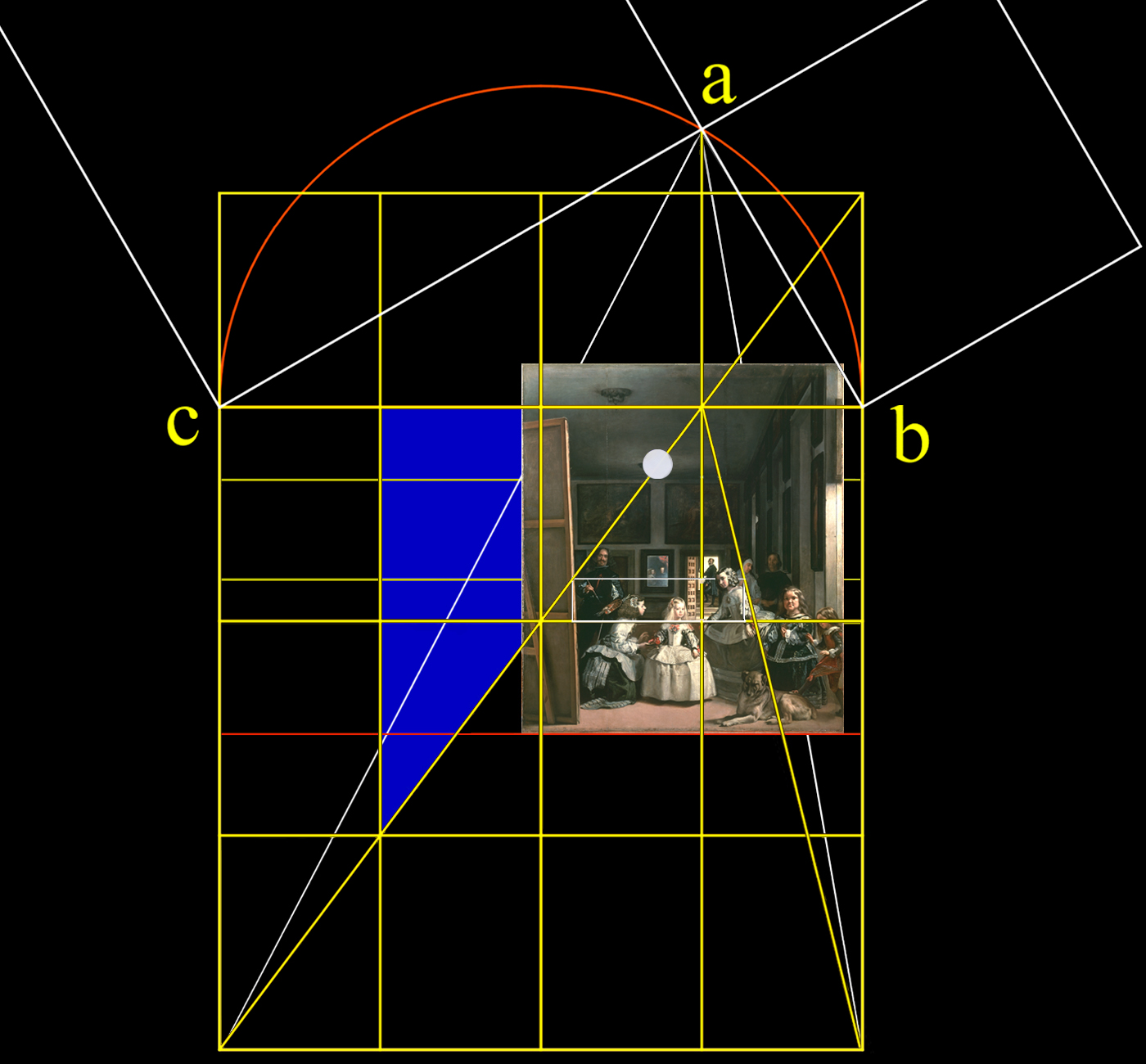
Mostramos, pues, una cuadrícula geométrica emplazada sobre la superficie del lienzo de Las Meninas que ha rescatado del olvido las antiguas medidas de longitud castellanas, y confirmado que en una antigua restauración el tamaño de esta pintura fue levemente alterado, lo cual facilita el trazado exacto del verdadero perímetro o borde limítrofe del lienzo.
0,3 unidades en la rejilla de medición equivalen a:
0,3 unidades /1,125 unidades por pulgada = 0,266666... pulgadas, es decir; 4/15 de pulgada.
0,3 unidades en el mundo real de la pared del fondo equivalen a:
0,3 unidades x 3,333333... pulgadas por unidad = 1 pulgada = 23,25 milímetros.
 |
|
Esta rejilla de medición incluye las medidas del lienzo de Las Meninas y su ubicación respecto al tamaño real de la pared del fondo.
Anchura = 2,761583333 metros - Altura = 3,181375 metros. |
| Pulgadas | Metros | Coeficiente |
| 9 | 9 x 0,02325 = 0,20925 | 2º y 1/4 |
| 16 | 16 x 0,02325 = 0,372 | 4º |
| 32 | 32 x 0,02325 = 0,744 | 8º |
| 43 y 3/15 | 43 y 3/15 x 0,02325 = 1,0044 | 10º y 4/5 |
| 60 | 60 x 0,02325 = 1,395 | 15º |
| 69 | 69 x 0,02325 = 1,60425 | 17º y 1/4 |
| 76 | 76 x 0,02325 = 1,767 | 19º |
| 80 | 80 x 0,02325 = 1,86 | 20º |
| 96 | 96 x 0,02325 = 2,232 | 24º |
| 120 | 120 x 0,02325 = 2,79 | 30º |
| 138 | 138 x 0,02325 = 3,2085 | 34º y 1/2 |
| 140 | 140 x 0,02325 = 3,255 | 35º |
|
|
Aunque no quisiéramos recordar la ingente cantidad de coordenadas que en la superficie de Las Meninas hemos localizado, exactamente: 3371017.216 puntos castellanos [8].
El lienzo de Las
Meninas
en una antigua restauración
fue desmontado de su bastidor original para ser pegado a un nuevo lienzo.
Este reentelado motivó un cambio radical de su formato, ya que el pintor había respetado sin pintura los bordes de los laterales, e hizo visible parte de lienzo que doblaba sobre el bastidor original [9].
Caso Primero
Estudiaremos esta obra artística teniendo en cuenta dos argumentos bien previstos;
el arranque de esta composición como un espacio cuadrado,
y el aspecto final de Las Meninas después de haberse efectuado este estrechamiento o corte por su lateral izquierdo.
Por lo que solaparemos, sobre el canto del lienzo de Las Meninas, el perímetro de un cuadrado, de 155,25 unidades de lado, es decir; de una amplitud igual a un cuadrado de 138 pulgadas castellanas de lado, que hemos denominado:
Borde del orillo del lino original.
 |
Desglose de la anchura de Las Meninas
2,761583333 metros = 133,625 unidades, que equivalen a 118 pulgadas y 7/9.
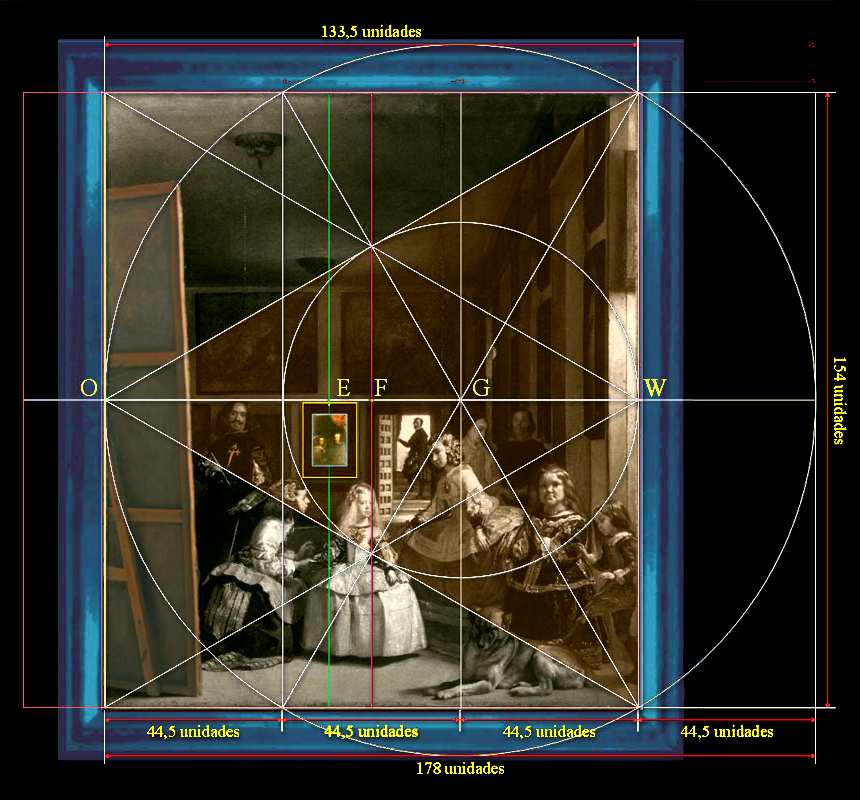
El centro del lienzo de Las Meninas es el punto F |
Y como se puede deducir, la altura del lienzo original de Las Meninas medía el doble del ancho de la distancia entre el punto E, centro absoluto de la Geometría del lienzo de Las Meninas, y el borde del orillo del lino original en el canto derecho del moderno bastidor.
El orillo del lino original de Las Meninas discurre, pues, tangente a lo largo del canto derecho del moderno bastidor.
|
|
|
|
El punto F es el centro de la anchura inicial de Las Meninas que se localiza de dos maneras distintas:
1º caso - En la nariz de la Infanta en la anchura de 2,79 metros, que equivale a 120 pulgadas
2º caso - Sobre el ojo izquierdo de la Infanta Margarita en la anchura de 2,76158333 metros.
Caso Primero
|
El centro verdadero del lienzo de Las Meninas es el punto F en la anchura de 120 pulgadas
Es decir:
|
Sin duda, la anchura, necesariamente, medía 120 pulgadas, que, por otro lado, es la cantidad de pulgadas que corresponden a la mitad de la anchura real de la Habitación del Príncipe.
En definitiva, el tamaño de la altura del lienzo de Las Meninas, antes de ser montado a su bastidor original, era de 138 pulgadas, que equivale a 3,2085 metros.
Caso Segundo
Estudiando detenidamente el lienzo de Las Meninas descubrimos un Caso Segundo, [10] ya que su tamaño actual se ciñe a la particular manipulación matemática a la que fue objeto en la restauración y forración del siglo XIX:
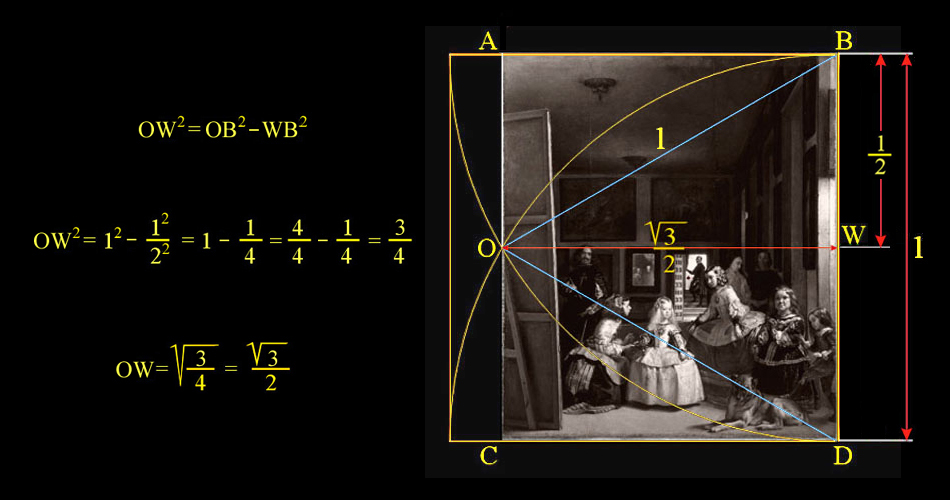
La anchura de esta pintura es igual a la altura multiplicada por la raíz cuadrada de 3 dividida entre 2.
Idea que corresponde al gran triángulo equilátero ODB que limita, su altura OW, la anchura de Las Meninas.
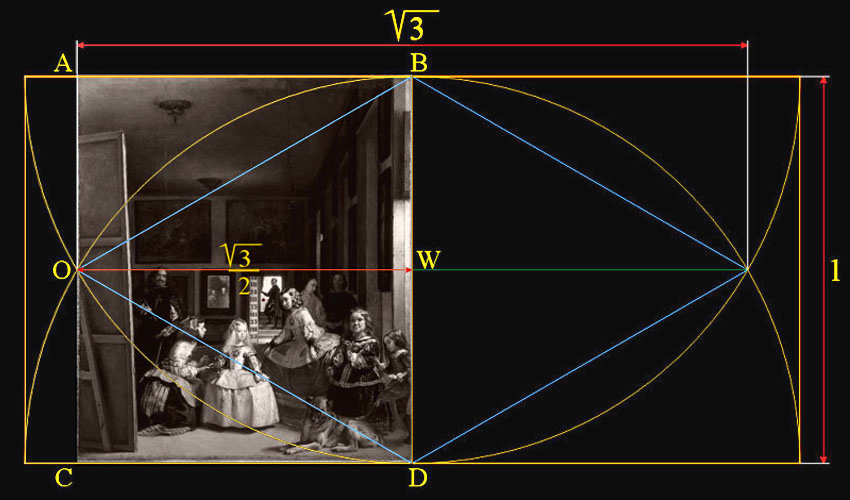 |
|
Estudio de la anchura de Las Meninas en base a la raíz cuadrada de 3 |
La vesica piscis es un símbolo hecho con dos semicírculos del mismo radio, en este caso el radio equivale a la unidad, de manera que el centro de cada círculo, B y D, está en el perímetro de la circunferencia del otro.
Tenemos que BD = BO = OD = 1.
En la antigüedad la razón matemática entre la anchura y la altura de la vesica fue aproximada por el cociente 265/153, que es igual a 1,732026144, y equivalente a √3.
En este Caso Segundo hemos aproximado esta relación al cociente 133,5/154, que es igual a 0,866883116, y equivalente a √3/2, cuya razón geométrica coincide con la del tamaño actual de Las Meninas de acuerdo con el Catálogo del Museo del Prado.
 |
|
|
Desglose de las medidas de Las Meninas
|
Tamaño |
Unidades |
Sistema
castellano |
Sistema métrico |
Museo del Prado |
| Altura |
154 |
136 pulgadas y
8/9 |
3,182666...
metros |
3,18
metros |
| Anchura |
133,5 |
118 pulgadas y
6/9 |
2,759 metros |
2,76 metros |
|
|
Y se entiende, pues, que el eje de simetría de esta pintura se equilibró a partir de un cuadrado para privilegiar a los reyes como centro de la composición; y, aunque actualmente se eche en falta por el lateral izquierdo una franja de 18 pulgadas y 2/9 de ancho, sin embargo, la posición del espejo en el centro de la pared del fondo depende, en la invisibilidad, de este cuadrado.
 |
|
|
|
Unidades |
Pulgadas |
Metros |
| 20,5 | 18 y 2/9 | 0,423666... |
|
|
Leonardo da Vinci ya había escrito [11]:
Y el geómetra reduce toda superficie limitada por líneas a la figura de un cuadrado (...).
E se il Geometra riduce ogni superficie circondata da linee alla figura del quadrato, (...).
|
|
|
|
En el lateral izquierdo, lado AC, hallamos el límite de la relación pitagórica del tamaño de Las Meninas de 3,18 metros de su altura por 2,76 metros de su anchura, y decimos límite porque se puede observar el orillo, o remate del lino del lienzo original, tangente al borde derecho del nuevo bastidor, en el lado opuesto BD.
Gracias al concepto del cuadrado, ÁBC´D, es posible centrar al espejo.
 |
|
|
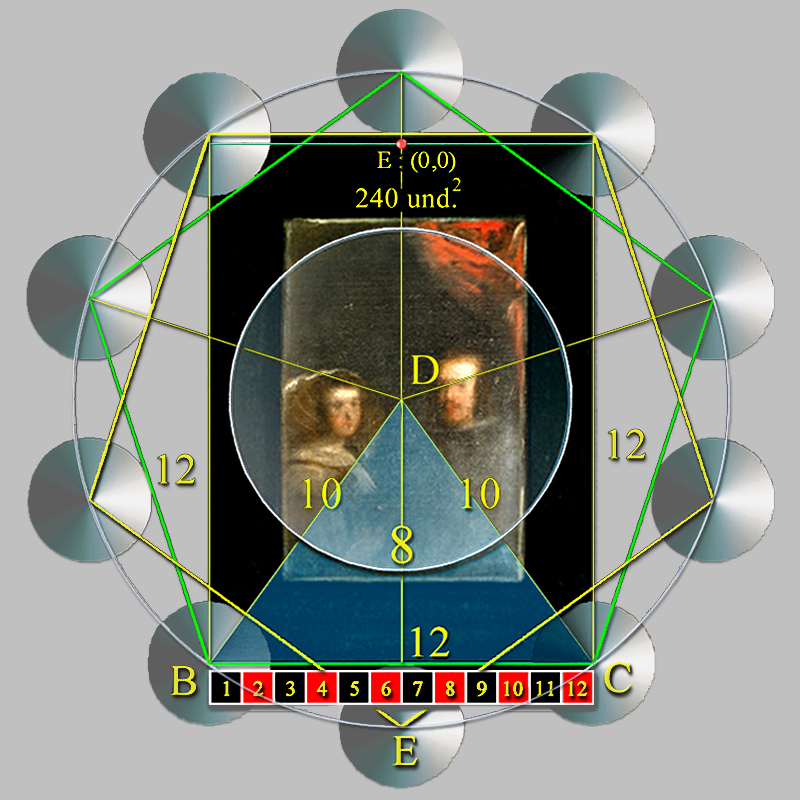
A partir de esta ingeniosa idea, Velázquez elaboró la Geometría del Espejo con la ayuda de dos pentágonos superpuestos, en los que cuatro de sus vértices determinaron su perímetro rectangular, y, en consecuencia, el formato del ancho y alto del marco de madera del Espejo.
El tamaño de 12 unidades del lado del pentágono determinó, pues, el formato del ancho de 12 pulgadas del marco del Espejo de Las Meninas.
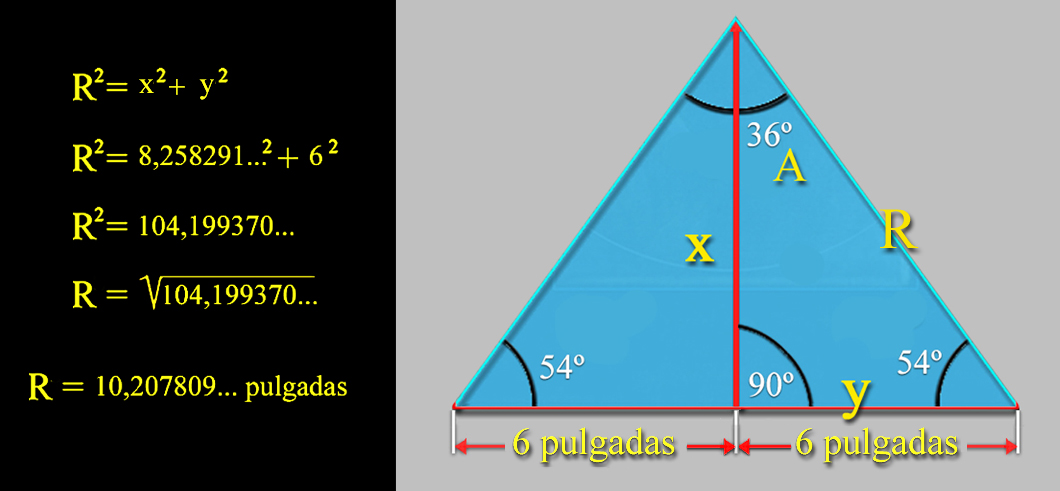
Para el caso que nos ocupa, aplicaremos el Teorema de Pitágoras para averiguar el valor del radio, R, del decágono, que equivale, a su vez, a la mitad de la longitud de la diagonal del Espejo de Las Meninas.
El cuadrado del radio, R, al ser la hipotenusa, es igual a la Apotema, x, de 8,258291... pulgadas al cuadrado, más 6 pulgadas al cuadrado de la mitad del lado del pentágono, y.
 |
|
|
Y obtendríamos 10,214586... pulgadas operando con la altura de 16 y 8/15 pulgadas del marco del Espejo.
| TOLERANCIA |
0,006777... pulgadas |
≈ |
0,157565... milímetros |
Y, en un segundo enfoque trigonométrico, obtendríamos el mismo resultado operando con la Apotema:
|
La Apotema x es igual a 6 pulgadas ÷ tangente 36º ≈ 8,258291... pulgadas
Luego R = 8,258291... pulgadas ÷ seno 54º ≈ 10,207809... pulgadas |
| DIAGONAL DEL ESPEJO |
2 × 10,207809...pulgadas |
≈ |
20,415618 ... pulgadas |
≈ |
12 Φ + 1 |
| TOLERANCIA |
0,000887... unidades |
≈ |
0,000789... pulgadas |
≈ |
0,018344 ... milímetros |
Estos tres tipos de valores representan, pues, una tolerancia muy ajustada, y muy comunes en aplicaciones de alta precisión, como en ingeniería mecánica, fabricación de componentes de precisión, óptica, etc., donde las desviaciones dimensionales permitidas son mínimas.
Caso Tercero
En el siguiente Caso analizaremos las medidas de este lienzo geométricamente a partir del orillo de su lateral derecho; dándose el hecho de que estas medidas de Las Meninas coinciden con el actual tamaño registrado en el Catálogo del Museo del Prado.
 |
|
|
Desglose de las medidas de Las Meninas
| Tamaño | Unidades | Sistema castellano | Sistema métrico | Museo del Prado |
| Altura | 154 | 136 pulgadas y 8/9 | 3,182666... metros | 3,18 metros |
| Anchura | 133,5 | 118 pulgadas y 6/9 | 2,759 metros | 2,76 metros |
|
|
Esencialmente:
Por el punto O pasa la vertical que limita a la anchura del lienzo por su lado izquierdo.
En la parte superior de la moldura del espejo encontramos a E; éste es el centro geométrico y matemático de la rejilla que analizamos, y requisito necesario para poder fijar el origen de coordenadas: [0, 0], de un sutil mapa cartesiano superpuesto a Las Meninas.
Por el punto F surca la línea perpendicular del punto medio de Las Meninas tal cual las contemplamos en el Museo del Prado.
El punto G trata del centro del gran círculo que circunda un triángulo equilátero cuya altura OW limita la anchura de Las Meninas.
El punto G al ser el centro de un triángulo equilátero es el Baricentro, el punto de intersección de las tres medianas, y, también, Incentro de las tres bisectrices de este mismo gran triángulo.
Y aunque el punto F es el centro compositivo de Las Meninas, se le adivina en dos posiciones diferentes; una consecuencia de la anchura actual de esta pintura, y la otra es a causa de la precisa cantidad desestimada de la zona izquierda, lo cual provoca un leve cambio de posición de este centro de composición de la creación velazqueña.
Como hemos ya señalado, el corte por el lateral izquierdo provoca el escamoteo del verdadero centro geométrico de Las Meninas en la parte superior de la moldura negra del espejo con los reyes reflejados en su interior; el punto E.
Estos tres primeros Casos analizados son producto del desarrollo creativo de una pintura tan compleja como son Las Meninas.
Una pauta especial a seguir, y que nos ha ayudado a
entender mejor las cuatro esquinas de este lienzo, ha sido operar con fracciones adecuadas,
que es la condición previa y precisa del geómetra, de la misma manera que en la
antigüedad se utilizaban los números racionales en el cálculo
algebraico [12].
Si hubiéramos mantenido el valor de la anchura de trabajo, es decir; la de 133,625 unidades, entonces el cálculo de la altura sería el siguiente:
133,625 x 2 / √3 = 154,2968594... unidades [13].
Y de acuerdo con el Caso Tercero, es decir; manteniendo la anchura de 133,5 unidades tendríamos:
133,5 x 2 / √3 = 154,1525218... unidades.
Las tres bandas de lienzo
Esta obra está forrada con el sistema tradicional de la gacha. El soporte original está formado por la unión de tres bandas de lienzo de lino, colocadas verticalmente, es decir, en el sentido de su fabricación; la central y la lateral derecha presentan todo el ancho de la tela, ya que se puede observar el orillo en el borde derecho que dobla sobre el bastidor. La banda lateral izquierda es de menor tamaño y no se observa el orillo; tal vez fue cortada por Velázquez, para conseguir unas determinadas dimensiones en la composición... [14].
Dos de las tres bandas de tela que componen el ancho de este lienzo son del mismo tamaño.
|
|
|
|
Caso Cuarto
El lienzo de Las Meninas se compone, pues, de la unión de tres franjas de lienzo cosidas; dos de ellas tienen el ancho de fabricación, y una tercera, más estrecha, completa la anchura total de la tela.
| Banda izquierda | Banda central | Banda derecha | Anchura total del lienzo |
|
31 pulgadas y 4/9 |
43 pulgadas y 2/3 |
43 pulgadas y 2/3 |
118 pulgadas y 7/9 |
|
0,731083333 metros |
1,01525 metros |
1,01525 metros |
2,761583333 metros |
|
|
La investigadora Carmen Garrido Pérez propone en su libro: VELÁZQUEZ, TÉCNICA Y EVOLUCIÓN - MUSEO DEL PRADO, 1992, un ancho de lienzo para la realización de Las Meninas de aproximadamente 105 centímetros.
Esto viene a ser 45 pulgadas x 0,02325 metros la pulgada = 1,04625 metros.
La siguiente ilustración muestra las medidas armónicas necesarias, basadas en el antiguo Pie Real y en sencillas operaciones matemáticas, que hemos formulado adecuadamente, y quizás por primera vez, en el estudio de esta universal obra maestra.
 |
|
|
En color azul destacamos la parte de la anchura del lienzo original que probablemente fuera desestimada por una restauración a principio del siglo XIX.
| Banda izquierda | Banda central | Banda derecha | Anchura del lienzo orignal |
|
32 pulgadas y 2/3 |
43 pulgadas y 2/3 |
43 pulgadas y 2/3 |
120 pulgadas |
|
0,7595 metros |
1,01525 metros |
1,01525 metros |
2,79 metros |
|
|
El corte vertical por el lado izquierdo del lienzo de Las Meninas supuso un estrechamiento severo respecto a su pensada composición inicial cuadrada, aunque investigarlo es el paso necesario para arribar a otro nivel, y ahondar en la estructura simbólica del tema que tratamos.
El tamaño del lienzo de Las Meninas, o
cualquier retrato u objeto pintado de esta bella pintura,
depende íntegramente de las
proporciones regulares.
Caso Quinto
Partimos de las medidas que ya han sido consideradas en el Caso Primero.
Los tamaños de la anchura y altura del lienzo original de Las Meninas miden;
138 pulgadas para la altura,
y 120 pulgadas para la anchura.
Observemos, pues, que el orillo superior del lienzo de Las Meninas se sitúa a 140 pulgadas del suelo de la Habitación del Príncipe representada en este mismo óleo.
 |
|
|
| unidades | pulgadas | metros | medidas castellanas | |
| Altura | 155,25 | 138 | 3,2085 | 138 pulgadas / 12 = 11 pies y medio |
| Anchura | 135 | 120 | 2,79 | 120 pulgadas / 12 = 10 pies |
|
|
|
|
|
|
La anchura de Las Meninas mide 120 pulgadas
Factorización de 2 x 2 x 2 x 3 x 5 = 120.
Los divisores del número 120 son 16:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120.
La altura de Las Meninas mide 138 pulgadas
Factorización de 2 x 3 x 23 = 138.
Los divisores del número 138 son 8:
1, 2, 3, 6, 23, 46, 69, 138.
| LA ALTURA | LA ANCHURA | |||||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||||
| 3,2085 | 138 | 155,25 | = | 155,25 x 1 | 135 x 1 | = | 135 | 120 | 2,79 | |||
| 67,5 x 2 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 77,625 x 2 | 45 x 3 | = | 135 | 120 | 2,79 | |||
| 33,75 x 4 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 51,75 x 3 | 27 x 5 | = | 135 | 120 | 2,79 | |||
| 22,5 x 6 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 25,875 x 6 | 16,875 x 8 | = | 135 | 120 | 2,79 | |||
| 13,5 x 10 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 6,75 x 23 | 11,25 x 12 | = | 135 | 120 | 2,79 | |||
| 9 x 15 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 3,375 x 46 | 6,75 x 20 | = | 135 | 120 | 2,79 | |||
| 5,625 x 24 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 2,25 x 69 | 4,5 x 30 | = | 135 | 120 | 2,79 | |||
| 3,375 x 40 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 1,125 x 138 | 2,25 x 60 | = | 135 | 120 | 2,79 | |||
| 1,125 x 120 | = | 135 | 120 | 2,79 | ||||||||
|
|
| divisiones | cuadrícula | unidades | intervalo en pulgadas | geometría | pulgadas | metros | medidas castellanas | |
| Altura | 23 | 6,75 x 23 | 155,25 | 6,75 ÷ 1,125 = 6 | 23 x 6 | 138 | 3,2085 | 138 pulgadas / 12 = 11 pies y medio |
| Anchura | 20 | 6,75 x 20 | 135 | 20 x 6 | 120 | 2,79 | 120 pulgadas / 12 = 10 pies |
|
|
Al mismo tiempo, siendo el año 1656
cuando fueron pintadas Las Meninas por Diego Velázquez en Madrid,
eventualmente, la cifra de este año está relacionada de manera manifiesta con la
misma cantidad de
líneas castellanas que mide la altura de esta pintura.
Caso Sexto
Primero observemos los 24 divisores del número 1656:
1, 2, 3, 4, 6, 8, 9, 12, 18, 23, 24, 36, 46, 69, 72, 92, 138, 184, 207, 276, 414, 552, 828, 1656.
Y ahora establezcamos y demos nombre a su valor cuantitativo:
| Sistema castellano | varas | pies | palmos | pulgadas | líneas | puntos | metros | unidades |
| 3 y 10/12 | 11 y 6/12 | 15 y 4/12 | 138 | 1656 | 19872 | 3,2085 | 155,25 |
|
|
Por consiguiente, obtendríamos 138 pulgadas dividiendo 1656 líneas castellanas entre 12, resultado que se haya relacionado, a medida del deseo, con la misma cantidad de pulgadas que las del verdadero tamaño de la altura inicial del lienzo que analizamos.
1656 ÷ 12 = 138.
Y de igual manera la anchura funciona con los mismos guarismos:
1656 ÷ 13,8 = 120.
El arquitecto Ramiro Moya en su análisis: El trazado regulador y la perspectiva en Las Meninas, obtuvo las siguientes medidas para este lienzo de Diego Velázquez [15]:
23K para la altura y 20K para la anchura, valiendo K ≈ 1/2 pie = 0,139 metros.
|
LA ALTURA - 11 pies y medio |
LA ANCHURA - 10 pies |
|||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 3,2085 | 138 | 155,25 | = | 6,75 x 23 | 6,75 x 20 | = | 135 | 120 | 2,79 | |
|
|
Aunque el valor de K en nuestras operaciones matemáticas valga 0,1395 metros, que equivale a 6 pulgadas, estamos hablando, pues, de las mismas proporciones del lienzo de Las Meninas.
Y cierto es que el Pie Real mide 0,279 metros, y que la anchura de Las Meninas medía 2,79 metros, es decir, diez veces más; por fortuna una relación proporcional.
En definitiva, hemos establecido el punto de encuentro entre las distintas equivalencias geométricas, matemáticas y de aritmética castellana del tamaño de Las Meninas.
Las medidas del Inventario de 1834
Existe una histórica contradicción a la hora de medir exactamente el lienzo de Las Meninas.
En el Inventario de 1834 del Real Museo de Pinturas, llamado más tarde Museo del Prado, se adjudican al óleo de Las Meninas las siguientes dimensiones:
| La Ynfanta Da Margarita Maria de Austria, hija de Felipe 4o á quien sus damas presentan para vever agua un búcaro (uno de los mas hermosos cuadros del autor). Velazquez. 12,1 x 10,7 Lo Palma 1.100 / 400.000 |
Las medidas del Inventario de 1834 no corresponden, pues, a las dimensiones actuales porque esta pintura se midió con marco.
Caso Séptimo
Veamos:
Medidas del Inventario del año 1834: 12,1 x 10,7.
Estas medidas castellanas corresponden a:
12 pies y 1 pulgada x 10 pies y 7 pulgadas = 145 pulgadas x 127 pulgadas.
Ahora restaremos 7 pulgadas del marco, del alto y ancho, de esta pintura:
145 pulgadas - 7 pulgadas = 138 pulgadas.
127 pulgadas - 7 pulgadas = 120 pulgadas.
Por lo que el ancho del marco medía 3 pulgadas y 1/2.
3,5 pulgadas x 0,02325 metros por pulgada = 0,081375 metros = 8,1375 centímetros.
No dudamos de la exactitud de los
siete Casos
de medición que planteamos, por lo que deberíamos coronar
esta investigación,
necesariamente, con
un octavo Caso
que unifique todo el enfoque geométrico ya propuesto; lo cual implicaría la
representación de todas las relaciones geométricas fundamentales del lienzo de Las
Meninas en un único
plano.
|
|
|
|
Para esta demostración geométrica expondremos las afirmaciones previamente ya establecidas:
El perímetro del lienzo de Las Meninas se sitúa dentro de un cuadrado que mide 155,25 unidades de lado, equivalente a 138 pulgadas.
La anchura geométrica de esta pintura es igual a la altura multiplicada por la raíz cuadrada de 3 dividida entre 2.
El centro de coordenadas de Las Meninas se sitúa en la parte superior de la moldura del espejo en el punto E.
Estas tres consideraciones técnicas son la ayuda necesaria para analizar al lienzo de Las Meninas.
No obstante, nos basaremos en dos ideas complementarias que anticiparon y responden a la génesis geométrica de esta obra maestra:
Una, la del Teorema de Tales de Mileto, que afirma que cualquier ángulo inscrito en un semicírculo es un ángulo recto,
y, la otra, compartida por dos ilustres pensadores; el Teorema de Pitágoras [16], y la proposición 47 de Euclides [17].
El área de trabajo de Las Meninas se origina a partir de la Proposición 47 de Euclides.
|
Cateto menor ab |
Cateto mayor ac |
Hipotenusa cb |
|
1 |
√3 |
2 |
|
120 |
120√3 |
240 |
Terna
pitagórica de la Proposición 47 de Euclides
|
|
 |
|
al describe el eje vertical con el punto de fuga áureo X
al = 2 + √3/2 |
La raíz cuadrada de tres, √3, es un número real positivo, y, corresponde geométricamente al cateto mayor de un triángulo rectángulo.
|
Cateto menor ab |
Cateto mayor ac |
Hipotenusa cb |
|
1 |
√3 |
2 |
Hablamos, pues, de tres cifras concretas que tuvieron una gran utilidad en los cálculos de los constructores del antiguo Egipto:
 |
|
|
Idea que corresponde al mismo concepto que Euclides en la proposición 47, o Teorema de Pitágoras, formuló:
|
En los triángulos rectángulos el cuadrado que es hecho del lado que está opuesto al ángulo recto es igual a los dos cuadrados que son hechos de los lados que contienen el ángulo recto. |
|
DEMOSTRACIÓN
Luego la escala de representación de la pared del fondo será:
64 / 240 = 0,888888... / 3,333333... = 0,266666... = 1 / 3,75. |
 |
|
|
| Lado del Triángulo | Cateto menor | Cateto mayor | Hipotenusa |
| Medidas en pulgadas | 80 x 3 = 240 | 80 x 4 = 320 | 80 x 5 = 400 |
| Divisiones | 60 x 4 partes | 64 x 5 partes | 100 x 4 partes |
|
|
Este plano mide físicamente 240 x 352 pulgadas, es decir; 5,58 x 8,184 metros.
La gestación de la Geometría de Las Meninas está basada, pues, en el Teorema de Pitágoras, y es una característica que se comprueba gráficamente en la precisión del ajuste de la estructura matemática de esta composición:
|
|
|
Localización del punto de fuga del lienzo de Las Meninas |
Cuentan que Pitágoras ideó las delineaciones, las formas, los intervalos, las distancias y las cantidades; entre las cuales halló la virtud de la potencia del triángulo rectángulo, con tanto contentamiento y satisfacción de haberle hallado, que en pago de la merced recibida ofreció a la diosa Minerva el sacrificio Hecatombe en el cual sacrificó cien vacas.
Retomemos, pues, la idea de la terna pitagórica, que, como ya sabemos, consiste en una secuencia ordenada de tres números enteros positivos; a, b y c, que cumplen con el siguiente requisito:
a² + c² = b²
|
a |
b |
c |
|
3 |
4 |
5 |
|
90 |
120 |
150 |
|
120 |
160 |
200 |
|
103,5 |
138 |
172,5 |
|
138 |
184 |
230 |
|
|
Y tal y como se ha probado en el Caso Primero, los tamaños de la anchura y altura del lienzo original de Las Meninas miden;
138 pulgadas para la altura,
y 120 pulgadas para la anchura.
| unidades | pulgadas | metros | medidas castellanas | |
| Altura | 155,25 | 138 | 3,2085 | 138 pulgadas / 12 = 11 pies y medio |
| Anchura | 135 | 120 | 2,79 | 120 pulgadas / 12 = 10 pies |
|
|
Cantidades que, en definitiva, corresponden a dos números concretos localizados en las ternas de la escuadra perfecta de Pitágoras.
Pero, siempre, con la precaución que requiere estos casos tan especiales:
138 pulgadas x 120 pulgadas = 16560 pulgadas cuadradas; que equivalen al área de la superficie del lienzo de Las Meninas, y cuya cantidad representa, pues, diez veces al año 1656, que es el año de la era común de esta pintura.
En España, por ley del 19 de julio de 1849, se adopta el
metro, que es igual a la
diezmillonésima parte del arco de meridiano que va del polo Norte al Ecuador.
La definición actual del metro difiere bastante de la idea primitiva:
1 metro se representa por el trayecto recorrido por la luz en el vacío: 1/299792458... de segundo.
Sea el que fuera el origen del patrón de medidas homologado en el siglo XVIII en la Academia Francesa de la Ciencia, los antiguos egipcios, antes que nadie, fueron los pioneros en asumir el metro.
La consecuencia de la imposición del Sistema métrico francés en la península Ibérica supuso el destierro de la Vara de Burgos, y, lo más imperdonable, el olvido de las medidas castellanas que habían evolucionado, a su vez, a partir del Sistema de medidas pitagórico egipcio.
|
|
|
|
Con el sistema de medidas castellanas de Las Meninas de Diego Velázquez se puede analizar la estructura física de la Pirámide de Kefrén, Egipto, y confirmar varias cuestiones.
Un sistema de medidas castellanas totalmente consistente, normalizado y uniforme, que probaría que en la base de la Pirámide de Kefrén se halla atesorado el patrón de medidas que actualmente denominamos el metro.
El patrón de medidas universales de los maestros egipcios evolucionó paulatinamente de manera distinta en la cuenca mediterránea, hasta que Francia en el siglo XIX estandarizó los diferentes sistema de medidas de la época por el nuevo centesimal, pero, como se deduce en este análisis, la longitud del metro ya se conocía en el siglo XXVI antes de Cristo.
Para el interés del lector, todo encaja en el mismo patrón; el gnomón egipcio centesimal mide un metro, es decir:
53,333333... dedos egipcios = 1000 milímetros.
Para todos los pueblos y para todos los tiempos; como proclamó Napoleón Bonaparte.
Y, en esta investigación, será la medida que revele el número sagrado del Dios arquitecto.
|
Magnitud |
Divisiones | Dedos Egipcios | Milímetros | Unidades Centesimales Egipcias | ||
| Metro | 1000/1000 | 53,333333... | 1000 | 1333,333333... x 1,125/30 | = | 50 |
REGLA
Y si el Metro de Napoleón Bonaparte hubiera nacido a partir de La Vara de Maya, fechada entre 1550 a 1069 a.c., que fue hallada en el Tesoro de Tutankhamon, y actualmente se conserva en el Museo del Louvre, entonces; ¿quién vino primero?:
Pullum vel ovum?
|
|
| Magnitud | Centímetros | Fracción | Centímetros | Operación | Centímetros por Dedo Egipcio | Dedos Egipcio | |||
| Pulgada Castellana | 62 x 1,125/30 | 2,325 | 8/15 | 1,24 | 2,325 / 1,24 | = | 1,875 | 1 | |
| Vara de Maya | 1400 x 1,125/30 | 52,5 | 1/28 | 1,875 | 52,5 / 1,875 | = | 28 | ||
|
|
Definiendo El Tetraktys pitagórico, Francisco Sanchez, Cathedratico de Rhetorica de la Vniuerſidad de Salamanca, en el prólogo del libro séptimo de Arithmetica Practica de Juan Pérez de Moya, comentaba:
A la ſciencia, llamauan dos, porque toda demonſtracion y verdad que prouar queremos, ha de tener fundamento ſobre otra coſa ſabida y cierta, que los Griegos llaman Axioma: & la comprehenſion de eſtas dos coſas, ſe llama ſciencia, ò doctrina.
En este caso tenemos dos sistemas de longitud, aparentemente distintos, que se emparejan.
Y hablamos, pues, de un Sistema Universal Sexagesimal Exacto basado en el número 60 y en el número 4.
Las Unidades de los Maestros Canteros
| 45 partes | Unidades | La Pulgada en 15 partes | Pulgadas | Milímetros | Pulgadas reales | ||
| 45/40 | = | 1,125 | 15/15 | = | 1 | 23,25 | 3,75 |
| 42/40 | = | 1,05 | 14/15 | = | 0,933333 | 21,7 | 3,5 |
| 39/40 | = | 0,975 | 13/15 | = | 0,866666 | 20,15 | 3,25 |
| 36/40 | = | 0,9 | 12/15 | = | 0,8 | 18,6 | 3 |
| 33/40 | = | 0,825 | 11/15 | = | 0,733333 | 17,05 | 2,75 |
| 30/40 | = | 0,75 | 10/15 | = | 0,666666 | 15,5 | 2,5 |
| 27/40 | = | 0,675 | 9/15 | = | 0,6 | 13,95 | 2,25 |
| 24/40 | = | 0,6 | 8/15 | = | 0,533333 | 12,4 | 2 |
| 21/40 | = | 0,525 | 7/15 | = | 0,466666 | 10,85 | 1,75 |
| 18/40 | = | 0,45 | 6/15 | = | 0,4 | 9,3 | 1,5 |
| 15/40 | = | 0,375 | 5/15 | = | 0,333333 | 7,75 | 1,25 |
| 12/40 | = | 0,3 | 4/15 | = | 0,266666 | 6,2 | 1 |
| 9/40 | = | 0,225 | 3/15 | = | 0,2 | 4,65 | 0,75 |
| 6/40 | = | 0,15 | 2/15 | = | 0,133333 | 3,1 | 0,5 |
| 3/40 | = | 0,075 | 1/15 | = | 0,066666 | 1,55 | 0,25 |
|
|
Partimos sabiendo que el valor de 1 pulgada castellana = 23,25 milímetros, que equivalen a 1,125 unidades.
| Unidades | División de la pulgada en 15 partes | Pulgadas | Milímetros | Escala: 1/ 0,266666666 |
| 0,3 | 4/15 | 0,266666... | 6,2 | 3,75 |
|
|
0,3 unidades x 3,75 = 1,125 unidades.
A continuación relacionaremos la pulgada castellana de 23,25 milímetros con el dedo egipcio.
| Magnitud | Divisiones | Cantidad | Fracción | Operación | Milímetros | Proporción | Factorización | ||
| Pulgada Castellana | 12/12 | 1 | 279/12 | = | 620 x 1,125 /30 | = | 23,25 | 124 | 2 x 2 x 31 |
| Dedo Egipcio | 28/28 | 1 | 525/28 | = | 500 x 1,125 /30 | = | 18,75 | 100 | 2 x 2 x 5 x 5 |
|
|
216 piedras de la base de la
Pirámide de Kefrén hacen un total, piedra a piedra, de 216 metros pitagóricos.
 |
Terna pitagórica de la Pirámide de Kefrén en metros |
Factorización de 2 x 2 x 2 x 3 x 3 x 3 = 216.
Los divisores del número 216 son:
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216.
La cantidad de divisores es 16, que no es un valor infinito, y el tamaño de la Pirámide de Kefrén es proporcional al triángulo sagrado egipcio de lados: 3, 4, 5.
Ahora bien, si la base y la altura de la Pirámide de Kefrén están en relación de 2 x 3 a 4; por tanto, hablamos, pues, de la diferencia entre el número que debería ser, y el que no debería ser, acerca de 0,75 metros franceses de menos del ancho de unas piedras mal medidas del siglo XXVI a. c.
Las 216 piedras pitagóricas de la base de la Pirámide de Kefrén miden en metros franceses, más o menos, 215,25 metros.
|
|
|
|
Estas afirmaciones se refutan geométricamente dividiendo la base de 216 metros de la Pirámide de Kefrén entre la anchura de 96 metros de la rejilla de trabajo pitagórica:
216 metros ÷ 96 metros = 2,25 = 1/ 0,444444...
Este resultado es, por tanto, la Escala de la rejilla de trabajo de: 1/0,444444... , es decir; una rejilla de trabajo 2,25 más pequeña que las medidas reales del tamaño de la Pirámide del faraón Kefrén, y que, además, como broche de oro, permite trabajar perfectamente en metros.
PROPORCIÓN
El número Pitagórico de la Base de la Pirámide de Kefrén es igual a 60.
216 metros ÷ 60 = 3,6 metros.
La Proporción entre el Pie Real Castellano y 3,6 metros de la Base de la Pirámide de Kefrén:
0,279 metros ÷ 3,6 metros = 0,0775 = 775/10000 = 31/400.
Una armónica proporción, y que, simultáneamente, restaura el modelo Universal de Geometría.
En la época de Velázquez el Pie Real medía
0,279 metros actuales; que corresponden a
14,88
dedos egipcios.
|
|
|
|
La Vara Castellana mide tres pies, es decir; 0,837 metros, si un Pie Real mide 0,279 metros; y, bajo esta misma premisa, un metro equivale a 43 pulgadas y 1/93, cuando debería representar una cifra, más o menos, entera, es decir; 43 pulgadas.
28 dedos egipcios de 1,875 centímetros cada uno ratifican que la Vara de Maya mide 52,5 centímetros; y, lo más importante, permiten redefinir al Metro francés:
El Metro francés mide, exactamente, 53,333333... dedos egipcios.
Y por otro lado, 14,88 dedos egipcios divididos entre 0,279 metros actuales hacen un total de 53,333333... dedos egipcios por metro.
Hablamos, pues, de la milenaria conexión entre la Vara de Maya del faraón Tutankhamon, el Pie Real Castellano del rey Felipe II y el Metro francés de Napoleón Bonaparte.
|
Magnitud |
Fecha |
Divisiones |
Dedos Egipcios |
Milímetros |
|
Vara de Maya |
1550 a 1069 a.c. |
28/28 |
28 |
525 |
|
Pie Castellano |
1568 |
12/12 |
14,88 |
279 |
|
Metro |
1800 |
1000/1000 |
53,333333... |
1000 |
|
|
El nexo histórico se establece a través de estas sencillas operaciones matemáticas:
|
Magnitud |
Divisiones | Dedos Egipcios | Milímetros | Unidades Centesimales | Centímetros | Unidades Castellanas | |
| 2 Varas de Maya | 56/28 | 56 | 1050 | 1400 x 1,125/15 | 105 | ||
| Metro | 1000/1000 | 53,333333... | 1000 | 1333,333333... x 1,125/15 | 100 | ||
| Vara Castellana | 36/36 | 44,64 | 837 | 1080 x 1,125/30 | 40,5 | ||
| 2 Codos Sagrados | 32/64 | 32 | 600 | 800 x 1,125/15 | 60 | ||
| Vara de Maya | 28/28 | 28 | 525 | 700 x 1,125/15 | 52,5 | ||
| Codo Sagrado | 16/12 | 16 | 300 | 400 x 1,125/15 | 30 | ||
| Pie Castellano | 12/12 | 14,88 | 279 | 360 x 1,125/30 | 13,5 | ||
| Pie Egipcio | 14/28 | 14 | 262,5 | 350 x 1,125/15 | 26,25 | ||
| 1:1000 - Base Kefrén | 1/3 | 11,52 | 216 | 288 x 1,125/15 | 21,6 | ||
| Palmo Castellano | 9/12 | 11,16 | 209,25 | 270 x 1,125/30 | 10,125 | ||
| 1:1000 - Hipotenusa de Kefrén | 1/5 | 9,6 | 180 | 240 x 1,125/15 | 18 | ||
| 1:1000 - Altura de Kefrén | 1/4 | 7,68 | 144 | 192 x 1,125/15 | 14,4 | ||
| Puño Egipcio | 7/28 | 7 | 131,25 | 175 x 1,125/15 | 13,125 | ||
| 1:1000 - 1/2 Base Kefrén | 1/6 | 5,76 | 108 | 144 x 1,125/15 | 10,8 | ||
| Palmo Egipcio | 4/28 | 4 | 75 | 100 x 1,125/15 | 7,5 | ||
| 1/10 Vara de Maya | 140/28 | 2,8 | 52,5 | 70 x 1,125/15 | 5,25 | ||
| Pulgada Egipcia | 2/28 | 2 | 37,5 | 50 x 1,125/15 | 3,75 | ||
| Pulgada Castellana | 15/15 | 1,24 | 23,25 | 30 x 1,125/30 | 1,125 | ||
| La Unidad Castellana | 8/9 | 1,102222... | 20,666666... | 20,666666... x 1,125/30 | 1 | ||
| Dedo Egipcio | 1/28 | 1 | 18,75 | 25 x 1,125/15 | 1,875 | ||
| 8/15 Pulgada Castellana | 8/15 | 0,661333... | 12,4 | 16 x 1,125/30 | 0,6 | ||
| 1/2 Pulgada Castellana | 1/24 | 0,62 | 11,625 | 15 x 1,125/30 | 0,5625 | ||
| La Unidad Egipcia | 10/10 | 0,533333... | 10 | 13,333333... x 1,125/15 | 1 | ||
| 2/12 Pulgada Castellana | 2/12 | 0,206666... | 3,875 | 5 x 1,125/30 | 0,1875 | ||
|
|
El entronque de estos números es seguro, y establecen una relación legítima entre el Sistema Centesimal de 400º de perímetro en la circunferencia y el Sistema Sexagesimal de 360º.
|
Magnitud |
Divisiones | Dedos Egipcios | Milímetros | Unidades Centesimales | Unidades Sexagesimales | |
| Codo Sagrado | 16/12 | 16 | 300 | 400 x 1,125/15 = 30 | ||
| Pie Castellano | 12/12 | 14,88 | 279 | 360 x 1,125/30 = 13,5 |
|
|
Estas medidas no sólo explican las cifras asociadas al espacio y al tiempo en el sistema de medidas de longitud usado en la época de Velázquez, sino que, además, desvelan el estrecho vínculo entre la pulgada castellana y el dedo egipcio.
El sistema de medidas de las Unidades es el puente entre las medidas pitagóricas de la Pirámide de Kefrén y el sistema Sexagesimal de medidas Castellano.
| Sistema | Unidades Castellanas | Unidades Centesimales | Fracción | Milímetros | |
| 2/12 Pulgada Castellana | 0,1875 | 2/12 | 3,875 | ||
| Dedo Egipcio | 0,9375 | 1/28 | 18,75 |
|
|
El Dedo Egipcio de 18,75 milímetros multiplicado por 60" es igual a 1125 milímetros por 1º:
1º = 1125 milímetros x 60" / 18,75 milímetros = 3600"
1125 se relaciona, a su vez, con el decimocuarto número de Aquiles:
72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, 1125...
Y del mismo modo funciona La Vara de Maya de 28 dedos egipcios, que mide 525 milímetros y se conserva en el Museo del Louvre:
28 /1,125 = 24,888888... dedos egipcios por unidades castellanas.
525 milímetros /4,6666666... = 1,125 milímetros.
La analogía, entre la cantidad de 1,125 unidades por pulgada y las piedras de los maestros canteros pitagóricos, hacen posible una histórica y continuada coherencia Aritmética entre los egipcios, los castellanos y los franceses napoleónicos.
Y esto explica, pues, que gracias a la consumada Aritmética pitagórica egipcia, el metro debe medir, exactamente, 1000 milímetros, es decir; 2 Varas de Maya menos 50 milímetros franceses, y que el Pie Real Castellano surgió, ciertamente, después que El Codo Sagrado de 300 milímetros.
notas a pie de página
1 - Página 444 - Iuan Perez de Moya - ARITHMETICA PRACTICA, Y SPECVLATIUA - Salamanca - 1562.
2 - Página 343 – Lib. VIII. PYTHAGORAS. Diogenis Laertii. De vita et moribvs philosophorvm, libri X. Lugduni. M. D. LIX.
En el siglo II Diógenes Laercio cita el libro Suceſſionibus philoſophorum de Alejandro Polyhistor, del siglo I, que relata cómo fue construida la cosmología pitagórica:
Alexandro, en las Sucesiones de los Filósofos, señala acerca de los escritos Pitagóricos lo siguiente: El principio de todas las cosas es la unidad, y de ésta procede la dualidad, que es indefinida, y depende, como materia, de la unidad que la causa. Así, la numeración proviene de la unidad, y de la dualidad indefinida surgen los números; de los números provienen los puntos; de éstos las líneas; de las líneas las figuras planas; de las figuras planas los cuerpos sólidos, los cuales constan de los cuatro elementos; fuego, agua, tierra y aire, que se intercambian y se transforman totalmente el uno en el otro, y de ellos se engendra el mundo animado, intelectual, esférico, con la tierra como centro, también esférica, y habitada en su interior.
Refert autem Alexander in Suceſſionibus philoſophorum, & iſta ſe in Pythagoricis commentarijs notaſſe, principium quidem omnium eſſe unitatem. Porrò ex unitate indefinitam dualitatem, ueluti materiam autori unitate ſubieciſſe. Ex monade verò ac inde terminata dualitate numeros gigni, ex numeris puncta, ex punctis lineas, ex quibus planæ figuræ conſtent. Ex planis autem ſolidas figuras, ex quibus item ſolida conſiſtere corpora, quorum & quatuor elementa eſſe, ignem, aquam, terram, aerem, quæ per omnia ſe mutent ac uertant, ex quibus ſieri mundum animatum, intelligibile, rotundum, mediam terram continentem; quam & ipſam rotundam eſſe & globoſam, ac circum habitari.
3 - El Sefer Yetzirah es el tratado más antiguo del mundo contemplativo hebreo.
|
|
זה השׁער ליהוה צדיקים יבאו בו׃ Esta es la puerta de Jehovah por ella entrarán los justos. Salmo 118:20
Editio princeps del Sefer Yetzirah
ספר יצירה
Libro de la Creación
Mantua 1562 - Editado por Jacob ben Naftali Gazolo |
De acuerdo a Ithamar Gruenwald hay tres primeras versiones del Sefer Yetzirah o Libro de la Creación; una corta, otra larga de algo menos de 2500 palabras y la llamada versión Saadia con comentarios del temprano siglo X.
El Sefer Yetzirah, igual que el libro de la Torah, empieza por la misma letra; por la letra Bet.
Las dos primeras palabras del relato bíblico de la creación:
Berashit bara.
Estas dos letras Bet hacen alusión al misterio de la Creación cuya viva doctrina se desarrolla en el Sefer Yetzirah.
בראשׁית ברא
|
בשלשים ושתים נתיבות פליאות חכמה חקק יה יהוה צבאות אלהי ישראל אלהים חיים ומלך עולם אל שדי רחום וחנון רם ונשא שוכן עד וקדוש שמו מרום וקדוש הוא וברא את עולמו בשלשה ספרים בספר וספר וספור׃ |
1:1 / Con treinta y dos senderos prodigiosos de Sabiduría grabó Yah, el Señor de los Ejércitos, el Dios de Israel, Elohym vivo, Rey del mundo, el Shaddai Misericordioso y Clemente, Elevado y Supremo, que reside en la Eternidad y su nombre es Santo. Y creó Su mundo con tres libros;
|
|
עשר ספירות בלי מה ועשרים ושתים אותיות יסוד שלש מאות ושבע כפולות ושתים עשרה פשוטות׃ |
1:2 / Diez Sefirot en el vacío y veintidós letras de Fundamento: Tres Madres, Siete Dobles y doce Simples. |
|
עשר ספירות בלימה במספר עשר אצבעות חמש כנגד חמש וברית יחיד מכוון באמצע במילת הלשון ובמילת המעור׃ |
1:3 / Diez Sefirot en el vacío: Ordenadas como el número de los diez dedos. Cinco frente a cinco, y la Alianza del Único orientada hacia el centro, como la circuncisión de la lengua y la circuncisión del miembro. |
|
עשר ספירות בלימה עשר ולא תשע עשר ולא אחת עשרה הבן בחכמה וחכם בבינה בחון בהם וחקור מהם והעמד דבר על בוריו והשב יוצר על מכונו׃ |
1:4 / Diez Sefirot en el vacío: Diez y no nueve, diez y no once. Entiende por la Sabiduría y penetra con Inteligencia. Distingue con ellas y escruta desde ellas. Haz que cada cosa se yerga sobre su evidencia y haz que el Formador se siente sobre Su base. |
|
עשר ספירות בלימה מדתן עשר שאין להם סוף עומק ראשית ועומק אחרית עומק טוב ועומק רע עומק רום ועומק תחת עומק מזרח ועומק מערב עומק צפון ועומק דרום אדון יחיד אל מלך נאמן מושל בכולם ממעון קדשו עד עדי עד׃ |
1:5 / Diez Sefirot en el vacío: Su medida es diez que no tienen fin. La profundidad del principio, la profundidad del fin, la profundidad del bien, la profundidad del mal, la profundidad de arriba, la profundidad de abajo, la profundidad del este, la profundidad del oeste, la profundidad del norte, la profundidad del sur. El Maestro único. Dios, Rey fiel, domina sobre todas ellas desde su Santa Morada hasta la Eternidad de las Eternidades. |
|
עשר ספירות בלי מה צפייתן כמראה הבזק ותכליתן אין להם קץ ודברו בהן ברצוא ושוב ולמאמרו כסופה ירדופו ולפני כסאו הם משתחוים׃ |
1:6 / Diez Sefirot en el vacío: Su percepción es como la aparición del relámpago, su límite no tiene fin. Su Verbo se encuentra en ellas, realizando un rápido e incesante movimiento de ida y vuelta. Y su palabra ellas persiguen como en un torbellino, y ante su Trono le rinden alabanzas. |
|
עשר ספירות בלימה נעוץ סופן בתחלתן ותחלתן בסופן כשלהבת קשורה בגחלת שאדון יחיד ואין לו שני ולפני אחד מה אתה סופר׃ |
1:7 / Diez Sefirot en el vacío: Su fin penetra en su principio, y su principio en su fin, como la llama ligada a la brasa. Pues el Maestro es único y no hay quien le sea segundo, y antes del Uno; ¿qué podrías tu contar? |
|
עשר ספירות בלימה בלום פיך מלדבר ולבך מלהרהר ואם רץ פיך לדבר ולבך להרהר שוב למקום שלכך נאמר יחזקאל א') והחיות רצוא ושוב ועל דבר זה נכרת ברית׃) |
1:8 / Diez Sefirot en el vacío: Refrena tu boca de hablar, y tu corazón de meditar. Y si tu corazón se precipitara regresa al lugar. Por eso está escrito: Las Chayot corrían y retornaban. Y sobre esto tuvo lugar una Alianza. |
|
|
La fecha de composición de este texto es causa de debate; la mayoría de los entendidos están de acuerdo en que fue escrito o compilado entre el siglo II y VI.
Sin embargo, Steven M. Wasserstrom ha señalado de una clara transición islámica en el siglo IX, aunque es del todo seguro que ejerció una gran influencia especulativa y mística durante el siglo X.
El comentario de Elliot R. Wolfson remarca:
Propiamente hablando, este trabajo no debería ser definido como una simple composición, y más que nada porque es una composición elaborada a partir de distintas y legendarias literaturas, que han permanecido juntas y enraizadas a través de un complicado proceso de redacción, cuyas etapas no son discernibles.
La mayoría de la versiones del Sefer Yetzirah se componen de seis capítulos cortos de lacónicas declaraciones, similar al tono de los textos Hekhalot o de los tempranos del misticismo del Carro.
Para comprender la importancia de este texto habría que tener bien presente que la Kabala extrajo de su primer capítulo la palabra Sefirot y la noción del estado metafísico de la creación.
Sefer Yetzirah - El Libro de la Creación. Teoría y Práctica, razonado y explicado por Aryeh Kaplan. Editorial Mirach, S. L., 1994.
Título en inglés: Sefer Yetzirah. The Book of Creation. Publicado por acuerdo con Samuel Weiser, Inc. 1990.
4 - Dando al Do el valor de 1 se establece la tabla de frecuencias de afinación.
5 - Página 349 - I DIECI LIBRI DELL´ARCHITETTURA DI M. VITRVVIO. Tradotti & commentati da Monſ. Daniel Barbaro eletto Patriarca d´Aquileia, da lui riueduti & amplati; & hora in piu commoda forma ridotti. In Venetia, MDLXVII.
Libro IX – Cap. II.
Della ſquadra inuentione di Pitagora per formare l´angulo giusto.
Pitagora ſimilmente dimoſtrò la ſquadra ritrouata ſenza opera di artefice alcuno, & fece chiato con quanto grande fatica i fabri facendola, a pena la poſſono al giuſto ridurre. Queſta coſta con ragioni, & uie emendata, da ſuoi precetti ſi manifeſta: perque ſe egli ſi prenderà tre regole, una di piedi tre, l´altra di quattro, la terza di cinque, & queſte regole compoſte ſiano, che con i capi ſi tocchino inſieme facendo una figura triangulare, condurranno la ſquadra giuſta.
6 - René Descartes, 1596-1650, filósofo y matemático francés latinizó su nombre como Renatus Cartesius, de donde procede la denominación de sistema y coordenadas cartesianas de la Geometría Analítica que él ideó.
En 1637 Descartes publicaba los hallazgos de la Geometría Analítica usando un conjunto de ejes y coordenadas en un apéndice al Discurso del Método; esta nueva Geometría facilitaba representar las rectas, curvas y figuras geométricas mediante el valor numérico de las expresiones algebraicas.
Los diagramas y coordenadas cartesianas fueron a partir de René Descartes una de las herramientas más empleadas y útiles en el estudio de las matemáticas.
Recordaremos en qué consiste un diagrama cartesiano usado en un plano de dos dimensiones:
Diagrama cartesiano
El plano se divide en cuatro partes llamadas cuadrantes mediante dos rectas perpendiculares entre sí, la horizontal y la vertical respectivamente.
Dichas rectas se cortan en un punto que recibe el nombre de origen de coordenadas; cuya posición es la coordenada (0,0).
Las rectas se dividen en segmentos de igual longitud y a cada marca del segmento se le asigna un número entero.
En la recta horizontal, llamada eje de abscisas o eje de las x, al punto de corte con la otra recta se le asigna el 0 y hacia la derecha el 1, 2,..., y hacia la izquierda el -1, -2,... y así sucesivamente en ambas direcciones.
De forma análoga se procede con la recta vertical, llamada eje de ordenadas o eje de las y, al punto de corte con la otra recta se le asigna el 0 y hacia arriba el 1,2,...., y hacia abajo el -1,-2,... y así sucesivamente en ambas direcciones.
De modo que tenemos la situación del dibujo.
|
|
Así pues, cada punto del plano se localiza mediante dos números correspondientes a cada eje, que se escriben encerrados entre paréntesis y separados por una coma (,).
Dicho par de números se llaman coordenadas.
Y se obtienen, por ejemplo, de la siguiente manera:
El punto de coordenadas (2,3) se localiza situándonos en el punto marcado con el 2 en el eje de las “x”; una vez aquí, subimos paralelamente al eje de las “y”, hasta el lugar marcado en este eje con el 3.
De igual forma para el punto (-3,2), nos situamos en la marca -3 del eje “x” y subimos verticalmente hasta el 2 del eje “y”.
7 - El esquema del tamaño de las distintas proporciones, de la anchura y altura de la pared del fondo de Las Meninas, parte de un punto, es decir; desde el punto de fuga, coordenada X = [18 , -12], pero su trazado está basado en el Primer Teorema de Thales de Mileto, que vivió hacia el año 600 a. de C.
Primera Tabla
Formatos en base al tamaño de la anchura de 72 unidades de la pared del fondo:
|
formato |
proporción |
|
escala |
|
unidades |
|
pulgadas |
metros |
|
La anchura de la Habitación del Príncipe mide 5,58 metros |
||||||||
|
30 |
30/9 |
= |
3,333.333 |
x |
72 |
= |
240 |
30 x 8 x 0,02325 = 5,58 |
|
29 |
29/9 |
= |
3,222.222 |
x |
72 |
= |
232 |
29 x 8 x 0,02325 = 5,394 |
|
28 |
28/9 |
= |
3,111.111 |
x |
72 |
= |
224 |
28 x 8 x 0,02325 = 5,208 |
|
27 |
27/9 |
= |
2,999.999 |
x |
72 |
= |
216 |
27 x 8 x 0,02325 = 5,022 |
|
26 |
26/9 |
= |
2,888.888 |
x |
72 |
= |
208 |
26 x 8 x 0,02325 = 4,836 |
|
25 |
25/9 |
= |
2,777.777 |
x |
72 |
= |
200 |
25 x 8 x 0,02325 = 4,65 |
|
24 |
24/9 |
= |
2,666.666 |
x |
72 |
= |
192 |
24 x 8 x 0,02325 = 4,464 |
|
23 |
23/9 |
= |
2,555.555 |
x |
72 |
= |
184 |
23 x 8 x 0,02325 = 4,278 |
|
22 |
22/9 |
= |
2,444.444 |
x |
72 |
= |
176 |
22 x 8 x 0,02325 = 4,092 |
|
21 |
21/9 |
= |
2,333.333 |
x |
72 |
= |
168 |
21 x 8 x 0,02325 = 3,906 |
|
20 |
20/9 |
= |
2,222.222 |
x |
72 |
= |
160 |
20 x 8 x 0,02325 = 3,72 |
|
19 |
19/9 |
= |
2,111.111 |
x |
72 |
= |
152 |
19 x 8 x 0,02325 = 3,534 |
|
18 |
18/9 |
= |
1,999.999 |
x |
72 |
= |
144 |
18 x 8 x 0,02325 = 3,348 |
|
17 |
17/9 |
= |
1,888.888 |
x |
72 |
= |
136 |
17 x 8 x 0,02325 = 3,162 |
|
16 |
16/9 |
= |
1,777.777 |
x |
72 |
= |
128 |
16 x 8 x 0,02325 = 2,976 |
|
15 |
15/9 |
= |
1,666.666 |
x |
72 |
= |
120 |
15 x 8 x 0,02325 = 2,79 |
|
14 |
14/9 |
= |
1,555.555 |
x |
72 |
= |
112 |
14 x 8 x 0,02325 = 2,604 |
|
13 |
13/9 |
= |
1,444.444 |
x |
72 |
= |
104 |
13 x 8 x 0,02325 = 2,418 |
|
12 |
12/9 |
= |
1,333.333 |
x |
72 |
= |
96 |
12 x 8 x 0,02325 = 2,232 |
|
11 |
11/9 |
= |
1,222.222 |
x |
72 |
= |
88 |
11 x 8 x 0,02325 = 2,046 |
|
10 |
10/9 |
= |
1,111.111 |
x |
72 |
= |
80 |
10 x 8 x 0,02325 = 1,86 |
|
9 |
9/9 |
= |
0,999.999 |
x |
72 |
= |
72 |
9 x 8 x 0,02325 = 1,674 |
|
La anchura de la pared del fondo pintada en el lienzo de Las Meninas mide 1,488 metros |
||||||||
|
8 |
8/9 |
= |
0,888.888 |
x |
72 |
= |
64 |
8 x 8 x 0,02325 = 1,488 |
|
7 |
7/9 |
= |
0,777.777 |
x |
72 |
= |
56 |
7 x 8 x 0,02325 = 1,302 |
|
6 |
6/9 |
= |
0,666.666 |
x |
72 |
= |
48 |
6 x 8 x 0,02325 = 1,116 |
|
5 |
5/9 |
= |
0,555.555 |
x |
72 |
= |
40 |
5 x 8 x 0,02325 = 0,93 |
|
4 |
4/9 |
= |
0,444.444 |
x |
72 |
= |
32 |
4 x 8 x 0,02325 = 0,744 |
|
3 |
3/9 |
= |
0,333.333 |
x |
72 |
= |
24 |
3 x 8 x 0,02325 = 0,558 |
|
2 |
2/9 |
= |
0,222.222 |
x |
72 |
= |
16 |
2 x 8 x 0,02325 = 0,372 |
|
1 |
1/9 |
= |
0,111.111 |
x |
72 |
= |
8 |
1 x 8 x 0,02325 = 0,186 |
|
0 |
0/9 |
= |
0,000.000 |
x |
72 |
= |
0 |
0 x 8 x 0,02325 = 0 |
|
|
|
|
|
|
Segunda Tabla
Formatos en base al tamaño de la altura de 59,4 unidades de la pared del fondo:
|
formato |
proporción |
|
escala |
|
unidades |
|
pulgadas |
metros |
|
La altura de la Habitación del Príncipe mide 4,65 metros |
||||||||
|
30 |
30/9 |
= |
3,333.333 |
x |
60 |
= |
200 |
30 x 6,666 x 0,02325 = 4,65 |
|
29 |
29/9 |
= |
3,222.222 |
x |
60 |
= |
193 y 1/3 |
29 x 6,666 x 0,02325 = 4,495 |
|
28 |
28/9 |
= |
3,111.111 |
x |
60 |
= |
186 y 2/3 |
28 x 6,666 x 0,02325 = 4,34 |
|
27 |
27/9 |
= |
2,999.999 |
x |
60 |
= |
180 |
27 x 6,666 x 0,02325 = 4,185 |
|
26 |
26/9 |
= |
2,888.888 |
x |
60 |
= |
173 y 1/3 |
26 x 6,666 x 0,02325 = 4,03 |
|
25 |
25/9 |
= |
2,777.777 |
x |
60 |
= |
166 y 2/3 |
25 x 6,666 x 0,02325 = 3,875 |
|
24 |
24/9 |
= |
2,666.666 |
x |
60 |
= |
160 |
24 x 6,666 x 0,02325 = 3,72 |
|
23 |
23/9 |
= |
2,555.555 |
x |
60 |
= |
153 y 1/3 |
23 x 6,666 x 0,02325 = 3,565 |
|
22 |
22/9 |
= |
2,444.444 |
x |
60 |
= |
146 y 2/3 |
22 x 6,666 x 0,02325 = 3,41 |
|
21 |
21/9 |
= |
2,333.333 |
x |
60 |
= |
140 |
21 x 6,666 x 0,02325 = 3,255 |
|
20 |
20/9 |
= |
2,222.222 |
x |
60 |
= |
133 y 1/3 |
20 x 6,666 x 0,02325 = 3,1 |
|
19 |
19/9 |
= |
2,111.111 |
x |
60 |
= |
126 y 2/3 |
19 x 6,666 x 0,02325 = 2,945 |
|
18 |
18/9 |
= |
1,999.999 |
x |
60 |
= |
120 |
18 x 6,666 x 0,02325 = 2,79 |
|
17 |
17/9 |
= |
1,888.888 |
x |
60 |
= |
113 y 1/3 |
17 x 6,666 x 0,02325 = 2,635 |
|
16 |
16/9 |
= |
1,777.777 |
x |
60 |
= |
106 y 2/3 |
16 x 6,666 x 0,02325 = 2,48 |
|
15 |
15/9 |
= |
1,666.666 |
x |
60 |
= |
100 |
15 x 6,666 x 0,02325 = 2,325 |
|
14 |
14/9 |
= |
1,555.555 |
x |
60 |
= |
93 y 1/3 |
14 x 6,666 x 0,02325 = 2,17 |
|
13 |
13/9 |
= |
1,444.444 |
x |
60 |
= |
86 y 2/3 |
13 x 6,666 x 0,02325 = 2,015 |
|
12 |
12/9 |
= |
1,333.333 |
x |
60 |
= |
80 |
12 x 6,666 x 0,02325 = 1,86 |
|
11 |
11/9 |
= |
1,222.222 |
x |
60 |
= |
73 y 1/3 |
11 x 6,666 x 0,02325 = 1,705 |
|
10 |
10/9 |
= |
1,111.111 |
x |
60 |
= |
66 y 2/3 |
10 x 6,666 x 0,02325 = 1,55 |
|
9 |
9/9 |
= |
0,999.999 |
x |
60 |
= |
60 |
9 x 6,666 x 0,02325 = 1,395 |
|
La altura de la pared del fondo pintada en el lienzo de Las Meninas mide 1,24 metros |
||||||||
|
8 |
8/9 |
= |
0,888.888 |
x |
60 |
= |
53 y 1/3 |
8 x 6,666 x 0,02325 = 1,24 |
|
7 |
7/9 |
= |
0,777.777 |
x |
60 |
= |
46 y 2/3 |
7 x 6,666 x 0,02325 = 1,085 |
|
6 |
6/9 |
= |
0,666.666 |
x |
60 |
= |
40 |
6 x 6,666 x 0,02325 = 0,93 |
|
5 |
5/9 |
= |
0,555.555 |
x |
60 |
= |
33 y 1/3 |
5 x 6,666 x 0,02325 = 0,775 |
|
4 |
4/9 |
= |
0,444.444 |
x |
60 |
= |
26 y 2/3 |
4 x 6,666 x 0,02325 = 0,62 |
|
3 |
3/9 |
= |
0,333.333 |
x |
60 |
= |
20 |
3 x 6,666 x 0,02325 = 0,465 |
|
2 |
2/9 |
= |
0,222.222 |
x |
60 |
= |
13 y 1/3 |
2 x 6,666 x 0,02325 = 0,31 |
|
1 |
1/9 |
= |
0,111.111 |
x |
60 |
= |
6 y 2/3 |
1 x 6,666 x 0,02325 = 0,155 |
|
0 |
0/9 |
= |
0,000.000 |
x |
60 |
= |
0 |
0 x 6,666 x 0,02325 = 0 |
|
|
8 - Hemos operado con vectores de un grosor de una milésima de milímetro, 0,001 mm., y una certidumbre de una diezmilésima de unidad en los resultados que aportamos, es decir; de un margen de seguridad de 0,0001 de unidad.
A partir de la siguiente tabla de equivalencias se construye la rejilla de trabajo; no obstante, estamos hablando de la existencia de una abultada cantidad de coordenadas posibles y de una manera practica de medir la superficie de este lienzo.
Y en la posibilidad de fragmentar la rejilla de trabajo en tantas partes como sea oportuno.
| Sistema de medidas | Anchura | Altura | Coordenadas | ||
| metros | 2,76158333 | x | 3,181375 | = | 8,785632... |
| unidades | 133,6250 | x | 153,9375 | = | 20.569,8984375 |
| pulgadas | 118 y 7/9 | x | 136 y 10/12 | = | 16.252,759258... |
| líneas | 1.425 y 4/12 | x | 1.642 | = | 21340.397 y 4/12 |
| puntos | 17.104 | x | 19.704 | = | 3371017.216 |
|
|
L
a imagen de Las Meninas mide gráficamente:
133,6250 unidades por 153,9375 unidades.
9 - Entre una a dos pulgadas del perímetro actual de Las Meninas se ocultaba en el canto de la madera de su primer bastidor. Esta cantidad oscila, según el lado que analicemos, respecto a la superficie efectiva del área de trabajo del pintor.
Los reentelados de los cuadros implican la fijación de la pintura y su soporte sobre otra tela a través de diferentes materiales adhesivos. La unión de una tela a otra se realiza mediante calor. La delicadeza y la perfección con las que el restaurador realice esta operación influyen en la mayor o menor transformación de las pinturas.
Página 61 - Nota 6 - VELÁZQUEZ, TÉCNICA Y EVOLUCIÓN - Carmen Garrido Pérez - MUSEO DEL PRADO. 1992.
10 - Recordaríamos el paralelismo entre el alzado geométrico de Las Meninas y el debate en relación a la construcción de la catedral de Milán en 1398.
Expertos de varios países se centraron en la forma geométrica de elevar la catedral, algunos opinaron que AD QUADRATUM, es decir; partiendo sobre la base de un cuadrado, y otros AD TRIANGULUM, es decir; partiendo de un triángulo equilátero.
Finalmente, el asesoramiento del matemático Gabriele Stornaloco, de Piacenza, concibió el alzado principal y la sección transversal AD TRIANGULUM, pero esta decisión planteaba el problema de medir la altura en múltiplos y submúltiplos de √3; y los arquitectos, que manejaban un control de proporciones basado en números enteros, no podrían saber la altura de antemano, sino en el curso de la construcción.
11 - 12 [ Urb. 19b, 20a ] DE COMO LA ASTROLOGÍA NACE DEL OJO, PORQUE EN EL OJO ES ENGENDRADA
Página 41 - Tratado de Pintura – Leonardo da Vinci. Editora Nacional. Ángel González García.
12 - Es significativo que Velázquez poseyera el libro de Geometría de Andrés García de Céspedes, impreso en 1606.
La portada de este libro reza así:
Libro de instrumentos nuevos de Geometría muy necesarios para medir distancias, y alturas, sin que intervengan números, como se demuestra en la práctica (...).
Página 138, Catálogo de Pedro Ruiz Pérez: De la Pintura y las Letras. La Biblioteca de Velázquez, editado por: E. P. G. Conserjería de Cultura. Junta de Andalucía.
Los únicos números a tratar en Las Meninas estarían ya resueltos en el trazado primoroso de una impecable cuadrícula sobre el lienzo.
John F. Moffit puntualiza sobre este asunto:
El encuadre arquitectónico de Las Meninas, identificado en nuestra ya publicada investigación, fue recreado con absoluta precisión, y por ello, e indudablemente, con la ayuda de algún tipo de ingenio mecánico. De acuerdo con ello, como nosotros creemos ( y la prueba absoluta probablemente requeriría raspar el cuadro hasta la preparación ) , Velázquez debió de cubrir primeramente el lienzo con un sistema lineal o de rejilla ( probablemente impuesto sobre la superficie con finas líneas de carboncillo ) y casi con seguridad con retículas individuales de ½ o un pie para cada subcuadrado ( 1 pie = 1/3 de vara = 0,278 metros ) . Esta retícula correspondería a la plantilla de la pantalla cuadriculada de tamaño reducido, que utilizaban tradicionalmente los pintores, el marco de perspectiva, esto es, “el velo” descrito primeramente por León Battista Alberti ( en su Della Pintura, libro que estaba en la biblioteca de Velázquez ) . Dados algunos precedentes históricos y físicos, casi con seguridad esta retícula pudo ser grabada en la placa visual de una cámara oscura.
Página 182 - Anatomía de Las Meninas; realidad, ciencia y arquitectura. Boletín del Museo del Prado. Septiembre-Diciembre 1986.
Nuestro comentario
Según los cálculos de John F. Moffit media vara mediría 0,4175 metros.
En este nuevo plano 3 unidades es el equivalente al lado de cada uno de los cuadraditos que usamos, y miden el resultado de dividir 3,10 metros, la altura de la rejilla de 150 unidades, entre 50 cuadraditos, es decir; 0,062 metros; lo que representaría que cada cuadradito mediría, entonces, 2 pulgadas y 2/3 de pulgada.
Comprobación:
Por conveniencia matemática, usamos el pie con un valor de 0,279 metros.
Si un Pie Real, que son 12 pulgadas, es equivalente a 0,279 metros, 0,062 metros equivaldrá al resultado que buscamos.
|
12 pulgadas |
0,279 metros |
|
2,666666666 pulgadas equivalente a 2 pulgadas y 2/3 de pulgada |
0,062 metros |
LA HISTORIA
En el año 1567, tras fracasar el Ordenamiento de Montalvo en 1484, Felipe II había promulgado la «Nueva Recopilación de las Leyes de España» para acabar con el caos legislativo.
Este Código recopilado de las Leyes del Fuero Real, de las 18 Leyes de Toro, del Ordenamiento de Alcántara y el de Montalvo, incluye la pragmática dictada por el rey prudente desde El Escorial, 24 de junio de 1568, en la que establece que:
(...) la vara castellana que se ha de usar en todos estos reynos, sea la que hay, y tiene, la ciudad de Burgos (...)
En el Museo de Aparatos del Centro Geográfico del Ejército de Tierra existen dos patrones del pie de Burgos; uno de ellos procedente del Cuerpo Nacional de Ingenieros y el otro del Cuerpo del Estado Mayor del Ejército.
Sus nombres concretos son:
Pie de Burgos en latón, construido por el Cuerpo Nacional de Ingenieros. Madrid 1821. Dirección de Valencia y Murcia.
Pie Cuerpo del Estado Mayor del Ejército. Capitanía General de Aragón. Año 1846.
Estos dos viejos patrones castellanos están divididos en dedos y doceavos de dedo, cuya equivalencia sería:
1 pie = 16 dedos = 192 doceavos de dedo = 0,278635 m.
1 doceavo de dedo = 1,451 mm.
13 - Análisis del triángulo equilátero según la anchura del óleo de Las Meninas.
Caso Primero, es decir; manteniendo la anchura de 133,625 unidades tendríamos:
133,625 x 2 / √3 = 154,2968594... unidades.
154,2968594... unidades / 1,125 unidades por pulgada = 137,1527639... pulgadas.
137,1527639... pulgadas x 0,02325 metros la pulgada = 3,188801761... metros.
3,188801761... metros correspondería a la altura de Las Meninas.
Caso Segundo, es decir; manteniendo la anchura de 133,5 unidades tendríamos:
133,5 x 2 / √3 = 154,1525218... unidades.
154,1525218... unidades / 1,125 unidades por pulgada = 137,0244639... pulgadas.
137,0244639... pulgadas x 0,02325 metros la pulgada = 3,185818785... metros.
3,185818785... metros correspondería a la altura de Las Meninas.
14 - Boletín del
Museo del Prado. Mayo-agosto 1984. La restauración de Las Meninas
de Velázquez. Manuela B. Mena Marqués.
15 - Ramiro Moya: El trazado regulador y la perspectiva en Las Meninas.
REVISTA ARQUITECTURA.
ÓRGANO DEL COLEGIO OFICIAL DE ARQUITECTOS DE MADRID.
AÑO 3 NUM. 25 - ENERO 1961.
|
|
|
|
16 - Página 202 - Libro IX - I DIECI LIBRI DELL´ARCHITETTURA DI M. VITRVVIO. Tradutti et commentati da Monsignor Barbaro eletto patriarca d'Aquileggia. Venecia. MDLVI.
Hauendo queſto Pithagora ritrouato, non dubitando di non eſſer ſtato in quella inuentone dalle Muſe ammonito riferendole grandisſime gratie ſi dice, che le ſacrificaſſe uittime, & quella ragione come in molte coſe, & in molte miſure è utile, coſi ne gli edificij per fare le ſcale, accioche ſiano i gradi di proportionata miſura, e molto ſpedita, perche ſe l’altezza del Palcho da i capi della trauatura al liuello, & piano da baſſo ſerà in tre parti diuiſa, la ſceſa delle ſcale ſerà cinque parti di quelle con giuſta larghezza de i fuſti, e, tronchi; perche quanto grandi ſeranno le tre parti dalla ſomma trauatura al liuello di ſotto, quattro di quelle ſi hanno à tirare in fuori, & ſcoſtarſi dal dritto, perche coſi moderate ſeranno le impoſte de, i, gradi, & delle ſcale, & ancho di tal coſa la forma ſerà diſſegnata.
Y escribe el español Iuan Perez de Moya en la página 95 - Tratado de Geometria Practica y Speculatiua - Alcala - M. D. LXX. III..
|
|
De otro modo podras prouar ſi es vna eſquadra perfecta. Abre el compas en vna quantidad conueniente, y contando en el vn lado, ò linea de la eſquadra (començando del punto a.) tres tamaños ſemejantes à la diſtancia de la abertura del compas, como en la linea a. c. de la ſiguiente figura denotan las letras d. e. f.
Luego toma en el otro lado, ò linea a. b. quatro tamaños ſemejantes à eſtos como denota g. h. i. k. Saca agora vna linea recta deſde el punto f. haſta el punto k. y ſi eſta linea tuuiere cinco tamaños ſemejantes a los tres que tomaſte en el lado a. c. ò a los quatro del lado a. b. la tal eſquadra ſera verdadera, y ſi ay menos, o mas tamaños de cinco eſtara falſa, como ſe prueua por la penultima del primero de Euclides. Porque ſi el angulo a. es recto, el quadrado de la linea a. f. y a. k. ha de ſer ygual al quadrado de la linea f. k. que es lado opueſto al dicho angulo recto, pues ſi el lado a. f. tiene tres tamaños, y en el a. k. tiene quatro, la ſumma de los quadrados deſtos numeros 3. y 4. es 25. Luego el otro lado f. k. es neceſſario que tenga cinco tamaños, para que ſu quadrado haga veynte y cinco, que es lo que haze la ſumma de los quadrados de los otros lados que comprehenden el angulo recto. Ha ſe dicho eſto aquí porque como con eſte inſtrumento ſe ha de moſtrar medir diſtancias, es bien ſaberle hazer. |
19 - Libro I - Theorema. 33. - Propoſitio. 47.
En los triangulos rectangulos el quadrado que es hecho de el lado que eſta opueſto al angulo recto es ygual a los dos quadrados que ſon hechos de los lados que contienen el angulo recto.
|
|
Sea el triangulo rectangulo .ABC. que tenga recto el angulo BAC. digo que el quadrado que es hecho del lado .EC. es ygual a los quadrados que ſe hazen de .BA. y de .AC. Deſcribaſe, por la .46. de la .BC. el quadrado .BDCE, y por la miſma, de la BA. y de la, AC. los quadrados .ABZI. ACKT. y por el punto A. tireſe .AL. parallela con la .BD. CE, por la propoſicion .31, y por la .I. peticion tireſe AD. CZ. y porque los angulos. BAC. BAI. ſon rectos. Luego tiradas dos lineas rectas .AC. AI. deſde vna linea recta .AB. y deſde vn punto en ella .A. no hacia vnas miſmas partes hacen de vna y otra parte angulos yguales a dos rectos por la .14. propoſition, luego en derecho eſta la .AC. de la .AI y por eſto tambien BA eſta en derecho de .AT y porque el angulo .DBC. es ygual al angulo .ZBA. porque cada vno dellos es recto; pongaſe comun el angulo ABC. Luego todo DBA es ygual a todo el angulo ZBC. y porque las dos .AB. BD. ſon yguales a las dos BZ. BC. la vna a la otra, y el angulo .DBA es ygual al angulo .ZBC. luego la baſis .AD, por la .4. propoſicion, es ygual a la baſis .ZC. y el triangulo .ABD. al triangulo .ZBC. es tambien igual. Y el parallelogramo .BL, por la 41, es doblo del triangulo .ABD porque tiene vna miſma baſis que es .BD. y esta en vnas miſmas parallelas, es a ſaber .DB. AL. y tambien el quadrado .IB. por la miſma, es doblo del triangulo .ZBC. porque tiene la miſma baſis que es .BZ. y eſta en vnas miſmas parallelas, es a ſaber .ZB. IC. y las coſas que ſon doblo de coſas yguales, por la .6. comun ſentencia, entre ſi ſon yguales. Luego el parallelogramo .BL. es ygual al quadrado .IB Semejantemente ſi por .I. peticion, ſe tiran .AE BK. ſe demoſtrara el parallelogramo CL. ſer ygual al quadrado .TC. Luego todo el quadrado .BDEC, es ygual a los dos quadrados .IB, TC. Y el quadrado .BDEC. es hecho de la .BC. y los quadrados IB. CT. ſon hechos de la .BA. AC. Luego el quadrado que de el lado .BC. ſe hizo es ygual a los quadrados que ſon hechos de los lados .BA. AC. luego en los triangulos rectangulos el quadrado que es hecho del lado que eſta oppueſto al angulo recto y lo que mas ſe ſigue como en el theorema, que ſe hauia de demoſtrar. |
| Demostración |
LOS SEIS LIBROS PRIMEROS DE LA GEOMETRIA DE EVCLIDES -
Traduzidos en lengua Eſpañola por Rodrigo Çamorano Aſtrologo y Mathematico, y Cathedratico de Coſmografia por ſu Mageſtad en la caſa de la Contratacion de Seuilla. Dirigidos al illuſtre ſeñor Luciano de Negron, Canonigo de la ſancta ygleſia de Seuilla. Con licencia del Conſejo Real. En Seuilla en caſa de Alonſo
de la Barrera. 1576.
|
La Kabala y Las Meninas |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |