|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fentoni tiene licencia CC BY-NC 4.0 |
|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fentoni tiene licencia CC BY-NC 4.0 |
|
|
La rehabilitación del sistema de
medidas castellanas, y la confianza en un modelo
matemático exacto,
han sido las claves para recuperar el mensaje interno de
Las Meninas.
Si calificásemos a esta pintura como ejemplo de gran invención se deduciría de su autor el fruto y provecho de sus saberes, y que, al igual que Fidias en la escultura, hizo del guarismo la pauta de su estilo naturalista.
El número, como principio omnipresente en el Universo, ordena el arte de Las Meninas.
 |
|
De Diego Velázquez y de Luca Pacioli |
A finales del siglo XV, Luca Pacioli en su libro DE DIVINA PROPORTIONE [1], título que hace referencia a la proporción del número áureo, escribe:
|
De ahí que entre los sabios se acostumbra a decir, según proverbio común: Aurum probatur ignis et ingenium mathematicis, es decir, que la bondad del oro la demuestra el fuego y la calidad de los ingenios las disciplinas matemáticas. Y esta sentencia pretendía expresar que el genio apto para las matemáticas lo es también para las otras ciencias (...).
(...) Platón negaba, no sin razón, la entrada a los que ignorasen la geometría en su celebérrimo gimnasio, sobre cuya puerta principal colocó, en letras grandes y bien inteligibles, una breve inscripción con estas formales palabras: Nemo huc geometriæ expers ingrediatur, es decir, que no entrase quien no fuese un buen geómetra; e hizo esto porque en la geometría se encuentra oculta toda otra ciencia. |
A pesar de que Velázquez confirme en esta obra de arte su interés por todo tipo de efecto lumínico, la finalidad de esta investigación es establecer la diferencia entre la imagen pintada del natural y la de aquella otra suscitada de la observación.
|
|
|
|
La Puerta semiabierta de cuarterones abre paso hacia una pared lejana, y a una Geometría donde se oculta toda otra ciencia, como así señaló Luca Pacioli, y Diego Velázquez expresó a la española.
En este área de Las Meninas la presencia de uno de los diez Sefirot de la Kabala, la Sefira número siete, situada ante el retrato de la menina Isabel de Velasco y la silueta del Aposentador José Nieto, custodia la efigie del protagonista más importante de la tradición cabalística [2].
Señalaremos, pues, donde se encuentran en este óleo estas pinceladas tan especiales:
|
|
UNOS CABELLOS QUE REPRESENTAN A UN ROSTRO
En el pelo de la menina Isabel de Velasco se descubre, pues, la presencia de un profeta, que, de manera explícita, corresponde al rostro de Moisés, y, sin entrar en detalles, sugeriríamos; que los dos adornos esbozados en su parte superior simbolizarían las dos tablas de la ley.
|
|
El patriarca Moisés
Este nuevo personaje comparte con esta menina la posición de su oreja, tiene apariencia masculina, de tez morena y avanzada edad, poblada barba agrisada, de aspecto bíblico, mira hacia la luz que entra por la ventana de la derecha, tiene cara de suplicar y de estar en trance a la par, los toques de pintura blanca y oscura, además de ser texturados como pelos, son elementos caligráficos hebraicos. |
|
|
|
Descubrimos, pues, un oscuro secreto camuflado en la misma textura del pelo de la menina Isabel de Velasco, que habla de Teología, una disciplina también conocida como la ciencia de Dios, y que quizás este fuera el motivo por el que Luca Giordano calificara a Las Meninas como la Teología de la pintura en presencia del rey Carlos II.
Ya que los antiguos cabalistas asociaron los patriarcas bíblicos con las esferas del Árbol de la Vida según su naturaleza, conocemos, a ciencia cierta, la identidad del personaje masculino consolidado en la cabeza de la menina que analizamos porque Moisés, autor de la Torah y líder indiscutible de la Kabala, quedó afianzado, pues, al pie de la columna derecha.
En 1550 Petri Galatini presenta el trabajo de Ioannis Reuchlini Phoroensis, Doctoris de Arte Cabalistica, en su libro de Opus de Arcanis Catholicæ Veritatis impreso en BASILEÆ, y explica en la página nº 851, Libri tres, los atributos de la séptima Sefira en estos términos:
|
Ad ſeptimam referuntur, Adonai Sabaoth, crus, pes, columna dextera, rota magna, uiſio prophetiæ, Moyſes & cætera.
Al séptimo se refieren a; Adonai Sabaoth, la pierna, el pie, la columna derecha, la gran rueda, la visión de la profecía, Moisés y otros. |
Y un siglo después, Athanasius Kircher secunda en latín los mismos contenidos simbólicos que se ocultan tras el retrato de la menina Isabel de Velasco, en la séptima Sefira, Nectzah, La Victoria:
|
7 נצח Netſah Victoria, Æternitas |
Septimum veſtimentum Dei ſeu Sephirah dicitur נצח Netſah, id eſt, triumphus, victoria, ſeu æternitas, cui nomen יהוה צבאות Adonai Tſebaoth. Eius attributa ſunt, Crus, pes, columna dextera, rota magna, viſio Prophetæ. Canalis eſt, per quem Deus influit in Principatus, & per Intelligentiam Haniel in Cœlum Veneris. Plantarum cauſa & origo eſt. |
|
|
|
7 נצח Netzach Victoria, Eternidad |
La séptima vestidura de Dios es la Sefira denominada el Triunfo, Victoria o Eternidad, es decir; Netzach, cuyo nombre es יהוה צבאות, Adonai Tsebaoth. Sus atributos son: la pierna, el pie, la columna derecha, la gran rueda, la visión del Profeta. Netzach es el canal a través del cual Dios fluye hacia los Principados, y, a través de la Inteligencia de Haniel, hacia el Cielo de Venus. Es la causa y el origen de las plantas. |
|
CLASSIS IV. CABALA HEBRÆRVM - CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI. Tomus Secundus. GYMNASIVM. ROMÆ - Anno M DC LIII. |
En definitiva, un retrato primoroso de gran arraigo salomónico:
רֹאשׁוֹ, כֶּתֶם פָּז; קְוֻצּוֹתָיו, תַּלְתַּלִּים, שְׁחֹרוֹת, כָּעוֹרֵב׃
Su cabeza es un tesoro de oro fino, sus mechones le cuelgan, negros como el cuervo.
Cantar de los Cantares 5:11
Sabemos, pues, que la mística desvelada en Las Meninas es heterodoxa, y tanto aquellos que conozcan el tipo de creencia que tratamos, como los que nunca han oído hablar de ella, mudan en testigos encandilados ante esta exhumación artística velazqueña.
Y conmueve contemplar, por primera vez en la vida, la inusitada imagen de Moisés en el pelo de la menina Isabel de Velasco, que, como profeta, niega el dilema, y persuade hondamente al espectador.
|
|
|
|
La tradición oral hebrea se valió de la boca y del oído para guardar fuera de la vista a la Kabala, y, en esta ocasión, sin menoscabo alguno, ha sido el ojo testigo de Su fehaciente presencia en las pinceladas de luz y color de esta pintura.
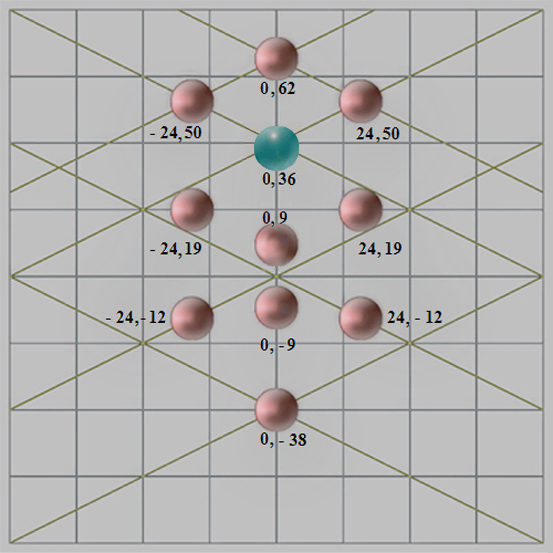 |
Numeración |
Hebreo |
Castellano |
Planeta |
Abscisas - X |
Ordenadas - Y |
|
I |
Kether |
Corona |
0 |
62 | ||
|
II |
Chokmah |
Sabiduría |
24 |
50 | ||
|
III |
Binah |
Inteligencia |
Saturno |
- 24 |
50 | |
|
Dahat |
Conocimiento |
0 |
36 | |||
|
IV |
Chesed |
Merced o Gracia |
Júpiter |
24 |
19 | |
|
V |
Geburah |
Fortaleza |
Marte |
- 24 |
19 | |
|
VI |
Tipheret |
Hermosura |
Sol |
0 |
9 | |
|
VII |
Netzach |
Eternidad o Vitoria |
Venus |
24 |
- 12 | |
|
VIII |
Hod |
Alabanza o Confisión |
Mercurio |
- 24 |
- 12 | |
|
IX |
Yesod |
Fundamento |
Luna |
0 |
- 9 | |
|
X |
Malkut |
Reino |
Tierra |
0 |
- 38 |
|
|
Los diez Sefirot, simbolizados en nuestro mundo físico a través del Árbol de la Vida, han representado, desde siempre, una imagen metafórica del descenso de la divinidad, o, a la inversa, del camino ascendente para alcanzar el estado de consciencia espiritual.
No obstante, la percepción de estas Esferas oscila entre la certeza de Su inmaterialidad y la finalidad del mensaje de Las Meninas.
 |
|
|
No hay nada en estas esferas que no presuma ser la percepción de un legado sagrado, hablamos, pues, de diez esferas + una que enaltecen el acto social pintado por Velázquez, y convocan una entidad subyacente denominada:
El Rostro místico de Dios.
Sacamos en conclusión, pues, que ante esta circunstancia, la familia real española demandaba más que ayuda en el año 1656.
|
Otros, de quien hace mencion el P. Benito Pereyra en el libro primero de su Comento sobre el Genesis, discurriendo que desde la venida de Christo hasta el fin del mundo, correria igual espacio de tiempo, que desde la Creacion hasta el Diluvio, pronosticaban la ruina del Orbe para el año 1656 de nuestra Redencion [3]. |
Una Profecía bíblica, a la cual temer, en pugna con el orden planetario, y que hacía alusión, ni más ni menos, al año 1656, el mismo año en el que fueron pintadas Las Meninas.
La Geometría del espacio aéreo de Las Meninas se manifiesta simbólica a través de los 10 Sefirot + Dahat, y, de igual suerte, que a finales del Siglo XV, en un retrato anónimo de Luca Pacioli, se representa un poliedro colgado de un cordel en una obra que se exhibe en el Museo de Capodimonte de Nápoles desde el año 1957.
|
|
Kepler llamó a este poliedro el rhombicuboctahedron. |
Ya que en esta época se consideraba a la Aritmética y Geometría el fundamento del Arte liberal de la Matemática, un pintor de la categoría de Velázquez, que anhelaba abrir las puertas de la Escuela de Platón, tuvo la oportunidad de ampliar sus conocimientos en la Academia de Matemática de Madrid [4].
Miguel Geronimo de Santa Cruz rememora su hallazgo de esta manera [5]:
|
La Practica de Aritmética, como afirma Juan de Sacrovoſco, fue dada compedioſa en luz de vn Filoſofo llamado Algo, y por aqueſta cauſa fue llamado el Guariſmo. |
La Aritmética que estudió Velázquez se componía de cinco reglas o guariſmos principales:
|
No ſe han de contentar los hombres con ſolamente ſaber las dichas cinco reglas principales, aunque con ellas ſe practican todas las quentas del mundo, mas es meneſter ſaberſe aprovechar de ellas, y aplicarlas donde fuere meneſter, cada vna en ſu caso, y lugar, y ſaber obrar con ellas las reduciones de las monedas, y de los quebrados, y como ſe ha de hazer vna regla de tres, ó vna regla de compañias, y las demás queſtiones, que ſe ſuelen ofrecer en el Arte mercancial, y en otras Artes; porque ſi no ſaben la practica, ni vſar de las dichas cinco reglas, podré comparar las tales, que le ſirven al Contador, como las colores, y matizes al Pintor, las quales colores no baſta ſaberlas hazer, ni tenerlas diſtintas en los vaſos, y conchas, ſino que ha de ſaber hazer vna figura, ó imagen, practicando con artificio la pintura que quiere pintar, aplicando para cada coſa, las colores convenientes, é irlas aſſentando con ſu pincel, y ſaberse aver con ellas, para pintar vnos lexos, ó vn arbol, ó lo que ſe le ofrece; y ſi no ſupieſſe el Arte de pintar, ó la proſpectiva, poco aprovechará ſaber hazer las colores; mas ſabiendo lo vno, y lo otro, ſería Pintor perfecto; y aſsí el que no deprendiere mas de las cinco reglas principales de quentas, gozará de la flor, y no del fruto, ni del fin que pretende, y ſi lo consiguiere, ſerá con mucho trabajo, y raras vezes. |
La Vara Real
de Burgos
en la época de la construcción del Monasterio del Escorial estandarizó el
sistema de medidas en todos los reinos de España; y
así lo confirma
la
pragmática dictada por el monarca Felipe II el 24 de junio de 1568
[6]:
Y declaramos que la vara Caſtellana de que se ha de uſar en todos eſtos Reynos, ſea la que hay y tiene la ciudad de Burgos.
|
GEOMETRÍA DE LA VARA CASTELLANA
|
La Vara, para medir los texidos, tiene 3 pies Burgaleses, 4 palmos, 36 pulgadas, ó 48 dedos. También se divide en tercia, sesma, octava ó media quarta, y 16 avos ó media octava.
El Pie que sirve á medir madera y otros cuerpos, se llama Pie Burgalés, por ser Burgos donde se halla el Padrón original de la Vara Castellana, cuya tercia parte hace un pie. Este se divide en 12 pulgadas, y cada pulgada en doce líneas; de suerte, que el pie tiene 144 líneas, y la vara 432 [7]. |
En el fresco de Pellegrino Tibaldi de la biblioteca del Monasterio del Escorial se representa a Salomón resolviendo los enigmas que le ha planteado la Reina de Saba, no obstante, la legendaria sabiduría que personifica este rey bíblico alude, pues, al alter ego del rey Prudente Felipe II.
|
|
OMNIA IN NUMERO, PONDERE ET MESURA
TODO TIENE NÚMERO, PESO Y MEDIDA |
|
|
En el lateral del tapete carmín de la mesa está escrita una frase en hebreo que recalca la importancia del sistema de pesos y medidas, y, en particular, sobre la mesa, destaca, pues, la Vara Real de Burgos, que Felipe II en 1568 estandarizó para promover la uniformidad en las medidas utilizadas en la construcción del Monasterio del Escorial y en sus dominios:
Tenemos bien sabido que la vara Castellana equivale a tres pies, el pie a doce pulgadas, la pulgada castellana se compone de doce partes iguales llamadas líneas, y que la línea se divide en 12 puntos, no obstante, y sin contrariar al sistema de medidas castellano, podríamos ya adelantar que Velázquez fracciona a la pulgada en 9 partes iguales para poder operar con la unidad en sus precisas operaciones:
8/9 de pulgada equivale a la unidad en la rejilla de trabajo.
Hablamos, pues, de una proporción en la que ocho partes de nueve equivalen a la unidad, lo cual nos recuerda que en música un intervalo más su inversión siempre suman una 9ª, por lo que la inversión del intervalo de una 8ª sería el unísono.
| unidades | valor decimal | nota musical | armonía | |
| 9/8 | = | 1,125 | Re | Tono fundamental |
| 8/8 | = | 1 | Do | Unísono |
| 7/8 | = | 0,875 | División proporcional | |
| 6/8 | = | 0,75 | Fa | Proporción de 4ª justa |
| 5/8 | = | 0,625 | División proporcional | |
| 4/8 | = | 0,5 | Do | 1ª octava descendente |
| 3/8 | = | 0,375 | División proporcional | |
| 2/8 | = | 0,25 | Do | 2ª octava descendente |
| 1/8 | = | 0,125 | Do | 3ª octava descendente |
Al integrar la armonía pitagórica en la métrica de la pulgada castellana, se demuestra que la estructura de Las Meninas se basa en la antigua filosofía de la Música Universalis, es decir; la música de las esferas, donde las proporciones matemáticas rigen tanto el arte como la música.
Mostramos, pues, tres conceptos clave unificados de un sistema de proporciones complejo:
Matemáticas; se muestra la división de la unidad en octavos y sus valores decimales exactos.
Música; estas fracciones se relacionan con notas musicales y términos de armonía como el tono pitagórico y el unísono.
Proporción; y se demuestra que las relaciones numéricas que rigen la armonía musical pueden aplicarse a las unidades de medida en la Geometría.
Algunas fracciones de esta tabla, aunque matemáticamente consistentes, sus valores no corresponden a una nota musical reconocible, sin embargo, la división en nueve partes de la pulgada castellana es, de hecho, una inversión armónica que permite la perfecta integración de la Geometría con la Música.
La división platónica del Alma del Mundo revela su conexión con las consonancias musicales y las proporciones, donde la razón epogdoica, 9/8, es el origen del tono entero, y, aunque no sea una consonancia en sí misma, constituye, pues, el principio de las consonancias que permite el movimiento proporcional según las armonías musicales.
Al Tono pitagórico le corresponde, pues, la proporción sesquioctava 9/8, es decir; el ratio entre la quinta y la cuarta:
3/2 ÷ 4/3 = 9/8 = 1,125.
| INTERVALO | PROPORCIÓN | RATIO | Valor decimal | |
| Quinta | sesquiáltera | 3/2 | = | 1,5 |
| Cuarta - Justa | sesquitercia | 4/3 | = | 1,333333... |
| Tercera mayor - Justa | sesquicuarta | 5/4 | = | 1,25 |
| Tono mayor | sesquioctava | 9/8 | = | 1,125 |
| Tono menor | sesquinona | 10/9 | = | 1,111111... |
| Inversión del Tono mayor | inversión | 8/9 | = | 0,888888... |
|
Sectio canonis - Euclides |
Sesqui, una voz y media, es un prefijo dado en la música mensural de los siglos XV y XVI a las proporciones cuyo numerador es mayor en una unidad al denominador.
De modo, que, a partir de LA UNIDAD, quedan conectados, en una misma arquitectura metrológica, conocimientos de distintas disciplinas del saber que comparten, pues, el lenguaje matemático de la Geometría Sagrada en la Medida del Arte y la Música.
No obstante, consideraremos la aplicación práctica de la teoría musical por el maestro Velázquez en el formato de la Túnica de José, cuyos sonidos armónicos Pitágoras descubrió en el repicar de unos martillos batiendo un yunque.
 |
 |
|
|
| Autor |
Medidas del Catálogo |
Reajuste |
Sistema castellano |
Ratio |
|
Diego Velázquez |
2,84 x 2,135 metros |
2,841666... x 2,13125 metros |
122 y
2/9
x 91 y 6/9 pulgadas |
4/3 |
|
|
La relación del ancho y el alto de las dimensiones de este óleo es exactamente de 4/3, que corresponde a la proporción la cuarta justa, uno de los intervalos más consonantes en la Música, lo que demuestra que este hallazgo es la evidencia concreta de que las medidas de La Túnica de José fueron cuidadosamente elegidas para encajar en un sistema de proporción, que, al igual que en Las Meninas, Velázquez aplicó como un principio de orden para crear una composición visualmente equilibrada, reforzando la idea de que su arte y la música estaban entrelazados por una misma arquitectura matemática.
En esta búsqueda habría que señalar que la conversión
tradicional de la pulgada castellana al sistema métrico provoca una pequeña
diferencia respecto al tamaño de LA UNIDAD con la que operamos, y este desfase
es perceptible debido a que Velázquez no solo construyó su obra
con Matemática, sino que la perfeccionó utilizando números
enteros y racionales, y sus equivalentes en el sistema de medidas
castellano, para la salvaguardia del cálculo
aritmético.
0,279 - 0,278635 = 0,000365 metros, es decir; una diferencia de 365 micrómetros.
Y, en consecuencia, este leve margen, del sistema de unidades que utilizamos respecto al tamaño tradicional asignado al pie castellano, determina, pues, la diferencia entre lo justamente razonable y el desbarajuste de conversión actual entre el sistema castellano y el metro francés.
La precisión de LA UNIDAD marca la diferencia entre la adaptación matemática de este nuevo sistema, y la incertidumbre en las mediciones físicas con sistemas históricos convencionales.
1 Pulgada = 0,279 metros / 12 = 0,02325 metros.
|
En la siguiente tabla se plasma la equivalencia entre el valor de la pulgada castellana y las unidades; lo cual indica que nos hallamos ante la cuantía de 1,125 unidades por pulgada, o número conversor, que traduce las pulgadas castellanas en cualquier clase de sistema de medidas longitudinales, y que, con extrema exactitud, además nos pone en relación con las dimensiones reales de Las Meninas. |
| 9 partes | Unidades | La Pulgada en 9 partes | Pulgadas | Milímetros | ||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 |
| 8/8 | = | 1 | 8/9 | = | 0,888888 | 20,666666 |
| 7/8 | = | 0,875 | 7/9 | = | 0,777777 | 18,083333 |
| 6/8 | = | 0,75 | 6/9 | = | 0,666666 | 15,5 |
| 5/8 | = | 0,625 | 5/9 | = | 0,555555 | 12,916666 |
| 4/8 | = | 0,5 | 4/9 | = | 0,444444 | 10,333333 |
| 3/8 | = | 0,375 | 3/9 | = | 0,333333 | 7,75 |
| 2/8 | = | 0,25 | 2/9 | = | 0,222222 | 5,166666 |
| 1/8 | = | 0,125 | 1/9 | = | 0,111111 | 2,583333 |
|
|
| UNIDAD | PULGADA | MILÍMETRO |
|
La pulgada dividida en nueve fracciones, que llamamos la división velazqueña, está en relación directa con cada una de las 12 líneas en las que se divide la pulgada castellana a través de las cantidades 3 y 4; números correspondientes al tamaño de los catetos del triángulo pitagórico o escuadra perfecta. |
| la división velazqueña | la pulgada castellana |
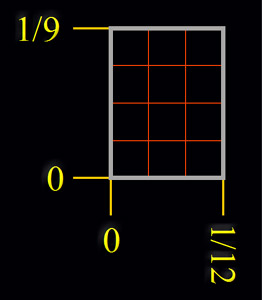 |
| 1/9 = 16 puntos | 1/12 = 12 puntos | |
| 4 partes × 9 = 36 partes | 3 partes × 12 = 36 partes | |
| 9 fracciones | 12 fracciones | |
| 1/9 ≈ 23,25/9 = 2,583333 milímetros | 1/12 ≈ 23,25/12 = 1,9375 milímetros |
Será, por tanto, la unidad la que garantice en Las Meninas una Aritmética y Geometría exacta, a lo que se sumaría, su puesta en práctica al escalar el tamaño real pintado de la pared del fondo, y el perfecto anidamiento del escenario velazqueño en los siguientes formatos:
FORMATO 8
| Formato | Proporción | Pulgadas por unidad | Anchura | Tamaño en metros | ||||
| 8 | 8/9 | 0,888888 | × | 72 unidades | = | 64 pulgadas | 8 × 8 × 0,02325 = 1,488 metros | |
|
|
| formato | proporción | escala | unidades | pulgadas | metros | |||
| 8 | 8/9 | = | 0,888888 | × | 72 | = | 64 | 8 × 8 × 0,02325 = 1,488 |
| 7 | 7/9 | = | 0,777777 | × | 72 | = | 56 | 7 × 8 × 0,02325 = 1,302 |
| 6 | 6/9 | = | 0,666666 | × | 72 | = | 48 | 6 × 8 × 0,02325 = 1,116 |
| 5 | 5/9 | = | 0,555555 | × | 72 | = | 40 | 5 × 8 × 0,02325 = 0,93 |
| 4 | 4/9 | = | 0,444444 | × | 72 | = | 32 | 4 × 8 × 0,02325 = 0,744 |
| 3 | 3/9 | = | 0,333333 | × | 72 | = | 24 | 3 × 8 × 0,02325 = 0,558 |
| 2 | 2/9 | = | 0,222222 | × | 72 | = | 16 | 2 × 8 × 0,02325 = 0,372 |
| 1 | 1/9 | = | 0,111111 | × | 72 | = | 8 | 1 × 8 × 0,02325 = 0,186 |
| 0 | 0/9 | = | 0,000000 | × | 72 | = | 0 | 0 × 8 × 0,02325 = 0 |
|
|
|
|
|
|
| Formato | Proporción | Pulgadas por unidad | Altura | Tamaño en metros | ||||
| 8 | 8/9 | 0,888888 | × | 60 unidades | = | 53 y 1/3 pulgadas | 8 × 6,666 × 0,02325 = 1,24 metros | |
|
|
| formato | proporción | escala | unidades | pulgadas | metros | |||
| 8 | 8/9 | = | 0,888888 | × | 60 | = | 53 y 1/3 | 8 × 6,666 × 0,02325 = 1,24 |
| 7 | 7/9 | = | 0,777777 | × | 60 | = | 46 y 2/3 | 7 × 6,666 × 0,02325 = 1,085 |
| 6 | 6/9 | = | 0,666666 | × | 60 | = | 40 | 6 × 6,666 × 0,02325 = 0,93 |
| 5 | 5/9 | = | 0,555555 | × | 60 | = | 33 y 1/3 | 5 × 6,666 × 0,02325 = 0,775 |
| 4 | 4/9 | = | 0,444444 | × | 60 | = | 26 y 2/3 | 4 × 6,666 × 0,02325 = 0,62 |
| 3 | 3/9 | = | 0,333333 | × | 60 | = | 20 | 3 × 6,666 × 0,02325 = 0,465 |
| 2 | 2/9 | = | 0,222222 | × | 60 | = | 13 y 1/3 | 2 × 6,666 × 0,02325 = 0,304 |
| 1 | 1/9 | = | 0,111111 | × | 60 | = | 6 y 2/3 | 1 × 6,666 × 0,02325 = 0,155 |
| 0 | 0/9 | = | 0,000000 | × | 60 | = | 0 | 0 × 6,666 × 0,02325 = 0 |
|
|
Si
una pulgada se divide en doce partes iguales llamadas doce
líneas, entonces,
la división
velazqueña, fraccionada en nueve partes, equivaldría a
la misma pulgada castellana de 23,25 milímetros, pero
en consonancia con el sistema de medidas implementado en el lienzo de Las Meninas.
El Pie Real equivale a 12 pulgadas, y mide 0,279 metros.
1 Pulgada = 0,279 metros / 12 = 0,02325 metros.
| 36 partes | Unidades | La Pulgada de 12 líneas | Pulgadas | Milímetros | ||
| 36/32 | = | 1,125 | 12/12 | = | 1 | 23,25 |
| 33/32 | = | 1,03125 | 11/12 | = | 0,916666 | 21,3125 |
| 30/32 | = | 0,9375 | 10/12 | = | 0,833333 | 19,375 |
| 27/32 | = | 0,84375 | 9/12 | = | 0,75 | 17,4375 |
| 24/32 | = | 0,75 | 8/12 | = | 0,666666 | 15,5 |
| 21/32 | = | 0,65625 | 7/12 | = | 0,583333 | 13,5625 |
| 18/32 | = | 0,5625 | 6/12 | = | 0,5 | 11,625 |
| 15/32 | = | 0,46875 | 5/12 | = | 0,416666 | 9,6875 |
| 12/32 | = | 0,375 | 4/12 | = | 0,333333 | 7,75 |
| 9/32 | = | 0,28125 | 3/12 | = | 0,25 | 5,8125 |
| 6/32 | = | 0,1875 | 2/12 | = | 0,166666 | 3,875 |
| 3/32 | = | 0,09375 | 1/12 | = | 0,083333 | 1,9375 |
|
|
| UNIDAD | PULGADA | MILÍMETRO |
Y en el siguiente paso reconoceremos, pues, la precisión del sistema de medición usado en todo momento de este análisis.
La exactitud es la capacidad de un instrumento para medir un valor cercano a la magnitud real.
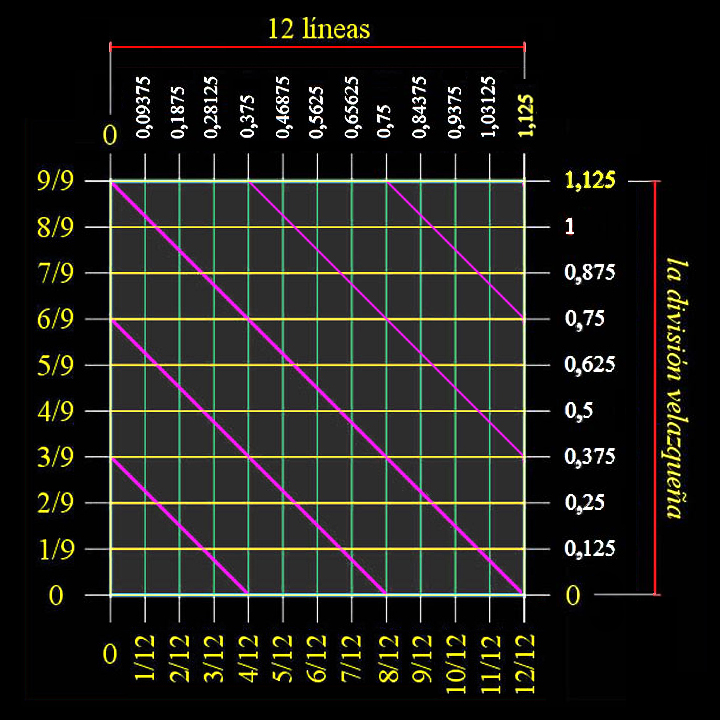 |
|
|
El cálculo de la profundidad
Caso aparte es la división de la pulgada
castellana en consonancia con la profundidad
de Las Meninas, es decir; con
el tamaño real de la pared del fondo medida en la distancia.
FORMATO 30
| Formato | Proporción | Pulgadas por unidad | Anchura | Tamaño en metros | ||||
| 30 | 30/9 | = | 3,333333 | x | 72 unidades | = | 240 pulgadas | 30 x 8 x 0,02325 = 5,58 metros |
|
|
| Formato | Proporción | Pulgadas por unidad | Altura | Tamaño en metros | ||||
| 30 | 30/9 | = | 3,333333 | x | 60 unidades | = | 200 pulgadas | 30 x 6,6 x 0,02325 = 4,65 metros |
|
|
 |
La anchura
Tamaño en unidades: 1,125 unidades por pulgada x 64 pulgadas = 72 unidades.
La altura
Tamaño en unidades: 1,125 unidades por pulgada x 53 pulgadas y 1/3 = 60 unidades. |
|
|
Se entiende, pues, que la escala de representación de la pared del fondo de Las Meninas es de: 1/3,75 = 0,266666...
| 45 partes | Unidades | La Pulgada en 15 partes | Pulgadas | Milímetros | Pulgadas reales | ||
| 45/40 | = | 1,125 | 15/15 | = | 1 | 23,25 | 3,75 |
| 42/40 | = | 1,05 | 14/15 | = | 0,933333 | 21,7 | 3,5 |
| 39/40 | = | 0,975 | 13/15 | = | 0,866666 | 20,15 | 3,25 |
| 36/40 | = | 0,9 | 12/15 | = | 0,8 | 18,6 | 3 |
| 33/40 | = | 0,825 | 11/15 | = | 0,733333 | 17,05 | 2,75 |
| 30/40 | = | 0,75 | 10/15 | = | 0,666666 | 15,5 | 2,5 |
| 27/40 | = | 0,675 | 9/15 | = | 0,6 | 13,95 | 2,25 |
| 24/40 | = | 0,6 | 8/15 | = | 0,533333 | 12,4 | 2 |
| 21/40 | = | 0,525 | 7/15 | = | 0,466666 | 10,85 | 1,75 |
| 18/40 | = | 0,45 | 6/15 | = | 0,4 | 9,3 | 1,5 |
| 15/40 | = | 0,375 | 5/15 | = | 0,333333 | 7,75 | 1,25 |
| 12/40 | = | 0,3 | 4/15 | = | 0,266666 | 6,2 | 1 |
| 9/40 | = | 0,225 | 3/15 | = | 0,2 | 4,65 | 0,75 |
| 6/40 | = | 0,15 | 2/15 | = | 0,133333 | 3,1 | 0,5 |
| 3/40 | = | 0,075 | 1/15 | = | 0,066666 | 1,55 | 0,25 |
|
|
| UNIDAD | PULGADA | MILÍMETRO |
En consonancia con la profundidad, La pulgada Castellana queda dividida en 15 partes iguales en la rejilla de trabajo para el cálculo de los tamaños de los distintos elementos situados en la pared del fondo.
RAZONAMIENTO
La
escala de representación de la pared del fondo de Las Meninas
es de: 1/3,75 =
0,266666...
El tamaño real de cualquier elemento de la pared del fondo de Las Meninas se puede averiguar multiplicando la medición en la rejilla de trabajo por la constante 3,333333… pulgadas por unidad.
3,333333… pulgadas por unidad representa un valor de tipo permanente, al menos dentro del contexto o situación para el cual ha sido planeado.
Esa comprobación sólo será válida para los casos concretos que se comprueben.
Es decir; en todos los casos que hablemos del tamaño real de la pared del fondo de Las Meninas de Velázquez.
Nos serviremos de un ejemplo para explicar cómo funcionan estos números:
| Unidades en la pared del fondo | Ratio de ampliación | Medidas reales en pulgadas | ||
| 1,125 | x | 3,333333… | = | 3,75 |
Tomemos, en la columna de las unidades, la cantidad de 1,125, y ahora multipliquemos 1,125 unidades por 3,333333… pulgadas por unidad, el resultado se reflejará en la columna denominada:
Medidas reales en pulgadas, cierto, la solución es la esperada; 3,75 pulgadas castellanas.
Añadimos:
0,3 unidades en la rejilla de medición equivalen en el mundo real de la pared del fondo a:
0,3 unidades x 3,333333... pulgadas por unidad = 1 pulgada = 23,25 milímetros.
|
Unidades sobre la rejilla de trabajo |
Pulgadas sobre la pared del fondo |
Milímetros |
|
1,125 |
3,75 |
87,1875 |
|
1 |
3,333333 |
77,5 |
|
0,3 |
1 |
23,25 |
|
|
Unos números, pues, que se ajustan, con calidad científica, a la apertura del ángulo visual de Las Meninas en el acto espontáneo de mirar.
|
La pulgada dividida en quince fracciones también está en relación directa con cada una de las 12 líneas en las que se divide la pulgada castellana a través de las cantidades 4 y 5. |
| división en quince fracciones | la pulgada castellana |
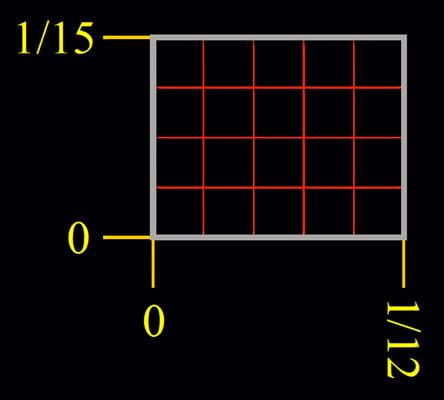 |
| 1/15 = 9,6 puntos | 1/12 = 12 puntos | |
| 4 partes x 15 = 60 partes | 5 partes x 12 = 60 partes | |
| 15 fracciones | 12 fracciones | |
| 1/15 ≈ 23,25/15 = 1,55 milímetros | 1/12 ≈ 23,25/12 = 1,9375 milímetros |
El tamaño geométrico
Entendemos que para documentar
sin
errores el tamaño de
Las Meninas se
requiere, pues, la ayuda auxiliar de la Geometría y del
Cálculo numérico de acuerdo con el
antiguo sistema de medidas castellano.
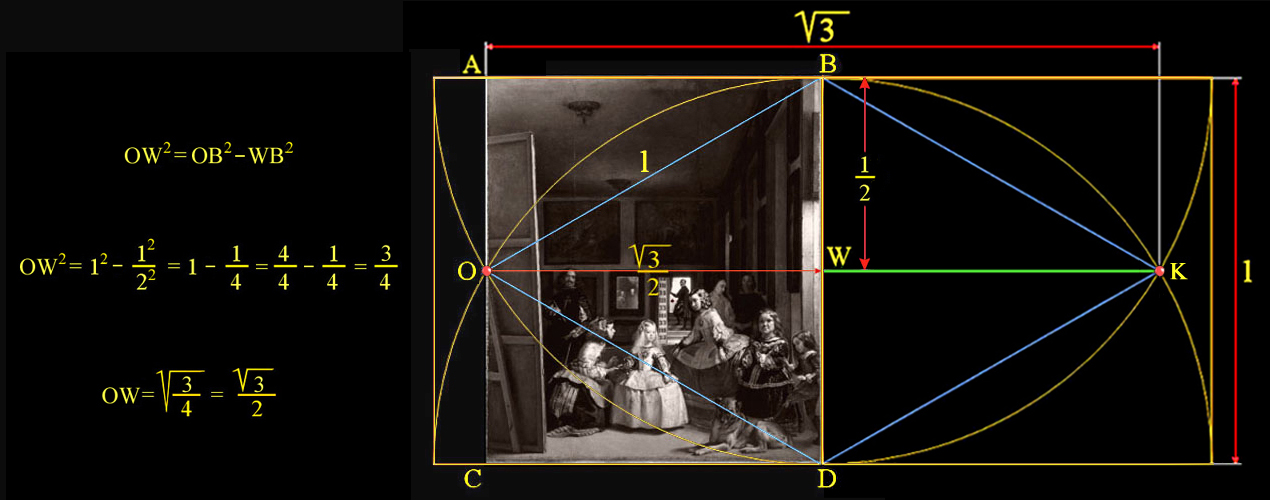 |
|
|
Entendido el desarrollo pitagórico de la anchura del lienzo de Las Meninas en base a un cuadrado, lo completaremos, pues, con el estudio geométrico del tamaño real del lienzo.
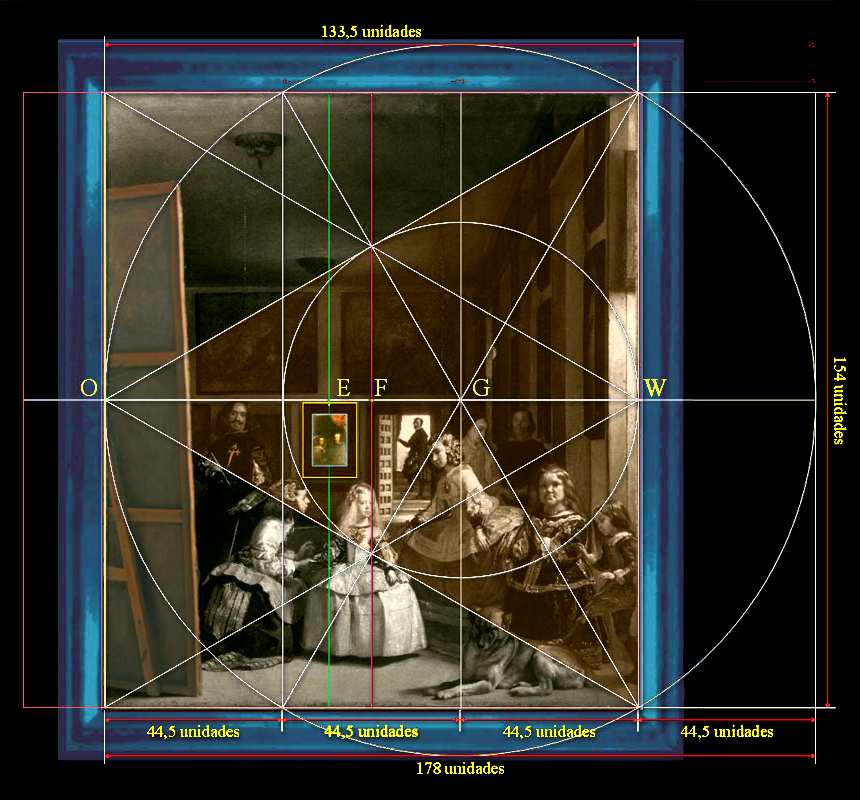 |
|
|
| Tamaño | Unidades | Sistema castellano | Sistema métrico | Museo del Prado |
| Anchura | 133,5 | 118 pulgadas y 6/9 | 2,759 metros | 2,76 metros |
| Altura | 154 | 136 pulgadas y 8/9 | 3,182666 metros | 3,18 metros |
Este gran triángulo, BOD, tiene una altura, OW, de 133,5 unidades, y su base, BD, mide 154 unidades, y si quisiéramos convertirlo en un triángulo equilátero, manteniendo su base de 154 unidades, entonces, la altura, OW, de este gran nuevo triángulo equilátero sería:
OW = √3 ÷ 2 × 154 unidades ≈ 77√3 ≈ 133,367912... unidades
Cuyo resultado es un valor muy cercano a la altura, OW, del triángulo isósceles original de 133,5 unidades de altura.
| Unidad |
Pulgadas |
Milímetros |
|
0,132087... |
0,117410... |
2,729798... |
|
|
Son 2,729798... milímetros de menos, en la altura, OW, de 133,5 unidades, la cantidad exacta para que hablemos, pues, de un triángulo equilátero.
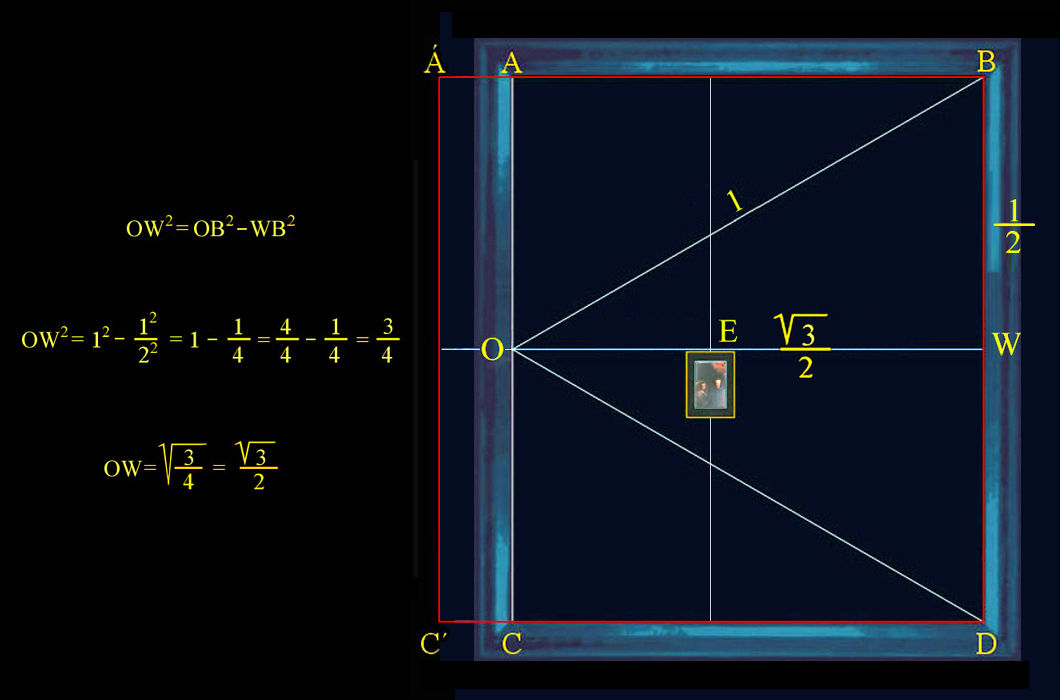 |
|
|
Geometría del Espejo
Habría que considerar ciertas pautas para el cálculo numérico
[8]:
El Pie Real equivale a 12 pulgadas.
La pulgada castellana se divide en 12 líneas.
A la pulgada la hemos fraccionado en 9 partes iguales para operar con la unidad en la rejilla de trabajo.
Asimismo; la medición del tamaño real de la pared del fondo se establece fraccionando a la pulgada castellana en 15 partes iguales en la rejilla de trabajo.
Básicamente, estas cuatro normas dan paso al proceso de medir cualquier esquina de Las Meninas con realidad, profundidad y exactitud [9].
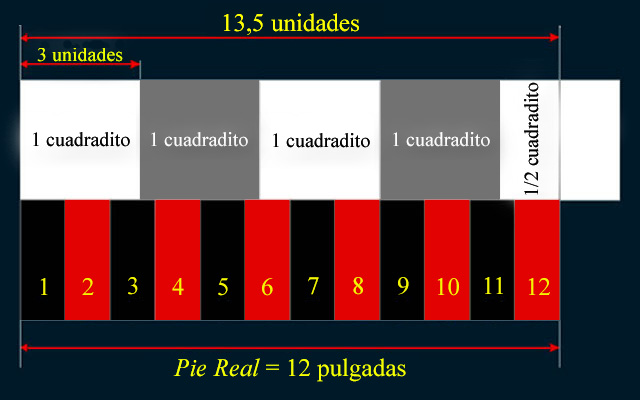 |
|
|
|
Si una pulgada equivale a 1,125 unidades en la cuadrícula de trabajo, entonces; sólo hay que multiplicar 1,125 unidades por 12 para obtener 13,5 unidades, que es la cantidad que representa en esta misma cuadrícula 4,5 cuadraditos valiendo el Pie Real 12 pulgadas. |
Y, como no podría ser de otra manera, será en la misma anchura del espejo de Las Meninas en donde Velázquez proponga la regia medida del Pie Real.
|
|
|
|
El Pie Real, el legítimo patrón de medidas castellano, ejerce el control absoluto sobre las medidas de este lienzo, y quedó puntualmente representado, sin duda, en la anchura del Marco del Espejo.
Pero veamos la operación del cálculo directo del tamaño real del Espejo sabiendo, pues, que la anchura del Marco del Espejo mide 13,5 unidades.
Esta operación del cálculo: 13,5 unidades x 3,333333... pulgadas por unidad = 44,999999... pulgadas, corresponderían, pues. a pulgadas reales.
En el sistema castellano tendríamos:
1,04625 metros / 0,02325 metros por pulgada = 45 pulgadas.
Velázquez dividió las 45 pulgadas de la anchura real del Marco del Espejo entre 3,333333... pulgadas por unidad, y así representar su tamaño de acorde a la distancia:
45 pulgadas / 3,333333... pulgadas por unidad = 13,5 unidades.
|
|
|
|
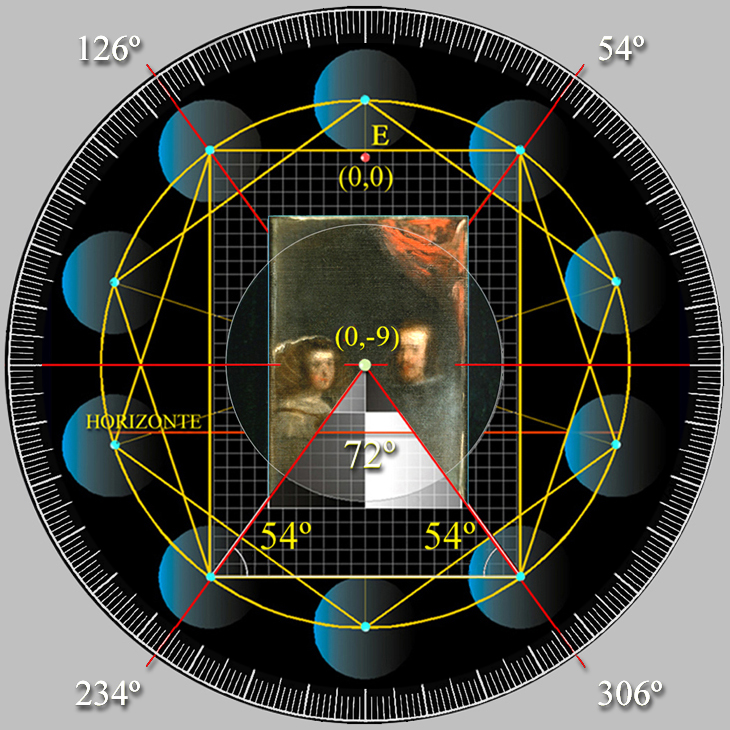
Ya sabemos cómo funciona en la distancia el tamaño real de la anchura del Espejo, pero, para su construcción, habría que considerar que el tamaño de 12 pulgadas de su anchura pertenecen, pues, al tamaño del lado de un Pentágono regular, de modo, que Velázquez fijó, en cuatro de los diez vértices de un decágono, formado por dos pentágonos superpuestos, las cuatro esquina del marco del Espejo, que determinaron el formato del ancho y alto del marco de madera del Espejo de Las Meninas.
 |
 |
|
|
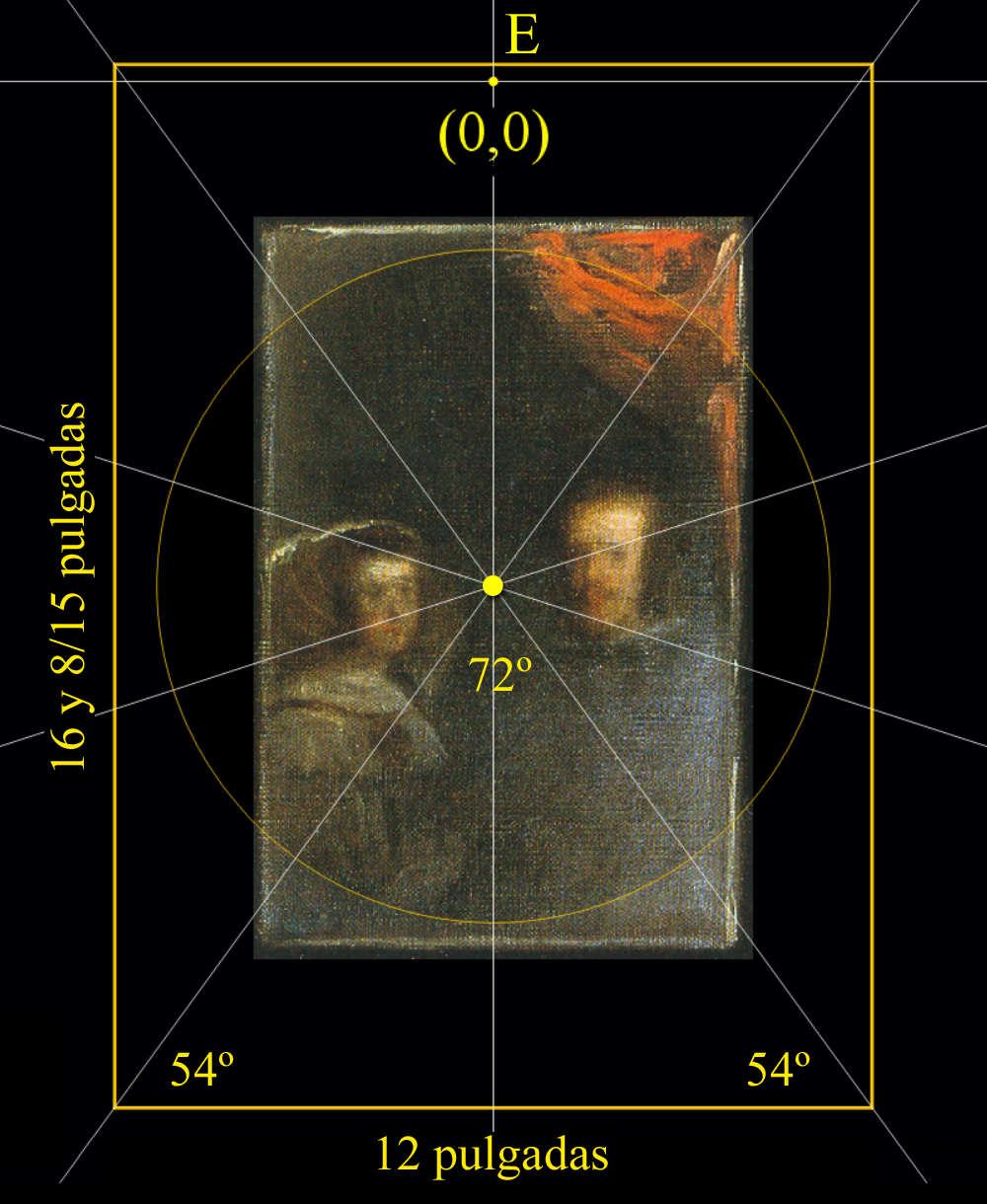
En estas imágenes se muestra, pues, el tamaño del área geométrica de una quinta parte de un pentágono regular, respecto al tamaño de 12 pulgadas de la anchura inscrita del marco del Espejo de Las Meninas.
En el siguiente paso verificaremos, pues, la altura del Marco del Espejo de Las Meninas, que mide 16,5333333.. pulgadas.
Para tal fin, calcularemos el tamaño correcto de la Apotema de este pentágono, que depende de la apertura del ángulo agudo de su centro, y, en ese caso, primero dividiremos los 360º de la circunferencia entre 10, que es igual a 36º, y, con la ayuda de la fórmula de la tangente de un ángulo, entonces, ya podremos deducir el tamaño de este cateto, es decir: la Apotema, x, del pentágono regular de 12 pulgadas de lado.
|
|
|
|
La fórmula de la tangente de un ángulo agudo, A, en un triángulo rectángulo es igual al cateto opuesto al ángulo analizado, y, dividido por el cateto contiguo, x, y, despejando, tenemos que el cateto contiguo, x, que trata del tamaño de la Apotema que buscamos, es igual al cateto adyacente, y, de 6 pulgadas, dividido por la tangente de 36º.
La tangente de 36º es aproximadamente igual a 0,726542...
y la altura del Marco del Espejo de Las Meninas corresponde, pues, a dos Apotemas, es decir; 8,258291... × 2 = 16,516583...pulgadas.
|
|
 |
|
|
Comprobemos, pues, el conocimiento trigonométrico del pintor español Diego Velázquez:
|
ALTURA DEL MARCO DEL ESPEJO |
≡ |
DOS APOTEMAS |
|
TOLERANCIA |
||||
|
16,533333... pulgadas |
- |
16,516583... pulgadas |
≡ |
0,016750... pulgadas |
≡ |
0,01884375 unidades |
≡ |
0,3894375 milímetros |
|
|
Como necesarios descubridores de esta pequeña tolerancia del 0,1%, equivalente a un residuo de 0,3894375 parte de un milímetro, reconocemos, una vez más, la confianza que transmite la perfecta Geometría que analizamos.
En definitiva, por las cuatro esquinas del marco del Espejo transitan, pues, la trayectoria a 54º de los dos vectores diagonales de su formato rectangular que determinaron el tamaño del ancho y alto del marco del Espejo, y, como brújula del gobierno, la presencia de los monarcas reflejados en la distancia legitiman el centro neurálgico del Imperio español.
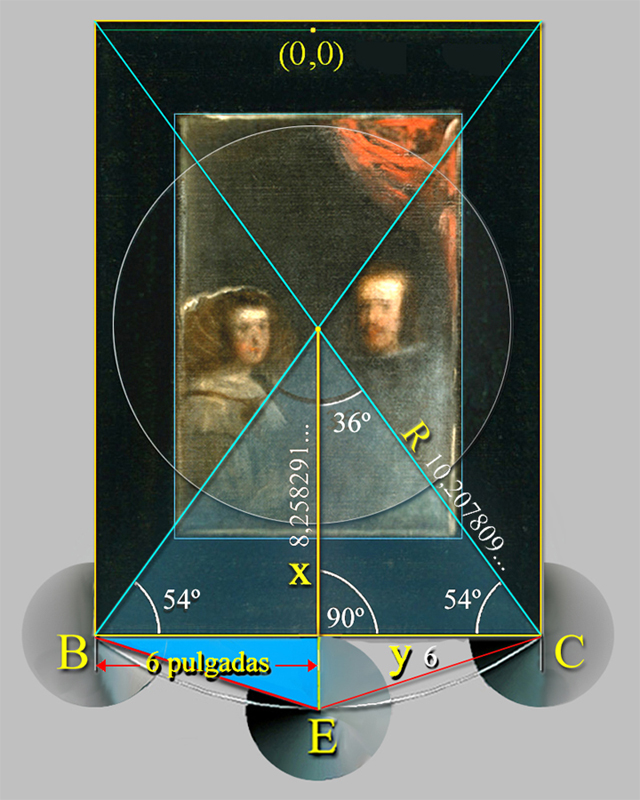
En la siguiente imagen se muestra la concepción del Espejo en el área geométrica de una quinta parte de un pentágono regular, cuyo lado BC de 12 pulgadas corresponde al tamaño de la anchura del marco del Espejo.
 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2R |
DIÁMETRO DEL PENTÁGONO |
= | 2 × 10,207809... pulgadas | ≈ | 20,415618... pulgadas | ≈ | 12 Φ + 1 |
2R ≈ 20,415618... pulgadas
12 Φ +1 ≈ 20,416407... pulgadas
|
TOLERANCIA |
0,000888638 unidades | ≈ | 0,0007899 pulgadas | ≈ | 0,018365175 milímetros |
EL ESPEJO & LA GEOMETRÍA SAGRADA
|
Diagonal del Espejo:
Diámetro del Espejo:
Diagonal Pitagórica:
La expresión 12 Φ + 1:
|
Estos cuatro resultados tienen una tolerancia común, imperceptible al ojo humano, de un tercio de milímetro.
| Elemento | Fórmula | p |
pulgadas | milímetros | |||
| Diagonal Pitagórica | √(16,533223...² + 12²) | ≈ | 20,429172... | 0 | 0 | ||
| Expresión Phi | 12 Φ + 1 | ≈ | 20,416407... | - 0,012765... | - 0,296786... | ||
| Diámetro del Espejo | 12 / seno(π/5) | ≈ | 20,415849... | - 0,013323... | - 0,309759... | ||
| Diagonal del Espejo | 2 × R | ≈ | 20,415618... | - 0,013554... | - 0,315130... | ||
| Diagonal Phi |
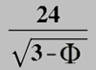 |
≈ | 20,415618... | - 0,013554... | - 0,315130... |
|
|
Estos resultados reflejan una exactitud extrema propia de la ingeniería o la óptica, que en la práctica de la pintura no se requiere, ya que hablamos de una pintura al óleo elaborada con un pincel.
El espejo de Las Meninas, donde Velázquez retrata a los monarcas, es, pues, la entrada a una de las diez esferas del Árbol Sagrado, la Sefira nº 9, Yesod, El Fundamento, que se la identifica con la Luna entre otros atributos, y, según la Kabala, su función particular es la de purificar y corregir a las demás Sefirot.
Dejemos, pues, que un especialista en la materia, Z´ev Ben Shimon Halevi, nos explique que representa Yesod en el Árbol Sagrado [10]:
|
En primer lugar, es generativo; desde este punto, como veremos, se manifiestan otros Árboles. En segundo lugar es reflexivo; aquí, directamente bajo Tiferet, se puede percibir una imagen de la imagen, y el Árbol se ve a sí mismo; Yesod es el espejo dentro del Espejo.
Estas dos funciones complementarias significan que su constitución, o Fundamento, debe ser clara y sólida; de ahí el significado interno de pureza sexual asociado a esta Sefirah. |
Pocas lecturas aclaratorias sobre Kabala se ha mostrado tan abiertamente atemporal, si se añadiera a esta definición una palabra de más quizá estaríamos hablando de otra cosa, pero no, hablamos de lo mismo.
Y se entiende, pues, que el propósito cabalístico de los reyes en el espejo está concebido de lo más comedido posible, porque, a través del significado sexual de esta Sefira, se explica la incertidumbre de la herencia de los Austrias.
De este modo Velázquez disponía en el Espejo a la Sefira nº 9, Yesod, el Fundamento, donde el rey Felipe IV y la reina Mariana de Austria refrendan, desde entonces, una Alianza divina.
Y ahora verificaremos si es verdad que la altura del Marco del Espejo de Las Meninas, que mide 16,5333333.. pulgadas, su tamaño exacto se ajusta con lo que afirmó Luca Pacioli en su libro DE DIVINA PROPORCIONE:
|
De ahí que entre los sabios se acostumbra a decir, según proverbio común: Aurum probatur ignis et ingenium mathematicis, es decir, que la bondad del oro la demuestra el fuego y la calidad de los ingenios las disciplinas matemáticas.
Y esta sentencia pretendía expresar que el genio apto para las matemáticas lo es también para las otras ciencias (...) |
La anchura del Marco del Espejo mide 13,5 unidades
Factorización de 3 x 3 x 3 x 5 = 135.
Los divisores del número 135 son 8:
1, 3, 5, 9, 15, 27, 45, 135.
135 ÷ 1,125 = 120; que es lo que mide en pulgadas el ancho original del lienzo de Las Meninas.
La altura del Marco del Espejo mide 18,6 unidades
Factorización de 2 x 3 x 31 = 186.
Los divisores del número 186 son 8:
1, 2, 3, 6, 31, 62, 93, 186.
186 ÷ 8 = 23,25; que es la cantidad que equivale en milímetros una pulgada castellana.
| LA ALTURA | FUNDAMENTO | LA ANCHURA | ||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula |
|
Unidades |
Pulgadas |
Metros |
|
| 0,3844 | 16 y 8/15 | 18,6 | = | 18,6 x 1 |
13,5 x 1 |
= |
13,5 |
12 |
0,279 |
|
| 0,3844 | 16 y 8/15 | 18,6 | = | 9,3 x 2 |
4,5 x 3 |
= |
13,5 |
12 |
0,279 |
|
| 0,3844 | 16 y 8/15 | 18,6 | = | 6,2 x 3 |
2,7 x 5 |
= |
13,5 |
12 |
0,279 |
|
| 0,3844 | 16 y 8/15 | 18,6 | = | 3,1 x 6 |
1,5 x 9 |
= |
13,5 |
12 |
0,279 |
|
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,6 x 31 |
0,9 x 15 |
= |
13,5 |
12 |
0,279 |
|
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,3 x 62 |
0,5 x 27 |
= |
13,5 |
12 |
0,279 |
|
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,2 x 93 |
0,3 x 45 |
= |
13,5 |
12 |
0,279 |
|
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,1 x 186 |
0,1 x 135 |
= |
13,5 |
12 |
0,279 |
|
|
|
| Marco del Espejo | Metros | Pulgadas | Unidades | Unidades por pulgada | Pulgadas reales | ||
| Anchura | 0,279 | 12 | 13,5 | = | 0,3 | x | 45 |
| Altura | 0,3844 | 16 y 8/15 | 18,6 | = | 0,3 | x | 62 |
|
|
La Cuadrícula de Aquiles
1125
unidades, que le corresponde el valor de 1000 pulgadas, es
un número de Aquiles:
72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, 1125...
Un número natural se llama poderoso cuando todos los exponentes de sus factores primos son mayores o iguales a 2.
Expresado de otra manera:
1125 se descompone en estos dos factores: 32 x 53.
Si N es poderoso, y un número primo, p, divide a N, entonces p2 también divide a N.
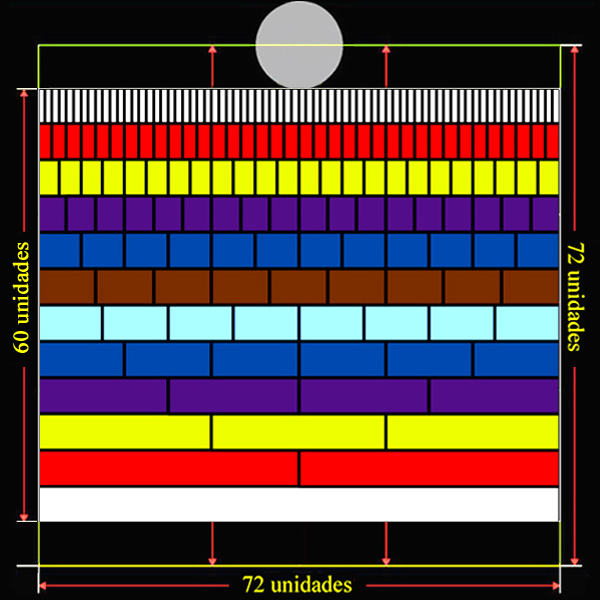
E, igualmente, 72 también es un número de Aquiles; que en la Geometría del ancho de la pared del fondo de Las Meninas quedó representado en doce distintas subdivisiones en la Tabla que denominamos La Cuadrícula de Aquiles.
| LA ALTURA |
LA ANCHURA |
|||||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||||
| 1,24 | 53,333 | 60 | = | 72 x 0,833 | 72 x 1 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 36 x 1,666 | 36 x 2 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 24 x 2,5 | 24 x 3 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 18 x 3,333 | 18 x 4 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 12 x 5 | 12 x 6 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 9 x 6,666 | 9 x 8 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 8 x 7,5 | 8 x 9 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 6 x 10 | 6 x 12 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 4 x 15 | 4 x 18 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 3 x 20 | 3 x 24 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 2 x 30 | 2 x 36 | = | 72 | 64 | 1.488 | |||
| 1,24 | 53,333 | 60 | = | 1 x 60 | 1 x 72 | = | 72 | 64 | 1.488 | |||
|
|
La Cuadrícula de Aquiles, que cubre totalmente a la anchura de la pared del fondo, es la base geométrica del bastimento de Las Meninas.
Ante este Muro se estableció una relación de dependencia, donde el más fuerte, el rey Felipe IV, daba protección y ennoblecía al más débil, Diego Velázquez, a cambio de comprometerse a guardar fidelidad y ejecutar, de manera segura, un trabajo cabalístico.
Ratio de la pared del fondo
60 unidades ÷ 72 unidades = 5 ÷ 6 = 0,83333...
Y se demuestra, pues, que el maestro español utilizó en este óleo una exacta Geometría, Aritmética y Matemática; considerando en esta investigación, además, otras ciencias alternativas, pero vedadas en esta época.
Aportamos, pues, cuatro aspectos o equivalencias de cualquier medida en la aplicación de la pulgada castellana en el estudio de este lienzo.
|
Cuadrícula geométrica |
Unidades de trabajo |
Medidas castellanas |
Sistema métrico |
|
1 cuadradito |
3 |
pulgadas |
milímetros |
|
2,666666 |
62 |
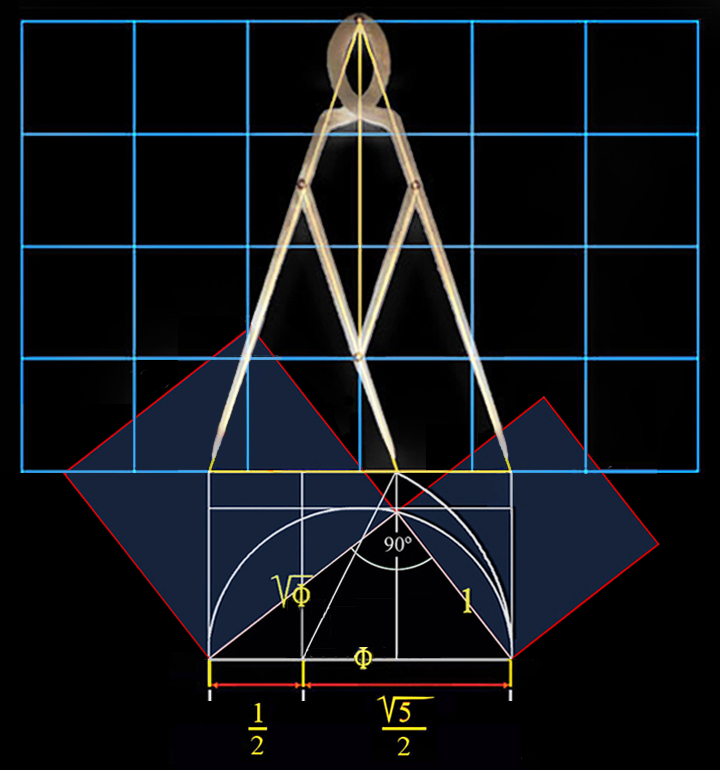
El Compás
El compás es un instrumento que sirve para trazar la figura
más perfecta de todas; el círculo, cuyo diseño triangular está asociado desde la
antigüedad a la forma de la letra griega
alfa mayúscula A.
|
|
La voz de la Sabiduría
Cuando componía los cielos, allí estaba yo, señalando por compás la sobrefaz del abismo.
בהכינו שׁמים שׁם אני בחוקו חוג על־פני תהום׃
Proverbios 8:27 |
Luca Pacioli - Divina Proporción Edición 1509 |
El compás representa, por tanto, varias cuestiones emblemáticas universales:
La herramienta del acto de la Creación divina - Dios Arquitecto,
el útil de acotación del límite del espacio,
el símbolo de la Matemática, Geometría y Arquitectura
y, también, a la tercera de las tres Grandes Luces que ilumina toda logia masónica.
 |
|
|
El compás de proporción, construido por Marco Antonio Mazzoleni en 1606 siguiendo las instrucciones de Galileo Galilei, permitía, sin conocimientos matemáticos, dividir una línea en las partes que se desease, reproducir un plano a diferentes escalas o extraer raíces cuadradas y cúbicas [11].
El precursor del compás de Galileo fue el compás de proporción de ocho puntas del matemático italiano Fabrizio Mordente, que, con dos brazos con punteros, permitía la solución de problemas en la medición de la circunferencia, área y ángulos de un círculo.
En 1567 Fabrizio Mordente publicó en Venecia, en una simple hoja impresa, el tratado e ilustraciones de su dispositivo [12].
|
Compás de proporción |
Compás de reducción adaptado a Las Meninas |
||
|
Compás de reducción de eje desplazable |
Toda una joya en la época de Velázquez [13].
El compás de eje desplazable consiste en dos piezas calibradas, fijadas a un centro móvil, donde la medición se traduce a escalas entre 1:2 a 1:15.
Este compás de cuatro puntas se utiliza para reproducir dibujos a mayor o menor tamaño; en la práctica de la pintura facilita medir objetos reales o bocetos preparatorios para ser plasmados a su formato definitivo en la superficie del lienzo.
LA GEOMETRÍA DE LA PROPORCIÓN
|
PLANTEAMIENTO
EL PROCEDIMIENTO
LA ESCALA
LA PROPORCIÓN
|
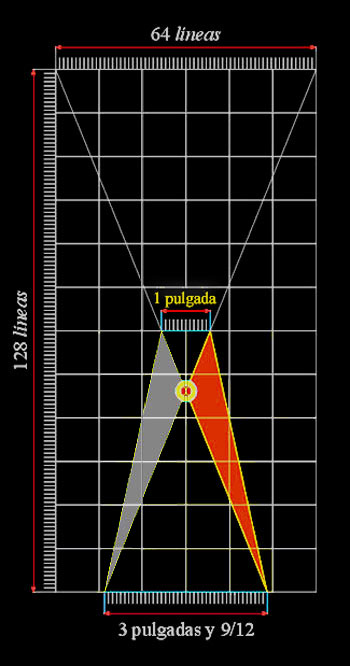 Apertura adaptada a Las Meninas |
Escribe Vitrubio en el capítulo II del Libro Noveno de Los Diez Libros de Arquitectura [14]:
Pitágoras inventó una escuadra que no requiere el trabajo de los artesanos, (...).
|
La escuadra perfecta |
|
Si se toman tres reglas, una de tres pies, otra de cuatro y una tercera de cinco, y se las junta de modo que reunidos sus extremos de punta a punta formen un triángulo, se tendrá una escuadra perfecta. |
Hablamos, pues, del Triángulo Sagrado egipcio, nombre moderno dado a un triángulo rectángulo cuyo lados miden; 3, 4 y 5, o sus medidas preserven estas proporciones, como es el caso del triángulo rectángulo semejante de lados; 15, 20 y 25 codos, que se empleó en el Antiguo Egipto, y fue llamado Isíaco en honor a la diosa Isis.
 |
|
|
Estos tres números, 3, 4 y 5, utilizados para obtener un ángulo recto, tienen propiedades aritméticas y geométricas especiales, además de coincidencias con períodos astronómicos, tales como el período de revolución sinódica de un planeta visible a simple vista, o los múltiplos mínimos comunes de varios de esos períodos.
Será, por tanto, estos tres números pitagóricos los que midan el espacio profundo de Las Meninas.
LA PROPORCIÓN
Aplicaremos, pues, el Teorema de Pitágoras [15], más el cálculo de las medidas de los lados de los triángulos semejantes de Euclides [16], para averiguar la razón geométrica entre el tamaño real de la Habitación del Príncipe y el de la distante pared representada en Las Meninas.
Comprobaremos en un ejemplo práctico la relación matemática entre pulgadas y unidades en consonancia con las profundidad de este lienzo.
Para esta demostración daremos el valor de 60 pulgadas al tamaño de la anchura real de la Habitación del Príncipe, y 18 unidades a la anchura de la pared del fondo pintada en este óleo.
|
La razón geométrica es la comparación de dos cantidades por su cociente, donde se evalúa cuántas veces contiene una a la otra. |
Con estas medidas reseñadas obtendríamos la siguiente propuesta en un compás abierto de cuatro puntas:
|
|
|
|||||||||||
|
|
|
Hablamos, pues, de la misma Geometría de los egipcios, la de Pitágoras, la de Thales de Mileto, la de Euclides ... y la de Diego Velázquez.
Como se demuestra, la razón geométrica 60 / 18 = 3,333333... pulgadas por unidad operaría del siguiente modo en Las Meninas:
x = 18 representaría el tamaño proporcional en unidades del ancho de la pared pintada del fondo.
y = 60 representaría el tamaño proporcional en pulgadas del ancho real de la Habitación del Príncipe.
Y obtendríamos el mismo ratio, entre la anchura y altura real de esta sala respecto a los del tamaño de la pared del fondo pintada en este óleo, con los siguientes guarismos:
240 / 72 = 200 / 60 = 3,333333... pulgadas por unidad
|
|
|
|||||||||||||||||||||
|
|
Sea 240 pulgadas el tamaño real de la anchura de la Habitación del Príncipe,
y 72 unidades el valor de la anchura de la pared del fondo pintada en este óleo:
240 pulgadas / 72 unidades = 3,333333... pulgadas por unidad.
El uso práctico del triángulo pitagórico; 3, 4 y 5 en el cono visual de Las Meninas es una prueba contundente del dominio de la Geometría Sagrada, además de la aplicación por Diego Velázquez de los principios pitagóricos en la perspectiva de esta pintura.
El indicio de la existencia de una constante matemática da pie para garantizar, ahora sí, el estudio de la perspectiva de la Habitación del Príncipe.
|
|
El formato geométrico de la pared del fondo de Las Meninas trata, pues, de una proporción sesquiquinta, que es aquella que contiene la unidad y un quinto de ella:
|
5/5 + 1/5 = 6/5
1 + 1/5 = 1,2 |
Y así mismo, la relación matemática entre la altura y la anchura 5/6 = 0,833333... en la música pitagórica representa el tono menor o la proporción entre las notas Re y Fa, o Sol y Si bemol, una consonancia de tercera menor, esencial para la armonía.
En resumen, el tamaño de la pared del fondo de 72 x 60 unidades no es accidental, ya que está diseñada para encarnar la Tercera Menor, es decir; la proporción 5/6 y 6/5, una de las consonancias fundamentales que, junto con la Cuarta Justa; 4/3 y la Quinta Justa; 2/3, forma la base de la Música occidental.
Segundo Caso
Se entiende, pues, que trabajando sólo en pulgadas, la escala de representación de la pared del fondo de Las Meninas sería:
60 / 16 = 3,75, y el inverso; 1/3,75 = 0,266666...
x = 16 representaría el tamaño proporcional en pulgadas del ancho de la pared pintada del fondo.
y = 60 representaría el tamaño proporcional en pulgadas del ancho real de la Habitación del Príncipe.
|
|
|
|||||||||||
|
|
|
La escala de representación de la pared del fondo de Las Meninas es de: 1/3,75 = 0,266666...
Este análisis demuestra, pues, que las dos constantes de escala para la perspectiva están basadas en fracciones puras:
|
CONSTANTE |
RATIO |
VALOR DECIMAL |
CONVERSIÓN |
|
Escala 1 |
Profundidad Armónica: 10/3 |
3,333333... |
Pulgadas reales por unidades |
|
Escala 2 |
Proporción Métrica: 15/4 |
3,75 |
Pulgadas reales por pulgadas en la distancia |
CONCLUSIÓN:
Y se deduce, pues, que si hemos dado respuesta segura al método pitagórico que utiliza Velázquez para medir distancias, a su vez, también hemos definido el propósito del espacio vacío de la mitad superior de la Habitación del Príncipe, donde, además de contener aire, el pintor español refrendó, en la primera esfera denominada Kether, el símbolo soberano de la autoridad monárquica teocrática:
LA CORONA
|
|
|
|
De acuerdo con el resultado del análisis mostrado, todo apunta a que han sido restituido los números originales que acompañan la altura y profundidad de esta pieza artística, por lo que ahora sería consecuente, pues, dotar a estos guarismos de la hondura simbólica que promueven.
 |
 |
 |
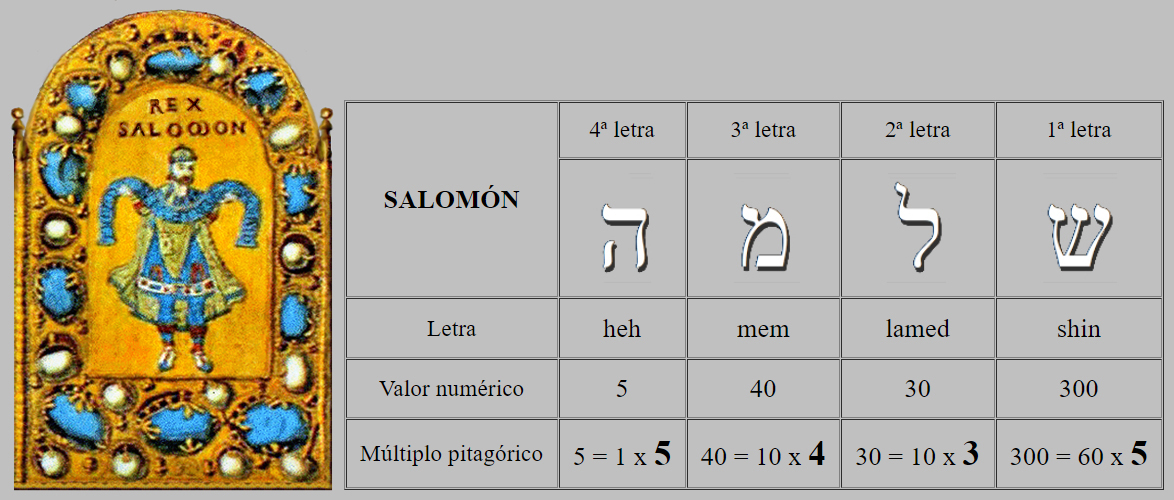
 |
|||||
| 5 | + | 40 | + | 30 | + | 300 | = | 375 |
|
|
Gematría del nombre Salomón
Factorización de 3 x 5 x 5 x 5 = 375.
Los divisores del número 375 son 8: 1, 3, 5, 15, 25, 75, 125, 375.
 |
|
Los números asociados con Marte son: 5, 15, 25, 75, 125, 375.
Cada fila, columna y diagonal suma 65, y todos los números de este cuadrado suman un total de 325 |
Geburah, la Sefira nº 5, puede manifestarse como la aplicación de la ley, el rigor, la necesidad de establecer límites claros y la capacidad de confrontar la negatividad, se traduce, generalmente, como Severidad, Justicia, Poder o Fuerza, y representa, pues, la cualidad divina de la justicia, la disciplina, la restricción y el juicio.
Es la fuerza que impone límites y aplica el orden, tal es el significado que se extrae, pues, del nombre de Salomón, שלמה.
Pero, hay algo más acerca del número 375, que ya habíamos hablado de él como el valor del denominador del Pi del mismísimo Diego Velázquez, y que es el resultado de la Gematría del nombre de SALOMÓN.
|
CONSTANTE DE PI |
VALOR NUMÉRICO |
FRACCIÓN | DESVIACIÓN |
ORIGEN HISTÓRICO |
|
Velázquez |
3,141333333... |
1178/375 | 0,000259321... |
Codificado en Las Meninas |
|
1178/375 = 3,141333... |
 |
|
|
El Libro de Proverbios se divide, pues, en varias colecciones, y sólo una de ellas es la que se atribuye a Salomón, que contiene exactamente 375 aforismos breves, en la sección Proverbios 10:1 - 22:16.
|
La esperanza que se prolonga, es tormento del corazón; mas el Árbol de Vida es el deseo cumplido.
תוחלת ממשׁכה מחלה־לב ועץ חיים תאוה באה׃ Proverbios 13:12
El fruto del justo es Árbol de Vida; y el que gana almas, es sabio.
פרי־צדיק עץ חיים ולקח נפשׂות חכם׃
Proverbios 11:30 |
La distancia entre la vista y lo que se ve ha de ser
proporcionada; ya que el tamaño de cualquier objeto o figura, aunque se localice
muy distante, debe armonizar con la lejanía plasmada en el lienzo.
Y como indicó Francisco Pacheco, el maestro de Velázquez:
Así la distancia ha de corresponder a la vista con cierta razón y proporción de ángulos.
 |
|
|
El ancho del lienzo de Las Meninas mide la mitad de la anchura de la Habitación del Príncipe, y el tamaño de la anchura de la pared pintada equivale a 1/3,75 de esta misma sala [17].
La anchura inicial de Las Meninas es de 120 pulgadas, que corresponde a 2,79 metros.
Luego la anchura de esta sala será de 2,79 metros x 2 = 5,58 metros = 20 pies = 240 pulgadas.
La dimensión transversal de la distante pared pintada es de 1,488 metros = 64 pulgadas.
La relación entre el tamaño de como se pinta la pared del fondo y su tamaño real: 1,488/5,58 = 0,266666...
Luego la escala de representación de la pared del fondo es de: 1/3,75 = 0,266666..
|
Zona izquierda 132 pulgadas |
Zona central 64 pulgadas |
Zona derecha 44 pulgadas |
||
|
44 |
44 |
44 |
64 |
44 |
|
Total - 240 pulgadas |
||||
Desglose de la anchura de la Habitación del Príncipe
La cuestión del tamaño de la pared del fondo está
relacionada directamente con
la perspectiva:
|
|
|
|
|
|
|
|
|
|
|
unidades |
pulgadas |
medidas castellanas |
metros |
|
Altura |
225 |
200 |
200 / 12 = 16 pies y 2/3 |
4,65 |
|
Anchura |
270 |
240 |
240 / 12 = 20 pies |
5,58 |
|
|
Más allá de lo ya analizado, pondremos a prueba un Caso especial de medición en la distancia, y su relación matemática con la rejilla de trabajo.
Ya hemos observado que el ancho del lienzo de Las Meninas equivale a la mitad de la anchura de la Habitación del Príncipe, y que la anchura real de esta misma sala está representada, proporcionalmente, en la pared del fondo de esta pintura.
Esta relación se descubre del siguiente modo; 120 pulgadas corresponden, pues, al tamaño original de la anchura de Las Meninas, y 64 pulgadas es lo que mide la anchura de la pared del fondo pintada en este lienzo:
64/120 = 8/15 = 0,533333...
|
Unidades en la pared del fondo |
La pulgada en 15 partes |
Milímetros |
Ratio de ampliación |
|
1,125 |
15/15 |
23,25 |
3,333333... x 1,125 = 3,75 |
|
0,6 |
8/15 |
12,4 |
3,333333... x 0,6 = 2 |
|
0,3 |
4/15 |
6,2 |
3,333333... x 0,3 = 1 |
|
|
Y al mismo tiempo, el coeficiente de ampliación de 3,75 confirma que el Tamaño real de esta sala de 240 pulgadas de anchura está en relación directa con la distancia sugerida en la pared pintada del fondo de Las Meninas:
64 pulgadas x 3,75 = 240 pulgadas
En cualquier caso, desde la antigüedad la relación entre el tamaño aparente y la distancia percibida de un objeto determinado del campo visual quedó formulada en la denominada Ley de Euclides, que dice así:
|
La distancia entre el objeto y el observador es inversamente proporcional al tamaño de dicho objeto. |
El tamaño de un objeto disminuye en función a la distancia de forma inversamente proporcional, es decir; a doble de distancia a este mismo objeto le corresponde la mitad de su tamaño.
Acerca de la distancia entre el primer plano de Las Meninas y la pared del fondo habría que puntualizar que existe la posibilidad de entender esta distancia de dos manera diferentes;
una sería la profundidad real de la Habitación del Príncipe,
y la otra, la que pinta Velázquez en su óleo en base a las proporciones que estamos ahora analizando.
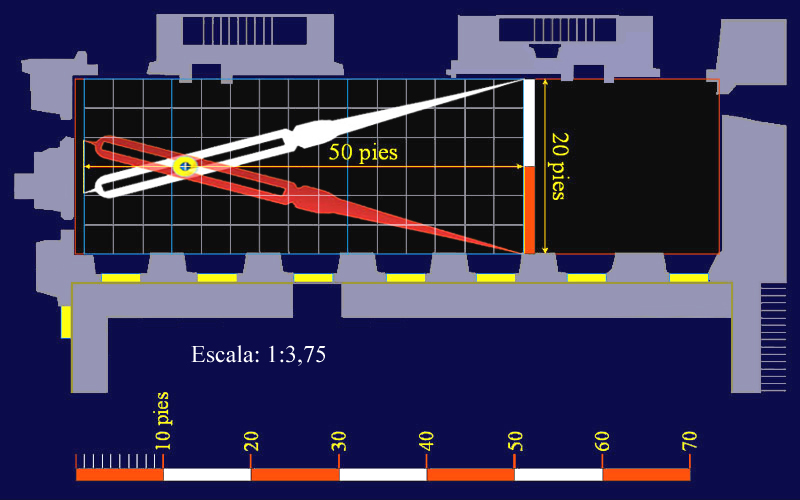
Examinaremos, pues, la profundidad real de esta sala situada en la esquina suroeste de la planta baja del Alcázar de Madrid.
 |
|
|
El arquitecto del rey Juan Gómez de Mora armonizó las primitivas construcciones que integraban el Alcázar madrileño mediante una larga fachada flanqueada por torreones, es decir; él fue quien hizo el plano de Palacio que aquí estudiamos.
LA POSICIÓN DEL PINTOR ANTE LA PROFUNDIDAD
La posición del pintor ante la profundidad de esta sala mide 50 pies,
50 pies equivalen; 50 x 12 = 600 pulgadas,
y 600 pulgadas equivalen; 600 x 0,02325 metros por pulgada = a 13,95 metros.
|
|
|
|
Y
cierto es que 0,279 metros equivalen al Pie Real, y que la anchura de
Las Meninas medía 2,79 metros, una anchura que corresponde a diez veces
el Pie Real; es decir, a 120 pulgadas.
Una reciprocidad consistente en la que sólo intervienen números enteros.
En pintura, la mirada del pintor se propaga en las distancias, estudia las diferentes calidades de luz, en las penumbras y sombras, en las luces claras y oscuras, en las frías y calientes; de tal manera, que la superficie del lienzo funciona como un plano transparente, vertical al suelo, en la intersección con su modelo.
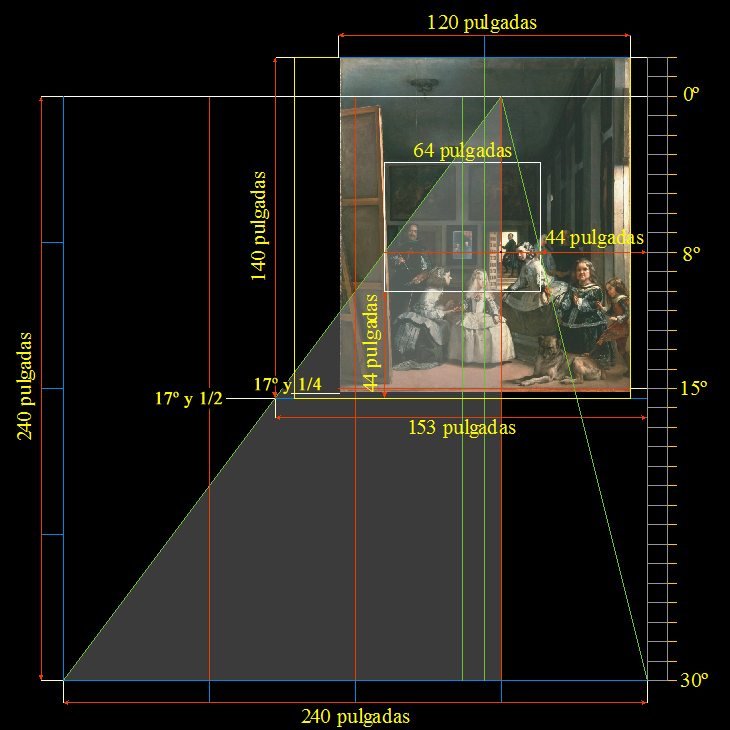 |
Calibración de la anchura y altura del lienzo de Las Meninas
Escala 1:2 |
|
|
Al
rey de Egipto Meris se le atribuye la invención de la Geometría, y desde
entonces vino la facultad del medir, que, poco a poco, creció en nuevas
invenciones hasta los tiempos de Pitágoras, natural de la isla de Samos.
Cuentan que Pitágoras ideó las delineaciones, las formas, los intervalos, las distancias y las cantidades; entre las cuales halló la virtud de la potencia del triángulo rectángulo, con tanto contentamiento y satisfacción de haberle hallado, que se dice que en pago de la merced recibida ofreció a la diosa Minerva el sacrificio Hecatombe en el cual sacrificó cien vacas.
|
|
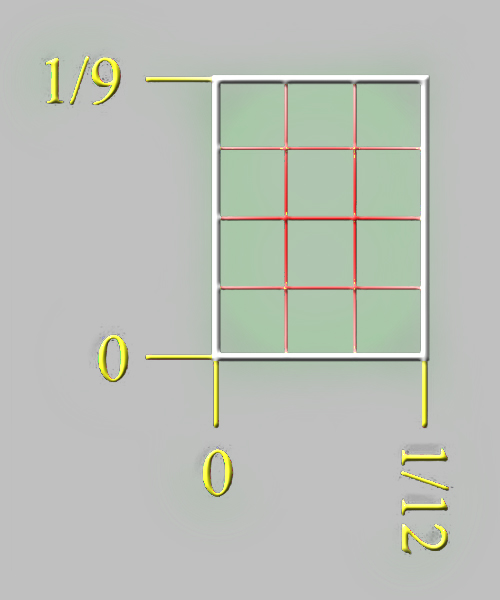 |
No obstante, valoramos, pues, la erudición de Velázquez al hacer gala en Las Meninas de su grado de Maestro de Matemática, Magister Matheseos, una prueba académica que consistía, desde la Edad Media, en una demostración original del Teorema de Pitágoras, lo que acreditaba una sólida formación de Matemática y Geometría.

Ha tomado 350 años descubrir un plano concluyente que mostrara gráficamente la gestación del trabajo geométrico de Las Meninas, y posibilitara reconstruir, con total exactitud, la localización de cada elemento necesario y principal de esta composición.
El conocimiento del sistema de medidas de la época de Velázquez facilita acceder a las habituales normas ópticas y geométricas de la profundidad espacial, pero también proporciona, a ciencia cierta, el modelo e idea original del trazado de la Geometría de esta pintura, lo cual constituye, además, la recuperación del plano inicial de Las Meninas.
Esta comprometida empresa está basada en dos ideas complementarias que garantizan la legítima génesis geométrica de Las Meninas:
Una la del Teorema de Tales de Mileto [18], que afirma que cualquier ángulo inscrito en un semicírculo es un ángulo recto,
y la otra compartida por dos ilustres geómetras; el Teorema de Pitágoras y la Proposición 47 de Euclides [19].
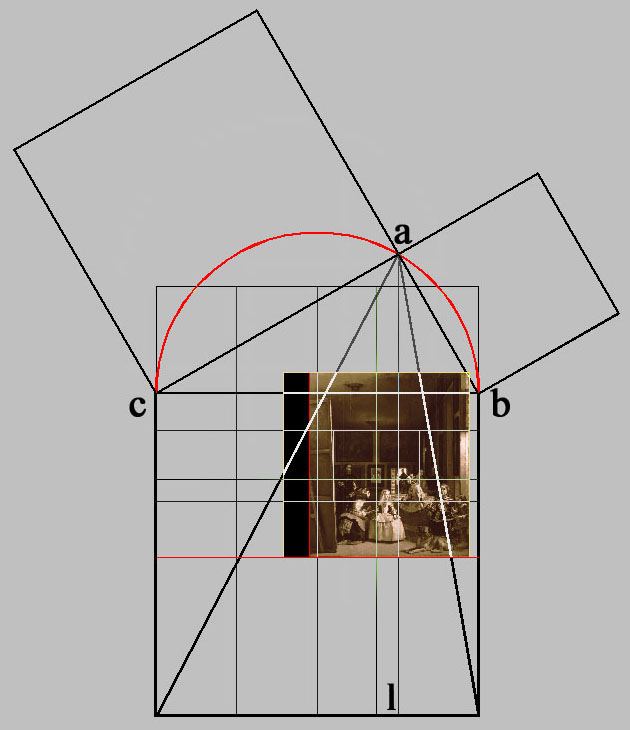
Tamaño del área geométrica de Las Meninas en pulgadas castellanas.
 |
|
al describe el eje vertical del punto de fuga:
cb + ad = al = 2 + √3/2 |
La Habitación del Príncipe mide 240 pulgadas de ancho, y el eje vertical
al mide físicamente; 240 pulgadas + 60√3 pulgadas.
60√3 equivale geométricamente a; ab2 - bd2 = ad2.
Ahora sustituiremos estas letras por cifras; si ab = 120 y bd = 60; luego ad = √ (1202 - 602) = √10800 = 60√3.
Como hemos confirmado, el ancho del área geométrica de Las Meninas equivale a 240 pulgadas.
|
Formato |
Proporción |
Pulgadas por unidad |
|
La anchura |
Tamaño en metros |
||
|
8 |
8/9 |
0,888.888 |
× |
72 unidades |
= |
64 pulgadas |
8 × 8 × 0,02325 = 1,488 metros |
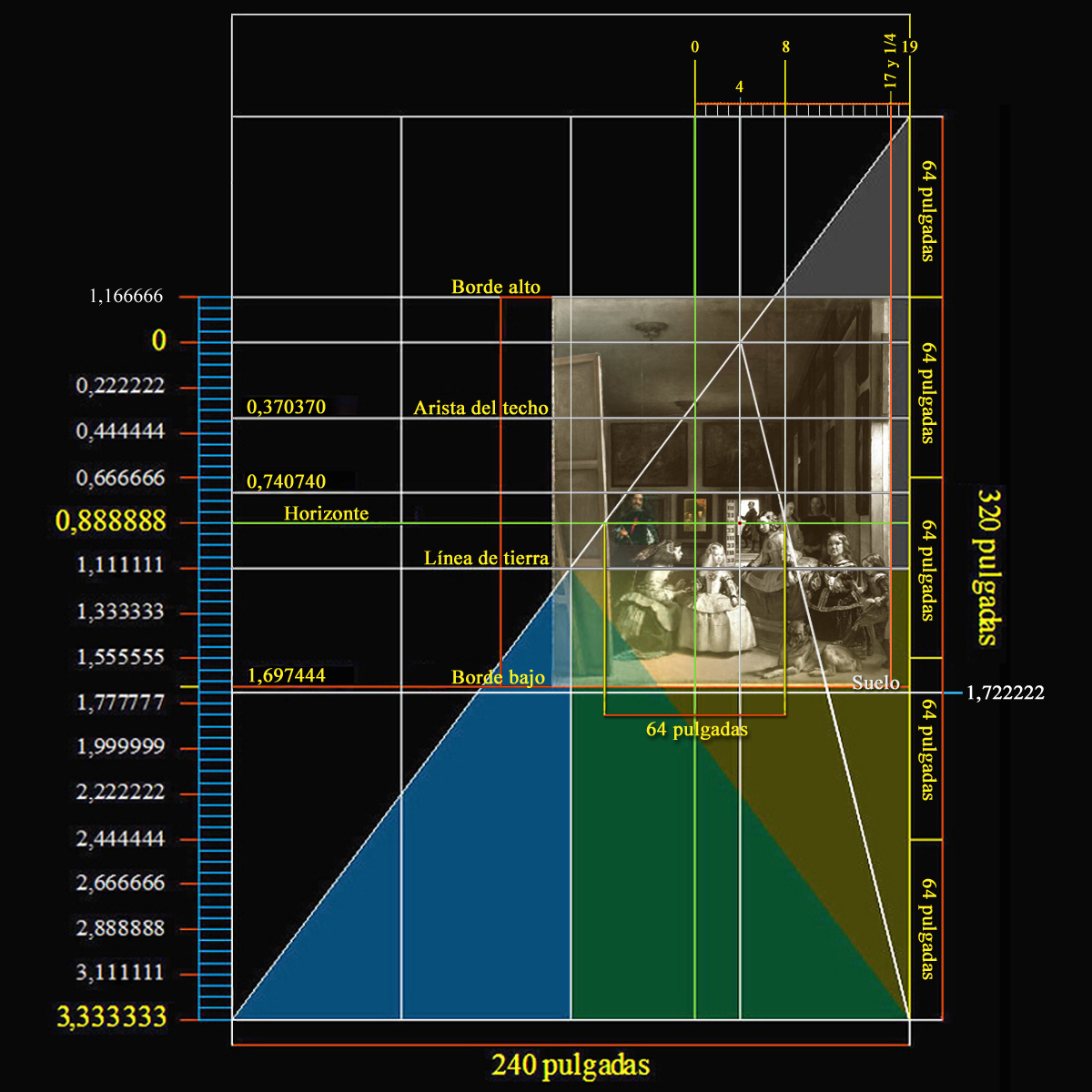
ANCHURA PARED DEL FONDO
|
DEMOSTRACIÓN
Luego la escala de representación de la pared del fondo será:
64 / 240 = 0,888888... / 3,333333... = 0,266666... = 1 / 3,75. |
 |
|
|
| Lado del Triángulo | Cateto menor | Cateto mayor | Hipotenusa |
| Medidas en pulgadas | 80 x 3 = 240 | 80 x 4 = 320 | 80 x 5 = 400 |
| Divisiones | 60 x 4 partes | 64 x 5 partes | 100 x 4 partes |
|
|
Este plano mide físicamente 240 x 352 pulgadas, es decir; 5,58 x 8,184 metros.
Luca Pacioli manifiesta
en su tratado DE DIVINA PROPORTIONE que el saber tuvo su origen en el sentido de
la vista; y de ahí que la vista es la primera puerta por la que el intelecto
entiende y gusta.
En el Renacimiento, y de acorde con la idea de que el hombre es la medida de todas las cosas, se aplicó la proporcionalidad del cuerpo humano a todo tipo de arte:
Un sistema antropométrico de medición consolidado en dedos, codos, palmos o pies.
 |
|
|
En la Villa Barbaro, proyectada por Palladio, encontramos un ejemplo bien ilustrado de un cazador asomado a una puerta simulada, y autorretrato del pintor Paolo Veronés, fundido en el conjunto de la obra arquitectónica, a semejanza de la idea de Leonardo da Vinci, como también lo fue para Alberto Durero, en la que toda práctica pictórica debía sustentarse en la ciencia de la Matemática y Geometría.
En nuestro ejemplo, José Nieto, el Aposentador de la reina, será quien salvaguarde la proporción y el tamaño real de cada objeto en la distancia.
La anchura de la Puerta mide 18,9 unidades
Factorización de 3 x 3 x 3 x 7 = 189.
Los divisores del número 189 son 8:
1, 3, 7, 9, 21, 27, 63, 189.
La altura de la Puerta mide 30 unidades
Factorización de 2 x 3 x 5 = 30.
Los divisores del número 30 son 8:
1, 2, 3, 5, 6, 10, 15, 30.
| LA ALTURA | LA ANCHURA | |||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 0,62 | 26 y 10/15 | 30 | = | 30 x 1 | 18,9 x 1 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 15 x 2 | 6,3 x 3 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 10 x 3 | 2,7 x 7 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 6 x 5 | 2,1 x 9 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 5 x 6 | 0,9 x 21 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 3 x 10 | 0,7 x 27 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 2 x 15 | 0,3 x 63 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 1 x 30 | 0,1 x 189 | = | 18,9 | 16 y 12/15 | 0.3906 | |
|
|
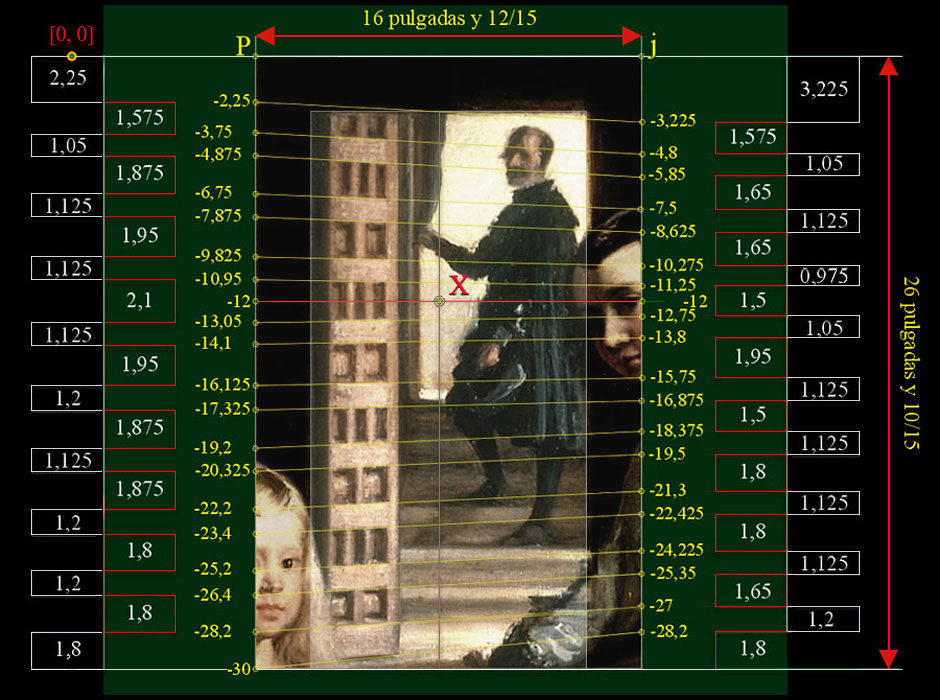
Señalaremos la idea más compleja; la puramente geométrica de esta Puerta de madera.
 |
|
División de la altura de 30 unidades equivalente a 26 pulgadas y 10/15 |
La división de la altura de 30 unidades de la puerta en la rejilla de trabajo:
30 unidades / 0,075 unidades = 400 partes.
| Unidades | Fracción de la pulgada | Pulgadas | Milímetros | Operación | Tamaño real | |
| 1,125 | 15/15 | 1 | 23,25 | 1,125 unidades x 3,333333... pulgadas por unidad | = | 3,75 pulgadas |
| 0,075 | 1/15 | 0,066666... | 1,55 | 0,075 unidades x 3,333333... pulgadas por unidad | = | 0,25 de pulgada |
|
|
Matemáticamente, pues, hemos acotado diecinueve alturas niveladas por el Horizonte de Las Meninas, y así rehacer el trazado de la Puerta de madera semiabierta de 22 cuarterones en el vano de la anchura de las dos jambas.
La escala, ya sea de ampliación o disminución, es la relación entre el tamaño real de un objeto y su tamaño final en el dibujo.
Así, en este caso, una escala de 1/3,75 significa que en la distancia una pulgada en la pared del fondo de Las Meninas, y cuyo valor en la rejilla de trabajo es de 1,125 unidades, representa en el mundo real a 3,75 pulgadas.
Escala de la pared del fondo: 1/3,75
| Unidades | Fracción de la pulgada | Pulgadas | Pulgadas reales en la distancia |
| 2,1 | 1 pulgada y 13/15 | 1,866666 | 7 pulgadas = 7 |
| 2,025 | 1 pulgada y 12/15 | 1,8 | 6 pulgadas 9/12 = 6,75 |
| 1,95 | 1 pulgada y 11/15 | 1,733333 | 6 pulgadas 6/12 = 6,5 |
| 1,875 | 1 pulgada y 10/15 | 1,666666 | 6 pulgadas 3/12 = 6,25 |
| 1,8 | 1 pulgada y 9/15 | 1,6 | 6 pulgadas = 6 |
| 1,725 | 1 pulgada y 8/15 | 1,533333 | 5 pulgadas 9/12 = 5,75 |
| 1,65 | 1 pulgada y 7/15 | 1,466666 | 5 pulgadas 6/12 = 5,5 |
| 1,575 | 1 pulgada y 6/15 | 1,4 | 5 pulgadas 3/12 = 5,25 |
| 1,5 | 1 pulgada y 5/15 | 1,333333 | 5 pulgadas = 5 |
| 1,425 | 1 pulgada y 4/15 | 1,266666 | 4 pulgadas 9/12 = 4,75 |
| 1,35 | 1 pulgada y 3/15 | 1,2 | 4 pulgadas 6/12 = 4,5 |
| 1,275 | 1 pulgada y 2/15 | 1,133333 | 4 pulgadas 3/12 = 4,25 |
| 1,2 | 1 pulgada y 1/15 | 1,066666 | 4 pulgadas = 4 |
| 1,125 | 1 pulgada = 15/15 | 1 | 3 pulgadas 9/12 = 3,75 |
| 1,05 | 14/15 de pulgada | 0,933333 | 3 pulgadas 6/12 = 3,5 |
| 0,975 | 13/15 de pulgada | 0,866666 | 3 pulgadas 3/12 = 3,25 |
| 0,9 | 12/15 de pulgada | 0,8 | 3 pulgadas = 3 |
|
|
La
Geometría euclidiana es una rama de la Matemática que se ocupa del estudio de las
propiedades de las figuras en el plano y en el espacio; incluyendo puntos,
rectas, superficies...
 |
|
|
La base teórica del dibujo técnico queda establecida, pues, por los instrumentos usados para su práctica; como la regla, el compás, la escuadra..., mientras que el razonamiento matemático se ocupa de las operaciones elementales, que originan series matemáticas.
Es cierto, pues, que tanto el dibujo técnico como el razonamiento matemático comparten una base común en la Geometría y la Lógica, aunque se diferencian en sus aplicaciones y enfoques para la representación espacial y el análisis de formas.
|
INTERVALO DEL MARCO DE LA PUERTA |
||
| 30 ÷ 81 | = |
1,111111111... - 0,740740740... = 0,370370370... |
|
|
||
|
TAMAÑO DE 1/6 DE INTERVALO |
||
| 5 ÷ 81 | = | 0,370370370... ÷ 6 = 0,061728395... |
 |
|
|
| 60 ÷ 81 | = |
ORIGEN DE COORDENADAS |
= | 0,740740740... |
| 65 ÷ 81 | = | 0,740740740... + 0,061728395... | = | 0,802469136... |
| 70 ÷ 81 | = | 0,802469136... + 0,061728395... | = | 0,864197531... |
|
72 ÷ 81 |
= |
HORIZONTE |
= | 0,888888888... |
| 75 ÷ 81 | = | 0,864197531... + 0,061728395... | = | 0,925925925... |
| 80 ÷ 81 | = | 0,925925925... + 0,061728395... | = | 0,987654321... |
| 85 ÷ 81 | = | 0,987654321... + 0,061728395... | = | 1,049382716... |
|
LÍNEA DE TIERRA |
||||
| 90 ÷ 81 | = | 1,049382716... + 0,061728395... | = | 1,111111111... |
|
|
Y la altura del marco de la Puerta del fondo de Las Meninas mide 30 unidades.
Tenemos:
30 unidades / 0,075 unidades = 400 partes.
La altura de la jamba queda dividida, por tanto, en cinco partes iguales:
400 partes / 5 = 80 partes.
Y al mismo tiempo:
0,075 unidades x 80 partes = 6 unidades por cada 1/5 de la altura de la Puerta del fondo.
 |
|
|
La perspectiva lineal, surgida de la observación, negaba los postulados geométricos aceptados en el siglo XV; sin embargo, en el año 1656, cuando se pintan a Las Meninas, ya existía suficiente Matemática y Geometría que engranase del todo los números analizados, y, no obstante, en la que toda práctica pictórica debe sustentarse.
|
Piero della Francesca es el único pintor del Renacimiento que hace uso de una Matemática sofisticada, la cual supuso el puente entre la perspectiva artística y la geométrica. |
A la muerte de Piero della Francesca sus investigaciones inspiró a notables autores de tratados de Geometría, como es el ejemplo del libro DE DIVINA PROPORTIONE de Luca Pacioli, ilustrado por Leonardo da Vinci, donde están presentes los estudios de Piero sobre los sólidos geométricos.
 |
|
 |
|
 |
| Fuego | Tierra | Universo | Aire | Agua |
| tetraedro | hexaedro | dodecaedro | octaedro | icosaedro |
|
|
En la Geometría de Euclides las paralelas son siempre equidistantes, y por mucho que se las prolonguen nunca se encuentran en un sólo punto; pero en la Geometría no euclidiana, generada de la experiencia del campo visual, este postulado se revelaba falso, pues, como demostró Filippo Brunelleschi, en el punto de fuga se concentran todas las paralelas a la altura del nivel de ojo u Horizonte.
|
|
|
|
Este análisis confirma que en Las Meninas la profundidad escalonada de los cinco planos laterales de la arquitectura de la pared derecha están dispuestos de manera segura.
|
Intervalo |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
Unidades |
2,75 |
|
3,5 |
|
5 |
|
8 |
|
14 |
|
Pulgadas |
2 pulgadas y 4/9 |
|
3 pulgadas y 1/9 |
|
4 pulgadas y 4/9 |
|
7 pulgadas y 1/9 |
|
12 pulgadas y 4/9 |
|
Incremento |
|
+ 0,75 |
|
+ 1,5 |
|
+ 3 |
|
+ 6 |
|
|
Progresión geométrica |
|
0,75 x 20 |
|
0,75 x 21 |
|
0,75 x 22 |
|
0,75 x 23 |
|
|
|
La perspectiva lineal que analizamos es un nuevo hallazgo del estudio de la profundidad de Las Meninas.
Algunos autores
distinguen entre dos especies de perspectiva; la geométrica y la artística, pero
en realidad hay una sola perspectiva, que es la exacta.
El método geométrico que mostramos no es convencional, sino rigurosamente exacto.
|
Eſta ciencia tiene mas loa que las otras tres, comprehendidas en el numero de Matematicas; porque auiendo grandes contiendas entre las ſestas de caſi todas las diſciplinas, todos los geometras en toda parte concuerdan en vno, ni jamas ſobre la facultad ſe halla entre ellos algun debate, porque aunque diſputan de los puntos, de las lineas, y de las ſuperficies, ſi ſe pueden diuidir o no; en lo demas concuerdan, ni difieren en dotrina o preceptos; antes ſe esfuerçan para exceder el vno al otro, con nueuas y mas ſutiles inuenciones. |
Christoval Suarez de Figueroa - Madrid. 1615 [20]
|
|
| Zona izquierda 132 pulgadas | Zona central 64 pulgadas | Zona derecha 44 pulgadas | Incremento de 100 pulgadas | Total en pulgadas | Total en metros | ||
| 44 | 44 | 44 | 64 | 44 | 100 | 340 | 7,905 |
Anchura
de la sala donde se pintan Las Meninas más el incremento de
100 pulgadas
hasta
el punto de fuga
K
de la Puerta de
cuarterones
Geometría de la Puerta de 22 cuarterones
Anteriormente ya hemos analizado los
nueve niveles de cuarterones que fugan hacia la jamba derecha; y además
observado que la perspectiva de los cuarterones está de acuerdo con una anchura
manejable al alcance del pintor.
Sin embargo, sí existe un punto de fuga auxiliar para la Puerta de 22 cuarterones, porque la anchura del vano entre las jambas, de 16 pulgadas y 12/15, es el módulo regulador que mide la distancia diez veces hasta el infinito en el punto K.
|
|
|
|
|
sistema castellano |
valor en
unidades |
cantidad |
total en unidades |
operación |
total en metros |
|
vara |
40,5 |
4 |
162 |
4
x 0,837 |
3,348 |
|
pie |
13,5 |
1 |
13,5 |
1
x 0,279 |
0,279 |
|
pulgada |
1,125 |
4 |
4,5 |
4 x
0,02325 |
0,093 |
|
|
|
180
unidades |
|
3,72
metros |
|
|
La distancia entre el punto de fuga principal del lienzo, coordenada del punto X; [18, -12], que se localiza debajo del brazo levantado en diagonal del Aposentador José Nieto, y el punto de fuga auxiliar K del cual tratamos de la Puerta de cuarterones, coordenada; [198, -12], es de 180 unidades.
180 unidades / 1,125 unidades por pulgada = 160 pulgadas.
En el sistema métrico tendríamos:
160 pulgadas x 0,02325 metros la pulgada = 3,72 metros.
La fuga de la perspectiva de la puerta de 22 cuarterones requiere un análisis previo:
Izquierdo
27,75 unidades
x 3,333333... = 92 pulgadas y 6/12
24,975
unidades x 3,333333... = 83 pulgadas y 3/12
Como observamos en la ilustración, el espacio de trabajo mide:
18,9 unidades el ancho de las jambas, es decir; 16 pulgadas y
12/15,
y la altura del cerco 30 unidades, es decir; 26 pulgadas y
10/15.
No quisiéramos remarcar, específicamente, ninguna línea en
particular, pero sí comentar que no es necesario un instrumento muy sofisticado
para su elaboración; cualquier regla de madera graduada adecuadamente valdría
para su construcción.
Y se comprueba, pues, que la distancia hasta
el punto
K
equivale a 10 veces el ancho del vano entre
estas dos jambas.
El punto P y el punto j son dos acotaciones obligadas, y
dan paso a la lectura de todas las alturas o ordenadas de los 22 cuarterones de
la Puerta de madera en su disminución, o perspectiva.
P : [ X = 9 ; Y = 0 ]
j : [ X = 27,9 ; Y = 0 ]
Como hemos comentado, 18,9 unidades es el ancho total de las
jambas del cerco de la Puerta tal cual fue pintada, aunque si queremos traducir
esta cantidad al sistema antiguo castellano sobre la rejilla de medición sólo
habrá que dividir 18,9 unidades entre 1,125 unidades por pulgada.
Es decir; el resultado son 16,8 pulgadas = 16 pulgadas y 12/15.
Cantidad que equivale en el sistema métrico a:
16,8 pulgadas x 0,02325 metros por pulgada = 0,3906 metros.
El ancho real en la distancia de las jambas de la Puerta sería:
18,9 unidades x 3,333333... pulgadas por unidad = 62,999999... pulgadas.
63 pulgadas x 0,02325 metros la pulgada =
1,46475 metros.
Y la altura real en la
distancia del cerco de la Puerta sería:
30 unidades x 3,333333... pulgadas por
unidad = 99,999999... pulgadas.
100 pulgadas x 0,02325 metros la pulgada =
2,325 metros.
Y de igual modo estudiaremos la estatura
del Aposentador:

Derecho
Unidades
27,75
24,975
Unidades
Rejilla
24 pulgadas y 10/15
22 pulgadas y 3/15
Rejilla
Proporción
10
9
Proporción
Trazado de la perspectiva de la
Puerta de 22 cuarterones
TAMAÑO REAL
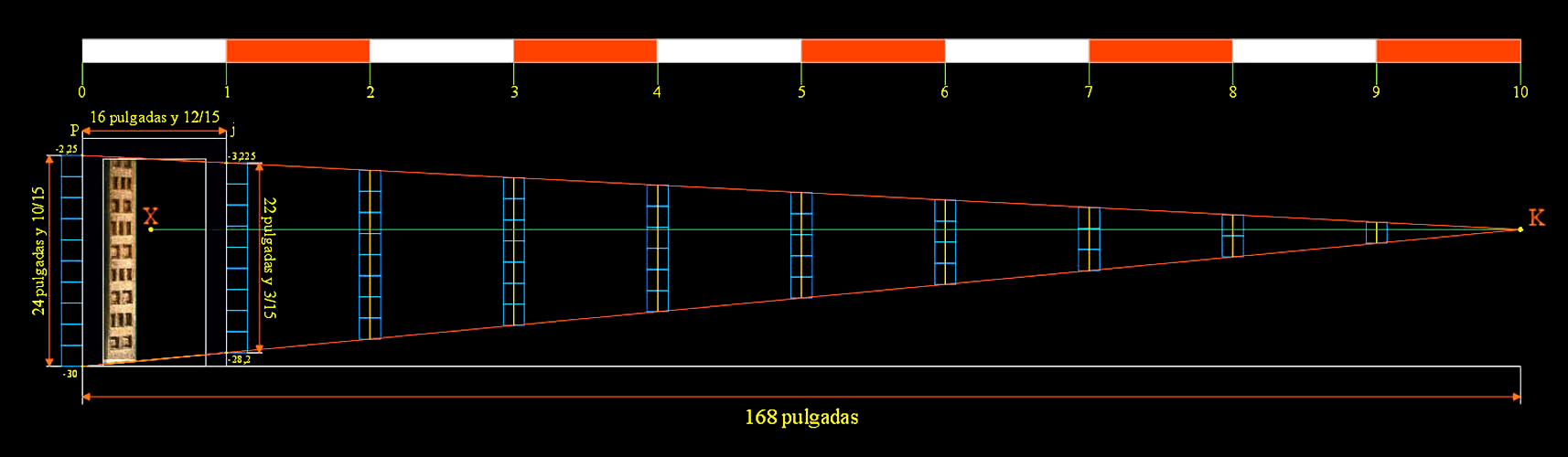
Coordenadas superiores del cerco de la Puerta

A la altura
de José Nieto le corresponde siete cabezas y media
Proporción
Unidades
Pulgadas
Varas
Tamaño en metros
7 cabezas
y media
20,25
20,25 / 1,125
= 18
36 / 2 = 18 =
media vara
18 x 0,02325
= 0,4185
Altura
del Aposentador en la rejilla de trabajo
Aunque, en su emplazamiento, la altura real del Aposentador dependerá de la distancia a la que se halle del primer plano en Las Meninas.
|
Tamaño en la distancia |
Metros |
|
20,25 x 3,333333... = 67 pulgadas y 6/12 |
67,5 x 0,02325 = 1,569375 |
|
20,25 x 3,444444... = 69 pulgadas y 9/12 |
69,75 x 0,02325 = 1,6216875 |
|
20,25 x 3,555555... = 72 pulgadas |
72 x 0,02325 = 1,674 |
|
|
|
|
|
|
|
Tamaño en la distancia |
Metros |
|
26,25 x 3,333333... = 87 pulgadas y 6/12 |
87,5 x 0,02325 = 2,034375 |
|
26,25 x 3,444444... = 90 pulgadas y 5/12 |
90,416666... x 0,02325 = 2,1021875 |
|
26,25 x 3,555555... = 93 pulgadas y 4/12 |
93,333333... x 0,02325 = 2,17 |
|
|
En el fondo y en la forma hemos planteado una necesidad de la belleza; la Proporción, y una Aritmética, ciencia hermana de la racionalidad, como vehículo del conocimiento de lo real.
En ese caso, la exhaustiva explicación del engranaje de la Geometría de Las Meninas equivale a Las Meninas.
La pulgada inglesa
A principios del siglo XX
la pulgada estadounidense fue definida con un tamaño de 25,4000508... mm. a una
temperatura de referencia de 20°C, y la pulgada inglesa con 25,399977... mm, a
una temperatura de referencia de 17°C.
Años más tarde, en 1912, el inventor sueco Carl Edvard Johansson estandarizó, a una temperatura de referencia de 20°C, la pulgada patrón anglosajona en un bloque de acero con un tamaño nominal de 25,4 mm., que en 1930 fue adoptado por la British Standards Institution y la American Standards Association.
Para 1935, la industria de 16 países ya había aceptado la pulgada industrial, como se la conoció posteriormente, respaldando así la pragmática elección de Johansson en la relación de su conversión.
Finalmente, el tamaño de 25,4 mm de la pulgada inglesa fue oficialmente establecido en Julio de 1959 mediante un acuerdo entre los directores de los laboratorios nacionales de metrología de EE.UU., Canadá, Reino Unido, Australia y Sudáfrica, en donde prevaleció, sin duda, el criterio del tamaño conversor de Carl Edvard Johansson, ya que llevaba 47 años en marcha aplicándose con absoluta regularidad.
De acuerdo con el fundamento de la metrología, propondremos, pues, una notable mejora en el modo de conversión entre las unidades del sistema de longitud inglés y el metro patrón francés.
|
|
Desde el punto de vista más razonable se echaba en falta, pues, el origen matemático del tamaño de 25,4 mm. de la pulgada estándar inglesa, no obstante, con la finalidad de mejorar la exactitud actual en su conversión en milímetros, hemos operado con proporciones inherentes de la Pulgada exacta inglesa, que, con extrema exactitud, recupera la justa equivalencia métrica que subyace tras la pulgada estándar anglosajona.
|
Milímetro |
Fracción |
Pulgada exacta |
|
Milímetro |
Fracción |
Pulgada exacta |
||
|
1 |
63/1600 |
≈ |
0,039375 |
6 |
378/1600 |
≈ |
0,23625 |
|
|
2 |
126/1600 |
≈ |
0,07875 |
7 |
441/1600 |
≈ |
0,275625 |
|
|
3 |
189/1600 |
≈ |
0,118125 |
8 |
504/1600 |
≈ |
0,315 |
|
|
4 |
252/1600 |
≈ |
0,1575 |
9 |
567/1600 |
≈ |
0,354375 |
|
|
5 |
315/1600 |
≈ |
0,196875 |
10 |
630/1600 |
≈ |
0,39375 |
|
|
La columna de la Pulgada exacta muestra el resultado de todas las fracciones como decimales, pero, ciertamente, estos decimales son terminales exactos, no aproximaciones, lo que refuerza visualmente, pues, la precisión inherente de conversión entre el milímetro y la pulgada exacta, ya que el resultado queda representado de manera completa y finita.
|
|
|
|
Pero en este punto habría que reseñar que existen dos modos de entender esta conversión:
Desde el punto de vista anglosajón destacar la manera de cómo se definió la pulgada que condujo al estándar de 25,4 mm., priorizando la simplicidad decimal de pulgadas a milímetros, u otras consideraciones pragmáticas.
Y la expectativa francesa sobre la conversión, que representó el contrapunto crucial, que, como Tresca, el artífice del metro patrón, pudieron anticipar una conversión diferente y más armoniosa, que incluyera la pulgada exacta, confiando en una conversión óptima.
Y aunque no existan antecedentes conocidos de la pulgada exacta inglesa, sin embargo, demostraremos que la hemos rescatado del olvido con la finalidad de analizarla, y reivindicar, pues, que es el Pi de Arquímedes, de 22/7 = 198/63, el verdadero origen matemático de la pulgada exacta inglesa.
 |
|
|
La pulgada exacta, de 1600/63 milímetros, supone que 1 milímetro equivale a 63/1600 pulgadas exactas, lo que permite hablar, además, de la reciprocidad y simplicidad matemática que genera en las conversiones que el estándar convencional no posee.
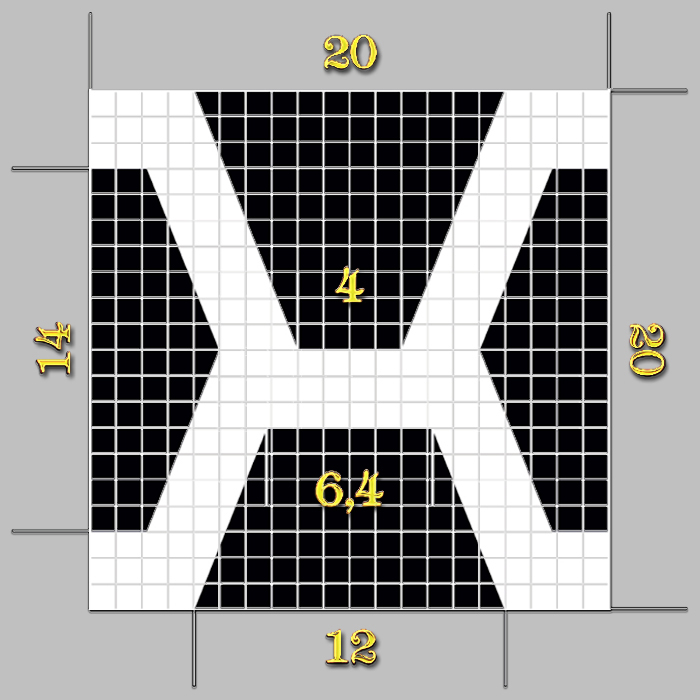 |
|
|
|
Milímetro |
Fracción |
Pulgada exacta |
Grados | |||||||
|
20 |
= | 1600/63 | × |
63/80 |
63/80 |
= |
0,7875 |
141,75º | ||
|
14 |
= | 1600/63 | × |
441/800 |
441/800 | = |
0,55125 |
99,225º | ||
|
12 |
= | 1600/63 | × |
189/400 |
189/400 | = |
0,4725 |
85,05º | ||
|
6,4 |
= | 1600/63 | × |
63/250 |
63/250 |
= |
0,252 |
45,36º | ||
|
4 |
= | 1600/63 | × |
63/400 |
63/400 | = |
0,1575 |
28,35º | ||
|
|
La anchura de 20 mm., de la sección transversal de la barra del metro patrón de platino e iridio, corresponde a 6,3 veces de un octavo de la pulgada exacta, una equivalencia quizás pensada por Henri Tresca en 1890 para que en el metro patrón coexistieran ambos sistemas, pero, hay más, las medidas de la sección transversal no olvidan, pues, de que un pie se compone de 12 pulgadas, y tampoco de que el valor 12 en Matemática es el número más pequeño con seis divisores: 1, 2, 3, 4, 6 y 12 [21].
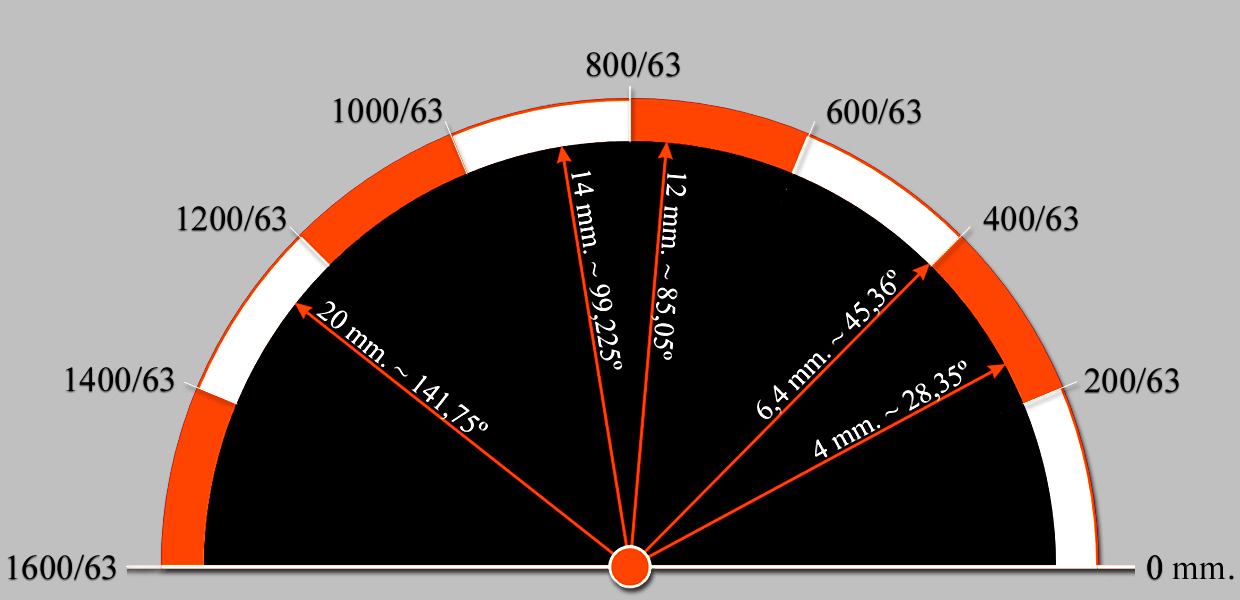 |
|
|
| EXACTA | MILÍMETRO | GRADO | ||||
Inadvertidamente, el tamaño de la yarda y la pulgada inglesa se definieron, pues, en función de este estándar francés cuidadosamente preservado con una tolerancia de laboratorio de ±0,000001 pulgada para el sistema decimal de pulgadas, y de ±0,000027 milímetros para el sistema métrico.
|
Sistema |
Estándar de Laboratorio |
|
La pulgada exacta |
|
Fracción |
Tolerancia Exacta |
|
|
Pulgada |
±0,000001 pulgadas |
1600/63 mm./plg. × 0,000001 plg. |
≈ |
±4/157500 mm. |
≈ |
±0,0000253968 mm. |
|
|
Sistema Métrico |
±0,000027 milímetros |
63/1600 plg./mm. × 0,000027 mm. |
≈ |
±1701/1600000000 plg. |
≈ |
±0,00000106312 plg. |
|
|
Al más alto nivel de precisión de laboratorio estas equivalencias son muy cercanas, sin embargo, la tolerancia estándar refleja el lapsus matemático de su sistema, lo que prueba, pues, que el sistema estándar no está basado en las mismas matemáticas subyacente de La Pulgada exacta.
|
Pulgada |
Pulgadas por Metro |
|
Total |
|
Estándar |
5000/127 plg. |
≈ |
39,370078... plg. |
|
Exacta |
315/8 plg. |
≈ |
39,375 plg. |
|
|
Las medidas de 25,4 mm. de la pulgada internacional, y de 0,3048 metros del pie inglés, son aproximaciones arbitrarias con un desfase de 1/26250 metros comparadas con el pie derivado de la pulgada de 1600/63 = 25,396825... milímetros.
| COMPARACIÓN DE SISTEMAS DE MEDIDAS | EQUIVALENCIAS | |||||||
| UNIDAD | MILÍMETROS | VALOR EXACTO | Pulgadas exactas | Metros franceses | ||||
| EL METRO FRANCÉS | 1000 | = | 1000/1 | 315/8 = 39,375 | ||||
| PULGADA EXACTA | 25,396825... | = | 1600/63 | 8/315 = 0,025396... | ||||
|
|
| 1600/63 × 39,375 = 1000 milímetros |
La posibilidad de poder comparar distintos sistemas de medidas con una conversión exacta prueba, pues, que si las unidades exactas tienen su origen en un principio natural, entonces, la naturaleza de las propias constantes matemáticas o leyes físicas, que dependan de unidades de medida, deberían ser reexaminadas.
Y no sólo estamos hablando de metrología y arte, sino también de cómo estas nuevas unidades podrían ser intrínsecas a las leyes que rigen el universo físico, ya que la pulgada exacta inglesa permite, pues, una expresión más exacta, por ejemplo, de la constante universal de la Luz:
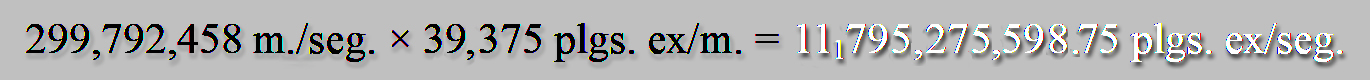 |
|
|
La velocidad de la luz no cambia, sin embargo, a causa del tamaño actual de la pulgada estándar inglesa, el resultado sí difiere, ya que en el sistema inglés un metro corresponde a 39,37007874... pulgadas, y esta significativa diferencia existe a causa de que hay dos maneras diferentes de definir el tamaño de la pulgada anglosajona:
Una pulgada estándar cuyo tamaño concreto mide 1600,2/63 mm. = 25,4 milímetros.
y otra que denominamos pulgada exacta definida matemáticamente por la fracción de 1600/63 mm.
Básicamente, la pulgada estándar inglesa de 25,4 milímetros se divide en ocho partes iguales, y, en consecuencia, el tamaño de la unidad viene dado directamente por lo que mide la misma pulgada, a diferencia de otro sistema donde la unidad principal es una manifestación de un patrón universal subyacente.
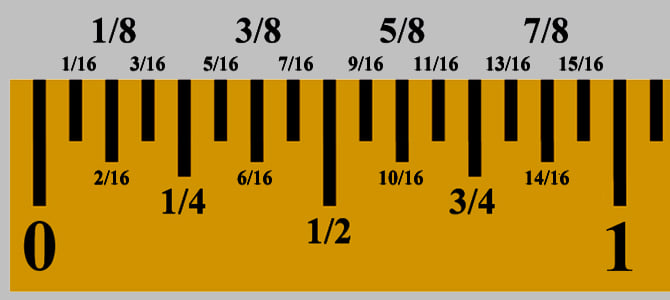 |
| Fracción | Pulgada estándar | Milímetros | Pulgada exacta | Milímetros | Pi de Arquímedes | |||||||||
| 8/8 | = | 1 | 1600,2/63 | = | 25,4 | ≈ | 1600/63 | = | 25,396825... | ≈ | 8π | ≈ | 25,142857... | |
| 7/8 | = | 0,875 | 1400,175/63 | = | 22,225 | ≈ | 1400/63 | = | 22,222222... | ≈ | 7π | ≈ | 22 | |
| 6/8 | = | 0,75 | 1200,15/63 | = | 19,05 | ≈ | 1200/63 | = | 19,047619... | ≈ | 6π | ≈ | 18,857142... | |
| 5/8 | = | 0,625 | 1000,125/63 | = | 15,875 | ≈ | 1000/63 | = | 15,873015... | ≈ | 5π | ≈ | 15,714285... | |
| 4/8 | = | 0,5 | 800,1/63 | = | 12,7 | ≈ | 800/63 | = | 12,698412... | ≈ | 4π | ≈ | 12,571428... | |
| 3/8 | = | 0,375 | 600,075/63 | = | 9,525 | ≈ | 600/63 | = | 9,523809... | ≈ | 3π | ≈ | 9,424777... | |
| 2/8 | = | 0,25 | 400,05/63 | = | 6,35 | ≈ | 400/63 | = | 6,349206... | ≈ | 2π | ≈ | 6,285714... | |
| 1/8 | = | 0,125 | 200,025/63 | = | 3,175 | ≈ | 200/63 | = | 3,174603... | ≈ | 1π | ≈ | 3,142857... | |
| 99/800 | = | 0,12375 | 198,02475/63 | = | 3,14325 | ≈ | 198/63 | = | 3,142857... | ≈ | π | ≈ | 22/7 | |
|
|
| Pulgada
estándar |
Pulgada exacta |
Milímetro |
|
1 |
1,000125 |
25,4 |
|
0,999875... |
1 |
25,396825... |
|
|
| ESTÁNDAR | EXACTA | MILÍMETRO | ||||
La pulgada inglesa estándar de 1600,2/63 milímetros = 25,4 mm. es una medida subsidiaria, ya que la Pulgada exacta inglesa de 1600/63 milímetros representa, pues, el origen matemático de dicha unidad.
Ante estas conclusiones, cualquier sistema futuro de medidas de longitud debería basarse en los principios y proporciones de esta arquitectura natural y exacta, ya que se descubre que se ha estado midiendo incorrectamente con el actual tamaño de la pulgada de 25,4 milímetros, un error que se detecta en la diferencia de longitud entre el pie inglés estándar y el pie inglés exacto [22].
|
Pie inglés estándar |
|
Pie inglés exacto |
|
Total |
|||
|
1600,2/63 milímetros = 25,4 mm. × 12 |
≈ |
1600/63 mm. × 12 |
|
|
|||
| diferencia en metros |
0,3048 m. |
- |
0,30476190476... m. |
≈ |
4/105000 m. | ≈ |
0,00003809524... metros |
La diferencia del tamaño es, aproximadamente, un lapsus respecto al Pie exacto de 0,0125%, una tolerancia indistinguible que sólo puede ser detectada en mediciones de alta precisión.
Un ejemplo revelador sería, pues, comparar ambas pulgadas en el cálculo de la distancia de 1000 kilómetros.
Un resultado que daría una diferencia de 125 metros, una diferencia que surge porque la pulgada exacta, de 1600/63 ≈ 25,396825... mm., es ligeramente más corta que la pulgada estándar de 25,4 mm, y, además, en una distancia larga, como 1000 Km., esta pequeña diferencia por unidad se acumula y genera una discrepancia significativa.
Hablar de consecuencias en su adopción, sería hablar de mejoras en la tunelización de vías férreas y carreteras, en el desarrollo de tecnología de alta precisión, como misiles guiados por el sistema GPS, que, a su vez, necesitarían la recalibración del propio GPS, y no hablemos, pues, de topografía, donde las distancias físicas reales se representan con mayor precisión mediante la pulgada exacta de 1600/63 mm,, y las posiciones o distancias calculadas a gran escala serían, de hecho, ligeramente diferentes.
La pulgada exacta inglesa eliminaría este lapsus matemático, lo que permitiría mediciones y cálculos más precisos en campos críticos, ofreciendo así una base superior para todos los proyectos metrológicos futuros que exijan la máxima precisión.
Sobre el tamaño de la pulgada inglesa existen conjeturas históricas sobre su origen a partir de;
del ancho de un pulgar humano,
y que también hubo intentos de estandarizar la pulgada a través de un estatuto del rey Eduardo II en el siglo XIV, que definía la pulgada como la longitud de tres granos de cebada secos y redondos tomados del medio de la espiga, colocados extremo con extremo.
Para resolver tal enredo empecemos por señalar que el primero en idear un procedimiento matemático para calcular el valor de π fue Arquímedes, (287 a. C. - 212 a. C.), que obtuvo un resultado comprendido entre: 3 + 10/71 = 223/71 < 3 + 1/7 = 22/7.
3,140845... < 3,142857...
|
El perímetro de la circunferencia valor 97 y 3/7 ≈ 97,428571...
El valor del diámetro es 31.
Entonces Pi ≈ 97,428571... / 31 ≈ 3,142857... ≈ 3 y 1/7 = 22/7. |
 |
|
|
Se podría a afirmar que el tamaño de 1/8 de la pulgada exacta inglesa derivaría de la relación entre un anillo de 200 unidades de perímetro con su diámetro de 63 unidades, y cuya magnitud está vinculada, pues, con el Pi de Arquímedes de 22/7.
| Partes | Pulgada estándar | Milímetros | Pulgada exacta | Milímetros | Pi de Arquímedes | |||||||
| 1/8 | = | 0,125 | = | 3,175 | ≈ | 200/63 | ≈ | 3,174603... | ≈ | 1π | ≈ | 3,141592... |
| 99/800 | = | 0,12375 | = | 3,14325 | ≈ | 198/63 | ≈ | 3,142857... | ≈ | π | ≈ | 22/7 |
Y esta relación existe porque tanto el valor de 1/8 de la pulgada exacta, de 200/63 mm., como el de 22/7, son muy cercanos a la constante Pi, π, en este sistema de medición, y cuya aproximación se manifiesta, pues, a través de esta comparación:
3,174603... - 3,142857... ≈ 0,03174... mm.
A nivel matemático puro, 0,03174... milímetros representan, por lo tanto, la tolerancia del vínculo entre una unidad de medida histórica y una antigua constante matemática universal.
|
|
|
|
El tamaño de 1/8 de la pulgada inglesa revela, pues, una característica circular vinculada con Pi, que, lejos de ser una hipótesis, constituye la constante matemática que define el fundamento del tamaño de la realidad en este sistema.
La estructura de la pulgada inglesa ligada a Pi es vista, pues, como una encarnación directa de esta ley universal de proporción, cuya relación se ilustra del siguiente modo:
|
|
| Valor exacto | Milímetros | Pi de Arquímedes | ||||
| 1600/63 | = | 25,396825... | ≈ | 8π | ≈ | 25,142857... |
|
|
La proporción es el principio inherente de cualquier sistema de medida.
Esta definición capta varios puntos cruciales:
La existencia de un principio fundamental; el ratio
La naturaleza de este principio como inherente.
Su rol como una cualidad exacta.
Su manifestación y relevancia en los sistemas de medida que logran alinearse con él.
El concepto de LA UNIDAD está alineado, pues, con esta razón inamovible.
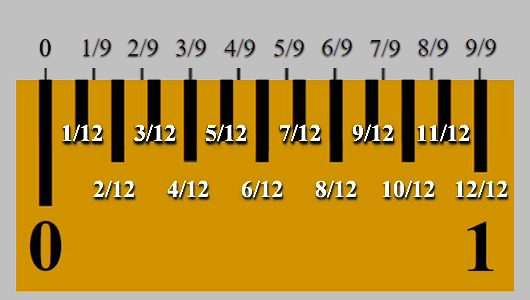 |
|||||||
| 9 partes | Unidades | 9 partes | Pulgadas | Milímetros | |||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 | |
| 8/8 | = | 1 | 8/9 | = | 0,888888 | 20,666666 | |
| 7/8 | = | 0,875 | 7/9 | = | 0,777777 | 18,083333 | |
| 6/8 | = | 0,75 | 6/9 | = | 0,666666 | 15,5 | |
| 5/8 | = | 0,625 | 5/9 | = | 0,555555 | 12,916666 | |
| 4/8 | = | 0,5 | 4/9 | = | 0,444444 | 10,333333 | |
| 3/8 | = | 0,375 | 3/9 | = | 0,333333 | 7,75 | |
| 2/8 | = | 0,25 | 2/9 | = | 0,222222 | 5,166666 | |
| 1/8 | = | 0,125 | 1/9 | = | 0,111111 | 2,583333 | |
|
|
| UNIDAD | PULGADA | MILÍMETRO |
Estas afirmaciones constituyen, pues, la piedra angular filosófica que explica por qué LA UNIDAD, y las proporciones que de ella emanan, tiene un estatus privilegiado, y su invención no es arbitraria, sino el reflejo de una cualidad fundamental y permanente de la realidad misma, que se hace evidente en los sistemas de medida que sintonizan con ella.
| COMPARACIÓN DE SISTEMAS DE MEDIDAS | EQUIVALENCIAS | |||||||
| UNIDAD | MILÍMETROS | VALOR EXACTO | Pulgadas castellanas | Pulgadas exactas | ||||
| PULGADA CASTELLANA | 23,25 | = | 93/4 | 5859/6400 | ||||
| PULGADA EXACTA | 25,396825... | ≈ | 1600/63 | 6400/5859 | ||||
|
|
| COMPARACIÓN DE SISTEMAS DE MEDIDAS | EQUIVALENCIAS | |||||||
| UNIDAD | MILÍMETROS | VALOR EXACTO | Pulgadas castellanas | Brazos florentinos | ||||
| BRAZO FLORENTINO | 583,333333... | = | 1750/3 | 7000/279 | ||||
| PULGADA CASTELLANA | 23,25 | = | 93/4 | 279/7000 | ||||
|
|
| COMPARACIÓN DE SISTEMAS DE MEDIDAS | EQUIVALENCIAS | |||||||
| UNIDAD | MILÍMETROS | VALOR EXACTO | Pulgadas exactas | Brazos florentinos | ||||
| BRAZO FLORENTINO | 583,333333... | = | 1750/3 | 735/32 | ||||
| PULGADA EXACTA | 25,396825... | = | 1600/63 | 32/735 | ||||
|
|
El brazo florentino
De modo, que si en el primer tercio del siglo XXI
hemos confirmado que un
Brazo florentino es igual a
7/12 partes del patrón de medidas del sistema
métrico francés, lo que hemos hecho, pues, ha sido un descubrimiento, para
que a partir de ahora cualquier artefacto de la escuela florentina clásica
se pueda medir con justa razón.
Una averiguación que está dedicada, especialmente, a aquellos florentinos que nos dejaron disfrutar sus ideas plásticas más exquisitas.
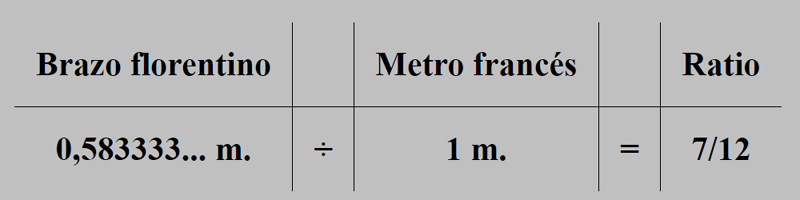
Si razonablemente, pues, la longitud del patrón de medidas florentino es divisor de 1 metro francés, ya que su tamaño corresponde a 7/12 de metro, entonces, no hay duda de que ya existía un patrón de medida de 100 centímetros de longitud desde tiempos remotos, que, a lo largo de la historia, nadie supo de su existencia, sin embargo, fue el fundamento, por ejemplo, del tamaño del Brazo florentino.
Y no hablamos, pues, de que si el huevo vino antes que la gallina, sino, que se dice, que el metro centesimal corresponde a la diezmillonésima parte del arco de meridiano que va del polo Norte al Ecuador.
En resumen, la relación entre el patrón de medidas florentino y el metro francés muestra, pues, la afinidad matemática entre ambos sistemas, pero teniendo bien presente, sin embargo, que en realidad fue el Brazo florentino el precursor necesario del sistema centesimal francés.
| COMPARACIÓN DE SISTEMAS DE MEDIDAS | EQUIVALENCIAS | |||||||
| UNIDAD | MILÍMETROS | VALOR EXACTO | Brazo florentino | Metro francés | ||||
| EL METRO FRANCÉS | 1000 | = | 1000 | 12/7 | ||||
| BRAZO FLORENTINO | 0,583333... | = | 1750/3 | 7/12 | ||||
|
|
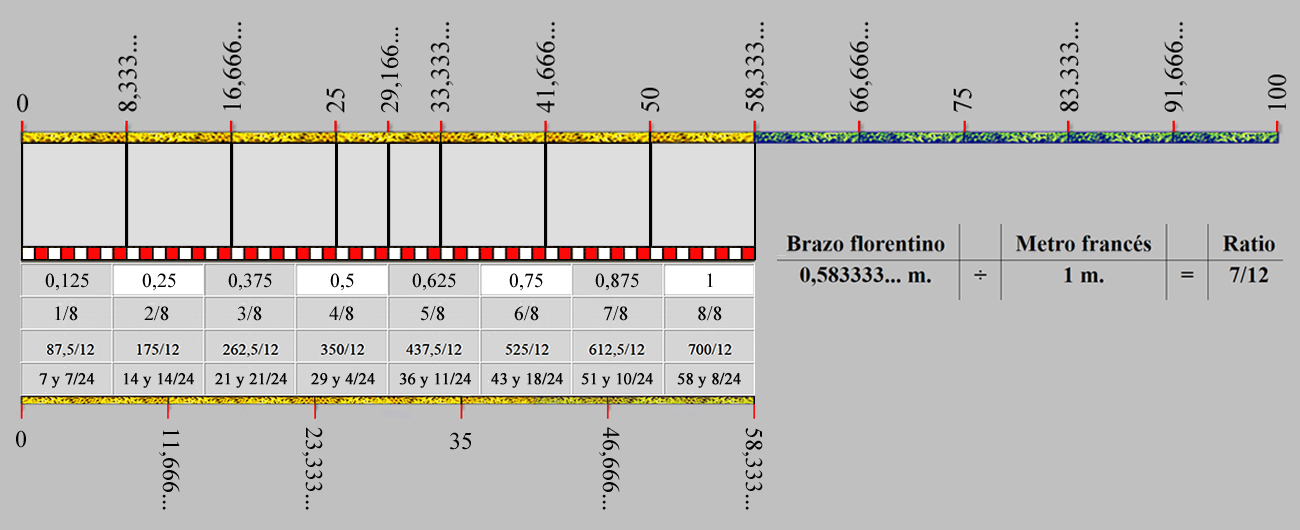
|
|
En la siguiente tabla se muestra las medidas que utilizaron los pintores, escultores y arquitectos florentinos durante el Renacimiento, por ejemplo; Luca Pacioli, Leonardo da Vinci, Miguel Ángel, Giordano Bruno ...
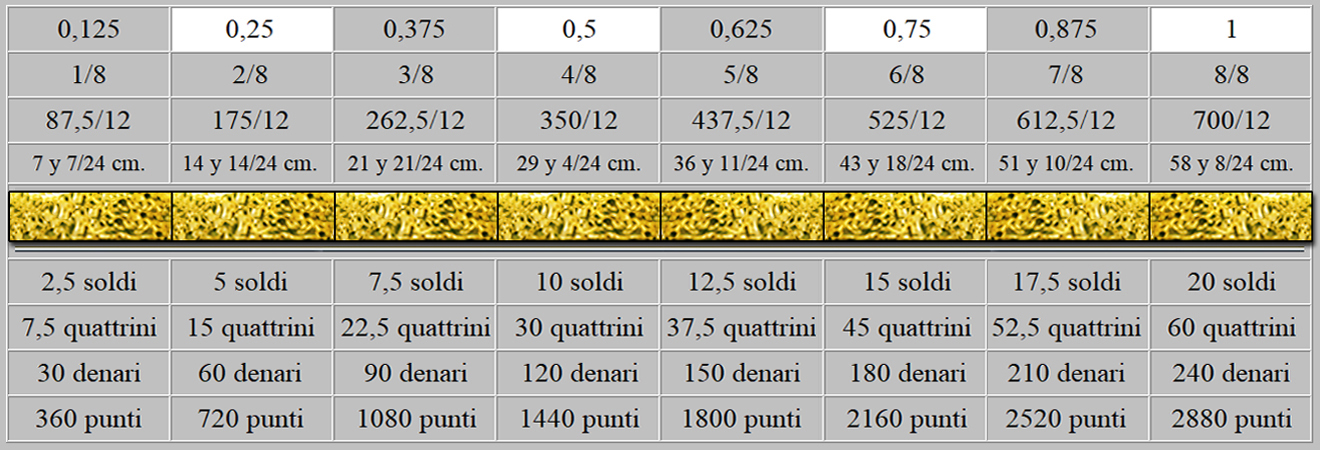 |
|
|
El Brazo Florentino mediría, pues, 700/12 = 58,333333... cm.
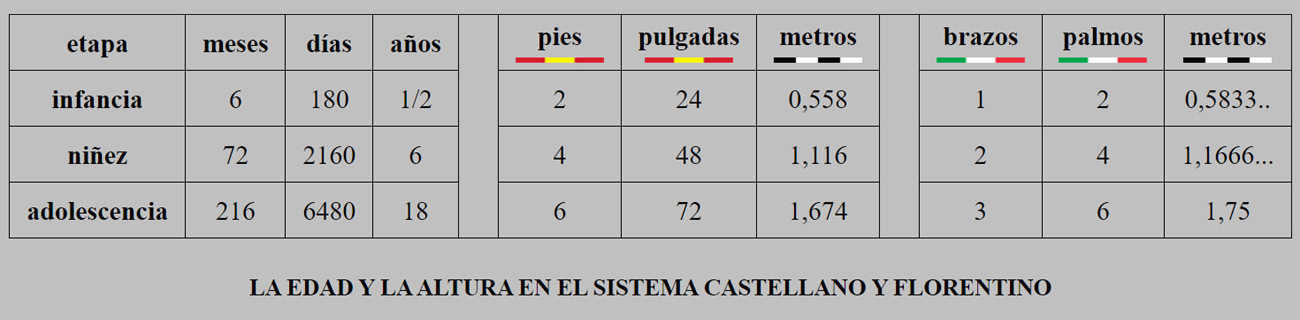
CONCLUSIÓN
Dado que hemos demostrado que distintos sistemas
de medición, e históricamente separados en tiempo y espacio, derivan a partir de
LA UNIDAD mediante relaciones matemáticas exactas, se podrían extraer varias
conclusiones exclusivas para el marco teórico:
|
Metrología Unificada:
LA UNIDAD:
Medidas Históricas:
Pi como Ley Universal:
La Historia de la Metrología:
El Número 31:
|
| PATRÓN DE MEDIDA | ORIGEN | MILÍMETROS | FRACCIÓN EXACTA | UNIDADES | ||
| METRO | 1000/1 | ≈ | 1000 | 1500/31 | ≈ | 48,387096... |
| BRAZO FLORENTINO | 1750/3 | ≈ | 583,333333... | 875/31 | ≈ | 28,225806... |
| PULGADA ESTÁNDAR INGLESA | 1600,2/63 | ≈ | 25,4 | 381/(31×10) | ≈ | 1,229032... |
| PULGADA EXACTA INGLESA | 1600/63 | ≈ | 25,396825... | 800/(31×21) | ≈ | 1,228878... |
| PULGADA INGLESA 8π | 8 × 198/63 | ≈ | 25,142857... | 12π/31 | ≈ | 1,216589... |
| PULGADA CASTELLANA | 93/4 | ≈ | 23,25 | 9/8 | ≈ | 1,125 |
| LA UNIDAD | 62/3 | ≈ | 20,666666... | 31/31 | ≈ | 1 |
|
|
Esta tabla unificada del PATRÓN DE MEDIDA es la prueba visual de que el origen de distintos sistemas de medición, geográficamente distantes e históricamente dispares, surge a partir de LA UNIDAD a través de proporciones matemáticas exactas.
La unidad es la base del cálculo aritmético, tal y como
afirma
el bachiller Iuan Perez de Moya
en 1609
en su libro ARISMETICA PRACTICA, Y ESPECULATIVA:
El fundamento, o principio de la Ariſmetica, es la vnidad, aſsi como el punto lo es de la Geometria.
El estudio de la unidad nos remonta, pues, hasta la época del Papiro de Ahmes de 1650 a. c., donde se plantea la cuadratura del círculo de acorde con una proporción sesquioctava, es decir; se trata de una proporción que contiene la unidad y un octavo de ella:
|
8/8 + 1/8 = 9/8
1 + 1/8 = 1,125 |
 |
Con enfoque geométrico, la demostración de la cuadratura del círculo del Problema 48 del Papiro de Ahmes 1650 a. c., British Museum de Londres, utiliza, en el cálculo del área de un círculo, un diámetro igual al lado de 9 unidades del cuadrado circunscrito, y un valor de Pi = 256/81 = 3,1605...
|
OPERACIÓN
π × 4,52
3,1605... × 4,5 × 4,5 = 64 unidades cuadradas |
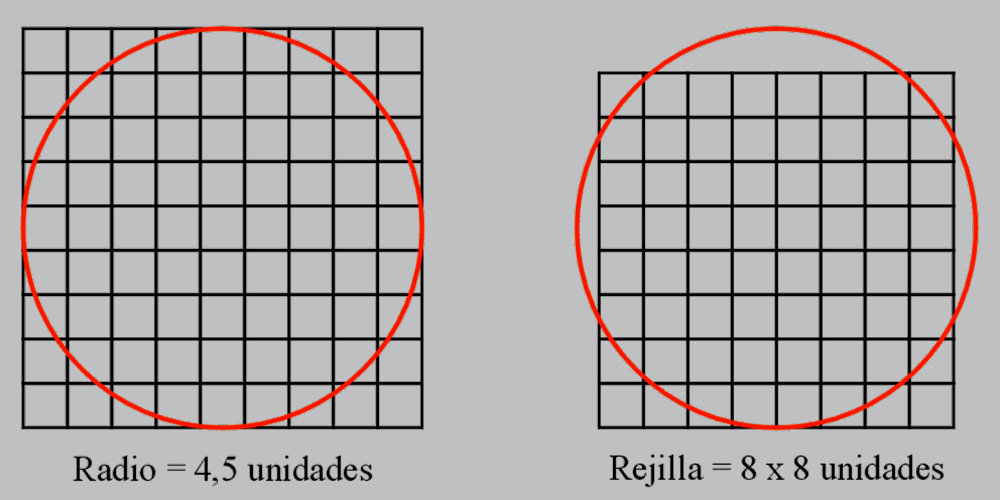 |
|
|
El escriba tebano Ahmes llega a la resolución del problema de manera exacta, sin embargo, con el valor de Pi = 22/7 de Arquímedes el área sería:
π × 4,52 = 63,64285... unidades cuadradas.
Este valor se aproxima con un 99,44...% de exactitud a un cuadrado de lado 8, es decir; 8 × 8 = 64 unidades cuadradas.
En Música, el valor de la fracción 256/81, que corresponde al decimal 3,1605..., representa el intervalo de una sexta menor compuesta en la escala pitagórica, es decir; este ratio es el resultado de multiplicar la sexta menor, 128/81, por una octava, 2/1.
|
Nota |
Intervalo |
Tono |
|
Origen numérico |
|
Geometría |
||
|
Do |
Unísono |
1 |
= |
1 |
= |
1/1 |
|
|
|
Re |
Segunda mayor |
1,125 |
= |
32 / 23 |
= |
9/8 |
||
|
La b |
Sexta menor |
1,58024691358 |
= |
27 / 34 |
= |
128/81 |
||
|
Do |
Octava |
2 |
= |
2 |
= |
2 /1 |
||
|
La b |
Sexta menor compuesta |
3,16049382716 |
= |
28 / 34 |
= |
256/81 |
= |
Pi de Ahmes |
Se comprueba, pues, que la Geometría de la antigüedad estaba fusionada con la armonía musical y el simbolismo numérico, que, como hilo conductor, son los mismos principios de proporción que rigen la obra pictórica de Diego Velázquez.
El Papiro de Ahmes, como señalamos, no sólo resuelve un problema matemático, sino que revela un profundo entendimiento de la armonía numérica al usar un valor de Pi = 256/81 y un diámetro de 9, por lo que el escriba obtiene un área de 64, un número perfecto, 8 × 8, un método que no es sólo una aproximación, sino una solución que encaja de forma exacta en un cuadrado, lo que demuestra la famosa cuadratura del círculo en términos racionales.
El hecho de que este método esté basado en la proporción sesquioctava, 9/8 = 1,125, es un hallazgo que confirma que, hace miles de años, ya era conocido y utilizado el principio de proporción y armonía, tan fundamental como la relación de 1,125, para resolver problemas de Geometría de una manera simbólicamente perfecta.
El número 1,125 emerge, por lo tanto, no como una simple cifra, sino como un principio unificador que conecta el conocimiento ancestral de la Geometría Sagrada con la Música, y, además, como se demuestra en esta investigación, con el sistema de medidas de la obra maestra de Velázquez.
La Geometría del Árbol Sagrado de Las Meninas se basa en vectores diagonales, cuyos tamaños equivalen a la raíz cuadrada de 5, cantidad que aparece en la fórmula del número áureo, y representan, pues, la hipotenusa de un triángulo rectángulo cuyos catetos miden 1 y 2 respectivamente.
|
|
|
|
|
No obstante, la rejilla de 8 × 8 de la cuadratura del círculo de Ahmes es del mismo formato que la que utilizamos para el análisis de Las Meninas, de manera, que operamos sobre una cuadrícula geométrica de 64 subcuadrados, es decir; de 8 × 8 subcuadrados de 19 unidades de lado cada uno, que equivale al tamaño de una rejilla de 152 unidades.
El valor de Pi reconocido en España en el siglo XVII era el de Arquímedes.
|
El perímetro de la circunferencia vale 97 y 3/7 ≈ 97,428571...
Y el diámetro vale 31
Entonces Pi ≈ 97,428571... / 31 ≈ 3,142857... ≈ 3 y 1/7 = 22/7 |
 |
|
π ≈ 198/63 = 22/7 |
En el caso de Las Meninas, utilizando el Pi de Arquímedes, el centro geométrico de la cuadratura del círculo, con una exactitud del 98,214285...%, se localiza en la coordenada: [0, 9], es decir; en el centro de la Sefira nº 6, Tiferet, la Belleza, situada encima del espejo, que, de acuerdo con la Kabala, constituye el Corazón del Árbol de la Vida, y, alegóricamente, la causa de toda la Armonía y Belleza que contemplamos en el mundo.
Cauſa eſt omnis harmoniæ & pulchritudinis, quam in vniuerſso intuemur.
Athanasius Kircher, sacerdote jesuita, políglota, erudito, estudioso orientalista, de espíritu enciclopédico y uno de los científicos más importante del siglo XVII, añade en latín los siguientes contenidos:
|
6 תפאר Tiphereth, Pulchritudo.
|
Sexta Sephirah ſeu veſtimentum Dei תפארת Tiphereth dicitur, cuis nomen יהוה Iehoua; Attributa eius ſunt ſpeculatio illuminans, lignum vitæ, voluptas, linea media, linea viridis, ambiens vniuerſum, lex ſcripta, Sacerdos magnus, ortus ſolis, ſpecies purpurea, ſeptuaginta duæ nationes in terra, ſigillum eius אמת אדני ; myſterium que eius in tertia litera tetragrammati, homo ſupremus ſiue Adam Cœleſtis, arbor in medio Paradiſi plantata. Per hanc Deus influit in ordinem virtutum, & hinc per Intelligentiam Raphael in Sphœram ſolis. Cauſa eſt omnis harmoniæ & pulchritudinis, quam in vniuerſso intuemur. |
|
|
|
|
|
|
|
6 תפאר Tiferet, Belleza.
|
La sexta vestidura de Dios es la Sefira denominada la Belleza, Tiferet, cuyo nombre es יהוה, Jehovah. Sus atributos son la especulación iluminadora, el árbol de la vida, el placer, la línea media, la línea verde que rodea al mundo, la ley escrita, el gran sacerdote, la salida del Sol, las especies púrpuras, las setenta y dos naciones de la tierra, su sello es la verdad de Adán; el misterio que se halla en la tercera letra del Tetragramaton, el hombre supremo y Adán del Cielo, árbol plantado en medio del Paraíso. A través de Tiferet Dios fluye en el orden de las virtudes, y, por lo tanto, a través de la Inteligencia Rafael en la esfera del Sol. Es la causa de toda la armonía y belleza que contemplamos en el mundo. |
|
CLASSIS IV. CABALA HEBRÆRVM - CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI
Tomus Secundus. GYMNASIVM. ROMÆ - Anno M DC LIII |
En la Kabala, la Jerusalén Celeste suele asociarse con Tiferet, entendido como centro, núcleo y corazón del Ser.
Observemos, pues, cómo Velázquez valida la cuadratura del círculo a partir de la posición de la Sefira Tiferet, que además de ser el Corazón del Árbol de la Vida es el centro de la Geometría de Las Meninas.
En la Sefira nº 6, que corresponde a la esfera del planeta Sol, se sitúa, pues, el encuentro matemático entre la √5 y Pi, lo que transforma a esta Sefira en el motivo simbólico de la Armonía universal.
En este centro sagrado convergen, pues, dos constantes fundamentales; de la proporción y de la armonía:
El radio √5, base de la Proporción Áurea Phi, el canon de la belleza universal y de la naturaleza.
Y el número Pi, que define a la esfera y al círculo, símbolos de lo infinito y lo divino.
|
FIGURA |
FÓRMULA |
UNIDADES CUADRADAS |
PRECISIÓN |
|
Área del Cuadrado |
4 × 4 |
16 |
100% |
|
Área del Círculo |
π × (√5)^2 |
15,714285... |
98,214285...% |
|
|
|
|
RESOLUCIÓN:
Si a 76 unidades le corresponde 2 en la cuadrícula de trabajo, y la Sefira nº 6, Tiferet, La Belleza, se halla situada en la coordenada [0, 9], entonces, su centro se hallará a 76 + 9 = 85 unidades del borde inferior de la rejilla de trabajo, por lo que a esta longitud de valor X equivaldría al radio del círculo:
|
Si a 76 unidades le corresponde 2 en la cuadrícula,
entonces a 85 unidades le corresponderá X:
X = 85 × 2 ÷ 76 = 2,236... ≈ √5, que es el resultado que buscamos |
Lo que resulta, que la exactitud concreta de la Cuadratura del Círculo de Las Meninas es del 98,214285...% usando el Pi de Arquímedes de 22/7.
|
CONSTANTE DE PI |
FRACCIÓN |
RADIO |
ÁREA DEL CÍRCULO | ÁREA DEL CUADRADO |
PRECISIÓN |
||
|
Pi actual |
π | × |
(√5)^2 |
= | 5π = 15,707963... | 4 × 4 |
98,174769...% |
| Zu Chongzhi | 355/113 | × | (√5)^2 | = | 15,707964... | 4 × 4 | 98,174779...% |
|
Velázquez |
1178/375 | × |
(√5)^2 |
= | 15,706666... | 4 × 4 | 98,166666...% |
|
Arquímedes |
22/7 | × |
(√5)^2 |
= | 15,714285... | 4 × 4 |
98,214285...% |
| Alberto Durero | 25/8 | × | (4)^2 | 50 | (√50)^2 = 50 | 100% | |
|
Ahmes |
256/81 | × |
(4,5)^2 |
= | 64 | 8 × 8 |
100% |
|
|
|
|
|
|
Y subrayaríamos que el centro geométrico de la Cuadratura del Círculo de Las Meninas no es un punto cualquiera, sino que su exacta ubicación coincide con el centro de la Sefira nº 6, Tiferet, la Belleza, conocida como el Corazón del Árbol de la Vida, fuente de toda Armonía y Belleza.
Ante estos datos, habría que tener bien presente además la
evolución del valor de la constante Pi; desde su cálculo más remoto, de, al
menos, 36 siglos de antigüedad, hasta su valor numérico exacto actual.
|
CONSTANTE DE PI |
VALOR NUMÉRICO |
FRACCIÓN | DESVIACIÓN |
ORIGEN HISTÓRICO |
|
Pi actual |
3,141592654... |
π | 0 |
Valor actual |
| Zu Chongzhi | 3,141592920... | 355/113 | 0,000000266... | Siglo V |
|
Velázquez |
3,141333333... |
1178/375 | 0,000259321... |
Codificado en Las Meninas |
|
Arquímedes |
3,142857142... |
22/7 | 0,001264489... |
Utilizado en el Siglo XVII |
| Alberto Durero | 3,125 | 25/8 | 0,016592653... | De Symmetria partium - 1532 |
|
Ahmes |
3,160493827... |
256/81 | 0,018901173... |
Papiro de Ahmes |
|
|
Esta tabla confirma que la constante Pi codificada por Velázquez es la clave geométrica y aritmética en Las Meninas, y se acerca al valor actual de Pi con una precisión superior a cualquier otra aproximación racional histórica conocida en España en el siglo XVII.
La fracción 1178/375 se justifica utilizando la pulgada castellana como base de medida.
La definición racional de la constante Pi es el resultado de la relación entre el perímetro y el diámetro de un círculo.
1178 es el valor del perímetro y 375 es del valor del diámetro.
La justificación fundamental es que el numerador de Velázquez, 1178, se descompone exactamente en los módulos geométricos validados en la pulgada castellana de su tiempo:
1178 = 2 × 19 × 31
19 - Corresponde, pues, al tamaño en unidades del lado de un subcuadrado de la rejilla de trabajo de 152 unidades.
31- Es el tamaño histórico del diámetro del círculo en la Geometría de Arquímedes de Pi = 22/7.
Y 375 del denominador corresponde, pues, al resultado de multiplicar el valor de la unidad de 1,125, que equivale a una pulgada, por 333,333333...
El número 375 no es sólo el denominador de la constante π de Velázquez: 1178/375, sino que se revela como la Gematría del nombre de la figura del rey Salomón, la máxima autoridad histórica y mítica en el conocimiento esotérico:
La magia ceremonial,
la construcción de templos
y conocedor de la Geometría Sagrada.
|
|
El código maestro es, por tanto, el número 375, la piedra angular que conecta la ingeniería geométrica de Velázquez con la tradición esotérica de la Kabala, revelando, pues, el propósito ceremonial de Las Meninas.
En otras palabras, Velázquez no sólo resolvía un problema matemático, sino que se puso al servicio de la potestad del rey Salomón, la máxima autoridad en Conocimiento Esotérico y Magia Ceremonial, cuya sabiduría está resumida en 375 aforismos del los Proverbios, desde el 10:1 hasta el 22:16, que, al integrar el número 375 en la fórmula que rige la estructura interior de esta obra maestra, el pintor se investía del poderío necesario para que el acto ceremonial de influir en el destino dinástico tuviera éxito.
Y en consecuencia, se demuestra que Velázquez no sólo construyó su obra con precisión matemática, sino que su objetivo era reflejar el orden cósmico en su lienzo al establecer el centro de la Cuadratura del Círculo en la Sefira nº 6, Tiferet, que simboliza la fuente de toda Armonía.
Una idea que se contrapone a la lúcida experiencia de Dante Alighieri, 1265-1321, que en el Canto XXXIII del Paraíso de la Divina Comedia, daba por imposible la Cuadratura del Círculo:
|
Qual é il geométra che tutto s' affige Per misurar lo cerchio, e non ritrova, Pensando, quel principio ond' egli indige; Tale era lo a quella vista nuova: Veder volea, come si convenne L'imago al cerchio, e come vi s' indova; Ma non eran da ció le proprie penne; Se non che la mia mente fu percossa Da un fulgore, in che sua voglia venne. All´alta fantasia qui mancó possa: Ma giá volgeva il mio disiro e il velle, Si come ruota che igualmente é mossa, L' Amor che muove il Sole e l' altre stelle. |
|
Y como el geómetra que se concentra en medir el círculo, y no encuentra, en su pensamiento el principio que necesita, tal estaba yo con aquella nueva visión. Quería ver cómo la imagen se adaptaba al círculo, y cómo el círculo encajaba allí; pero mis propias fuerzas no estaban para ello salvo que mi mente fue iluminada por un resplandor que dejó satisfecha su deseo. Aquí perdí el sublime vigor de mi fantasía; mas mi anhelo y mi voluntad, ya giraban, como una rueda que se mueve de igual manera que el Amor que anima al Sol y las demás estrellas. |
|
|
El Canto XXXIII del Paraíso es el punto álgido de la culminación de un viaje espiritual, y transmite la metáfora perfecta, de Dante frustrado por el problema irresoluble de la cuadratura del círculo, comparándolo con lo limitado de su mente para comprender la esencia de Dios.
El código maestro de la estructura geométrica y aritmética oculta, que Diego Velázquez utilizó para construir la composición de Las Meninas, transforma este lienzo en un microcosmos que refleja el orden cósmico y la armonía universal, al igual que el Amor, que mueve el Sol y las demás estrellas como apostilló Dante.
Este código se centra en la pretendida solución de la Cuadratura del Círculo, el problema clásico de igualar las área de un círculo y de un cuadrado, que, en el caso del pintor, se resume de la siguiente manera:
Pi de Velázquez: 1178/375 = 3,141333333...
El radio del Círculo de la Cuadratura que mide √5, y que corresponde a 85 unidades.
El centro de la Cuadratura en la coordenada [0, 9], y, además, centro áureo de la rejilla cuadrada de 152 unidades de lado.
Centro que corresponde a la Sefira nº 6, Tiferet, la Belleza, conocida en la Kabala como el Corazón del Árbol de la Vida.
Simbólicamente, la posición exacta del centro de la Cuadratura, coincide con la fuente de toda Armonía.
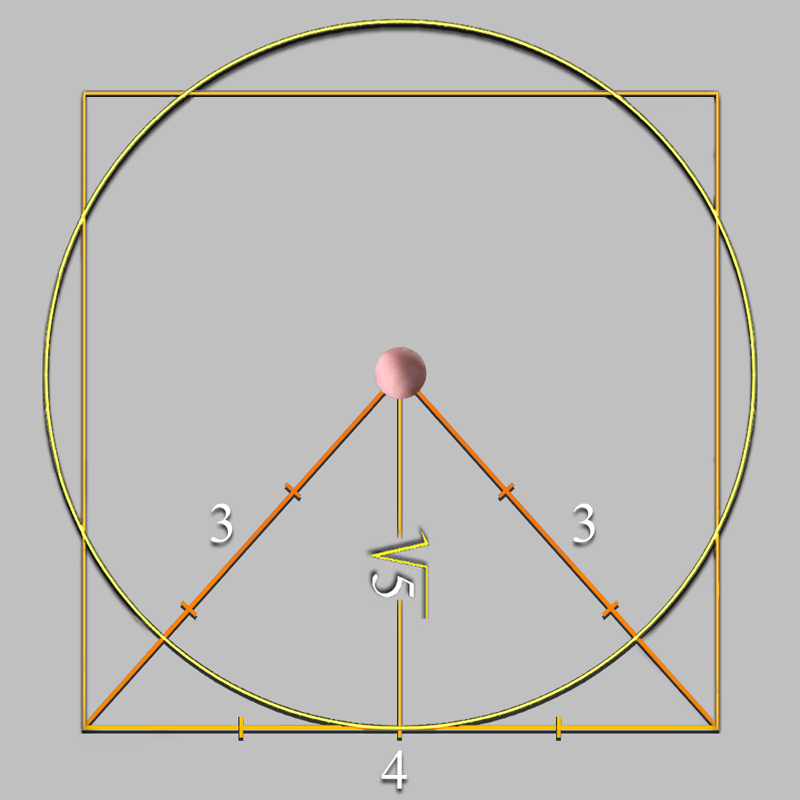 |
|
|
|
CONSTANTE DE PI |
FRACCIÓN |
RADIO |
ÁREA DEL CÍRCULO | ÁREA DEL CUADRADO |
PRECISIÓN |
||
|
Velázquez |
1178/375 | × |
(√5)^2 |
= | 15,706666... | 4 × 4 | 98,166666...% |
|
Área del Cuadrado; 4 × 4 = 16 unidades cuadradas
Área del Círculo; π × (√5)^2 ≈ 15,706666... unidades cuadradas |
El propósito filosófico de Diego Velázquez es negar que la noción de la Cuadratura del Círculo es un problema irresoluble, de manera que el pintor español utiliza la máxima precisión de su época para demostrar que la razón humana, a través del arte, puede codificar y revelar el Orden Cósmico, y la Belleza Divina, y, con esta consideración, esta pintura se convierte en un mapa metafísico donde la Geometría revela la jerarquía y armonía del Árbol de la Vida.
No obstante, cuando hablamos de Cuadrar el Círculo nos referimos, pues, a la sofisticada Geometría del óleo de Las Meninas, que se documenta en el gesto geométrico del pincel, que sujeta Velázquez en su mano derecha, que perfecciona a la obra, y, como marca, hace posible construir el círculo que se relaciona con el cuadrado con una proporción racional; 1178/375 = 3,141333333...,
 |
|
|
Las diferencias históricas, entre las aproximaciones racionales e irracionales de la cuadratura del círculo, eran el centro de la Disputa Geométrica, una disputa cuya esencia se reduce a la pregunta: ¿Qué valor de π es el más idóneo?
Esta Geometría opera con regla y compás, donde solo se pueden construir longitudes que sean números algebraicos, o que se deriven de ellos mediante operaciones aritméticas y raíces cuadradas.
En la página 72 - Dürer, Albrecht. Lutetiae, anno 1532. nonis Augusti, cuyo texto se encontraba en la lista de libros de la Biblioteca de Velázquez, el maestro alemán propone la cuadratura del círculo de la siguiente manera:
|
Operæprecium eſſet ſcire quadraturam circuli, hoc eſt, quadratun conſtituere, propoſito circulo æquale. Sed hoc à philoſophis mathematicen adhuc non demon ſtratun eſt. At in hunc modun id expediri poteſt veriſimiliter, ita quòd in opereparun aut nihil fallat.
Deſcribe quadratum & diuide diametrun eius in decem partes æquales, ex quibus octo ſume pro diametto circuli, velut hic protraxi. |
|
|
|
La tarea consiste en cuadrar un círculo, es decir, construir un cuadrado igual a un círculo dado, pero esto aún no ha sido demostrado por el filósofo matemático, pero de este modo se podría agilizar verdaderamente, y la operación se haría con poco o ningún error.
Diseña un cuadrado y divide su diagonal en diez partes iguales, de las cuales ocho representan el diámetro del círculo, como he dibujado aquí. |
|
PI |
FRACCIÓN | Á. CÍRCULO | Á. CUADRADO | DIFERENCIA | % | |||
|
Actual |
3,141592654... |
π |
50,265482... |
- | 50 | = | 0,265482... | 0,530964...% |
|
Velázquez |
3,141333333... |
1178/375 |
50,261333... |
- | 50 | = | 0,261333... | 0,522666...% |
|
Arquímedes |
3,142857142... |
22/7 |
50,285714... |
- | 50 | = | 0,285714... | 0,571428...% |
| Durero | 3,125 | 25/8 | 50 | - | (√50)^2 = 50 | = | 0 | 0% |
|
|
La propuesta de Alberto Durero no es perfecta, pero sí un elegante ejercicio de Geometría, aunque con un resultado desviado si se le confronta con el Pi de Velázquez, que resulta ser el que menos diferencia genera; a continuación, compararemos los distintos valores de la constante Pi en un círculo de 14 unidades de radio.
La operación fundamental consiste en calcular el Lado del Cuadrado, a partir de la fórmula del área del círculo, que se resuelve en la siguiente expresión matemática:
|
|
|
OPERACIÓN
Resto decimal: 0,8143539...
Resto decimal: 0,861234...
Lado del Cuadrado = 24 partes 48' 52'' |
Los distintos resultados obtenidos del tamaño del Lado del Cuadrado se comparan, pues, con el valor ideal del Pi actual de 24 partes 48' 52'', permitiendo de esta manera evaluar la desviación de cada aproximación histórica.
|
PI |
FRACCIÓN | LADO DEL CUADRADO | DESVIACIÓN |
ORIGEN HISTÓRICO |
|
|
Actual |
3,141592654... |
π | 24 partes 48' 52'' | 0'' |
Valor actual |
| Zu Chongzhi | 3,141592920... | 355/113 | 24 partes 48' 52'' | + 0,3'' | Siglo V |
| Nicolás Cusa | 3,136061224... | 153,667/49 | 24 partes 47' 33'' | - 1' 19'' | Siglo XV |
|
Velázquez |
3,141333333... |
1178/375 | 24 partes 48' 42'' | - 10'' |
1656 en Las Meninas |
|
Arquímedes |
3,142857142... |
22/7 | 24 partes 49' 17'' | + 25'' |
Utilizado en el Siglo XVII |
| Alberto Durero | 3,125 | 25/8 | 24 partes 44' 55' | - 3' 57'' | De Symmetria partium - 1532 |
|
Ahmes |
3,160493827... |
256/81 | 25 partes 1' 44'' | + 2' 52'' |
Papiro de Ahmes |
|
|
A la Teología Católica se la consideraba, pues, la ciencia más alta del conocimiento, y condenaba en El Índice ideas científicas en el mismo momento que Velázquez consolidaba en Las Meninas, adicionalmente, la relación entre La Geometría áurea y El Árbol de la Vida.
El código maestro del pintor resuelve el problema de la Cuadratura del Círculo, tema de debate desde el Renacimiento hasta el siglo XIX, pero revindicando el arte de la Pintura para que rivalizara con la Filosofía y la Teología en la búsqueda de la verdad [23].
|
|
Diego Velázquez, no sólo adelanta a Alberto Durero en exactitud, sino que, en su Geometría, utilizó una base cifrada utilizando 22 letras que equivalen a los ladrillos de los que se sirvió el Arquitecto Divino para la construcción del mundo, un hecho que se aprecia en la Geometría Áurea del Árbol de la Vida, cuya estructura se basa en estas 22 letras.
En Génesis 15:2 existe una alusión implícita al número 318, valor de la Gematría del nombre Eliezer, mayordomo de Abraham, de modo que este guarismo sugiere que, si se utilizara 3,18 como aproximación del número Pi, entonces, a una circunferencia con ese perímetro le correspondería exactamente un diámetro de 1 unidad [24].
| ר | ז | ע | י | ל | א | |||||||
| 200 | + | 7 | + | 70 | + | 10 | + | 30 | + | 1 | = | 318 |
|
|
Y viniendo al paso, la palabra hebrea Elohim, אֱלֹהִים, es la más utilizada en el Antiguo Testamento para mencionar a Dios, y es un nombre en plural que significa Dioses o Los Poderosos, y que, además, se emplea para referirse al Dios de Israel como el Creador supremo, enfatizando su poder y majestad.
Y, en consecuencia, si analizamos la Gematría de las cinco letras de la palabra ELOHIM en un Cuadrado Mágico de 5 x 5 casillas.
Tendremos:
|
M |
I |
H |
L |
E |
|
ם |
י |
ה |
ל |
א |
|
4 |
1 |
5 |
3 |
1 |
 |
Y, observaremos, pues, en la primera línea superior de este Cuadrado Mágico, el valor del número Pi,
y la serie completa de los tres números pitagóricos por excelencia:
|
3 |
+ |
1 |
+ |
4 |
+ |
1 |
+ |
5 |
= |
14 |
Hablamos, pues, de la conexión de la palabra ELOHIM con el número Pi con una exactitud impresionante.
La palabra, היםאל, Ha-yam El, leída como una sola palabra tiene una lectura basada en la combinación de dos términos existentes:
הים - Ha-yam: el mar.
אל - El: Dios o poderoso.
De modo, que la combinación היםאל se traduciría literalmente como El mar de Dios, y reforzaría la idea de que la Causa Primera, Elohim, es el poder ordenador que domina las fuerzas del caos, un concepto central en muchos mitos de la creación del Antiguo Oriente Próximo.
Velázquez, pues, no sólo encubrió un código geométrico, sino que reveló la constante clave que rige el Cosmos, que es, en definitiva, lo que la Teología de la época consideraba lo más alto del conocimiento.
Esta lectura nos dirige a la división en círculos de las Esferas, que propuso su autor Claudio Ptolomeo, con un Pi perfecto, como así lo tiene la Causa Primera: ELOHIM, lo que sugiere que no solo creó el mundo, sino que, como Gran Geómetra, lo hizo bajo la proporción perfecta de la circunferencia, la forma geométrica que representa la eternidad y la unidad.
Este argumento simbólico sintetiza la perfección geométrica de los círculos ptolemaicos y la naturaleza intrínseca del número Pi relacionados con la Causa Primera, ordenada y matemáticamente precisa, identificada con ELOHIM.
Es decir; una interpretación filosófica que encuentra armonía divina tanto en las estructuras cosmológicas antiguas como en las constantes matemáticas universales actuales.
|
|
Figura de la diuiſion de las Spheras
Libro de la COSMOGRAPHIA - Pedro Apiano - MDXLVIII - Enveres |
En la esfera más alta, se situaba el Decimum Cœlum, que Aristóteles en su Metafísica la denominó EL PRIMER MÓVI o la Causa Primera, que, en su desplazamiento diario, movía a todas las estrellas fijas, y a los siete planetas que orbitaban alrededor de la Tierra, y, en lo más elevado, el Empíreo circundaba a los diez círculos celestes.
CIELO EMPÍREO LA HABITACIÓN DE DIOS Y TODOS LOS ELEGIDOS
notas a pie de página
1 - Página 37 - Luca Pacioli - La Divina proporción - Ediciones Akal, S. A. - 1991. Del manuscrito existente en la Biblioteca Ambrosiana de Milán dedicado al Duque de Milán Ludovico il Moro. Traducción de Juan Calatrava.
2 - En el diccionario: Tesoro de la Lengua Castellana:
|
|
Publicado en Madrid en el año 1611 encontramos la palabra KABALA definida en estos términos:
|
CABALA, es cierta dotrina miſtica entre los Iudios: la qual no ſe eſcriue, ſino que de vno en otro, ſe va conſeruando, tomandola de cabeça, y los que la profeſſan, ſe llaman Cabaliſticos, de la dicha raiz קָבַל in piel קָבַל ſuſcipere, recipere, &c. |
|
|
A partir de su origen judaico, la difusión de la Kabala varía de acuerdo a la tradición y los objetivos que persigue, ya que, como herramienta mística, existe una adaptación posterior cristiana y otra ocultista.
3 - Página 122. Theatro Critico Universal. Benito Jerónimo Feijóo. Madrid. M.DCC.LXXIII.
4 - A finales del reinado de Felipe II, Juan de Herrera, el arquitecto del Escorial, será el promotor y primer director de la Academia Real Matemática; comenzando su andadura en dependencias de Palacio en Octubre de 1583.
Desde 1612, la Academia ejercerá su labor didáctica en casa del Marqués de Leganés, hasta que es clausurada en 1630; fechas en las que aún Diego Velázquez tuvo ocasión de estudiar y practicar sus instrumentos antes de viajar por primera vez a Italia.
Don Diego de Messía, Marqués de Leganés, primo carnal del Conde Duque de Olivares, fue tanto el promotor de la conquista por lo exacto, como experto coleccionista de pintura.
Según se deduce del inventario de su Segundo mayorazgo, y de acorde a Mary Crawford Volk, en 1642 había en esta colección, al menos, cinco obras de Velázquez:
El retrato de la Reina de Hungría, hoy en el Museo del Prado,
uno de Calabazas con turbante,
otro de Pablillos,
un autorretrato del propio pintor
y un San Francisco de Paula con dos compañeros.
Paralelamente, en 1581 María de Austria, hija de Carlos V, al morir su esposo, el emperador Maximiliano, se retiraba a Madrid; y generosa benefactora de los jesuitas en Alemania, lo continuó siendo en la capital de España.
A la muerte de María el pequeño colegio, que la Compañía de Jesús había fundado en 1572, se le denominará Colegio Imperial.
En 1624, tras el fallecimiento de Juan Bautista Labaña, el último que quedaba de la fundación de la academia de Madrid, y que había sido profesor de matemáticas de un entonces joven príncipe Felipe, por real decreto, en el Colegio se crearán veintitrés cátedras en Enero de 1625.
Las materias que impartiría el Colegio incluirían las lenguas clásicas, la historia, la filosofía natural, las matemáticas, las artes militares, políticas y económicas; para, así mismo, interpretar las de Aristóteles, ajustando la razón de estado con la conciencia, religión y fe católica.
El rey se constituía como fundador y patrón de los Estudios Reales, función que había de pasar a sus sucesores.
A la postre, el Colegio Imperial, en Febrero de 1629, se haría cargo de la enseñanza de las Matemáticas en la Corte.
al cálculo mercantil,
a la fundamentación de la cosmografía,
a la astrología,
al arte de navegar,
al arte militar
y a la técnica de la construcción.
Sin embargo, era heroico el de algunos practicarla a principios del siglo XVII en el Reino de las Españas, ya que, tal y como afirma el valenciano Miguel Geronimo de Santa Cruz; quien contar no supiese no se le tenía como hombre.
Página 54. LIBRO DE ARITHMETICA ESPECULATIVA Y PRACTICA. EL DORADO CONTADOR de Miguel Geronimo de Santa Cruz. Impreso en Sevilla. 1601.
Dentro de este Código recopilado por las Cortes de Valladolid y Madrid a partir de 1523; de las Leyes del Fuero Real, las 18 Leyes de Toro, el Ordenamiento de Alcántara y el de Montalvo, se enmarca la pragmática dictada por el propio monarca desde El Escorial el 24 de junio de 1568:
|
Y otroſi, que el paño y lienço y ſayal, y las otras coſas que ſe venden a varas, que ſe vendan por la vara Caſtellana: y en cada vara, que den una pulgada al traues, y que se midan el paño por eſquina: y declaramos que la vara Caſtellana de que ſe ha de vſar en todos eſtos Reynos, ſea la que hay y tiene la ciudad de Burgos. |
Libro quinto - Titulo XIII. RECOPILACION de las Leyes deſtos Reynos, hecha por mandado de la Mageſtad Catholica del Rey don Philippe Segundo nuestro Señor. Alcala de Henares, en casa de Iuan Iñiguez de Liquerica impreſſor de libros. Año M.D.LXXXI.
7 - Página 6 - Tratado general de monedas, pesos, medidas y cambios de todas las naciones, reducidas a las que se usan en España.Tomás Antonio de Marien y Arróspide, Madrid. 1789.
8 - Uno de los libros más antiguos que hemos estudiado sobre; Aritmética, Álgebra, Trigonometría y otros cálculos, es del año 1688, editado por el Colegio de la Compañía de Jesús de la ciudad de Cádiz.
En este libro se pone a prueba, didácticamente, la eficacia de los números; en los quebrados, en las proporciones..., y su aplicación práctica final trasladada a la Arquitectura Militar.
THESES MATHEMATICAS - Defendidas por: El Exmo. Señor Don Iñigo de la Cruz Manrique de Lara Remirez de Arellano Mendoza y Alvarado, Conde de Aguilar, Señor de los Cameros, Marqués de la Hinojoſa, Conde de Uillamor, Señor del Eſtado de Andaluz, y Mayalde, y de la Caſa de Carrillo en el Reyno de Nauarra, &c. - Cadiz - Año 1688 - XXII de Junio.
9 - La opinión del maestro de Velázquez, Francisco Pacheco, nos parece el mejor ejemplo, y explica:
|
El modo de ver ſe haze mediante la luz, en forma de Piramide, formada de los rayos viſuales que proceden de la viſta, donde es la punta de la piramide, i por eſtos rayos los ſimulacros e imagines de las coſas viſibles ſe imprimen en la potencia viſiva. La coſa viſta cuya imagen ſe repreſenta, viene a ſer la baſa deſta piramide, i aſsi forçoſſamente a de ſer de cantidad ſenſible, reſpeto de la ſuperficie del ver. La diſtancia entre la viſta, i lo que ſe vè a de ſer proporcionada, i conveniente, porque ſiendo mui remota, o mui propincua, las coſas viſibles no pueden ſer comprehendidas de la viſta, ni repreſentadas en la pintura. I aſsi la diſtancia a de correſponder a la viſta, con cierta razon i proporción de Angulos; porque la grandeza de las coſas que vemos tanto parece mayor, o menor, cuanto de mayor, o menor angulo viene a ſer comprehendida de la viſta. I eſta grandeza de los angulos viſuales se altera mudandose la diſtancia, i ſe viene a variar el aſpecto. I por eſta cauſa ſe a de tener entera noticia de la figura i cantidad que tienen los cuerpos en ſu propia forma, para ſaber los que diminuyen, i ſe acortan a la viſta, por la diſtancia, i variedad de los angulos. |
|
|
La pirámide visual de las distintas proporciones de la pared del fondo de Las Meninas parte del punto de fuga, pero su trazado está basado en el Primer Teorema de Thales de Mileto.
Thales vivió hacia el año 600 a. c., y, por ser el más antiguo de los Siete Sabios de Grecia, habría que considerarle el abuelo de la Geometría.
Como definición previa al enunciado del teorema, es necesario determinar que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí.
Primer teorema:
Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes. |
Primera Tabla
Formatos en base al tamaño de la anchura de 72 unidades de la pared del fondo:
|
formato |
proporción |
|
escala |
|
unidades |
|
pulgadas |
metros |
|
La anchura de la Habitación del Príncipe mide 5,58 metros |
||||||||
|
30 |
30/9 |
= |
3,333.333 |
x |
72 |
= |
240 |
30 x 8 x 0,02325 = 5,58 |
|
29 |
29/9 |
= |
3,222.222 |
x |
72 |
= |
232 |
29 x 8 x 0,02325 = 5,394 |
|
28 |
28/9 |
= |
3,111.111 |
x |
72 |
= |
224 |
28 x 8 x 0,02325 = 5,208 |
|
27 |
27/9 |
= |
2,999.999 |
x |
72 |
= |
216 |
27 x 8 x 0,02325 = 5,022 |
|
26 |
26/9 |
= |
2,888.888 |
x |
72 |
= |
208 |
26 x 8 x 0,02325 = 4,836 |
|
25 |
25/9 |
= |
2,777.777 |
x |
72 |
= |
200 |
25 x 8 x 0,02325 = 4,65 |
|
24 |
24/9 |
= |
2,666.666 |
x |
72 |
= |
192 |
24 x 8 x 0,02325 = 4,464 |
|
23 |
23/9 |
= |
2,555.555 |
x |
72 |
= |
184 |
23 x 8 x 0,02325 = 4,278 |
|
22 |
22/9 |
= |
2,444.444 |
x |
72 |
= |
176 |
22 x 8 x 0,02325 = 4,092 |
|
21 |
21/9 |
= |
2,333.333 |
x |
72 |
= |
168 |
21 x 8 x 0,02325 = 3,906 |
|
20 |
20/9 |
= |
2,222.222 |
x |
72 |
= |
160 |
20 x 8 x 0,02325 = 3,72 |
|
19 |
19/9 |
= |
2,111.111 |
x |
72 |
= |
152 |
19 x 8 x 0,02325 = 3,534 |
|
18 |
18/9 |
= |
1,999.999 |
x |
72 |
= |
144 |
18 x 8 x 0,02325 = 3,348 |
|
17 |
17/9 |
= |
1,888.888 |
x |
72 |
= |
136 |
17 x 8 x 0,02325 = 3,162 |
|
16 |
16/9 |
= |
1,777.777 |
x |
72 |
= |
128 |
16 x 8 x 0,02325 = 2,976 |
|
15 |
15/9 |
= |
1,666.666 |
x |
72 |
= |
120 |
15 x 8 x 0,02325 = 2,79 |
|
14 |
14/9 |
= |
1,555.555 |
x |
72 |
= |
112 |
14 x 8 x 0,02325 = 2,604 |
|
13 |
13/9 |
= |
1,444.444 |
x |
72 |
= |
104 |
13 x 8 x 0,02325 = 2,418 |
|
12 |
12/9 |
= |
1,333.333 |
x |
72 |
= |
96 |
12 x 8 x 0,02325 = 2,232 |
|
11 |
11/9 |
= |
1,222.222 |
x |
72 |
= |
88 |
11 x 8 x 0,02325 = 2,046 |
|
10 |
10/9 |
= |
1,111.111 |
x |
72 |
= |
80 |
10 x 8 x 0,02325 = 1,86 |
|
9 |
9/9 |
= |
0,999.999 |
x |
72 |
= |
72 |
9 x 8 x 0,02325 = 1,674 |
|
La anchura de la pared del fondo pintada en el lienzo de Las Meninas mide 1,488 metros |
||||||||
|
8 |
8/9 |
= |
0,888.888 |
x |
72 |
= |
64 |
8 x 8 x 0,02325 = 1,488 |
|
7 |
7/9 |
= |
0,777.777 |
x |
72 |
= |
56 |
7 x 8 x 0,02325 = 1,302 |
|
6 |
6/9 |
= |
0,666.666 |
x |
72 |
= |
48 |
6 x 8 x 0,02325 = 1,116 |
|
5 |
5/9 |
= |
0,555.555 |
x |
72 |
= |
40 |
5 x 8 x 0,02325 = 0,93 |
|
4 |
4/9 |
= |
0,444.444 |
x |
72 |
= |
32 |
4 x 8 x 0,02325 = 0,744 |
|
3 |
3/9 |
= |
0,333.333 |
x |
72 |
= |
24 |
3 x 8 x 0,02325 = 0,558 |
|
2 |
2/9 |
= |
0,222.222 |
x |
72 |
= |
16 |
2 x 8 x 0,02325 = 0,372 |
|
1 |
1/9 |
= |
0,111.111 |
x |
72 |
= |
8 |
1 x 8 x 0,02325 = 0,186 |
|
0 |
0/9 |
= |
0,000.000 |
x |
72 |
= |
0 |
0 x 8 x 0,02325 = 0 |
|
|
|
|
|
|
Segunda Tabla
Formatos en base al tamaño de la altura de 59,4 unidades de la pared del fondo:
|
formato |
proporción |
|
escala |
|
unidades |
|
pulgadas |
metros |
|
La altura de la Habitación del Príncipe mide 4,65 metros |
||||||||
|
30 |
30/9 |
= |
3,333.333 |
x |
60 |
= |
200 |
30 x 6,666 x 0,02325 = 4,65 |
|
29 |
29/9 |
= |
3,222.222 |
x |
60 |
= |
193 y 1/3 |
29 x 6,666 x 0,02325 = 4,495 |
|
28 |
28/9 |
= |
3,111.111 |
x |
60 |
= |
186 y 2/3 |
28 x 6,666 x 0,02325 = 4,34 |
|
27 |
27/9 |
= |
2,999.999 |
x |
60 |
= |
180 |
27 x 6,666 x 0,02325 = 4,185 |
|
26 |
26/9 |
= |
2,888.888 |
x |
60 |
= |
173 y 1/3 |
26 x 6,666 x 0,02325 = 4,03 |
|
25 |
25/9 |
= |
2,777.777 |
x |
60 |
= |
166 y 2/3 |
25 x 6,666 x 0,02325 = 3,875 |
|
24 |
24/9 |
= |
2,666.666 |
x |
60 |
= |
160 |
24 x 6,666 x 0,02325 = 3,72 |
|
23 |
23/9 |
= |
2,555.555 |
x |
60 |
= |
153 y 1/3 |
23 x 6,666 x 0,02325 = 3,565 |
|
22 |
22/9 |
= |
2,444.444 |
x |
60 |
= |
146 y 2/3 |
22 x 6,666 x 0,02325 = 3,41 |
|
21 |
21/9 |
= |
2,333.333 |
x |
60 |
= |
140 |
21 x 6,666 x 0,02325 = 3,255 |
|
20 |
20/9 |
= |
2,222.222 |
x |
60 |
= |
133 y 1/3 |
20 x 6,666 x 0,02325 = 3,1 |
|
19 |
19/9 |
= |
2,111.111 |
x |
60 |
= |
126 y 2/3 |
19 x 6,666 x 0,02325 = 2,945 |
|
18 |
18/9 |
= |
1,999.999 |
x |
60 |
= |
120 |
18 x 6,666 x 0,02325 = 2,79 |
|
17 |
17/9 |
= |
1,888.888 |
x |
60 |
= |
113 y 1/3 |
17 x 6,666 x 0,02325 = 2,635 |
|
16 |
16/9 |
= |
1,777.777 |
x |
60 |
= |
106 y 2/3 |
16 x 6,666 x 0,02325 = 2,48 |
|
15 |
15/9 |
= |
1,666.666 |
x |
60 |
= |
100 |
15 x 6,666 x 0,02325 = 2,325 |
|
14 |
14/9 |
= |
1,555.555 |
x |
60 |
= |
93 y 1/3 |
14 x 6,666 x 0,02325 = 2,17 |
|
13 |
13/9 |
= |
1,444.444 |
x |
60 |
= |
86 y 2/3 |
13 x 6,666 x 0,02325 = 2,015 |
|
12 |
12/9 |
= |
1,333.333 |
x |
60 |
= |
80 |
12 x 6,666 x 0,02325 = 1,86 |
|
11 |
11/9 |
= |
1,222.222 |
x |
60 |
= |
73 y 1/3 |
11 x 6,666 x 0,02325 = 1,705 |
|
10 |
10/9 |
= |
1,111.111 |
x |
60 |
= |
66 y 2/3 |
10 x 6,666 x 0,02325 = 1,55 |
|
9 |
9/9 |
= |
0,999.999 |
x |
60 |
= |
60 |
9 x 6,666 x 0,02325 = 1,395 |
|
La altura de la pared del fondo pintada en el lienzo de Las Meninas mide 1,24 metros |
||||||||
|
8 |
8/9 |
= |
0,888.888 |
x |
60 |
= |
53 y 1/3 |
8 x 6,666 x 0,02325 = 1,24 |
|
7 |
7/9 |
= |
0,777.777 |
x |
60 |
= |
46 y 2/3 |
7 x 6,666 x 0,02325 = 1,085 |
|
6 |
6/9 |
= |
0,666.666 |
x |
60 |
= |
40 |
6 x 6,666 x 0,02325 = 0,93 |
|
5 |
5/9 |
= |
0,555.555 |
x |
60 |
= |
33 y 1/3 |
5 x 6,666 x 0,02325 = 0,775 |
|
4 |
4/9 |
= |
0,444.444 |
x |
60 |
= |
26 y 2/3 |
4 x 6,666 x 0,02325 = 0,62 |
|
3 |
3/9 |
= |
0,333.333 |
x |
60 |
= |
20 |
3 x 6,666 x 0,02325 = 0,465 |
|
2 |
2/9 |
= |
0,222.222 |
x |
60 |
= |
13 y 1/3 |
2 x 6,666 x 0,02325 = 0,31 |
|
1 |
1/9 |
= |
0,111.111 |
x |
60 |
= |
6 y 2/3 |
1 x 6,666 x 0,02325 = 0,155 |
|
0 |
0/9 |
= |
0,000.000 |
x |
60 |
= |
0 |
0 x 6,666 x 0,02325 = 0 |
Tabla del formato de la altura de la pared
del fondo
10 - La Cábala, La tradición de los conocimientos oscuros. Z´ev Ben Shimon Halevi. DEBATE ediciones del Prado, 1994.
Publicado de acuerdo con Thames and Hudson Ltd., Londres. Título original: Kabbalah. Editor general de la serie, Jill Purce. Warren Kenton, 1979.
11 - LA OPERAZIONE DEL COMPASSO GEOMETRICO ET MILITARE DI GALILEO GALILEI. PADOVA, M.DC.XL.
12 - IL COMPASSO. Con Altri Istromenti Mathematici. Fabritio Mordente. Anversa. M. D. LXXXIIII.
13 - Página 304 - Velázquez. Homenaje en el centenario de su muerte. Instituto Diego Velázquez. Consejo Superior de Investigaciones Científicas. Madrid, 1960.
14 - Página 349 - I DIECI LIBRI DELL´ARCHITETTURA DI M. VITRVVIO. Tradotti & commentati da Monſ. Daniel Barbaro eletto Patriarca d´Aquileia, da lui riueduti & amplati; & hora in piu commoda forma ridotti. In Venetia, MDLXVII.
Libro IX – Cap. II.
Della ſquadra inuentione di Pitagora per formare l´angulo giusto.
|
Pitagora ſimilmente dimoſtrò la ſquadra ritrouata ſenza opera di artefice alcuno, & fece chiato con quanto grande fatica i fabri facendola, a pena la poſſono al giuſto ridurre. Queſta coſta con ragioni, & uie emendata, da ſuoi precetti ſi manifeſta: perque ſe egli ſi prenderà tre regole, una di piedi tre, l´altra di quattro, la terza di cinque, & queſte regole compoſte ſiano, che con i capi ſi tocchino inſieme facendo una figura triangulare, condurranno la ſquadra giuſta. |
15 - Página 95 - Tratado de Geometria Practica y Speculatiua. Iuan Perez de Moya. Alcala. M. D. LXX. III.
Escribe el español Iuan Perez de Moya:
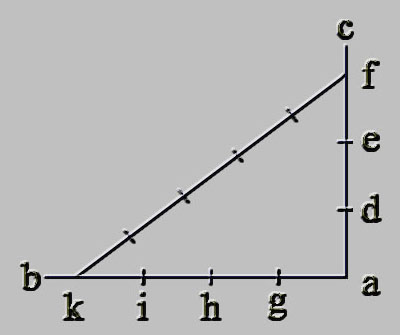
Luego toma en el otro lado, ò linea a. b. quatro
tamaños ſemejantes à eſtos como denota g. h. i. k. Saca agora
vna linea recta deſde el punto f. haſta el punto k. y ſi eſta
linea tuuiere cinco tamaños ſemejantes a los tres que tomaſte en
el lado a. c. ò a los quatro del lado a. b. la tal eſquadra ſera
verdadera, y ſi ay menos, o mas tamaños de cinco eſtara falſa,
como ſe prueua por la penultima del primero de Euclides. Porque
ſi el angulo a. es recto, el quadrado de la linea a. f. y a. k.
ha de ſer ygual al quadrado de la linea f. k. que es lado opueſto
al dicho angulo recto, pues ſi el lado a. f. tiene tres tamaños,
y en el a. k. tiene quatro, la ſumma de los quadrados deſtos
numeros 3. y 4. es 25. Luego el otro lado f. k. es neceſſario
que tenga cinco tamaños, para que ſu quadrado haga veynte y
cinco, que es lo que haze la ſumma de los quadrados de los otros
lados que comprehenden el angulo recto. Ha ſe dicho eſto aquí
porque como con eſte inſtrumento ſe ha de moſtrar medir
diſtancias, es bien ſaberle hazer.
|
16 - Libro I - Theorema. 2. - Propoſition. 5.
|
|
|
|
DEMOSTRACIÓN
LOS SEIS LIBROS PRIMEROS DE LA GEOMETRIA DE EVCLIDES - Rodrigo Çamorano. Seuilla. 1576.
17 - La escala es la relación proporcional entre la dimensión real de un objeto y las de este mismo objeto representado sobre un plano.
|
Siempre que el Arquiteto quiere hazer vna traça, lo primero que haze antes que la comience, es hazer el pitipie: y porque aura muchos, que no ſepan que cosa es pitipie, pongo aqui ſu declaracion. El pitipie es nombre Frances, que peti en Frances quiere dezir pequeño, ò chico, y aſsi es lo meſmo dezir en nuestra lengua Caſtellana pequeño pie, como en Frances pitipie, y por eſto ſe entendera, que eſte pequeño pie es ſemejança del pie grande, aduirtiendo que tres pies de los grandes, ſon una vara Caſtellana, y quando ſe mide las fabricas ſe entiende yr medidas debaxo de que tres pies hazen la dicha vara, y con eſta proporcion ſe hace el pitipie, el qual ſirve para hazer las traças y modelos, y va hecho con proporcion del tamaño que ha de tener la fabrica grande, porque aunque ſea la traça no mayor que vn real de à ocho, como vaya repartida con ſu pitipie, ſe entendera por ella la grandeza que ha de tener, pueſta en execucion: porque ſe conſideran aquellas pequeñas medidas reſpeto de las grandes hechas con el gran pie, y aſsi meſmo à este pitipie le llaman muchos eſcala. |
|
|
|
En el circulo, el angulo que eſta en el medio circulo es recto, y el que eſta en el ſegmento mayor, es menor que recto, y el que en el menor ſegmento, es mayor que recto. Y de mas de eſto el angulo del mayor ſegmento es mayor que recto; y el angulo del menor ſegmento es menor que recto. |
19 - Libro I - Theorema. 33. - Propoſitio. 47.
|
En los triangulos rectangulos el quadrado que es hecho de el lado que eſta opueſto al angulo recto es ygual a los dos quadrados que ſon hechos de los lados que contienen el angulo recto. |
|
|
|
Sea el triangulo rectangulo .ABC. que tenga recto el angulo BAC. digo que el quadrado que es hecho del lado .EC. es ygual a los quadrados que ſe hazen de .BA. y de .AC. Deſcribaſe, por la .46. de la .BC. el quadrado .BDCE, y por la miſma, de la BA. y de la, AC. los quadrados .ABZI. ACKT. y por el punto A. tireſe .AL. parallela con la .BD. CE, por la propoſicion .31, y por la .I. peticion tireſe AD. CZ. y porque los angulos. BAC. BAI. ſon rectos. Luego tiradas dos lineas rectas .AC. AI. deſde vna linea recta .AB. y deſde vn punto en ella .A. no hacia vnas miſmas partes hacen de vna y otra parte angulos yguales a dos rectos por la .14. propoſition, luego en derecho eſta la .AC. de la .AI y por eſto tambien BA eſta en derecho de .AT y porque el angulo .DBC. es ygual al angulo .ZBA. porque cada vno dellos es recto; pongaſe comun el angulo ABC. Luego todo DBA es ygual a todo el angulo ZBC. y porque las dos .AB. BD. ſon yguales a las dos BZ. BC. la vna a la otra, y el angulo .DBA es ygual al angulo .ZBC. luego la baſis .AD, por la .4. propoſicion, es ygual a la baſis .ZC. y el triangulo .ABD. al triangulo .ZBC. es tambien igual. Y el parallelogramo .BL, por la 41, es doblo del triangulo .ABD. porque tiene vna miſma baſis que es .BD. y esta en vnas miſmas parallelas, es a ſaber .DB. AL. y tambien el quadrado .IB. por la miſma, es doblo del triangulo .ZBC. porque tiene la miſma baſis que es .BZ. y eſta en vnas miſmas parallelas, es a ſaber .ZB. IC. y las coſas que ſon doblo de coſas yguales, por la .6. comun ſentencia, entre ſi ſon yguales. Luego el parallelogramo .BL. es ygual al quadrado .IB Semejantemente ſi por .I. peticion, ſe tiran .AE BK. ſe demoſtrara el parallelogramo CL. ſer ygual al quadrado .TC. Luego todo el quadrado .BDEC, es ygual a los dos quadrados .IB, TC. Y el quadrado .BDEC. es hecho de la .BC. y los quadrados IB. CT. ſon hechos de la .BA. AC. Luego el quadrado que de el lado .BC. ſe hizo es ygual a los quadrados que ſon hechos de los lados .BA. AC. luego en los triangulos rectangulos el quadrado que es hecho del lado que eſta oppueſto al angulo recto y lo que mas ſe ſigue como en el theorema, que ſe hauia de demoſtrar. |
DEMOSTRACIÓN
LOS SEIS LIBROS PRIMEROS DE LA GEOMETRIA DE EVCLIDES - Traduzidos en lengua Eſpañola por Rodrigo Çamorano Aſtrologo y Mathematico, y Cathedratico de Coſmografia por ſu Mageſtad en la caſa de la Contratacion de Seuilla. Dirigidos al illuſtre ſeñor Luciano de Negron, Canonigo de la ſancta ygleſia de Seuilla. Con licencia del Conſejo Real. En Seuilla en caſa de Alonſo de la Barrera. 1576.
21 - Página 170 - Metrification for Manufacturing. E. R. FRIEST, P. E. New York. 1978.
Estándares Básicos: Pulgada y Métrico
|
22 - Página 199 - 6.6 CONSTRUCCIÓN DE ROSCAS CUANDO NO SE DISPONE DE LA RUEDA DE 127 DIENTES
Cuando no tenemos la rueda de 127 dientes, podemos realizar roscas inglesas en torno métrico y roscas métricas en torno inglés sustituyendo el valor de la pulgada (25,4) por su aproximado 1600/63.
1600/63 es igual a 25,3968 y como 25,4 - 25,3968 es igual a 0,0032 tenemos un error despreciable en casi todos los casos.
TECNOLOGÍA MECÁNICA, Raúl García Bercedo, Iñaki Irastorza Hernando, Amaia Castaños Urkullu, Esperanza Díaz Tajada. Servicio Editorial de la Universidad del País Vasco. Euskal Herriko Unibertsitateko Argitalpen Zerbitzua. 2013.
23 - THE POLEMIC PROBLEM: What is the value of Pi. Gould, S. C. (Sylvester Clark). Publisher Manchester, N.H. 1888.
24 - El texto de Génesis 14:14 está relacionado con el pasaje de Génesis 15:2, que indica que Abraham armó a 318 criados para rescatar a Lot. El Midrash y comentaristas como Rashi sugieren que este número se refiere específicamente a Eliezer, cuyo nombre equivale a 318, implicando que él solo valía por todo un ejército.
|
La Kabala y Las Meninas |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |