|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fantoni tiene licencia CC BY-NC 4.0 |
|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fantoni tiene licencia CC BY-NC 4.0 |
|
|
En 1525 el maestro Alberto Durero
publica una obra titulada:
Instrucción sobre la medida con regla y compás de figuras planas y sólidas ...
|
Vnderweyſung der meſſung / mit dem zirckel vnd richt ſcheyt / in Linien ebnen vnnd ganßen corporen / durch Albrecht Dürer zü ſamen geßogen / vnd zü nuß allen kunſtlieb habenden mit zü gehörigen figuren / in truck gebracht / im jar. M. D. X X v. |
Este libro pretendía mostrar a los artistas, pintores y matemáticos de la época, diversos métodos para trazar, con regla y compás, figuras geométricas, y, entre ellas, destacamos la siguiente espiral.
|
|
|
|
Aunque también habría que subrayar que esta espiral de Alberto Durero estuvo precedida por la espiral basada en la sección áurea de la sucesión; 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144..., de Fibonacci [1].
|
|
|
|
Con la ayuda de la Sucesión de Fibonacci se construye, pues, una espiral gnómica basada en el famoso número de oro, o mejor dicho, en rectángulos áureos, que son aquellos cuyos lados están en proporción áurea, es decir; el cociente entre su lado mayor y su lado menor se aproxima al valor del número de oro [2].
La proporción áurea de estos rectángulos viene determinada por el cociente entre las medidas de sus lados:
1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ...
|
Sucesión de Fibonacci |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
|
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
|
Aproximación a Phi |
1 |
2 |
1,5 |
1,6666 |
1,6 |
1,625 |
1,6153 |
1,6190 |
1,6176 |
1,6181 |
1,6179 |
A medida que los lados de estos rectángulos crecen, al mismo tiempo, la relación de sus lados se va acercando al rectángulo áureo, por lo que esta sucesión de cocientes tiende a estabilizarse en un número próximo a 1,618..., es decir; el valor del número áureo:
|
|
|
El número áureo Phi |
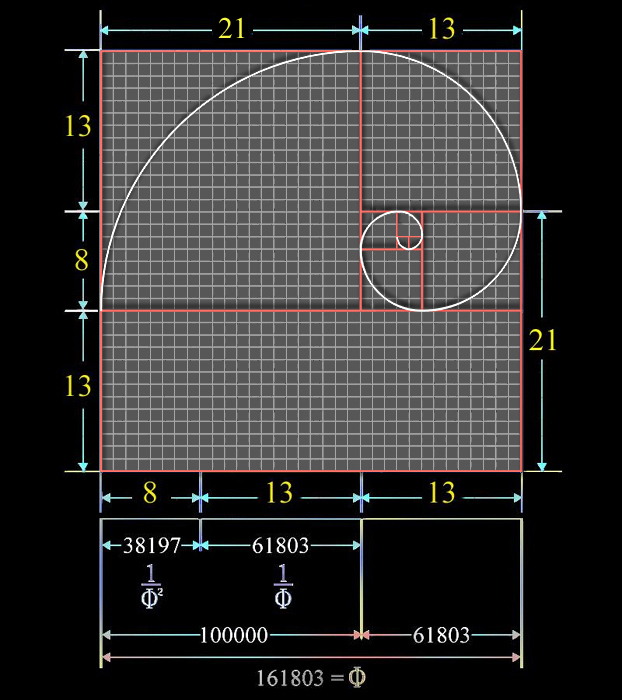
Para generar el dibujo de esta curva partimos de dos pequeños cuadraditos de lado igual a una unidad [3], es decir, de 8/9 de pulgada de lado, que constituyen, pues, un primer rectángulo cuyo lado mayor es 2, y el menor, como se puede entender, vale 1.
LA CUADRÍCULA DE LA ESPIRAL
 |
|
|
La espiral crece en paralelo a la instalación de un nuevo cuadrado de 2 x 2, el cual lo dibujamos junto al rectángulo anterior, y de este modo obtenemos un nuevo rectángulo de 3 x 2.
A partir de aquí el proceso se repite añadiéndose más cuadrados, cuyos lados miden, en unidades, las mismas cifras que los números de la sucesión de Fibonacci; que son, en definitiva, la estructura base de la construcción de tan enroscada órbita.
|
|
|
|
La Espiral de Las Meninas nace en el centro del pecho de la Infanta Margarita de Austria, es decir; en su propio esternón.
Y al mismo tiempo, el tiento que sujeta el pintor en su mano izquierda apunta hacia la entrada de un mundo espiritual, en el techo de la Habitación del Príncipe, con el fin de reconocer lo invisible, mientras que el pincel dirigido hacia el suelo, en respuesta, recuerda que se nace de la tierra, y que, después de la liberación del alma, el cuerpo retornará a ella.
|
|
|
|
Con esta reivindicación admitimos, pues, que el pintor interioriza su experiencia mística, y se aferra a Dios en estado de devekut, דבקות.
La coordenada del punto Q -0,5 : [- 36, - 0,5], se acomoda a media altura de la arista lateral izquierda de la pared del fondo, que se halla totalmente oculta tras el larguero de madera del Gran Bastidor en el primer plano.
La distancia geométrica y física entre el punto Q -0,5 y el punto S : [0, - 63] es igual a la que hay entre el punto Q -0,5 y el punto R.
|
Q -0,5 S = Q -0,5 R |
El trazado del tiento de madera discurre desde el punto T : [- 34, - 76] hasta la coordenada del punto R : [0, 62], en el centro de la Sefira nº 1 Kether, La Corona.
|
|
|
|
En el trazado de este vector, pues, hacemos una parada de rigor en el punto W : [- 17, - 7] , y observamos, que esta coordenada, W, se encuentra situada, exactamente, en el punto medio de su ascenso, y justo debajo de la vertical del enganche de la Lámpara Kether.
|
TW = WR |
Geométricamente, esta certera vertical y la horizontal a la altura de la nuez de la garganta del pintor son las dos formantes, abscisa y ordenada, de esta inusual coordenada del punto W.
El punto W es la única coordenada disponible, en este área de 144 unidades de altura, que equivalen a 2,976 metros, de los 3,18 metros de la altura actual del lienzo de Las Meninas.
Estamos analizando, pues, puntos concretos situados debajo del enganche para lámpara más elevado, y ha surgido de esta observación la prueba geométrica que ratifica la importancia de este punto W.
Al final del primer capítulo del Sefer Yetzirah se atribuyen los orígenes del universo a los diez Sefirot, y, conjuntamente, se explica cómo se propaga el Aliento del Dios Vivo a partir de la Sefira nº 1, Kether, la Corona, la cual establece en el mundo; el espíritu, la voz y la palabra, más el centro de las seis direcciones del espacio.
Es, por tanto, en la coordenada del punto R : [0, 62], en el techo de Las Meninas, donde se localiza el punto cero de la contracción de la luz divina, y se rememora, desde siempre, uno de los versos más famosos de la Torah:
La respuesta de Dios a Moisés cuando le pregunta su nombre.
El nombre divino de esta Sefira se halla en Éxodo 3:14.
Y respondió Dios a Moisés:
YO SOY EL QUE SOY
|
|
Eheieh Asher Eheieh
El encuentro con el lugar de la revelación del nombre de Dios a Moisés en este óleo no sólo posee una profunda intención teológica, sino, que desatado el nudo gordiano que escondía sus dos cabos, resuelve, además, un enigma velazqueño considerado hasta ahora irresoluble.
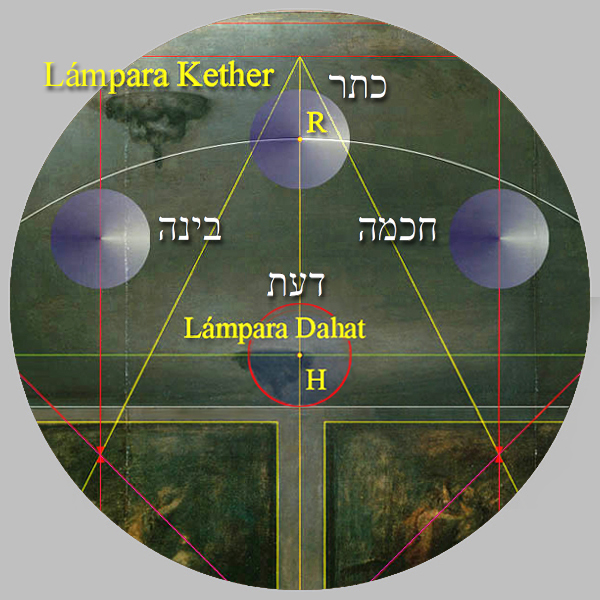 |
Primer nivel del Árbol Sagrado
עולם אצילות - Olam Atzilut |
|
|
El crecimiento proporcional de la espiral consolidada sobre la superficie de Las Meninas viene a demostrar:
La utilidad de la cuadrícula de 144 X 144 unidades llamada Línea de acotación.
La sincronizada inclinación del tiento.
La posición de la Lámpara Kether.
El punto medio, W, en la ascensión del tiento hacia el centro de la Sefira nº 1 Kether.
La posición del centro de la Sefira nº 10 Malkhut.
La línea de tierra de Las Meninas, que corresponde al vector YZ.
Y un algo más que nos remite a un estipulado propósito:
|
Simbólicamente, este punto medio y anatómico del cuerpo de la Infanta Margarita de Austria, marca el centro reservado de los elegidos, en todos los casos, una imagen e identidad exclusiva de la verdadera semilla de los reyes del mundo, tal y como en la tradición europea el Emperador se situaba, siempre, en el lugar central en las ceremonias. |
|
|
|
|
El ajustado recorrido de la espiral que detallamos pocas palabras bastan para definirlo mejor.
Una gran enseñanza del fulminante paso del tiempo, es decir; la imagen del eterno retorno.
La espiral, uno de los símbolos más antiguos de la humanidad, fue representada por pueblos distantes en tiempo y espacio; y se encuentran numerosos ejemplos en la cultura egipcia, cretense, mesopotámica, hindú, china, japonesa, precolombina, celta, escandinava...
Un dibujo en concordancia con la pujanza fecundadora solar y lunar; que evoca el nacimiento y el crecimiento, y promueve el viaje de regreso del alma a su origen entre otros distintos significados.
|
|
|
|
Margarita de Austria nació en Madrid el 12 de Julio en 1651, la Infanta era, pues, del signo de Cancer; un signo zodiacal que en los grabados del Hombre del Zodiaco se representa como un cangrejo adherido al pecho que preside al corazón, por lo que se hace necesario destacar este auspiciado punto anatómico por distintas razones, además del color rojo sangre, para iniciar la curva espiral sobre el lienzo de Las Meninas.
|
|
|
|
Velázquez, no sólo deja pintado en manchas rojas la decoración que lleva en el pecho la Infanta, sino que le dio forma de corazón.
El Árbol de la Vida, también conocido como
Árbol Sefirótico, se compone de diez emanaciones espirituales, a través de las
cuales el soplo divino dio vida a todo lo existente, pero en
Las Meninas
desvela el propósito del
espacio vacío de la mitad superior de este óleo, donde,
además de contener aire, Diego Velázquez, como eminente Aposentador y pintor del
rey, aquí alojó, en la primera esfera denominada Kether, lo más
soberano de la monarquía teocrática: La Corona.
En consecuencia; ahora es visible en el óleo de Las Meninas el enlace curvilíneo que conecta la verdadera semilla del Reino con su Corona, que retorna una y otra vez al mismo punto en el viaje espiritual hacia la vida eterna.
Lo superior
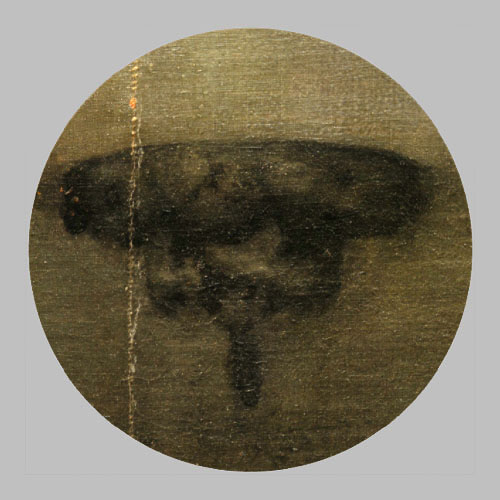
Lámpara Kether - La Corona
|
Eheieh - Yo existo
Kether - Corona - כתר |
|
 |
|
|
La Lámpara Kether representa la imagen del cumplimiento y finalidad de la empresa que el pintor ha llevado a cabo.
Entendemos, pues, que cualquier noción sobre la divinidad es imprecisa, y, aunque se logre una imagen que la haga inigualable, tenemos en su contra, como muestra los muchos ejemplos de las distintas formas e ideas que el hombre ha tenido de lo divino, que cuanto más intuitivo y concreto es el concepto de Dios más próximo y parecido es al mismo hombre.
El método que aporta la Kabala, al conocimiento de Su evidencia, sorprende al investigador por sus prácticas y enseñanzas.
|
El Dios oculto corresponde en la Kabala hebrea a Ain, literalmente la Nada, en el sentido del No-Ser, que a su vez equivale al Tao, nombre que no puede ser nombrado de la metafísica taoísta. |
|
צִמְצוּם Tsimtsum
Reducción, restricción, hacer algo pequeño y limitado en tamaño, cantidad, rango, potencia... |
|
La teoría del Tsimtsum, צםצום, introducida por Isaac Luria en el siglo XVI, explica, pues, el fenómeno de la contracción de la luz divina con el objetivo de permitir la creación, la cual se manifiesta, pues, a través de los 10 Sefirot del Árbol de la Vida.
Y se entiende, que más allá, y por encima de toda contemplación humana, está Dios tal y como Él es en sí mismo, el incognoscible Ain Sof, אין סוף, y su luz infinita Aur, אוֹר.
|
|
|
|
Diego Velázquez se valió, pues, del Árbol Sagrado de la Vida, conocido como el Rostro místico de Dios, para que su imagen latente gobernase toda su creación artística, la cual se distancia, sin embargo, del antropomorfismo divino habitual, al que siempre se le ha atribuido apariencia o cualidades humanas.
Según la Kabala, en la primera Sefira Kether se hallan; el Espíritu, la Voz y la Palabra del Dios viviente, que consolidarían, pues, al Espíritu Santo, aunque para el caso del pintor Velázquez esta Sefira aludiría al punto culminante de la secreta misión que ha llevado a cabo.
Y, como hemos ya comentado, el tiento, apuntando al techo de la Habitación del Príncipe, da entrada a un mundo espiritual con el fin de revelar lo invisible, mientras que el pincel dirigido hacia el suelo en la mano derecha del pintor, en respuesta, da fe de que se nace de la tierra, y que, después de la liberación del alma, el cuerpo retornará a ella.
|
|
En esta imagen se percibe la absoluta coordinación de este pequeño entramado de líneas;
Como se puede apreciar están conectados en un mismo punto en el aire de la Habitación del Príncipe, de modo, que este esbozo revela una Geometría Sagrada inherente a esta obra maestra.
El tiento que el pintor sujeta en su mano izquierda está dirigido hacia el techo, y establece contacto con la coordenada del punto R, centro de la Sefira nº 1, Kether, La Corona.
Y manifiestamente, la coordenada del punto R: [0, 62] y el valor numérico 620, de la palabra hebrea Kether, son cifras primas hermanas.
El nombre divino de esta Sefira se halla en Éxodo 3:14.
Y respondió Dios a Moisés:
YO SOY EL QUE SOY
Eheieh Asher Eheieh |
|
|
Aclaremos, pues, que el contacto del tiento, que sujeta Diego Velázquez en su mano izquierda, con el centro de la primera Sefira Kether se lleva a cabo en el punto primigenio, o simplemente el punto, n'kudoh r'shonoh, נקודה ראשונה, y conocido también como n'kudoh p'shutoh, נקודה פשוטה.
En esta misma línea de filosofía hermética, el humanista inglés Roberti Fludd, alias DE FLVCTIBUS, en su libro: Philoſophia ſacra et vere Chriſtiana Seu Meteorologia Cosmica. Francofurti, 1626, analiza el concierto entre la parte física del hombre, arraigada a la naturaleza, y la parte anímica e inmortal, unida a Dios.
|
+. Oscuridad absoluta. a. Luz, la primera criatura. b. La primera mezcla de luz y oscuridad. c. Luz. d. Agua. 2. Oscuridad o segundo grado de composición simple. e. Fuego. f. Aire. g. e. Agua. 4. Tierra: Raíz. 2. Cuadrado. 4. Así como el número binario es la raíz material, de la cual se deriva el primer cuadrado que indica los 4 elementos, así también en la producción de cuerpos perfectamente mezclados existen tantos grados, en el movimiento de la naturaleza, desde el cuadrado del 4º elemento, hasta el cubo del elemento perfectamente mezclado, todos los cuales deben llamarse cuerpos imperfectamente mezclados, ya que progresan desde la simple mezcla de elementos hacia la mezcla; por lo tanto, la progresión del cuadrado al cubo es de este tipo. |
|
|
|
+. Tenebræ abſolutæ. a. Lux prima creatura. b. Prima mixtio lucis cum tenebris. c. Lux. d. Aqua. 2. Tenebræ ſeu ſecundus compoſitionis ſimplicis gradus. e. Ignis. f. Aer. g. e. Aqua. 4. Terra : Radix. 2. Quadratum. 4. Vbi numerus binarius eſt radix materialis, ex qua primun quadratum. 4. elementa indicans deriuatur, ita etiam in corporum perfecte mixtorum productione totidem gradus interſunt, in motu naturæ, à quadrato ſeu 4. elementis, ad cubum ſeu elementarum perfecte miſtum, qui omnes gradus corpora imperfecte miſta reuera ſunt dicenda, vtpote qui à ſimplicitate elementorum mixtionem verſus progrediuntur, progreſſio igitur à quadrato ad cubum eſt huiuſmodi. |
|
|
Desde Kether, pues, la exaltación sefirótica desciende hasta Malkhut, la Sefira nº 10, que en el lienzo de Las Meninas se materializa en la jarrita de arcilla roja que la Infanta Margarita de Austria sujeta con su mano derecha.
Lo inferior
Malkhut - El Reino
|
|
Adonai Ha Aretz - Señor de la Tierra
מלכות - Malkhut - Reino |
X |
Malkhut |
מלכה |
Reino |
Malkhut es la esfera más tangible del acto de la manifestación cabalística, y, también, el Santo Grial de los buscadores.
Y cierto es que a la humilde arcilla de la jarrita roja de Tonalá le acompaña, pues, un innegable propósito iconográfico que garantiza una hipótesis inicial, que, a día de hoy, ninguna investigación ha planteado, a tenor de las muchas explicaciones que existen de esta obra de arte.
|
|
|
|
Aclararemos el resumen de la idea; vemos que es la menina Agustina Sarmiento la que ofrece a la Infanta Margarita, en una salvilla de plata, una jarrita de arcilla roja que simboliza la Sefira nº 10, Malkhut, es decir; el Reino, por tanto es ella la que pone en juego la idea fundamental, y asume, pues, una notoria responsabilidad de lo que se dé o brinde a la futura heredera por encargo de su majestad el rey:
La cosagración de la heredera [4].
Cuyo aval estaba preservado dentro de la simbología de los 10 Sefirot.
A
la Infanta, como a todo participante relevante de esta composición pictórica, le
corresponde una letra hebrea en particular, exactamente la letra
simple Tet, novena letra del
alefato, cuyo significado es:
Rabí Rahumai ha dicho que el vientre es como la letra Tet [5].
La letra
Tet, de valor 9, corresponde a los 9
meses del embarazo, y su forma se asemeja a un vientre o útero, aunque su
ideograma sea la serpiente, y
de acuerdo con Athanasius Kircher
le correspondería el siguiente significado:
9
ט
Teth, declinatio, exhibet nomen Dei
שדי Sadai, & Sephiram nonam
יסוד,
id eſt,
fundamentum;
ei congruentes ſunt כרובים Cherubim, ſeu Angeli; & influuntur de
virtute
Dei per medium intelligentiæ octaui ordinis, & eâdem virtute influunt in
inferiora.
9
Tet, rechazo, presenta el nombre de Dios שדי Sadai, y la novena Sefira
ישוד, es decir, el Fundamento; A esta Sefira le corresponde los
Querubines, o Ángeles; que fluyen del poder de Dios por medio de la
inteligencia de octavo orden, y por el mismo poder fluyen hacia los
inferiores
Tomus Secundus. GYMNASIVM.
ROMÆ - Anno M DC LIII.

Página 226 - CLASSIS IV. CABALA HEBRÆRVM
- CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI.

DE DIVISIONE
En mayo de 1656, el hijo bastardo del rey Felipe IV, Juan José de Austria, joven lleno de energía y sin ninguna experiencia política, fue nombrado gobernador de Flandes para hacer frente a la posible ofensiva anglofrancesa, y, en menos de dos meses de su llegada, obtuvo una fulminante victoria el 16 de Julio ante el ejército francés en el Sitio de Valenciennes.
 |
|
Joannes Auſtriacus Philippi IV Hiſpaniarum Regis filius Belgii Gubernator
Detalle del Asedio y Socorro de Valenciennes
David Teniers el joven - 1656
Royal Museum of Fine Arts - KMSKA. Antwerp |
Esta batalla, que había durado un cuarto de hora, suscitó una oferta de Francia de paz, que Felipe IV, junto al Consejo de Estado, animados por el éxito de sus armas, hizo fracasar las negociaciones 83 días antes de que se presentaran en sociedad Las Meninas de Velázquez el 7 de Octubre de 1656.
Y se reconoce, pues, la designación de esta jornada por distintos motivos;
Hagamos un esfuerzo y preparémonos para desbloquear el mundo interno de Las Meninas, y veamos con lupa en que consiste la filosofía de inmortalizar una histórica jornada:
Desde el mundo de la Kabala al día del Sábado, día en el que se manifiesta el Árbol Sagrado de la Vida.
De acuerdo con la cronología bíblica la Creación del Mundo tuvo lugar el 7 de Octubre del 3761 a.c. [6].
El año 1656, después de la Creación, representa, pues, el año del Diluvio Universal [7].
Desde el contexto de la Monarquía Austria a la batalla naval y victoria de Lepanto.
Desde el mundo Católico a la fiesta del Rosario.
El séptimo aniversario de la boda del rey Felipe IV que cayó en Sábado [8].
Desde el punto dinástico la satisfacción de una reina, ante el fruto de sus difíciles gestaciones, en el día de la Jura de su hija.
Desde el tema pictórico de este lienzo a la posible heredera de los reinos de España.
De acorde al pintor la demanda de nobleza y a la Cruz de Santiago que Velázquez se pinta en el pecho.
Desde el lado astrológico a la conjunción planetaria de los planetas regentes de los monarcas el 3 de Octubre de 1656.
El 3 de Octubre es el mismo día del año que el de la muerte de la reina Margarita de Austria, la madre de Felipe IV [9].
El día 3 de Octubre de 1656 es el equivalente a 15 Tishri 5417, el primer día de la fiesta de los tabernáculos llamada Sukot o Scenopegia, y popularmente conocida como la fiesta judía de las Cabañas.
y, para finalizar esta lista, añadir que el total de la suma de las cifras de la efeméride de esta obra maestra da el mismo resultado que el valor de la suma de las cuatro letras del Tetragrama divino.
|
|
7
de Octubre de 1656 & Nombre de Jehovah
Oficiosamente, en ocasión de su primer cumpleaños, la Infanta Margarita ya había sido designada esposa del futuro emperador Leopoldo I en 1652 cuando se representó en Viena la ópera la Gara, sin embargo, en el año 1656, ante la falta de un heredero varón, la reina Mariana de Austria siempre se hubiera decantado, como pretendiente al trono, por su única hija Margarita, pero estas expectativas se oponían al derecho de sucesión de Maria Teresa, aunque por su compromiso con el Rey de Francia ya estaba descartada.
De manera, que en Las Meninas se escenificó, ante la posibilidad de que la reina madre enviudara, una hipotética jura que proclamase a la Infanta Margarita heredera, un deseo en esos momentos irrealizable que la reina subsanó pariendo un varón un año después.
La derrota de Valenciennes había empujado a la Corte francesa a tomar la resolución de enviar secretamente al Marqués de Lionne a España con órdenes de ofrecer la Paz a sus enemigos, no obstante, aunque España había deseado esta Paz durante mucho tiempo, Felipe IV se negó a entrar en negociación hasta que el Rey de Francia no hubiera consentido la completa restitución del Príncipe de Condé, y, además, rechazó la oferta de matrimonio, de Luis XIV con su hija María Teresa, por temor a que la Corona de España cayera en manos de un rey Borbón ante la falta de un heredero varón.
Y ahora se entiende, pues, que en estos momentos la euforia del rey de España era tan sobrada que se conjura en el alegato de esta obra maestra al promover la idea de una heredera, aunque, al mismo tiempo, también deberíamos contar con la palabra latina declinatio, que se traduce por rechazar un ofrecimiento, o una responsabilidad, y en especial rechazar cortésmente una invitación, sin embargo, el cabello dorado de la Infanta augura su responsabilidad futura, ya que, en la división de la pared del fondo en doce partes iguales, a la Infanta Margarita le corresponde el signo de Leo, cuya constelación rige el rey de los planetas, el Sol,
| Personaje |
Letra hebrea |
Caligrafía |
Característica |
Letra latina |
Signo del Zodiaco |
Planeta |
Casa Astrológica |
| Infanta Margarita de Austria | Tet |
|
Audición | T |
 Leo Leo |
Sol | Casa V - Filii - Los Hijos |
|
|
Y como toda letra hebrea, la forma de la Tet expresa una idea en particular, Mario Satz la define como:
La vida oculta tras el helicoide del ombligo.
Y añade en otro renglón una lectura más amplia:
| La Kabala convierte al nueve en la letra Tet, el ombligo, el centro, la espiral cósmica. El nueve anuncia a la vez que un fin, el comienzo de una nueva dimensión; es el número germinal [10]. |
El ombligo vincula al ser humano con su origen.
המליך אות ט' בשמיעה
וקשר לו כתר וצרפן זה בזה וצר
בהם אריה בעולם ואב בשנה
וכוליא שמאלית בנפש זכר ונקבה׃
Hizo
reinar la letra Tet,
y
le ató una Corona.
Combinó
una con otra
y
formó con ellas:
Leo
en el Universo,
´Av
en el Año
y
el riñón izquierdo en el Alma;
masculino
y femenino.

Sefer Yetzirah
- Capítulo 5:8
En la división en doce partes iguales de la pared del fondo la Infanta Margarita de Austria se sitúa, pues, en el signo de Leo, cuyo planeta corresponde al Sol, una estratégica posición que responde al ideal del príncipe solar en todas las monarquías europeas modernas.
En Las Meninas la Infanta Margarita se haya identificada con el astro rey, de manera, que como el Sol, permanentemente brillase en lo más alto de una España que era el Imperio en el que nunca se ponía el Sol.
El signo de Leo EL SOL - CARTA XIX
Del Tarot de Francesco Sforza

El Sol, como rey y señor de todos los planetas, da luz a los siete astros restantes, incluido el planeta Tierra:
|
El Sol tiene dominio ſobre los Reyes, y Grandes Señores, ſobre los hombres graves, y magnánimos; ſobre los de grandes conſejos, y magnificos; y finalmente, ſobre todos aquellos, que son Conſiliarios de Reyes, y grandes Señores. |
Lunario Perpetuo - 1606 - Gerónimo Cortés.
Respecto a la letra Tet comenta el sefardí Isaac Atias en 1627 [11]:
|
Y aun ponderando los Theologos, la cuenta de Iſrael, y la correſpondencia de la Ley, recopilada toda en el Decalogo, dizen que los Leuitas conſagrados al Sñor, eran 22. mil y 22. es el numero de las letras de la Ley, las quales ſe hallaran todas en el Decalogo, excepto la letra Teth. (y en los ſegundos del Deuteronomio ella tambien) por secreto inexplicable ... |
|
לא יהיה־לך אלהים אחרים על־פני׃ |
|
20:3 | |
|
לא תעשׂה־לך פסל וכל־תמונה אשׁר בשׁמים ממעל ואשׁר בארץ מתחת ואשׁר במים מתחת לארץ׃ |
|
20:4 | |
|
לא־תשׁתחוה להם ולא תעבדם כי אנכי יהוה אלהיך אל קנא פקד עון אבת על־בנים על־שׁלשׁים ועל־רבעים לשׂנאי׃ |
20:5 | ||
|
ועשׂה חסד לאלפים לאהבי ולשׁמרי מצותי׃ |
20:6 | ||
|
לא תשׂא את־שׁם־יהוה אלהיך לשׁוא כי לא ינקה יהוה את אשׁר־ישׂא את־שׁמו לשׁוא׃ |
20:7 | ||
|
זכור את־יום השׁבת לקדשׁו׃ |
20:8 | ||
|
שׁשׁת ימים תעבד ועשׂית כל־מלאכתך׃ |
20:9 | ||
|
ויום השׁביעי שׁבת ליהוה אלהיך לא־תעשׂה כל־מלאכה אתה ובנך־ובתך עבדך ואמתך ובהמתך וגרך אשׁר בשׁעריך׃ |
20:10 | ||
|
כי שׁשׁת־ימים עשׂה יהוה את־השׁמים ואת־הארץ את־הים ואת־כל־אשׁר־בם וינח ביום השׁביעי על־כן ברך יהוה את־יום השׁבת ויקדשׁהו׃ |
20:11 | ||
|
כבד את־אביך ואת־אמך למען יארכון ימיך על האדמה אשׁר־יהוה אלהיך נתן לך׃ |
20:12 | ||
|
לא תרצח׃ |
20:13 | ||
|
לא תנאף׃ |
20:14 | ||
|
לא תגנב׃ |
20:15 | ||
|
לא־תענה ברעך עד שׁקר׃ |
20:16 | ||
|
לא תחמד בית רעך לא־תחמד אשׁת רעך ועבדו ואמתו ושׁורו וחמרו וכל אשׁר לרעך׃ |
20:17 |
|
|
Estos 14 versículos se componen, pues, de un total de 620 letras hebreas.
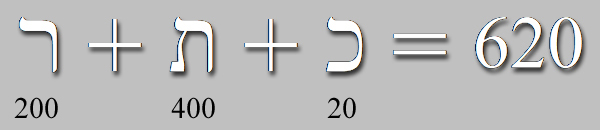 |
|
|
Las tres letras consonantes del nombre de la Sefira nº 1 Kether suman 620; número que equivale también al total de los preceptos que Dios ordenó al pueblo de Israel, y, como hemos comentado, corresponde, además, a la misma cantidad de letras que componen la lectura de los 14 versículos de los Diez Mandamientos en el capítulo 20 del Éxodo; desde el versículo 3 hasta el versículo 17 inclusive.

El techo de Las
Meninas
David Vidal ben Salomoh, célebre talmudista y notable médico, músico y poeta, nació en 1467, probablemente en Toledo, escribió un libro titulado Corona de la Ley, כתר תורה, en el que analiza los 613 preceptos de la Ley de Moisés, y los siete preceptos particulares que prescriben los maestros Rabinos.
Las 613 mitzvot, o preceptos de la Torah Escrita, más los 7 mitzvot de la Torah Oral hacen un total de 620.
El secreto de los 620 mandamientos es la conexión entre el techo; Kether, con el suelo; Malkhut.

La Espiral de Velázquez
Habría
que añadir que Las Meninas acepta geométricamente otra espiral
áurea que denominamos La Espiral del Pintor.
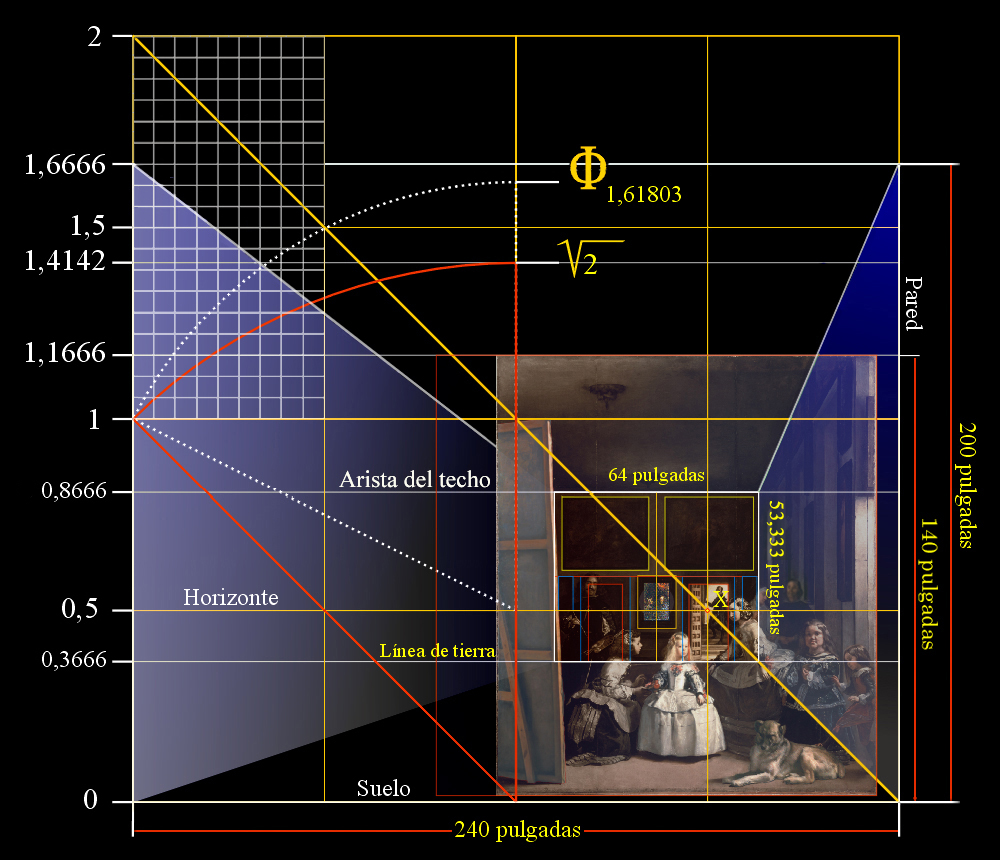
Esta rejilla de trabajo consiste en una cuadrícula de 4 x 4, que equivale a una rejilla de 240 por 240 pulgadas.
La pulgada castellana equivale a 0,02325 metros, por tanto, hablando en metros, esta cuadrícula mediría 240 pulgadas x 0.02325 metros por pulgada de lado que es igual a 5,58 metros.
 |
|
|
Estos diagramas son lo suficientemente exactos para entender el orden matemático que mantuvo el maestro en todo momento de su creación.
El pintor centra el eje del escenario de Las Meninas de acuerdo a una potente diagonal, y asigna una específica función a cada elemento o personaje a lo largo de la línea del tiempo u horizonte.
Efectivamente, la línea de horizonte es un símil de la eclíptica, es decir; del factor tiempo en Las Meninas.
 |
|
|
La serie de los números de Fibonacci es la referencia de La Espiral del Pintor, pero hay un cambio en la serie que señalamos para Velázquez.
Esta diferencia numérica se puede comprobar en la siguiente tabla:
| Serie Fibonacci | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | |
| Pulgadas | 0,8888 | 0,8888 | 1,7777 | 2,6666 | 4,4444 | 7,1111 | 11,5555 | 18,6666 | 30,2222 | 48,8888 | 79,1111 | 128 | 207,1111 | |
| Serie Velázquez | 1/2 | 1/2 | 2 | 2 y 1/2 | 4 y 1/2 | 7 | 11 y 1/2 | 18 y 1/2 | 30 | 48 y 1/2 | 78 y 1/2 | 127 | 205 y 1/2 |
|
|
|
|
|
|
El punto medio del Árbol
El
tamaño de los cuadraditos que hemos usado para la construcción de
La Espiral
de
Las Meninas ha sido dada
por la particular característica de la acotación geométrica de la rejilla de 50 cuadraditos de
lado, que se extiende hasta lo que hemos dado en llamar:
Límite de la rejilla de 150 unidades.
Tipos de cuadrículas sobre la superficie de Las Meninas:
 |
|
Hablamos, pues, de una cuadrícula geométrica superpuesta a la superficie del lienzo de Las Meninas que ha rescatado del olvido las antiguas medidas de longitud castellanas.
|
Acotación geométrica |
Unidades |
Pulgadas |
Abscisa X |
Ordenada Y |
|
Línea de acotación Límite de la rejilla de 150 unidades Límite de la rejilla de 152 unidades |
144 x 144 150 x 150 152 x 152 |
128 x 128 133 y 1/3 x 133 y 1/3 135 y 1/9 x 135 y 1/9 |
0 |
0 |
|
Borde del orillo del lino original |
155,25 x 155,25 |
138 x 138 |
0 |
0,375 |
|
Pared del Fondo |
72 x 60 |
64 x 53 y 1/3 |
0 |
0 |
|
|
Analicemos, pues, la cuadrícula que hemos dado en llamar:
Límite de acotación.
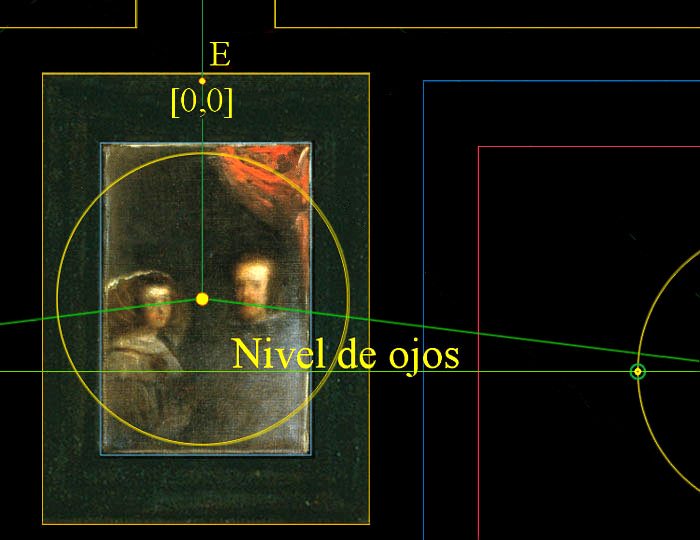
Esta acotación geométrica corresponde a un cuadrado de 144 x 144 unidades, equivalente a un cuadrado de 128 x 128 pulgadas de lado, cuyo centro depende del punto E.
 |
|
|
No hemos subrayado la capacidad reguladora, e indispensable ayuda, que aporta esta cuadrícula en la medición de la anchura exacta de la pared del fondo de Las Meninas, y es ahora cuando la destacamos por su cualidad geométrica.
En el siguiente ejemplo comprobaremos que la cuadrícula denominada: Línea de acotación, de 144 X 144 unidades, regula el tamaño de la anchura exacta de la pared del fondo, y, además, acomoda las dos esquinas inferiores del suelo de esta misma pared en los vértices Z e Y.
 |
|
|
Tenemos que L es el punto medio del Árbol Sagrado, que corresponde al vértice superior del triángulo YLZ.
El punto de intersección de las tres medianas del nuevo triángulo ÝLZ´ es el punto k, es decir, su Baricentro, que se sitúa en el perímetro de la Sefira Malkhut, El Reino.
El punto L tiene por coordenadas: [0, 12], ahora bien, observemos en la imagen el vector ÝZ´, correspondiente al lado inferior del cuadrado que llamamos; Línea de acotación, que se halla, a su vez, implicado como base del triángulo, ÝLZ´, donde dos de sus medianas; ÝZ y Z´Y, además, desvelan las dos esquinas del suelo de la pared del fondo.
Recordaríamos, pues, que la cuadrícula Límite de acotación equivale a un cuadrado de 128 x 128 pulgadas de lado, mientras que el ancho de la pared del fondo pintada de Las Meninas mide exactamente la mitad del tamaño del lado de esta misma rejilla geométrica, es decir; 64 pulgadas.
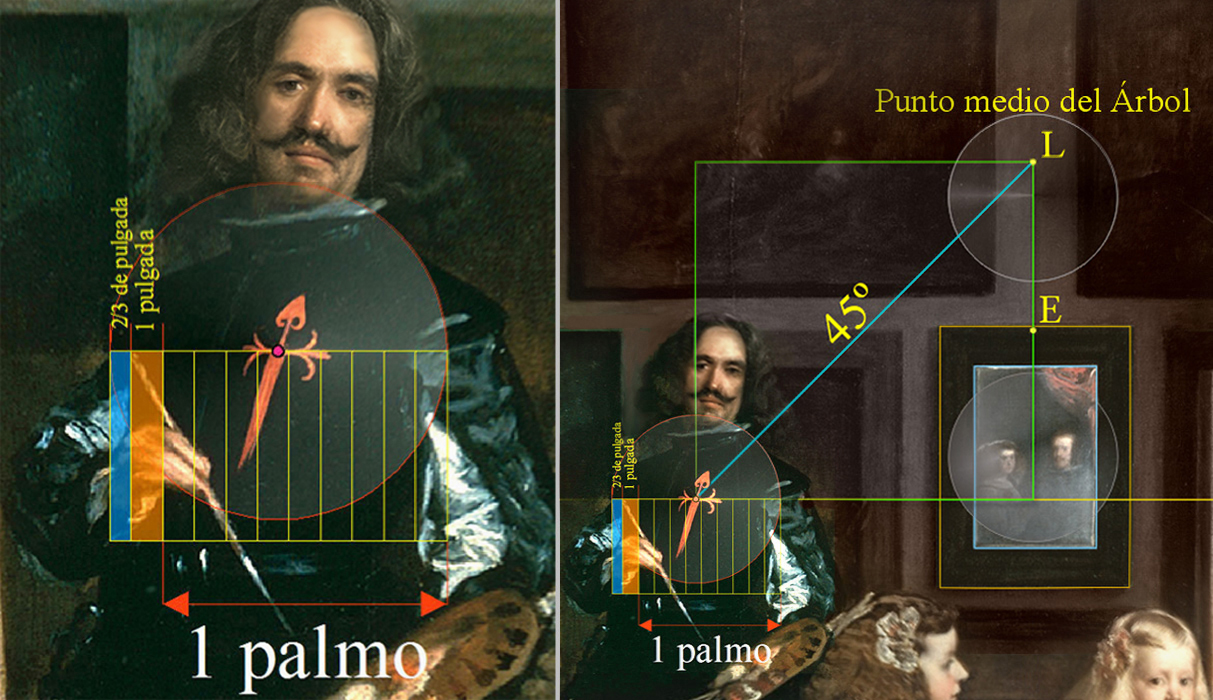
Y existe otro modo de localizar el punto L si trazamos un vector, con una inclinación de 45º, desde la cruceta del Hábito de la Cruz de Santiago hasta el pilar Central del Árbol Sagrado, localizaremos, de nuevo, el punto medio L, que tiene por coordenada: [0, 12].
 |
|
|
En la pensada posición de la cruceta de la Cruz del Hábito de Santiago estaría instalado, pues, un eficaz conjuro en el pecho del pintor, que ratificaría, desde el leb, לב, corazón, el conocimiento cabalístico del maestro Velázquez.
La palabra hebrea leb alude a los treinta y dos senderos de la Sabiduría del Árbol de la Vida, y el número 32 se compone de las siguientes letras:
| letra hebrea | grafía | valor numérico |
| Lamed |
 |
30 |
| Bet |
 |
2 |
Es decir; לב se lee leb, y se traduce por corazón, pero, lo que es más importante; son la última y primera letra de la Torah, por lo que dicha palabra encierra la totalidad de la revelación escrita desde el principio de Israel:
En el principio... Israel.
Bereshit... Israel.
 |
Consideraremos este recado como un episodio velazqueño inconfesable, aunque, a su vez, se revela el Corazón, y punto medio, del sacro símbolo con la ayuda de un vector inclinado a 45º, lo cual explica, pues, que el pintor, dependiendo de sí mismo, reivindicó su verdad atrincherado en el etéreo peso de su consciencia, y, de hecho, con exactitud reseñó la intención de su propósito.
Las coordenadas geométricas usadas por Velázquez confirman la armonía entre los distintos contenidos del óleo de Las Meninas, y el porqué del punto medio W, en el recorrido del tiento hacia el centro de la Sefira Kether en el punto R, a la misma altura de la garganta del pintor.
notas a pie de página
1 - La república de Pisa, a finales del siglo XII, era una gran potencia comercial con delegaciones en todo el norte de África, y es, precisamente, en una de estas delegaciones, en la ciudad argelina de Bugía, donde uno de los hijos de Bonaccio, el responsable de la oficina de aduanas en la ciudad, Leonardo, es educado por un tutor árabe en los secretos del cálculo posicional hindú, un secreto que acabaría siendo uno de los más importantes regalos del mundo árabe a la cultura occidental:
Nuestro actual sistema de numeración.
Leonardo de Pisa, Fibonacci, nombre con el que pasará a la Historia, aprovechó sus viajes comerciales por todo el mediterráneo; Egipto, Siria, Sicilia, Grecia..., para entablar contacto con los matemáticos más notables de la época, y descubrir los Elementos de Euclides, que tomará como norma de estilo y rigor.
De su deseo de poner en orden todo cuanto había aprendido, de Aritmética y Álgebra, en 1202 brinda a sus colegas comerciantes un potente sistema de cálculo, cuyas ventajas él había ya experimentado: El Liber Abbaci, la primera Summa matemática de la Edad Media.
En este libro aparecen, por primera vez en Occidente, las nueve cifras hindúes y el signo del cero.
Leonardo de Pisa en su obra proporciona reglas claras;
para realizar operaciones con números enteros y fracciones,
de la regla de tres simple y compuesta,
de normas para calcular la raíz cuadrada de un número,
así como instrucciones para resolver ecuaciones de primer y segundo grado.
Después de los siglos Fibonacci es más conocido entre los matemáticos por una curiosa sucesión de números:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
que colocó en el margen de su Liber Abbaci junto al conocido problema de los conejos, que más que un problema parece un acertijo de matemáticas recreativas.
La pregunta al problema diría así:
¿Cuántas parejas de conejos se producirán en un año, comenzado con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo mes?
|
Parium 1 Primus 2 Secundus 3 Tercius 5 Quartus 8 Quintus 13 Sestus 21 Septimus 34 Octauus 55 Nonus 89 Decimus 144 Undecimus 233 Duodecimus 377 |
|
Quot paria coniculorum in uno anno ex uno pario germinentur.
Qvidam posuit unum par cuniculorum in quodam loco, qui erat undique pariete circundatus, ut sciret, quot ex eo paria germinarentur in uno anno: cum natura eorum sit per singulum mensem aliud par germinare; et in secundo mense ab eorum natiuitate germinant. Quia suprascriptum par in primo mense germinat, duplicabis ipsum, erunt paria duo in uno mense. Ex quibus unum, scilicet primum, in secundo mense geminat; et sic sunt in secundo mense paria 3; ex quibus in uno mense duo pregnantur; et geminantur in tercio mense paria 2 coniculorum; et sic sunt paria 5 in ipso mense; ex quibus in ipso pregnantur paria 3; et sunt in quarto mense paria 8; ex quibus paria 5 geminant alia paria 5: quibus additis cum parijs 8, faciunt paria 13 in quinto mense; ex quibus paria 5, que geminata fuerunt in ipso mense, non concipiunt in ipso mense, sed alia 8 paria pregnantur; et sic sunt in sexto mense paria 21; cum quibus additis parijs 13, que geminantur in septimo, erunt in ipso paria 34; cum quibus additis parijs 21, que geminantur in octauo mense, erunt in ipso paria 55; cum quibus additis parjis 34, que geminantur in nono mense, erunt in ipso paria 89; cum quibus additis rursum parijs 55, que geminantur in decimo mense 144; cum quibus additis rursum parijs 89, que geminantur in undecimo mense, erunt in ipso paria 233. Cum quibus etiam additis parijs 144, que geminantur in ultimo mense, erunt paria 377; et tot paria peperit suprascriptum par in prefato loco in capite unius anni. Potes enim uidere in hac margine, qualiter hoc operati fuimus, scilicet quod iunximus primum numerum cum secundo, uidelicet 1 cum 2; et secundum cum tercio; et tercium cum quarto; et quartum cum quinto, et sic deinceps, donec iunximus decimum cum undecimo, uidelicet 144 cum 233; et habuimus suprascriptorum cuniculorum summam, uidelicet 377; et sic posses facere per ordinem de infinitis numeris mensibus. |
Página 285 - SCRTTI DI LEONARDO PISANO - Matematico del Secolo Decimoterzo. Pubblicati da Baldassarre Boncompagni. Volume I Liber Abbaci. Roma - MDCCCLVII.
2 - La Espiral de la Sucesión de Fibonacci no es una espiral de Arquímedes ni tampoco una espiral logarítmica, pues ninguna de las dos puede construirse con regla y compás; sin embargo, se aproxima bastante a esta última.
3 - Cada unidad en el plano que presentamos equivale a 8/9 de pulgada, que traducido al sistema métrico equivale a: -
El Pie Real de 0,279 metros dividido entre doce es igual a 0,02325 metros la pulgada, este resultado, a su vez, lo dividimos entre 9, que nos da como resultado 0,002583333 metros ó 1/9 de pulgada.
La solución de la equivalencia de 8/9 de pulgada en el sistema métrico será por tanto la multiplicación de 0,002583333 metros por 8, que es igual a 0,020666666 metros.
Más o menos 2 centímetros.
Si una pulgada vale 0,02325 metros y equivale a ------------------- 1,125 unidades.
8/9 de pulgada que es igual a 0,020666666 metros equivaldrá a --------------------- X unidades.
Hagamos esta simple regla de tres:
X = 0,020666666 metros por pulgada X 1,125 unidades / 0,02325 metros por pulgada = 1 unidad.
4 - Origen de la primera princesa de Asturias:
|
Una de las coſas mas notables para nueſtro aſſunto era, que el dicho Infante D. Henrique, y ſu eſpoſa Doña Catalina fueſſen jurados Principes de Aſturias, cuyo origen provino de eſte lance, originado de la practica uſada en Inglaterra, de que al primogenito heredero intitulaban Principe de Gales. Eſto ſe practicó en Inglaterra deſde el caſamiento de Eduardo (hijo del Rey Henrique III.) con nueſtra Infanta Doña Leonor; (hija de S. Fernando) y ahora por una reciproca correſpondencia entró el titulo de Principe en Eſpaña, caſando nueſtro heredero con Ingleſa. Fue pues la primera vez que en Eſpaña ſe oyó titulo de Principe y Princeſa, contrahido al heredero de los Reynos, en el Infante D. Henrique III. y ſu eſpoſa Doña Catalina, con el adito de Aſturias. |
|
Catalina de Alencastre fallecida en 1418 |
Página 696 - Tomo II - MEMORIAS DE LAS REYNAS CATHOLICAS - Historia Genealogica de la Casa Real DE CASTILLA, Y DE LEÓN.
P. Mro. Fr. Henrique Florez, del Orden de S. Agustin. Madrid - MDCCLXI.
5 - Apartado 84 - El Libro de la Claridad - Sefer Ha - Bahir.
|
פד. מ"ם פתוחה, מאי מ"ם פתוחה, כלולה מזכר ונקבה, מ"ם סתומה מאי, עשויה היא כמין בטן מלמעלה, והא אמר רבי רחומאי, הבטן כמין ט, ההוא דאמר כמין ט בפנים, אנא דאמרו כמין ט בחוץ׃ |
84. La Mem abierta. ¿Qué es la Mem abierta? Esta letra incluye lo masculino y femenino. ¿Y qué es la letra Mem cerrada? Es como si estuviera hecha como un vientre mirado desde arriba. Pero Rabí Rahumai ha dicho que el vientre es como la letra Tet. Él dijo que es como una letra Tet en el interior, mientras que yo digo que es como una Mem en el exterior. |
6 - En un libro dedicado a Fernando VI de Borbón, llamado el Prudente o el Justo, rey de España desde 1746 hasta 1759, cuarto hijo de Felipe V y de su primera esposa María Luisa Gabriela de Saboya, encontramos la aclaración de la fecha exacta de la Creación del Mundo:
|
3 Para Epocha de ſu computo no tomaron los Judios el principio de alguno de ſus Reyes, ni de los Chaldeos, debaxo de cuya poteſtad eſtuviero cautivos en Babylonia, ni de los Romanos Emperadores, que los dominaron deſpues; porque eligieron la Era del mundo, ſegun el calculo de ellos, no poco diſonante de la verdad Chronologia, que la antepone caſi dos ſiglos. El principio del magno periodo Judaico, llamado Epocha Judaica, y Novilunio primero Judaico, es feria ſegunda, hora quinta, y minutos ducientos y quatro, que en el computo ſe exprime con eſtos numeros: 2.5.204, deſpues del occaſo del Sol en Vr Chaldæorum; año del periodo Juliano 953, dia 7. de Octubre, Cyclo Solar I. letra Dominical F, por cuya razon el Cyclo Solar Romano, no ſe diferencia del Cyclo Solar Judaico, por todos los años del periodo Juliano. Conſta de lo dicho, que la Neomenia del primer Tiſri eſta colocada en el año 3761. antes de Christo Señor nueſtro, Lunes 7. de Octubre, 11. horas, y 204 Helakim, deſpues de medio dia. Noteſe, que Helakim es palabra Hebrea, que ſignifica minutos, de los quales la hora tiene 1080. de forma, que à vn Helakim correſponden 3. ſegundo, y 20. terceros Aſtronomicos; y aſsi vn minuto horario tiene 18. Helakim, ò minutos Judaicos: y vn Helakim, que tambien llaman punto, tiene 76. momentos. |
|
|
Página 182 - ASTRONOMIA VNIUERSAL THEORICA, Y PRACTICA, conforme a la doctrina de antiguos, y modernos Aſtronomos, con Methodo facil, y muy claros exemplos, para que los aficionados à tan ſublime Ciencia la puedan ſaber ſin voz viva de Maeſtro, y juntamente otros aſſumtos muy curioſos de Chronologia Aſtronomica, y computo Ecleſiaſtico. TOMO PRIMERO. DEDICADO AL SERENISSIMO, Y CATHOLICO PRINCIPE DE ASTURIAS N. S. DON FERNANDO DE BORBON. Gonzalo Antonio Serrano, philo-matematico, y medico en la ciudad de Cordoba, sv patria. Cordoba, 1735.
7 - Cualquier ritual serio de Kabala requiere del uso del algún tipo de invocación y momento oportuno. Llegados a este punto se hace necesaria la ayuda inestimable de algún texto sagrado.
La bíblica y erudita divisa mágica que hemos escogido, y no por capricho, se irradia desde el balcón del poder y certifica que el año de la realización de este lienzo no está elegido al azar:
Será en el capítulo XXXVIII del libro Génesis Rabbah, Génesis 11:1, donde leemos:
Y palabras únicas... [‘AHADIM] significa que proferían palabras ásperas, HADIM, cuando dijeron:
Una vez cada mil seiscientos cincuenta y seis años [1656 ] el firmamento se tambalea, así que, ¡venga!, hagámonos unos soportes; uno al Norte, otro al Sur, otro al Oeste, y éste de aquí [Babilonia] será su soporte al Este, como está escrito:
Y la tierra entera tenía una sola lengua de ásperas palabras.
ויהי כל־הארץ שׂפה אחת ודברים אחדים׃
La frase bíblica que señalamos habla de la soberbia de los descendientes de Sem, hijo de Noé, ante Dios, una vez que el Diluvio Universal tuvo lugar, que, como ya sabíamos, Le desafiaron en el caso de la construcción de la Torre de Babel.
Génesis Rabbah I. Comentario Midrásico al libro del Génesis. Luis Vegas Montaner. Facultad de Filología, Universidad Complutense de Madrid. Editorial Verbo Divino.
8 - El rey Felipe IV siempre supo en que día y año se casaba con su segunda esposa.
En una carta de Felipe IV a la Condesa de Paredes de Nava, del 28 de Septiembre de 1649, le confiesa:
y el jueves siete del mes que viene juzgo la veré y será la boda...
Página 100 - Felipe IV y Luisa Enríquez Manrique de Lara, Condesa de Paredes de Nava: Un Epistolario Inédito. Joaquín Pérez Villanueva. Salamanca, 1986.
9 - Muerte de la reina Margarita de Austria, la madre de Felipe IV:
|
El Lunes por la mañana, que fue a tres de Otubre, dia triſtiſsimo para Eſpaña, pues en el ſe le puſo eſte Sol de virtudes por el Ocaſo de ſu muerte: eſtuuimos a la cabecera de la cama de la Reyna N.S. el padre Ricardo Haller ſu confeſſor, el padre Antonio ſu compañero, el padre F. Franciſco de Arribas confeſſor de la ſeñora Infanta doña Ana: el Dotor Gamarra, Cura de Palacio: el padre Prior de S. Lorenço, y yo, rezando y diziendo algunas deuociones, y dos vezes dixe yo la Recomendacion del alma, la qual encomendò ſu Mageſtad en las manos de ſu Criador, dando dos boqueadas ſin ninguna deſcompoſicion de ſu ſemblante, el qual quedò como de vn Angel, entre las nueue y diez de la mañana (a la miſma hora que nacio) del dia y mes que he dicho del año de mil y ſeiſcientos y onze, ſiendo de edad de veinte y ſeis años nueue meſes y ocho dias. No falta quien halle miſterio en las miſmas letras del nombre de doña Margarita de Auſtria Reyna de Eſpaña y diga que deſtas letras reducidas a numero ſale cabalmente eſte de mil y ſeiscientos y onze, que fue el año en que la Reyna nueſtra ſeñora murio. En eſpirando le diximos vn reſponſo con harto ſentimiento y dolor. Y el cielo parece acudio, y ſe conformò en el ſentimiento de todos, dando el primer clamor entre eſcuras y eſpeſſas nubes con vn gran trueno que a eſte punto ſe oyò: quiza fue eſta la ſeñal que hizo aquel hijo del trueno el Apoſtol Santiago Patron de Eſpaña, que como Reyna della la ſalio a recibir haziendola primero eſta ſalua. |
Página 232 - VIDA Y MUERTE de D. Margarita de Austria. Reyna de Eſpanna. Al Rey D. Phelippe. III. N. Sr. D. Diego de Guzman. Patriarcha de las Indias, Arçobispo de Tyro, del Conso. de ſu Magd. Y del supremo de la sta. y general Inquisicion, su Capellan y Limosnero mayor. Madrid. Año M.DC.XVII.
10 - Mario Satz - Senderos en el jardín del corazón - Editorial Kairós S. A.- Marzo 1989.
11
-
Página 13 - TESORO DE PRECEPTOS – Donde se encierran las joyas de
los Seys cientos y treze Preceptos, que encomendò el Sñor à ſu Pueblo Iſrael.
Por Isaac Atias. Año 5387. En Venecia – MDCXXVII. Appreſſo Gioanne Caleoni.
|
La Kabala y Las Meninas |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |