|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fantoni tiene licencia CC BY-NC 4.0 |
|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fantoni tiene licencia CC BY-NC 4.0 |
|
|
A
finales del siglo XV,
Luca Pacioli en su libro DE DIVINA PROPORTIONE
[1],
título que hace referencia a la proporción del número áureo, escribe:
|
De ahí que entre los sabios se acostumbra a decir, según proverbio común: Aurum probatur ignis et ingenium mathematicis, es decir, que la bondad del oro la demuestra el fuego y la calidad de los ingenios las disciplinas matemáticas. Y esta sentencia pretendía expresar que el genio apto para las matemáticas lo es también para las otras ciencias (...).
(...) Platón negaba, no sin razón, la entrada a los que ignorasen la geometría en su celebérrimo gimnasio, sobre cuya puerta principal colocó, en letras grandes y bien inteligibles, una breve inscripción con estas formales palabras: Nemo huc geometriæ expers ingrediatur, es decir, que no entrase quien no fuese un buen geómetra; e hizo esto porque en la geometría se encuentra oculta toda otra ciencia. |
 |
|
Diuina proportione
Opera a tutti glingegni perſpicaci e curioſi neceſſaria Oue ciaſcun ſtudioſo di Philosophia: Proſpectiua Pictura Sculptura: Architectura: Muſica: e altre Mathematice: ſuauissima: ſottile: e admirabile doctrina conſequira: e delectaraſſi: con varie queſtione de secretiſſima ſcientia.
Divina proporción
Obra para todas las mentes perspicaces y curiosas necesaria para cada estudioso de Filosofía: Perspectiva Pintura Escultura: Arquitectura: Música: y otras Matemática: suavísima: sutil: y admirable doctrina logrará: y deleitará: con varias cuestiones de la secretísima ciencia. |
Si bien, Las Meninas están pensadas de acuerdo con la estética y leyes de óptica geométrica conocidas en el siglo XVII, sin embargo su mensaje se oculta tras toda otra ciencia, como así señaló Luca Pacioli, y Diego Velázquez expresó a la española.
Y cierto es que Velázquez compuso su obra maestra con proporción geométrica, cuya eficacia se demuestra con la ayuda de un cuadrado de 152 unidades de lado.
|
Sistema de medidas |
Anchura |
|
Altura |
|
Total de Coordenadas |
|
unidades |
152 |
× |
152 |
= |
23104 |
| Conversor: 1,125 unidades por pulgada | |||||
| pulgadas | 135,111111... | × | 135,111111... | ||
| Conversor: 0,02325 pulgadas por metro | |||||
|
metros |
3,141333... |
× |
3,141333... |
|
|
|
|
La relación de la rejilla de trabajo de 152 unidades de lado, y el valor de la constante racional de Pi de 3,141333..., de acuerdo con la pulgada castellana, certifica la dimensión matemática idónea de la rejilla maestra cuando se mide en metros.
|
CONSTANTE DE PI |
VALOR NUMÉRICO |
FRACCIÓN | DESVIACIÓN |
ORIGEN HISTÓRICO |
|
Pi actual |
3,141592654... |
π | 0 |
Valor actual |
|
Velázquez |
3,141333333... |
1178/375 | 0,000259321... |
Codificado en Las Meninas |
|
Arquímedes |
3,142857142... |
22/7 | 0,001264489... |
Utilizado en el Siglo XVII |
|
|
Esta tabla es la prueba de que la constante Pi codificada por Velázquez es la base geométrica y aritmética en Las Meninas, y lo más relevante es que esta constante se acerca al valor actual de Pi con una precisión superior a cualquier otra aproximación racional conocida en España en el siglo XVII, lo que demuestra la maestría matemática de la composición [2].
|
|
Y esta es la lista en donde descuella el pintor español, que, además, de utilizar la altura necesaria de 3,141333... metros para representar la Geometría áurea, al mismo tiempo, consolida, en un mapa de 23104 coordenadas posibles, a las diez esferas cabalistas en el transparente aire de la sala del Alcázar de Madrid representada en Las Meninas.
Según el Catálogo del Museo del Prado:
La altura actual de este lienzo es de 3,18 metros.
 |
|
|
El pintor propone todo un gran desafío de acuerdo con la lectura interior de esta pintura [3]:
La aplicación de la Geometría áurea
y la enseñanza trascendente de las diez esferas cabalísticas del Árbol Sagrado.
Una relación presente concebida desde puntos muy concretos, que, en verdad, completa la experiencia sensorial de este lienzo.
Presentamos, pues, una comprensión inmediata de una revelación extraordinaria en el Arte de la Pintura.
 |
|
|
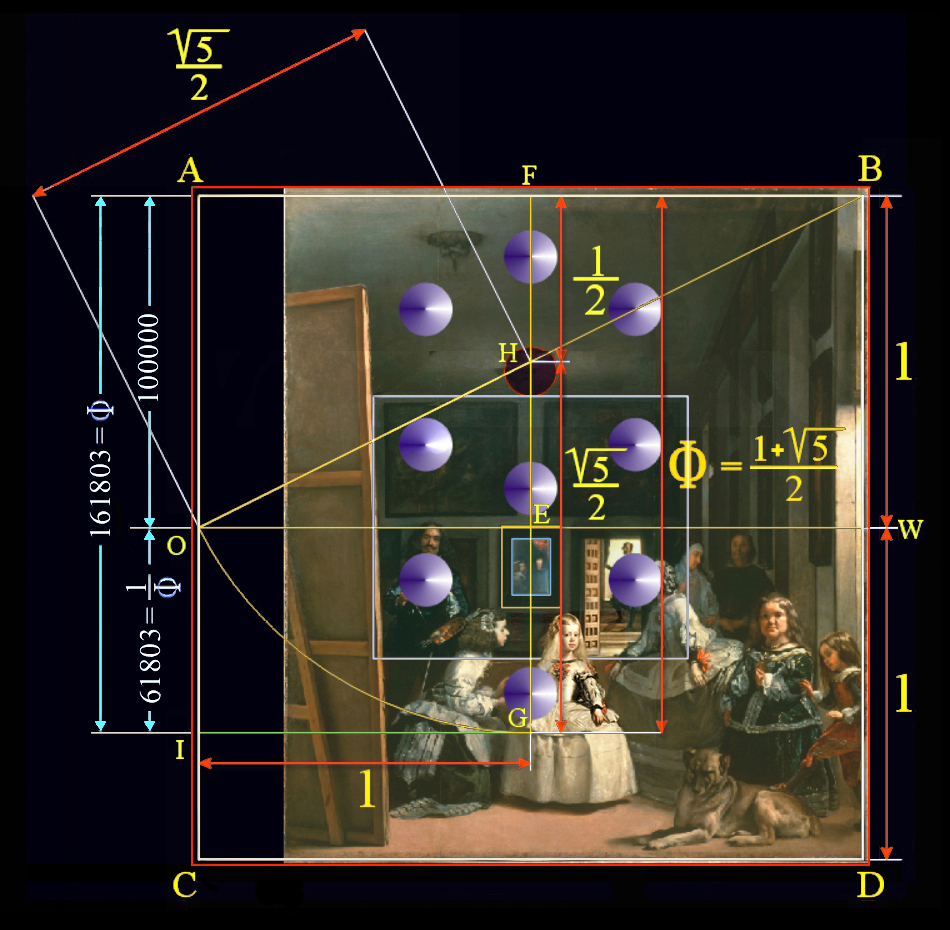
Con estas tres condiciones accederemos, pues, al plano de la Divina Proporción, pero con una ventaja adicional, ya que ahora no buscamos si está ahí, sino que estamos contemplando cómo funciona su estructura geométrica en Las Meninas.
|
|
|
|
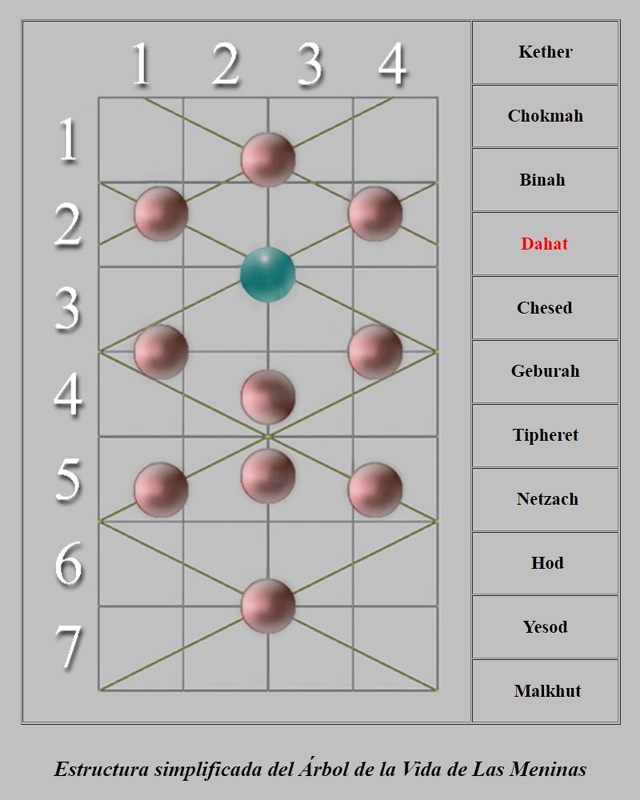
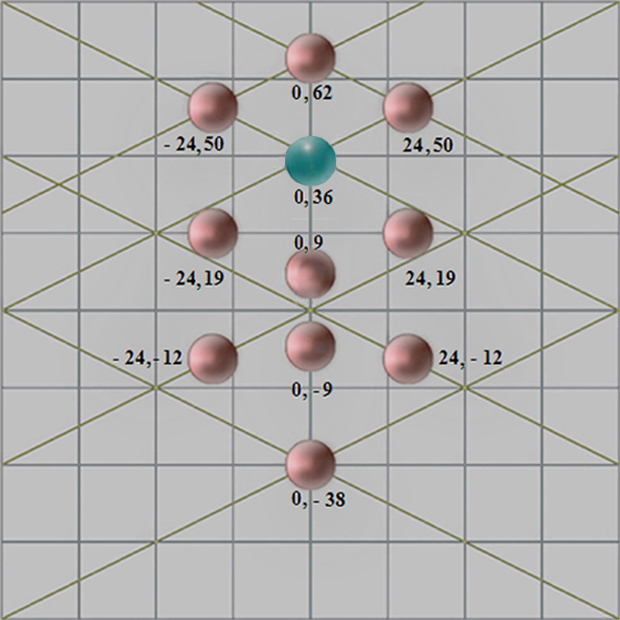
Detalles de la ilustración:
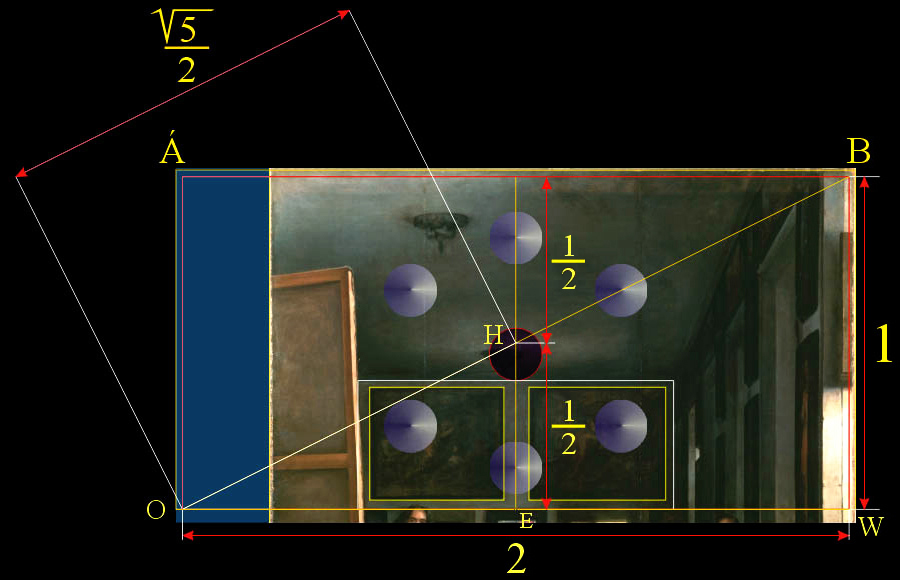
Dando el valor 2 al lado del cuadrado ÁBDC´ encontramos el modo de implicarnos en la proporción áurea.
La suma de los segmentos FH + HG = FG, igual al número áureo Φ.
En este análisis el centro de la Sefira número dos, Chokhmah, la Sabiduría, se halla en el itinerario del vector OB.
En el punto G descubrimos el uso práctico de tan sagrada proporción:
El vector IG discurre tangente al perímetro de la redondeada sobrefalda de la Infanta Margarita.
Desde la más remota antigüedad, de generación en generación, al Árbol de la Vida se le ha identificado con el Árbol del Conocimiento del jardín del Edén, en la creencia de representar el conocimiento secreto, que la literatura esotérica llama de los misterios.
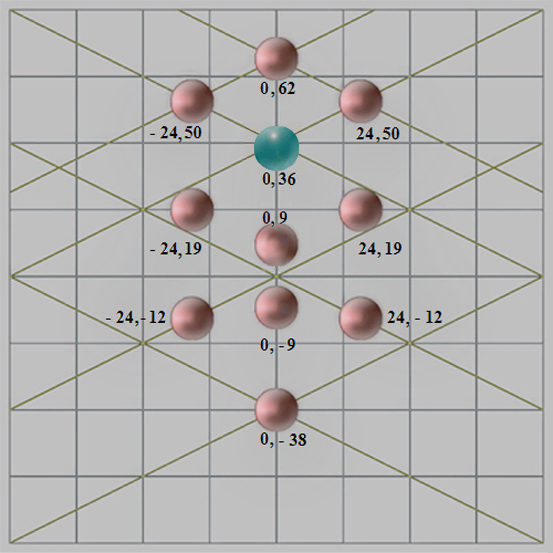
Hablamos, pues, de la causa oculta que anima al Árbol Sefirótico, un enigma que en Las Meninas tiene respuesta gracias a una cuadrícula de 152 unidades de lado, y equivalente a 3,141333... metros, con la que hemos asegurado la posición de las 10 + 1 esferas en coordenadas de números enteros.
 |
Numeración |
Hebreo |
Castellano |
Planeta |
Abscisas - X |
Ordenadas - Y |
|
I |
Kether |
Corona |
0 |
62 | ||
|
II |
Chokmah |
Sabiduría |
24 |
50 | ||
|
III |
Binah |
Inteligencia |
Saturno |
- 24 |
50 | |
|
Dahat |
Conocimiento |
0 |
36 | |||
|
IV |
Chesed |
Gracia |
Júpiter |
24 |
19 | |
|
V |
Geburah |
Fortaleza |
Marte |
- 24 |
19 | |
|
VI |
Tipheret |
Belleza |
Sol |
0 |
9 | |
|
VII |
Netzach |
Victoria |
Venus |
24 |
- 12 | |
|
VIII |
Hod |
Honor |
Mercurio |
- 24 |
- 12 | |
|
IX |
Yesod |
Fundamento |
Luna |
0 |
- 9 | |
|
X |
Malkhut |
Reino |
Tierra |
0 |
- 38 |
|
|
Este gráfico cartesiano confirma la estructura simbólica de Las Meninas, si bien, exhumamos una enseñanza sobrenatural tan sagrada como los dogmas de fe que la España de los Felipes impuso al nuevo mundo.
En el misticismo hebraico Chokmah, la Sabiduría, el grado más alto del conocimiento, que corresponde a la segunda Sefira del Árbol de la Vida, se la asocia con el lado derecho del cerebro que nos conecta con la percepción de lo intangible, la orientación espacial, la intuición o la creatividad, cuyo potencial más destacado es la actividad artística.
|
Numeración |
Hebreo |
Castellano |
Abscisa X |
Ordenada Y | |
|
II |
חכמה |
Chokmah |
Sabiduría |
24 |
50 |
Coordenada de la Sefira nº 2 Chokmah
|
2 חכמה Chochma, Sapientia, Filius. |
Secundum veſtimentum ſeu Sephira dicitur חכמה Chochma, Sapientia, cuius nomen eſt יה Iah; attribuitur ſecundæ in diuinis emanationi, ſcilicet Filio, ſicuti præcedens Patri, & ſequens Spiritui ſancto; ab Orpheo dicitur Cœlum, ab Homero Pallas nata ex cerebro Iouis. Canalis dicitur, cuius ope Deus influit ſupra Cherubinos, & ſupra firmamentum, hoc eſt, ſtellarum fixarum globum, ope Intelligentiæ quam רציאל Ratſiel vocant, mundique idealis inenarrabiles ſplendores exhibet; de quibus in ſequentibus fuſius. |
|
|
|
2 חכמה Chochma, Sabiduría, Hijo. |
La segunda vestidura de Dios es la Sefira denominada la Sabiduría, es decir; Chokmah, cuyo nombre es Yah; y se le atribuye a la segunda emanación divina, es decir, al Hijo, cuya anterior es el Padre y la posterior es el Espíritu Santo. Orfeo la llama Cielo, y según Homero Palas nació del cerebro de Júpiter. Se dice que es un canal por el cual Dios fluye sobre los Querubines & sobre el firmamento, es decir, sobre el grupo de las estrellas fijas, con la ayuda de la inteligencia que llaman Ratziel, mundo ideal que exhibe esplendores indescriptibles, de lo que hay más en lo que sigue. |
|
CLASSIS IV. CABALA HEBRÆRVM - CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI. Tomus Secundus. GYMNASIVM. ROMÆ - Anno M DC LIII. |
La emanación divina desciende, pues, a través de los senderos del Árbol Sagrado, y, perennemente, su actividad constante asciende por los senderos hacia la primera causa hacedora.
Una
vez establecida la coordenada cartesiana del centro
de la Sefira
Chokmah, que
representa el punto de encuentro entre Geometría y Kabala,
es ineludible acreditar con buenas razones la
trama
invisible de Las Meninas:
No hay nada en estas Esferas que no presuma ser percepción, emoción o un legado sagrado.
Según Loeffler [4]; las cuatro enseñanzas superpuestas, que corresponden a la identificación de un símbolo, mito o leyenda, son:
|
De hecho, el contenido de esta investigación no tendría ningún sentido práctico sin el apoyo de la filosofía cabalística hebrea, cuyos escritos y emblemas influyeron decisivamente en la cultura occidental, sin embargo, a cambio, ensombrecieron su crédito celeste.
Asumimos, pues, la interpretación que aporta la Kabala sobre estas esferas invisibles, tan radiantes como el resplandor del relámpago, que en la organizada estructura áurea de Las Meninas cumplen la voluntad de su creador para dirigir los mundos conocidos y desconocidos.
 |
|
|
Más allá de la Geometría, los diez Sefirot representan las distintas etapas de la creación divina, que se simboliza en nuestro mundo físico a través del Árbol Sagrado de la Vida, donde su luz primordial emana a partir del centro de la esfera superior Kether, la Corona, hacia los demás Sefirot.
 |
Tal y como se ha decantado la secreta inventiva del maestro Velázquez, Las Meninas están inspiradas, pues, en el libro de la Creación, Sefer Yetzirah [5], en cuya narrativa se percibe la gran influencia de la Geometría y Matemática entre otras artes liberales.
El alfabeto hebreo lo componen, pues, 22 letras consonantes, y, básicamente, cada letra combina dos aspectos; el significante, es decir, el sonido, como en cualquier lenguaje hablado, y un particular bagaje.
Una letra que equivale a un jeroglífico,
y de un valor numérico de acuerdo al lugar que ocupa en la serie.
|
|
|
|
Del Sefer Yetzirah examinaremos, pues, la palabra Sefer, ספר, que se traduce por LIBRO:
| Palabra | Tercera letra | Segunda letra | Primera letra |
| LIBRO | ר | פ | ס |
| Letras | resh | peh | samekh |
| Valor numérico | 200 | 80 | 60 |
| Múltiplo pitagórico | 200 = 40 × 5 | 80 = 20 × 4 | 60 = 20 × 3 |
Se observa, pues, que el valor numérico de las tres letras que completan la Gematría de la palabra Sefer son múltiplos de 3 - 4 - 5 respectivamente, es decir, estamos analizando un método de lectura basado en la asignación de un valor numérico concreto a cada una de las 22 letras del alfabeto hebreo, y, añadiríamos, que con la puntuación diacrítica de estas tres mismas letras obtendríamos más significados.
En el inicio del primer capítulo del Sefer Yetzirah se dan distintas designaciones a la misma etimología de este vocablo:
Y Él creó Su Universo con tres libros, סֵפֶרים, Seferim:
y, וסִפּוּר - Sipur, con comunicación.
Athanasius Kircher, en el año 1652, propone la siguiente traducción:
מספר ספר סופר id eſt, numerantem, numerum, & numeratum.
Recordaríamos, pues, que España, el país donde prosperó por siglos la Kabala, se la conoce por Sefarad, ספרד, un vocablo que también contiene la misma etimología que la palabra previamente analizada.
|
|
|
|
Hablamos, por lo tanto, de tres cifras concretas que tuvieron una gran utilidad en los cálculos de los constructores del antiguo Egipto:
|
Que si se toman tres reglas, una de tres pies, otra de cuatro y una tercera de cinco, y se las junta de modo que reunidos sus extremos de punta a punta formen un triángulo, se tendrá una escuadra perfecta. |
Escribe Vitrubio en el capítulo II del Libro Noveno de Los Diez Libros de Arquitectura [6]:
Pitágoras inventó una escuadra que no requiere el trabajo de los artesanos, (...).
|
|
|
Cuentan que Pitágoras halló la virtud de la potencia del triángulo rectángulo, con tanto contentamiento y satisfacción de haberle hallado, que en señal de la merced recibida ofrendó a la diosa Minerva el ritual Hecatombe en el cual sacrificó cien vacas.
ab2 + ac2 = bc2
Y esto nos enseña, pues, que las 22 letras hebreas no son signos convencionales, sino pictogramas de números naturales, ordenados e infinitos, otorgadas a la humanidad en épocas remotas para que con ellas se desvelasen los misterios de la creación.
(3) + (3 + 4) + (3 + 4 + 5) = 22
|
|
 |
 |
 |
|
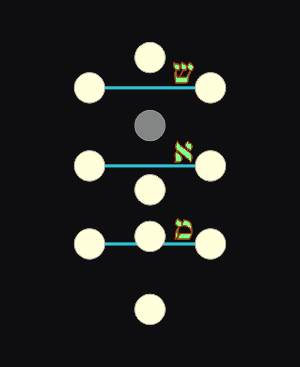
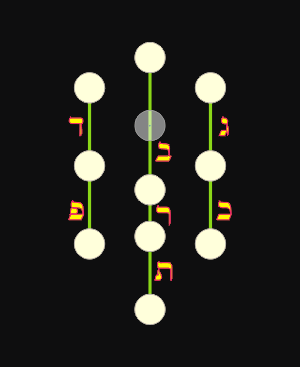
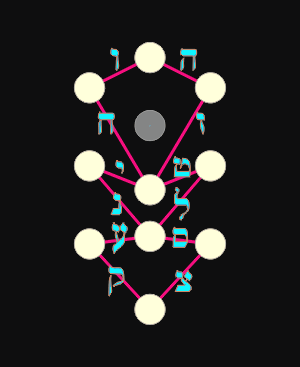
3 = (3) Senderos Horizontales - Letras madres |
7 = (3 + 4) Senderos Verticales - Letras dobles |
12 = (3 + 4 + 5) Senderos Diagonales - Letras simples |
|
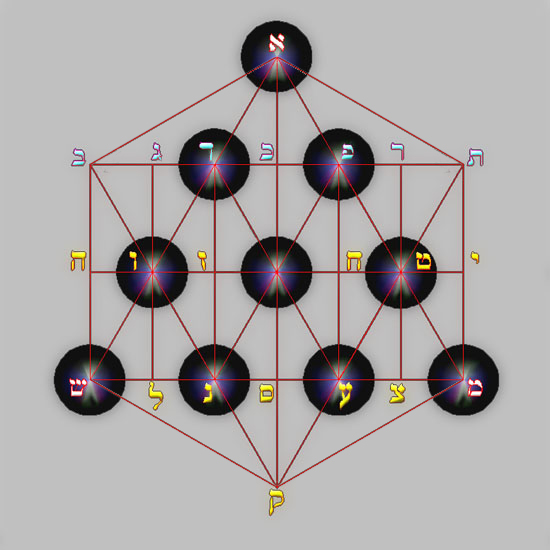
עשר ספירות בלי מה ועשרים ושתים אותיות יסוד שלש מאות ושבע כפולות ושתים עשרה פשוטות׃ |
Diez Sefirot en el vacío y veintidós letras de Fundamento: Tres Madres, Siete Dobles y Doce Simples. |
|
Sefer Yetzirah - 1:2 |
Pitagóricamente, pues, no se echa en falta ningún guarismo, porque es cierto que existe, además, una congruente conexión entre las 22 + 1 intersecciones de la geometría de la estrella de seis puntas, llamada la Estrella de David, y el triángulo equilátero que compone el Tetraktys pitagórico.
|
Estos son los Diez Sefirot de la nada: El aliento de Dios vivo, aliento del aliento, agua del aliento, fuego del agua. Arriba, abajo, sur, norte, este, oeste.
אלו עשר ספירות בלימה רוח אלהים חיים רוח מרוח מים מרוח אש ממים רום ותחת ודרום צפון מזרח ומערב |
 |
I |
Kether |
רוח אלהים חיים |
aliento de Dios vivo |
|
II |
Chokmah |
רוח מרוח |
aliento del aliento |
||
|
III |
Binah |
מים מרוח |
agua del aliento |
||
|
Dahat |
בלימה |
nada |
|||
|
IV |
Chesed |
אש ממים |
fuego del agua |
||
|
V |
Geburah |
רום |
arriba |
||
|
VI |
Tipheret |
ותחת |
abajo |
||
|
VII |
Netzach |
ודרום |
sur |
||
|
VIII |
Hod |
צפון |
norte |
||
|
IX |
Yesod |
מזרח |
este |
||
|
X |
Malkhut |
ומערב |
oeste |
|
|
1 + 2 + 3 + 4 = 10
|
|
Según el
Sefer Yetzirah, Yah,
יה, el Señor del
Mundo, el arquitecto del Universo, Omnipotente y Eterno, es el creador de los 32
senderos de Sabiduría del Árbol Sagrado de la Vida, que lo completan las 22
letras hebreas más los diez Sefirot.
 |
|
|
El libro de la Creación o Sefer Yetzirah, un libro oral de más de veinte siglos de antigüedad, se inicia del siguiente modo:
Con treinta y dos senderos prodigiosos de Sabiduría grabó Yah.
בשלשים ושתים נתיבות פליאות חכמה חקק יה
Sefer Yetzirah 1:1
|
|
Y se descubre en la primera frase del Sefer Yetzirah la importancia de cada pormenor, y de resaltar, pues, al número 32, el número 32 de la Matemática, de la Geometría y Aritmética, con el que operaremos en la división del perímetro del círculo.
De manera, que el tamaño de la unidad patrón que Diego Velázquez utilizó en la Geometría de Las Meninas depende de la división del perímetro de un Círculo en 320 partes:
|
360º ÷ 320 = 1,125º
Y su inverso:
1 ÷ 1,125º = 0,888888...º |
No obstante, estos guarismos son los mismos que los del resultado de la división del perímetro del Círculo entre 32 partes, pero de acuerdo con los datos del Problema 48 del Papiro de Ahmes de 1650 a. c.
Radio = 4,5 unidades,
valiendo Pi = 256/81 = 3,1605...
PERÍMETRO DEL CÍRCULO
|
|
2 × 3,1605... × 4,5 unidades = 28,444444... unidades
28,444444... unidades ÷ 32 = 0,888888... unidades
Y su inverso:
1 ÷ 0,888888... = 1,125
| 9 partes | Unidades | La Pulgada en 9 partes | Pulgadas | Milímetros | ||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 |
| 8/8 | = | 1 | 8/9 | = | 0,888888... | 20,666666... |
|
|
En resumen, para acomodar a los diez Sefirot en coordenadas de unidades enteras, como sucede en Las Meninas, donde además se utiliza el sistema castellano, una pulgada equivale a 1,125 unidades.
Sabemos, pues, que 1,125 unidades equivale a una pulgada castellana, y que la pulgada castellana se divide en doce partes iguales llamadas líneas, por lo que Diego Velázquez, en sus precisas mediciones, fracciona la pulgada castellana en 9 partes iguales para poder operar con la unidad.
8/9 de pulgada equivale a la unidad en este nuevo plano de Las Meninas.
|
9/9 |
8/9 |
7/9 |
6/9 |
5/9 |
4/9 |
3/9 |
2/9 |
1/9 |
|
1,125 |
1 |
0,875 |
0,75 |
0,625 |
0,5 |
0,375 |
0,25 |
0,125 |
| 180º | 160º | 140º | 120º | 100º | 80º | 60º | 40º | 20º |
|
12/12 |
11/12 |
10/12 |
9/12 |
8/12 |
7/12 |
6/12 |
5/12 |
4/12 |
3/12 |
2/12 |
1/12 |
|
1,125 |
1,03125 |
0,9375 |
0,84375 |
0,75 |
0,65625 |
0,5625 |
0,46875 |
0,375 |
0,28125 |
0,1875 |
0,09375 |
| 180º | 165º | 150º | 135º | 120º | 105º | 90º | 75º | 60º | 45º | 30º | 15º |
|
15/15 |
14/15 |
13/15 |
12/15 |
11/15 |
10/15 |
9/15 |
8/15 |
7/15 |
6/15 |
5/15 |
4/15 |
3/15 |
2/15 |
1/15 |
|
1,125 |
1,05 |
0,975 |
0,9 |
0,825 |
0,75 |
0,675 |
0,6 |
0,525 |
0,45 |
0,375 |
0,3 |
0,225 |
0,15 |
0,075 |
| 180º | 168º | 156º | 144º | 132º | 120º | 108º | 96º | 84º | 72º | 60º | 48º | 36º | 24º | 12º |
|
|
Estas tres tablas de divisores del número 1,125 representan, pues, 36 maneras posibles de operar con la pulgada castellana a partir de la apertura de ángulo de tres distintos polígonos regulares, que ofrecen, en los cálculos matemáticos, una absoluta precisión.
 |
||
|
Octodecágono - 18 lados |
Icositetrágono - 24 lados |
Triacontágono - 30 lados |
|
|
||||
| Pulgadas - Fracciones - Grados | ||||
|
Pulgadas (Fracción x/9) |
Pulgadas (Fracción x/12) |
Pulgadas (Fracción x/15) |
||
| Pulgadas | Milímetros | Unidades | ||
| Grados |
CONCLUSIÓN
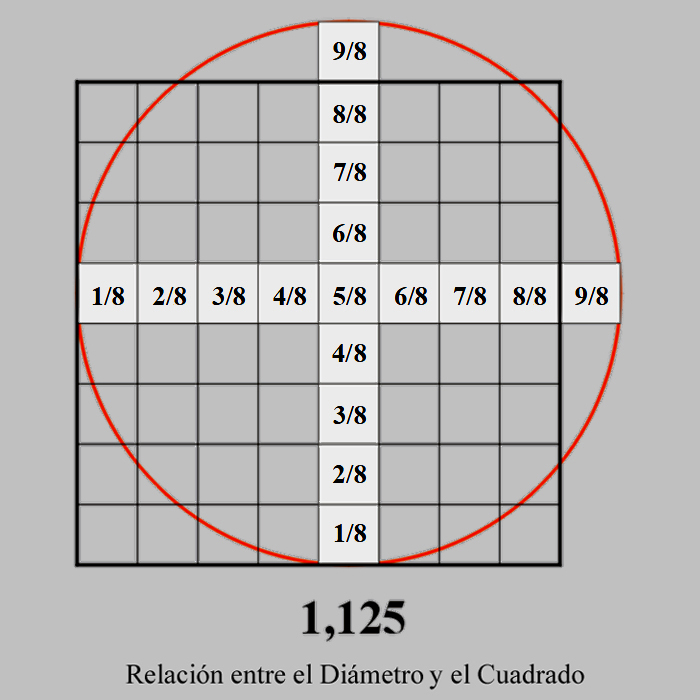
Al número 1,125 se le podría considerar el número patrón de todas las unidades longitudinales, ya que es una magnitud cuya función no ha variado desde la época de los Sumerios, y, además de ser el resultado de la proporción que cuadra el círculo con un Pi = 256/81, es también el común dividendo, como hemos ya analizado, de la pulgada fraccionada en: 9 - 12 - 15 partes en el sistema de medidas castellano.
 |
Y remontándonos al siglo XXVI a. c., el tamaño de la Pirámide de Kefrén y el número 1,125 se ponen de acuerdo a través de la terna pitagórica.
Veamos:
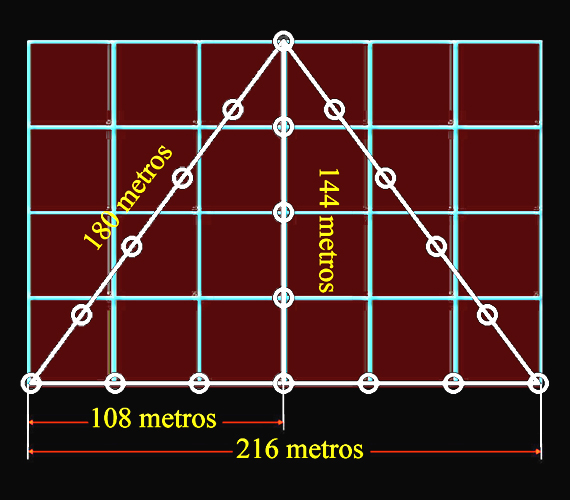 |
Terna pitagórica de la Pirámide de Kefrén en metros |
Y operando inversamente con el tamaño real de esta Pirámide egipcia rehabilitaríamos, con total garantía, a los tres guarismos de la terna pitagórica.
| 108 | ÷ |
32 |
= | 3,375 | ÷ | 1,125 | = | 3 |
| 144 | ÷ | = | 4,5 | ÷ | = | 4 | ||
|
180 |
÷ |
= |
5,625 |
÷ |
= |
5 |
Resultado que simplifica afrontar la Geometría de Las Meninas [7]:
|
Eſta ciencia tiene mas loa que las otras tres, comprehendidas en el numero de Matematicas; porque auiendo grandes contiendas entre las ſestas de caſi todas las diſciplinas, todos los geometras en toda parte concuerdan en vno, ni jamas ſobre la facultad ſe halla entre ellos algun debate, porque aunque diſputan de los puntos, de las lineas, y de las ſuperficies, ſi ſe pueden diuidir o no; en lo demas concuerdan, ni difieren en dotrina o preceptos; antes ſe esfuerçan para exceder el vno al otro, con nueuas y mas ſutiles inuenciones. |
Hablamos, pues, de una proporción sesquioctava, que es aquella que contiene la unidad y un octavo de ella:
|
8/8 + 1/8 = 9/8
1 + 1/8 = 1,125 |
Y eso pone de relieve que, en Música, al tono pitagórico le corresponde la proporción sesquioctava 9/8, que trata del ratio entre la quinta y la cuarta:
3/2 ÷ 4/3 = 9/8 = 1,125.
Queda probada, pues, la versatilidad del número 1,125, que representa un valor constante y de tipo permanente en el ejercicio de las cuatro artes liberales del quadrivium, o cuadrivio, es decir; el recurso necesario de cualquiera de las cuatro ciencias de la antigua Grecia y del mundo medieval basadas en un mismo patrón teórico; el número.
Aritmética, Geometría, Astronomía, o Astrología, y Música [8].
Tabla de frecuencias de afinación en la Escala pitagórica
|
Nota |
Intervalo |
Tono |
|
Origen numérico |
||
|
Do |
Unísono |
1 |
= |
1 |
= |
1/1 |
|
Re b |
Segunda menor |
1,05349794239 |
= |
28 / 35 |
= |
256/243 |
|
Do # |
Unísono aumentado |
1,06787109375 |
= |
37 / 211 |
= |
2187/2048 |
|
Re |
Segunda mayor |
1,125 |
= |
32 / 23 |
= |
9/8 |
|
Mi b |
Tercera menor |
1,18518518519 |
= |
25 / 33 |
= |
32/27 |
|
Re # |
Segunda aumentada |
1,20135498047 |
= |
39 / 214 |
= |
19683/16394 |
|
Mi |
Tercera mayor |
1,265625 |
= |
34 / 26 |
= |
81/64 |
|
Fa |
Cuarta justa |
1,33333333333 |
= |
22 / 3 |
= |
4/3 |
|
Sol b |
Quinta disminuida |
1,40466392318 |
= |
210 / 36 |
= |
1024/729 |
|
Fa # |
Cuarta aumentada |
1,423828125 |
= |
36 / 29 |
= |
729/512 |
|
Sol |
Quinta justa |
1,5 |
= |
3 / 2 |
= |
3/2 |
|
La b |
Sexta menor |
1,58024691358 |
= |
27 / 34 |
= |
128/81 |
|
Sol # |
Quinta aumentada |
1,60180664063 |
= |
38 / 212 |
= |
6561/4096 |
|
La |
Sexta mayor |
1,6875 |
= |
33 / 24 |
= |
27/16 |
|
Si b |
Séptima menor |
1,7777777777 |
= |
24 / 32 |
= |
16/9 |
|
La # |
Sexta aumentada |
1,8020324707 |
= |
310 / 215 |
= |
59049/32768 |
|
Si |
Séptima mayor |
1,8984375 |
= |
35 / 27 |
= |
243/128 |
|
Do |
Octava |
2 |
= |
2 |
= |
2 /1 |
Esta tabla prueba que el número 1,125 es la piedra angular de la armonía musical, cuyo valor corresponde a la proporción sesquioctava, 9/8, es decir; el tono pitagórico, el componente fundamental de la música occidental, además de apadrinar el sistema unificado de las medidas geométricas que Velázquez concibió en su obra maestra.
Este hallazgo eleva a Las Meninas a un nuevo nivel de genialidad, ya que el número 1,125 es el hilo conductor de la composición de esta obra, lo que convierte a esta pintura en una sinfonía visual regida por los mismos principios matemáticos que la música de las esferas.
El maestro Diego Velázquez al incorporar esta proporción no sólo demuestra un conocimiento profundo de las ciencias del quadrivium, y de las leyes que rigen a la Aritmética, la Geometría y la Música, sino la interconexión que convierte a este trabajo artístico en una sinfonía de líneas, formas y figuras de música visible, dispuestas según los mismos principios divinos que rigen el cosmos del Árbol de la Vida.
En 1637 René Descartes
publicaba, en
un apéndice al Discurso del Método,
los hallazgos de la
Geometría Analítica usando un
conjunto de ejes y coordenadas;
esta nueva Geometría facilitaba
representar las rectas, curvas y figuras geométricas mediante el valor numérico
de las expresiones algebraicas
[9].
Los diagramas de coordenadas cartesianas fueron a partir de René Descartes una de las herramientas más empleadas en el estudio de las Matemáticas.
 |
|
|
Al día de hoy, y dado que Las Meninas es una obra de arte pintada hace 365 años, se entiende, pues, la necesidad de documentar cualquier dato acerca de la envergadura de este óleo en medidas castellanas.
Para tal fin hemos operado con vectores de un grosor de una milésima de milímetro, 0,001 mm., y una certidumbre de una diezmilésima de unidad en los resultados que aportamos, es decir; de un margen de seguridad de 0,0001 de unidad.
Un margen prácticamente invisible al ojo humano.
 |
 |
|
|
Ahora bien, tengamos en cuenta que la cuadrícula de 152 unidades de lado es el límite geométrico que garantiza la posición de los llamados diez Sefirot en coordenadas de números enteros, aunque hay otras dos maneras más de extender el número de coordenadas de trabajo hasta el mismo borde del perímetro del lienzo de Las Meninas:
en base al tamaño de sus medidas originales y
de acuerdo con las medidas actuales.
En las siguientes tablas mostramos los resultados más viables de llevar a cabo por el pintor Diego Velázquez.
Caso Primero
|
Sistema de medidas |
Anchura |
|
Altura |
|
Coordenadas |
|
metros |
2,79 |
× |
3,2085 |
= |
8,951715 |
|
unidades |
135 |
× |
155,25 |
= |
20.958,75 |
|
pulgadas |
120 |
× |
138 |
= |
16.560 |
|
líneas |
1.440 |
× |
1.656 |
= |
21384.640 |
|
puntos |
17.280 |
× |
19.872 |
= |
3431388.160 |
|
|
De acuerdo a estas medidas, y utilizando un cronograma [10], responderíamos, pues, al significado del tamaño de las 1656 líneas de la altura de este lienzo, cantidad, que no sólo indicaría el año de esta obra, sino que, además, explicaría el probable título original de Las Meninas.
En Europa los cronogramas disfrutaron de su mayor apogeo entre los siglos XVI y XVIII, particularmente en los territorios del Sacro Imperio Romano y los Países Bajos, donde se usaron en inscripciones conmemorativas y material impreso.
La palabra cronograma, derivada del griego χρόνος, tiempo, y γράμμα, escritura, se la define como una frase memorable, normalmente en latín, cuya fecha viene dada por la suma total de las letras latinas que intervienen en una frase de acuerdo con el valor de los números romanos:
La faMILIa DeL sr Phe IIII
50 + 1000 + 1 + 50 + 1 + 500 + 50 + 1 + 1 + 1 + 1 = 1656
|
|
En 1734, después del incendio del Alcázar, esta obra de Velázquez se halla reseñada en la relación de las obras rescatadas del siguiente modo:
Otro sin Marco con Bastidor de quatro Vs de alto y tres vs y terzia de ancho de la familia del sr Phe quarto origl de Velazquez.
En esta descripción se cita a este lienzo como La familia del sr Phe quarto, aunque, más tarde, se le rebautizaría como La Familia [11].
Entendemos, pues, que todavía en el siglo XVIII el nombre original del lienzo de Las Meninas era:
La familia del sr Phe quarto.
El título original de Las Meninas depende, por tanto, del año 1656 y de cinco distintas variables:
La primera edad del Mundo abarca 1656 años, desde Adán hasta el Diluvio Universal según el Génesis, capítulo 5.
Sabemos que 1656 es el año en el que se elaboraron Las Meninas.
Dividiendo 1656 líneas castellanas entre 12 obtendríamos 138 pulgadas, que representa la altura original de Las Meninas.
Felipe IV y la reina Mariana celebraban en el año 1656 el séptimo aniversario de su matrimonio.
Y, finalmente, prevaleció el predicamento del rey Felipe IV en el título original de este óleo.
No obstante,
las medidas actuales de Las Meninas corresponden a:
133,6250 unidades por 153,9375 unidades.
Caso Segundo
|
Sistema de medidas |
Anchura |
Altura |
Coordenadas |
||
|
metros |
2,761583333 |
× |
3,181375 |
= |
8,785632... |
|
unidades |
133,6250 |
× |
153,9375 |
= |
20.569 y 115/128 |
|
pulgadas |
118 y 7/9 |
× |
136 y 10/12 |
= |
16.252 y 41/54 |
|
líneas |
1.425 y 4/12 |
× |
1.642 |
= |
21340.397 y 4/12 |
|
puntos |
17.104 |
× |
19.704 |
= |
3371017.216 |
|
|
Estas dos tablas de coordenadas perimetrales son anexas a la rejilla de trabajo de 152 unidades de lado; no obstante, estamos hablando de una abultada cantidad de coordenadas posibles, y, al mismo tiempo, de una manera práctica de ordenar la superficie de este lienzo.
Dicho de otro modo, en la posibilidad de fragmentar la superficie del lienzo de Las Meninas en tantas coordenadas como sea oportuno.
Hablamos, pues, de 3371017.216 puntos castellanos localizados sobre la superficie de este lienzo.
No dudamos, pues, de la exactitud de los siete Casos de medición que planteamos, ya que, además de estar unificado todo el cómputo geométrico y aritmético en tres sistemas diferentes de medición, es crucial señalar que todas las relaciones descriptivas de Las Meninas están trazadas en un único plano.
Aunque
el lienzo de Las Meninas
no tenga formato
cuadrado, sin embargo, planteamos el concepto del cuadrado como Geometría inicial, y el
consecuente estudio de su tamaño actual.
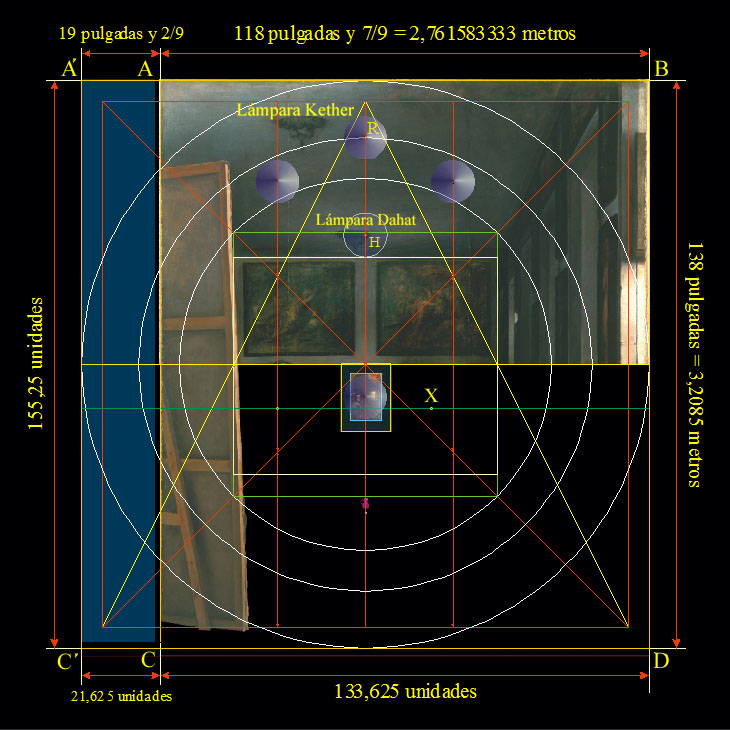
A continuación mostramos, pues, el formato cuadrado, y el análisis del tamaño de la anchura del lienzo de Las Meninas.
| Añadido junto al Bastidor | Anchura del lienzo | Total | |||
| unidades | 21,625 unidades | + | 133,625 unidades | = | 155,25 unidades |
| sistema castellano | 19 pulgadas y 2/9 | + | 118 pulgadas y 7/9 | = | 138 pulgadas |
| sistema métrico | 0,446916666 metros | + | 2,761583333 metros | = | 3,2085 metros |
|
|
 |
|
|
|
Hablamos, pues, de un cuadrado de 138 pulgadas de lado, que incluye todo el perímetro del lienzo de Las Meninas, que denominamos Borde del orillo del lino original, y de una cuadrícula de 152 unidades como soporte de las diez esferas cabalistas del Árbol de la Vida.
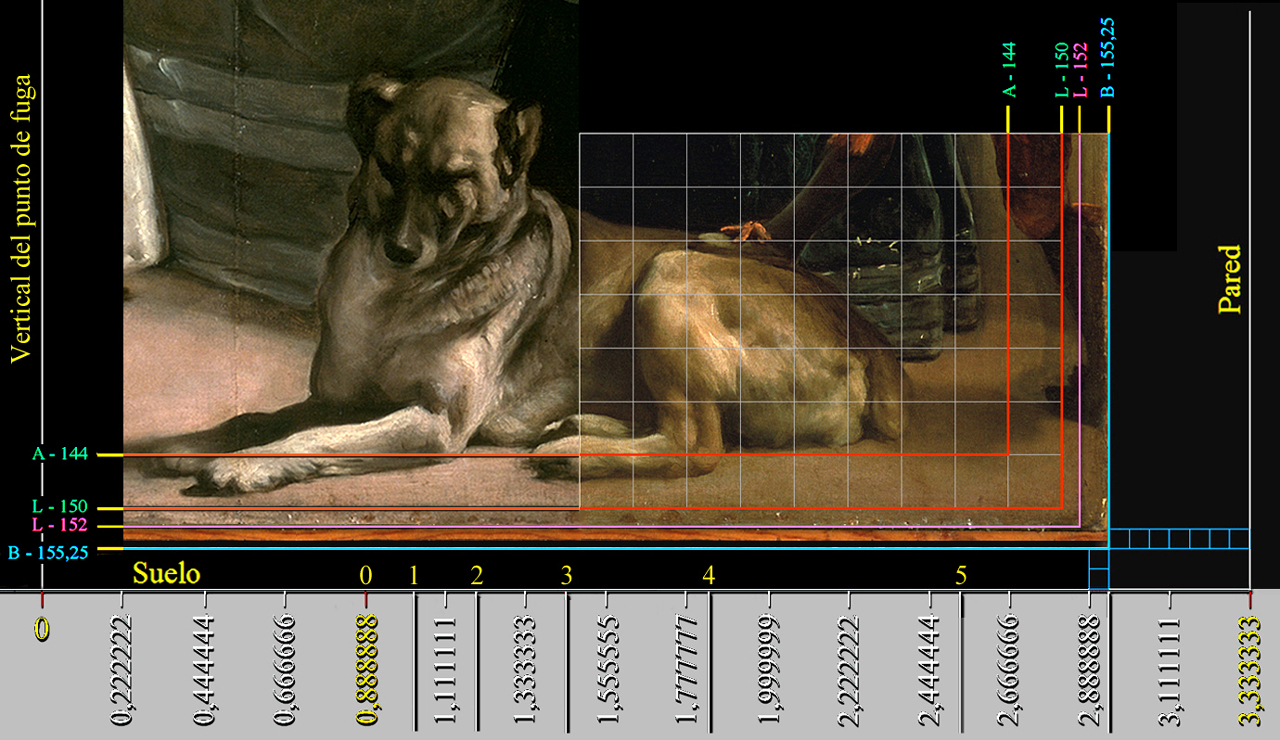
Tipos de cuadrículas sobre la superficie de Las Meninas:
 |
|
| Modelo |
Acotación geométrica |
Unidades |
Pulgadas |
Color del Punto |
Abscisa - X |
Ordenada - Y |
| A - 144 |
Línea de acotación |
144 × 144 |
128 × 128 |
Amarillo |
0 |
0 |
| L - 150 | Límite de la rejilla de 150 unidades | 150 × 150 | 133 y 1/3 × 133 y 1/3 | |||
| L - 152 | Límite de la rejilla de 152 unidades | 152 × 152 | 135 y 1/9 × 135 y 1/9 | |||
| B - 155,25 |
Borde del orillo del lino original |
155,25 × 155,25 |
138 × 138 |
Azul |
0 |
0,375 |
|
Pared del Fondo |
72 × 60 |
64 × 53 y 1/3 |
Amarillo |
0 |
0 |
|
0,375 unidades = 7,75 mm. |
 |
|
|
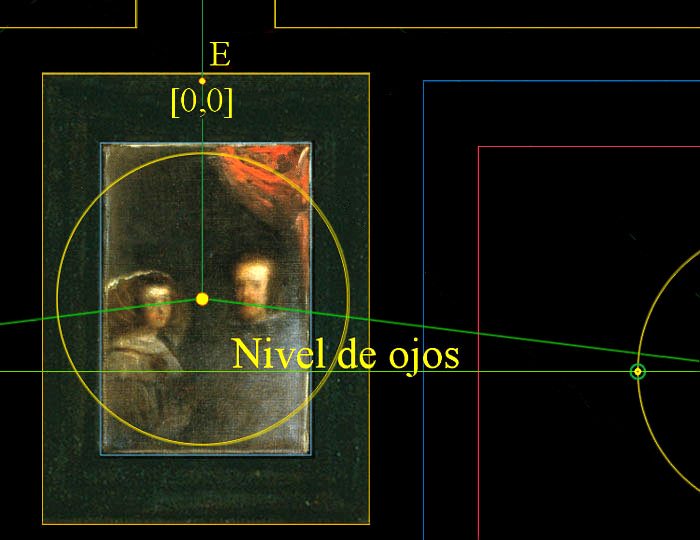
Estas cuatro herramientas geométricas cuadradas están sometidas al mismo sistema de medidas y coordenadas; ya que mantenemos como centro fijo en la cuadrícula de trabajo el punto E:
[0, 0].
Este centro se localiza en la parte superior del marco del espejo.
 |
|
|
Las coordenadas en unidades del centro del
Marco de madera del Espejo, y del Cristal del Espejo:
X
= 0,15 ; Y = - 9.
La sombra a lo largo del lateral izquierdo del
Marco de madera del Espejo acrecienta su anchura, pero no altera la posición de la Sefira nº 9, Yesod, El Fundamento:
X
= 0 ; Y = - 9.
Para mayor certeza, se comprueba, pues, que por las cuatro esquinas del marco del Espejo transitan a 54º las trayectorias de los dos vectores diagonales de su formato rectangular.
|
|
|
|
El centro del Espejo corresponde, al mismo tiempo, al centro de la Sefira nº 9, Yesod, El Fundamento, cuyo guarismo es el múltiplo dominante en el análisis del Espejo, e, igualmente, del año de la creación de Las Meninas en 1656.
1 + 6 + 5 + 6 = 18 ; 1 + 8 = 9
La rejilla de 152 unidades
La
base geométrica de esta investigación está sustentada por
la perfecta relación entre el antiguo sistema castellano y el actual sistema
métrico.
|
Sistema castellano |
vara |
pie |
palmo |
pulgada |
línea |
punto |
unidades |
milímetros |
|
vara |
1 |
3 |
4 |
36 |
432 |
5184 |
40,5 |
837 |
|
pie |
|
1 |
3/4 |
12 |
144 |
1728 |
13,5 |
279 |
|
palmo |
|
|
1 |
9 |
108 |
1296 |
10,125 |
209,25 |
|
pulgada |
|
|
|
1 |
12 |
144 |
1,125 |
23,25 |
|
línea |
|
|
|
|
1 |
12 |
0,09375 |
1,9375 |
|
punto |
|
|
|
|
|
1 |
0,0078125 |
0,16145833 |
|
|
|
|
||||||
| UNIDAD | PULGADA | MILÍMETRO |
El tamaño del lado de la rejilla de 152 unidades, que equivale en medidas castellanas a 3 varas, 2 pies, 3 pulgadas, 1 línea y 4 puntos, se desglosa, pues, a través del exacto nexo entre las unidades, las medidas castellanas y el sistema métrico.
|
Sistema castellano |
cantidades |
operación |
total en unidades |
operación | total en pulgadas |
operación |
total en metros |
||||||
|
varas |
3 |
3 × 40,5 |
= |
121,5 |
3 × 3 × 12 | = | 108 |
3 × 3 × 0,279 |
= |
2,511 |
|||
|
pies |
2 |
2 × 13,5 |
= |
27 |
2 × 12 | = | 24 |
2 × 0,279 |
= |
0,558 |
|||
|
pulgadas |
3 |
3 × 1,125 |
= |
3,375 |
3 × 1 | = | 3 |
3 × 0,279/12 |
= |
0,06975 |
|||
|
líneas |
1 |
1 × 0,09375 |
= |
0,09375 |
1 × 1/12 | = | 0,083333... |
1 × 0,279/12/12 |
= |
0,0019375 |
|||
|
puntos |
4 |
4 × 0,0078125 |
= |
0,03125 |
4 × 1/12/12 | = | 0,027777... |
4 × 0,279/12/12/12 |
= |
0,0006458333... |
|||
|
152 unidades |
135,111111...pulgadas |
3,141333... metros |
|
|
Sabemos, pues, que 1,125 unidades equivale a una pulgada castellana en la superficie del lienzo de Las Meninas.
| 36 partes | Unidades | La Pulgada de 12 líneas | Pulgadas | Milímetros | ||
| 36/32 | = | 1,125 | 12/12 | = | 1 | 23,25 |
| 33/32 | = | 1,03125 | 11/12 | = | 0,916666 | 21,3125 |
| 30/32 | = | 0,9375 | 10/12 | = | 0,833333 | 19,375 |
| 27/32 | = | 0,84375 | 9/12 | = | 0,75 | 17,4375 |
| 24/32 | = | 0,75 | 8/12 | = | 0,666666 | 15,5 |
| 21/32 | = | 0,65625 | 7/12 | = | 0,583333 | 13,5625 |
| 18/32 | = | 0,5625 | 6/12 | = | 0,5 | 11,625 |
| 15/32 | = | 0,46875 | 5/12 | = | 0,416666 | 9,6875 |
| 12/32 | = | 0,375 | 4/12 | = | 0,333333 | 7,75 |
| 9/32 | = | 0,28125 | 3/12 | = | 0,25 | 5,8125 |
| 6/32 | = | 0,1875 | 2/12 | = | 0,166666 | 3,875 |
| 3/32 | = | 0,09375 | 1/12 | = | 0,083333 | 1,9375 |
|
El Pie Real equivale a 12 pulgadas, y mide 0,279 metros |
El tamaño de la cuadrícula de 152 unidades en metros:
152 unidades / 1,125 unidades por pulgada = 135 pulgadas y 1/9.
135 pulgadas y 1/9 × 0,02325 metros por pulgada = 3,141333... metros.
Análisis:
Primero hagamos la siguiente operación aritmética para estar al corriente del valor en metros de una pulgada castellana:
Un pie Real de 0,279 metros / 12 = 0,02325 metros; este resultado equivale a una pulgada.
0,02325/9 = 0,002583333 metros, este resultado equivale a 1/9 de pulgada.
Ahora multiplicaremos y sumaremos adecuadamente:
135 pulgadas × 0,02325 metros por pulgada = 3,13875 metros,
más 0,002583333 metros, que es el valor de 1/9 de pulgada.
Conclusión:
3,13875 metros + 0,002583333 metros = 3,141333333 metros.
Este resultado representa la altura necesaria para acomodar la Geometría áurea sobre el lienzo de Las Meninas.
El espacio sagrado
En 1656 apremiaba en Palacio la designación de la heredera, y, como Aposentador Mayor, a Velázquez le
asistía el derecho de estar presente en esta ceremonia, en cuyo
autorretrato puso
en juego una gran carga simbólica [12].
|
Quando ſe jura Principe, pone la ſilla donde ſe ha de ſentar; y en los Reynos donde es jurado le toca por derecho. He viſto en la que fue jurado el Rey don Iayme de Aragon, y en ella fue jurado el Rey Filipe III. Otra preeminencia es tener llaue de toda la Casa Real, ſin que aya puerta que eſtè cerrada para el. Quando en Palacio ay maſcaras, comedias, torneos y ſaraos, conſulta con su Mageſtad el orden que ſe ha de guardar en todo. |
Y sin percibirse, en Las Meninas estaríamos contemplando, pues, la jura de la heredera al trono, una afirmación que podría estar respaldada, además, por los testigos presentes en esta ingeniosa partida de Ajedrez.
|
Los nombres de los ſcachos ſon ocho: y el mas principal ſe llama Rey, en cuyo bien, ò contraria fortuna conſiſte el ganarſe, ò perderſe el juego. El ſegundo ſe llama reyna, ò dama, ò dona en Ytaliano. Los que eſtan mas coniuntos a eſtas dos pieças ſe llaman Arfiles, vno arfil del rey, y otro arfil de la Reyna, ò dama. Tras eſtos ſe ponen otros, vno de vna parte, y otro de la otra: y llamanſe Cauallos: el que eſta de la parte del rey, ſe llama cauallo del rey: y el que eſta de la parte de la dama, ſe llama cauallo de la dama. Tras eſtos eſtan otros dos, vno de la parte del rey en la vltima caſa, y llamaſe Roque del Rey: y otro en la otra vltima caſa de la parte de la dama, y llamaſe Roque de la dama. En la ſegunda linea delante deſtas pieças eſtan otros ocho trebejos, que ſe llaman Peones, y cada vno ſe nombra peon de aquella pieça, delante de la qual eſta ſituado [13]. |
 |
|
|
Faltarían por acomodar en este tablero de Ajedrez a los dos bufones:
La bufona Maribárbola
y el bufón Nicolás Pertusato,
y, por supuesto, al perro situado en el primer plano.
Unos testigos que podrían ser peones, pero como afirma en 1561 Ruy López de Segura, reconocido como el primer campeón de ajedrez registrado en Europa, a la Infanta Margarita la consideraríamos, pues, peón de su padre el rey Felipe IV:
cada vno ſe nombra peon de aquella pieça, delante de la qual eſta ſituado.
 |
Y es exacto, que el Límite de la rejilla de 152 unidades equivale a una cuadrícula de 8 × 8 subcuadrados de 19 unidades de lado cada uno:
Hablamos, pues, de una gran cuadrícula de 64 subcuadrados, que vienen a ser el mismo número de casillas que componen el tablero del Ajedrez.
El cuadrado de ocho, 64, es la expresión de un todo perfecto.
Es plenitud, pero también el campo cerrado de una lucha, que se expresa en el tablero del ajedrez de sesenta y cuatro casillas.
La madre de Buda nació en una familia dotada de sesenta y cuatro clases de cualidades.
Confucio nació en la sesenta y cuatro generación desde Hoang-Ti, fundador de su dinastía.
Jesucristo, según San Lucas, habría nacido en la sesenta y cuatro generación desde Adán.
Sesenta y cuatro mulas arrastraron el carro fúnebre de Alejandro Magno.
Sesenta y cuatro personas llevaban los restos del emperador fallecido en China.
Sesenta y cuatro es el número simbólico del logro terrenal [14].
Habría que añadir, pues, que la rejilla de trabajo de 152 unidades, de 8 × 8 subcuadrados, hacen un total de 64 subcuadrados, una cantidad que se descompone en la suma de 36 más 28.
36 y 28 se relacionan, numéricamente, con el Sol y la Luna, ya que el año solar computado de este modo equivale a 360 días, es decir; diez veces 36, mientras que el año lunar se calcula con mayor precisión: 13 lunas de 28 días cada una, lo que hace un total de 364 días.
La discrepancia entre las cifras reseñadas y la duración real del año asciende a cinco días en un caso, y, en el otro, a uno, aunque estos días perdidos fueron utilizados como días festivos en honor al Sol o la Luna, y compensados por meses intercalados que corregían estas irregularidades.
 |
 |
|
64 Hexagramas Libro del I Ching |
Giordano Bruno - 1583 |
Pero aún hay más ejemplos.
El llamado pavimento mosaico asociado al número 64 conlleva cualidades extraordinarias, y se menciona en la Biblia, Éxodo 24:10, cuando fue revelado a Moisés y a los Setenta Ancianos en el Monte Sinaí [15].
La congregación de Israel recibió el mandato de Jehovah para emplearlo como patrón de medida en la construcción del Tabernáculo.
|
Y vieron al Dios de Israel; y había debajo de sus pies como un embaldosado de zafiro, semejante al cielo cuando está sereno.
ויראו את אלהי ישׂראל ותחת רגליו כמעשׂה לבנת הספיר וכעצם השׁמים לטהר׃
Éxodo 24:10 |
El pavimento mosaico asociado al número
64 reaviva, pues, a uno de los problemas más conocido de la Matemática; la cuadratura del círculo,
una demostración que consiste en construir un Cuadrado cuya área sea igual a
la de un Círculo.
 |
|
British Museum de Londres |
 |
|
|
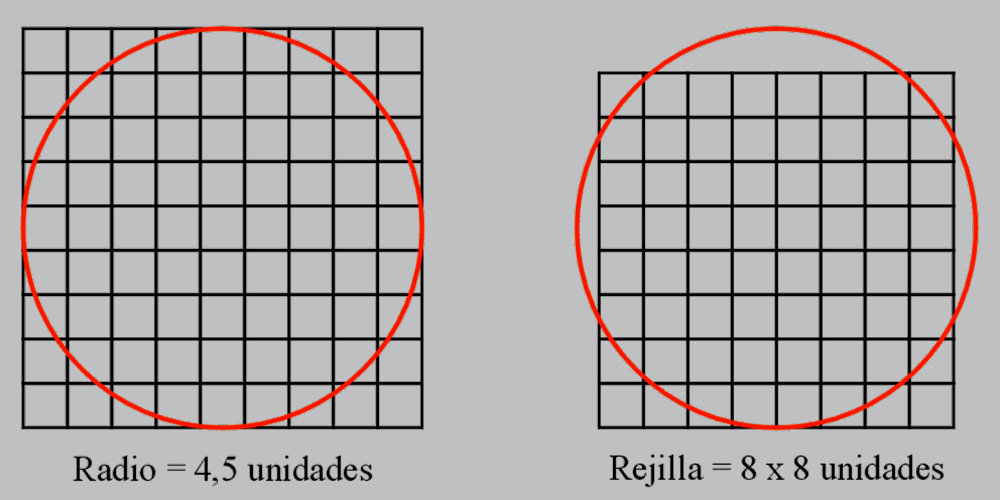
En las antiguas culturas de oriente para averiguar áreas circulares se empleaba un enfoque geométrico, y valga el ejemplo del Problema 48 del Papiro de Ahmes de 1650 a. c. que utiliza, para calcular el área del círculo, un diámetro igual al lado de 9 unidades del cuadrado circunscrito y un valor de Pi = 256/81 = 3,1605...
En Música, el valor de la fracción 256/81, que corresponde al decimal 3,1605..., representa el intervalo de una sexta menor compuesta en la escala pitagórica, es decir; este ratio es el resultado de multiplicar la sexta menor, 128/81, por una octava, 2/1.
|
Nota |
Intervalo |
Tono |
|
Origen numérico |
|
Geometría |
||
|
Do |
Unísono |
1 |
= |
1 |
= |
1/1 |
|
|
|
Re |
Segunda mayor |
1,125 |
= |
32 / 23 |
= |
9/8 |
||
|
La b |
Sexta menor |
1,58024691358 |
= |
27 / 34 |
= |
128/81 |
||
|
Do |
Octava |
2 |
= |
2 |
= |
2 /1 |
||
|
La b |
Sexta menor compuesta |
3,16049382716 |
= |
28 / 34 |
= |
256/81 |
= |
Pi de Ahmes |
Calculemos, pues, el área de un círculo con un valor de Pi = 256/81 = 3,1605..., y un diámetro de 9 unidades igual al lado del cuadrado circunscrito:
|
OPERACIÓN
π × 4,52
3,1605... × 4,5 × 4,5 = 64 unidades cuadradas |
El escriba tebano Ahmes llega a la resolución del problema de manera exacta, sin embargo, con el valor de Pi = 22/7 de Arquímedes el área sería:
π × 4,52 = 63,64285... unidades cuadradas.
Este valor se aproxima con un 99,44...% de exactitud a un cuadrado de lado 8, es decir; 8 × 8 = 64 unidades cuadradas.
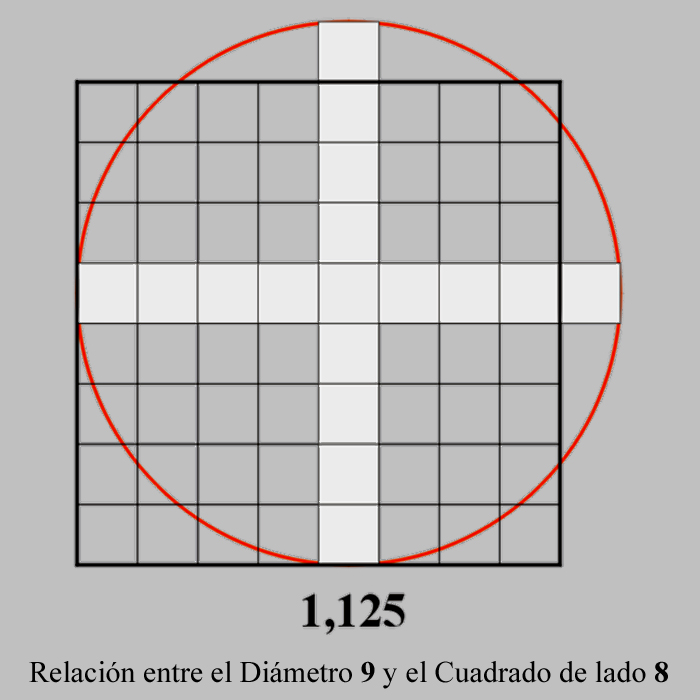 |
El Papiro de Ahmes de 1650 a. c. viene a darnos la razón, porque es el origen e hilo conductor del relato de todas las medidas geométricas que analizamos, ya que la demostración de la cuadratura del círculo que este papiro plantea se basa en una proporción sesquioctava, es decir; se trata de una proporción que contiene la unidad y un octavo de ella:
|
8/8 + 1/8 = 9/8
1 + 1/8 = 1,125 |
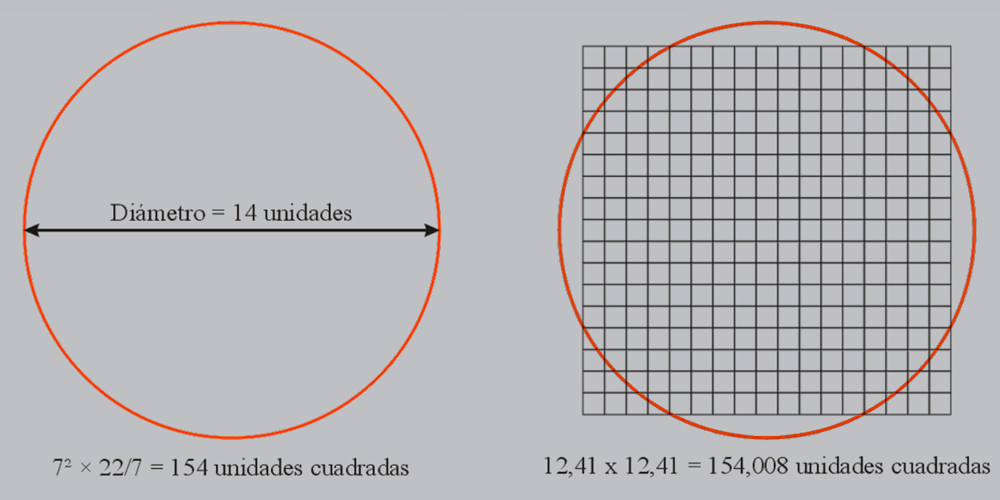
Entretanto, en el año 1050, Franco de Lieja propone en el tratado De quadratura circuli, una aproximación del 100,005... %, a este mismo problema de las matemáticas griegas.
 |
|
|
De manera, que con regla, compás y un Pi racionalizado por Arquímedes, Pi = 22/7 = 3,142857142..., esta relación del radio de un círculo con su circunferencia no tuvo una solución exacta durante siglos, por lo que cuadrar el círculo al 100 % se convirtió en sinónimo de una tarea sin solución.
Aunque podríamos agregar, que para un científico de la época de Velázquez era una cuestión superada, porque un + 0,005... % de error a causa del valor de Pi racionalizado era tan intranscendente que no se tenía en cuenta.
|
El perímetro de la circunferencia valor 97 y 3/7 ≈ 97,428571...
El valor del diámetro es 31
Entonces Pi ≈ 97,428571... / 31 ≈ 3,142857142... ≈ 3 y 1/7 = 22/7 |
 |
|
|
Tenemos preparado, pues, todos los números necesarios para resolver con el 98,214... % de exactitud la Cuadratura del Círculo en Las Meninas.
RESOLUCIÓN:
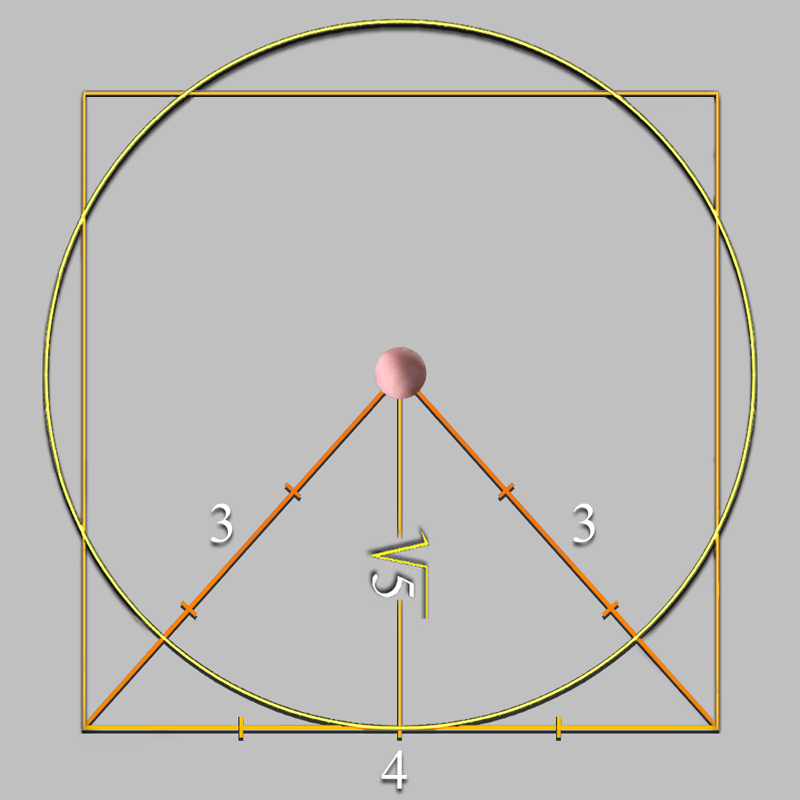
Si a 76 unidades le corresponde 2 en la cuadrícula de trabajo, y la Sefira nº 6, Tiferet, La Belleza, se sitúa en la coordenada [0, 9], entonces su centro estará situado a 76 + 9 = 85 unidades del borde inferior, y le correspondería, por tanto, el radio del círculo de valor X:
X = 85 × 2 ÷ 76 = 2,236... ≈ √5, que es el resultado que buscamos.
 |
|
|
|
Área del Cuadrado; 4 × 4 = 16 unidades cuadradas
Área del Círculo; π × (√5)2 ≈ 15,714285... unidades cuadradas |
 |
|
98,214... % |
Lo que resulta, que la exactitud concreta de la Cuadratura del Círculo de Las Meninas es del 98,214285...% usando el Pi de Arquímedes de 22/7.
|
CONSTANTE DE PI |
FRACCIÓN |
RADIO |
ÁREA DEL CÍRCULO | ÁREA DEL CUADRADO |
PRECISIÓN |
||
|
Pi actual |
π | × |
(√5)^2 |
= | 5π = 15,707963... | 4 × 4 |
98,174769...% |
| Zu Chongzhi | 355/113 | × | (√5)^2 | = | 15,707964... | 4 × 4 | 98,174779...% |
|
Velázquez |
1178/375 | × |
(√5)^2 |
= | 15,706666... | 4 × 4 | 98,166666...% |
|
Arquímedes |
22/7 | × |
(√5)^2 |
= | 15,714285... | 4 × 4 |
98,214285...% |
| Franco de Lieja | 22/7 | × |
(7)^2 |
= | 154 | 12,41 × 12,41 | 100,005194...% |
|
Ahmes |
256/81 | × |
(4,5)^2 |
= | 64 | 8 × 8 |
100% |
|
|
Y subrayaríamos que el centro geométrico de la Cuadratura del Círculo de Las Meninas no es un punto cualquiera, sino que su exacta ubicación coincide con el centro de la Sefira nº 6, Tiferet, la Belleza, conocida como el Corazón del Árbol de la Vida, fuente de toda Armonía y Belleza.
Ante estos datos, habría que tener bien presente además la evolución del valor de la constante Pi; desde su cálculo más remoto, de, al menos, 36 siglos de antigüedad, hasta su valor numérico exacto actual.
|
CONSTANTE DE PI |
VALOR NUMÉRICO |
FRACCIÓN | DESVIACIÓN |
ORIGEN HISTÓRICO |
|
Pi actual |
3,141592654... |
π | 0 |
Valor actual |
| Zu Chongzhi | 3,141592920... | 355/113 | 0,000000266... | Siglo V |
|
Velázquez |
3,141333333... |
1178/375 | 0,000259321... |
Codificado en Las Meninas |
|
Arquímedes |
3,142857142... |
22/7 | 0,001264489... |
Utilizado en el Siglo XVII |
|
Ahmes |
3,160493827... |
256/81 | 0,018901173... |
Papiro de Ahmes |
|
|
Esta tabla confirma, pues, que, el cálculo del número Pi, codificado por Velázquez, se acerca al valor actual de Pi, pero con una precisión superior a cualquier otra aproximación racional histórica conocida en España en el siglo XVII.
El código maestro del pintor español resuelve el problema con la máxima armonía, revindicando, pues, con su armoniosa Cuadratura del Círculo, tema de debate desde el Renacimiento hasta el siglo XVIII, el arte de la Pintura como una disciplina que pudiera rivalizar con la Filosofía y la Teología en la búsqueda de la verdad.
Y es, por tanto, esta aproximación a Pi la clave que posibilita hablar de la Cuadratura del Círculo en Las Meninas.
La fracción 1178/375 se justifica utilizando la pulgada castellana como base de medida.
La definición racional de la constante Pi es el resultado de la relación entre el perímetro y el diámetro de un círculo.
1178 es el valor del perímetro y 375 es del valor del diámetro.
|
|
|
|
La justificación fundamental es que el numerador de Velázquez, 1178, se descompone exactamente en los módulos geométricos validados en la pulgada castellana de su tiempo:
1178 = 2 × 19 × 31
19 - Corresponde, pues, al tamaño en unidades del lado de un subcuadrado de la rejilla de trabajo de 152 unidades.
31- Es el tamaño histórico del diámetro del círculo en la Geometría de Arquímedes de Pi = 22/7.
Y 375 del denominador corresponde al resultado de multiplicar el valor de la unidad de 1,125, que equivale a una pulgada, por 333,333333...
Y se demuestra, pues, que Velázquez no solo construyó su obra con precisión matemática, sino que su objetivo era reflejar el orden cósmico en su lienzo al establecer el centro de esta Cuadratura en un punto concreto que simbolizara la fuente de toda Armonía.
No obstante, cuando hablamos de Cuadrar el Círculo nos referimos, pues, a la exacta Geometría del óleo de Las Meninas, que como ejemplo se documenta en la previsible posición del pincel que sujeta Velázquez en su mano derecha.
 |
|
|
Dante Alighieri, 1265-1321, en el Canto XXXIII del Paraíso de la Divina Comedia daba por imposible la Cuadratura del Círculo:
|
Qual é il geométra che tutto s' affige Per misurar lo cerchio, e non ritrova, Pensando, quel principio ond' egli indige; Tale era lo a quella vista nuova: Veder volea, come si convenne L'imago al cerchio, e come vi s' indova; Ma non eran da ció le proprie penne; Se non che la mia mente fu percossa Da un fulgore, in che sua voglia venne. All´alta fantasia qui mancó possa: Ma giá volgeva il mio disiro e il velle, Si come ruota che igualmente é mossa, L' Amor che muove il Sole e l' altre stelle. |
|
Y como el geómetra que se concentra en medir el círculo, y no encuentra, en su pensamiento el principio que necesita, tal estaba yo con aquella nueva visión. Quería ver cómo la imagen se adaptaba al círculo, y cómo el círculo encajaba allí; pero mis propias fuerzas no estaban para ello salvo que mi mente fue iluminada por un resplandor que dejó satisfecha su deseo. Aquí perdí el sublime vigor de mi fantasía; mas mi anhelo y mi voluntad, ya giraban, como una rueda que se mueve de igual manera que el Amor que anima al Sol y las demás estrellas. |
|
|
El Canto XXXIII del Paraíso es el punto álgido de la culminación de un viaje espiritual, y transmite la metáfora perfecta de Dante, frustrado por el problema irresoluble de la cuadratura del círculo, lo compara con lo limitado de su mente para comprender la esencia de Dios.
En el estudio del Árbol de la Vida de Las Meninas
se advierte de su autor la calidad de un arquitecto científico, y, desde
su faceta de pintor,
propone un velado mensaje tras los efectos de la luz, que, con la ayuda de la
apropiada ciencia, ahora ya se conoce la función original de ciertos detalles pictóricos esenciales.
| Marco del Espejo | Pulgadas | Milímetros | Unidades | Unidades por pulgada | Pulgadas reales | |||
| Altura | 16 y 8/15 | 384,4 | 18,6 | ÷ | 0,3 | = | 62 | |
| Anchura | 12 | 279 | 13,5 | ÷ | 0,3 | = | 45 |
|
|
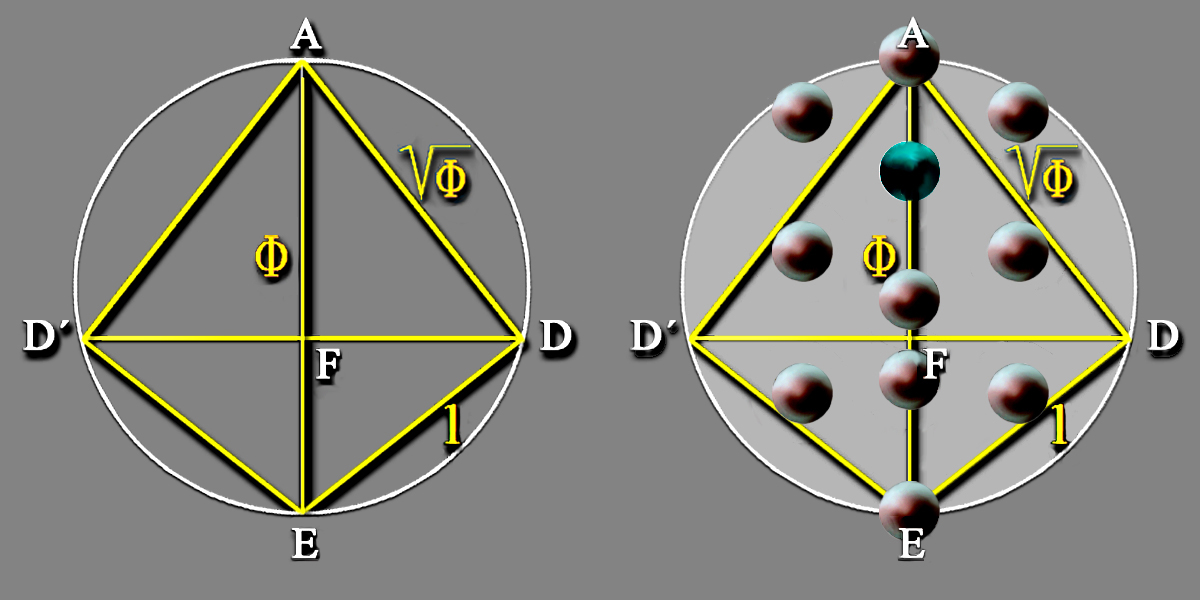
El ánimo geométrico velazqueño se adivina, pues, si construimos un decágono regular inscrito en un círculo con centro en el Espejo de una unidad de lado, en el que las cuatro esquinas de su marco se acomodarían en cuatro de sus diez vértices, y donde el radio mediría el número áureo Phi;
Φ = 1,618033...
|
|
|
√(2 + Φ) = √(2 + 1,618033...) = 1,902113... |
|
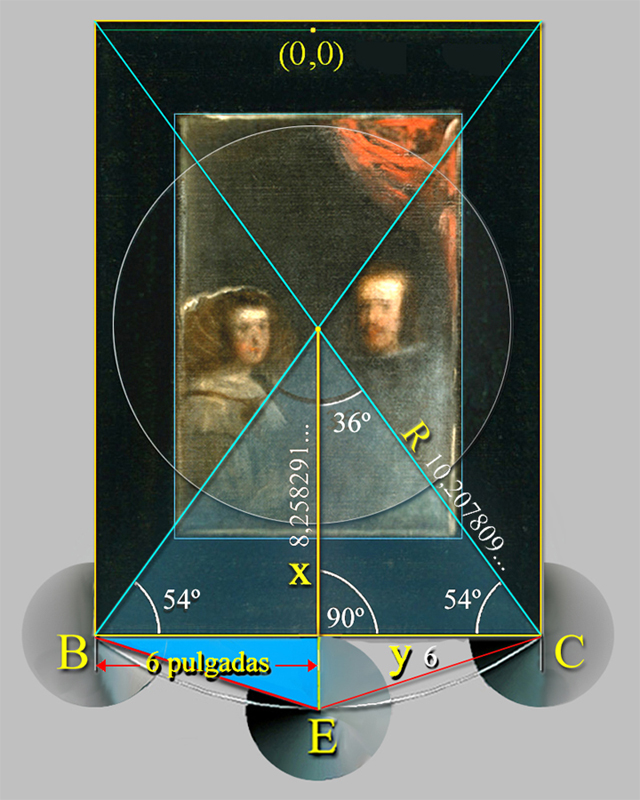
El tamaño del lado del pentágono regular, BC, inscrito en un círculo de radio, R, de valor Φ, se calcula con la fórmula de los polígonos regulares:
BC = 2R × seno(π/n)
Donde:
Y sustituyendo, la fórmula se convierte en:
BC = 2Φ × seno(π/5)
π/5 en radianes equivalen a 36º, y el seno de 36º = 0,587785..., por lo que el tamaño del lado del pentágono sería:
BC = 2Φ × 0,587785... = 1,902113... |
En un decágono regular el radio DB del círculo de valor Φ que lo circunscribe está en relación áurea con el lado de una unidad, por ejemplo BE.
DB/BE = Φ/1
Velázquez propone esta relación matemática al utilizar un pentágono de lado 6,308774... veces mayor, de manera, que sus cálculos dependieron del número áureo en la anchura exacta de 12 pulgadas del marco del Espejo.
|
|
6,308774... veces mayor corresponde, pues, al tamaño BE del lado de 6,308776... pulgadas del decágono que circunscribe al Espejo de Las Meninas.
En la siguiente imagen se muestra la concepción del Espejo en el área geométrica de una quinta parte de un pentágono regular, cuyo lado BC de 12 pulgadas corresponde al tamaño de la anchura del marco del Espejo de Las Meninas.
 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2R |
DIÁMETRO DEL PENTÁGONO |
= | 2 × 10,207809... pulgadas | ≈ | 20,415618... pulgadas | ≈ | 12 Φ + 1 |
2R ≈ 20,415618... pulgadas
12 Φ +1 ≈ 20,416407... pulgadas
|
TOLERANCIA |
0,000888638 unidades | ≈ | 0,0007899 pulgadas | ≈ | 0,018365175 milímetros |
EL ESPEJO & LA GEOMETRÍA SAGRADA
|
Diámetro del Pentágono:
Diámetro del Espejo:
Diagonal Pitagórica:
La expresión 12 Φ + 1:
|
Estos cuatro resultados tienen una tolerancia común, imperceptible al ojo humano, de un tercio de milímetro.
| Elemento | Fórmula | p |
pulgadas | milímetros | |||
| Diagonal Pitagórica | √(16,533223...² + 12²) | ≈ | 20,429172... | 0 | 0 | ||
| Expresión Phi | 12 Φ + 1 | ≈ | 20,416407... | - 0,012765... | - 0,296786... | ||
| Diámetro del Espejo | 12 / sin(π/5) | ≈ | 20,415849... | - 0,013323... | - 0,309759... | ||
| Diagonal del Espejo | 2 × R | ≈ | 20,415618... | - 0,013554... | - 0,315130... | ||
| Diagonal Phi |
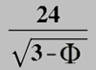 |
≈ | 20,415618... | - 0,013554... | - 0,315130... |
|
|
Y esto demuestra que la calculada gestación de esta obra maestra estuvo condicionada desde su inicio por la posición geométrica de las esferas cabalísticas, ya que fueron concebidas a priori para dar significado a ciertos detalles del escenario de esta pintura, y responden, pues, a una deliberada reivindicación del poder sacro, que, más allá de su etérea apreciación, invita a descubrir la personalidad menos conocida del maestro Velázquez.
Como huella de identidad, Velázquez, genio indiscutible de
la pintura española, y su amplia gama de soluciones técnicas e icnográficas
desveladas, suman, pues, para reconocer que poco se sabía de su talento
matemático, pero sí más de su gusto exquisito en la elección de los temas
pictóricos actualmente conocidos.
Y continuando con este análisis, Athanasius Kircher, sacerdote jesuita, políglota, erudito, estudioso orientalista, de espíritu enciclopédico y uno de los científicos más importante del siglo XVII, amplía en latín los siguientes contenidos de la Sefira nº 6, Tiferet, concebida justo encima del Espejo:
|
6 תפאר Tiphereth, Pulchritudo.
|
Sexta Sephirah ſeu veſtimentum Dei תפארת Tiphereth dicitur, cuis nomen יהוה Iehoua; Attributa eius ſunt ſpeculatio illuminans, lignum vitæ, voluptas, linea media, linea viridis, ambiens vniuerſum, lex ſcripta, Sacerdos magnus, ortus ſolis, ſpecies purpurea, ſeptuaginta duæ nationes in terra, ſigillum eius אמת אדני ; myſterium que eius in tertia litera tetragrammati, homo ſupremus ſiue Adam Cœleſtis, arbor in medio Paradiſi plantata. Per hanc Deus influit in ordinem virtutum, & hinc per Intelligentiam Raphael in Sphœram ſolis. Cauſa eſt omnis harmoniæ & pulchritudinis, quam in vniuerſso intuemur. |
|
|
|
|
|
|
|
6 תפאר Tiferet, Belleza.
|
La sexta vestidura de Dios es la Sefira denominada la Belleza, Tiferet, cuyo nombre es יהוה, Jehovah. Sus atributos son la especulación iluminadora, el árbol de la vida, el placer, la línea media, la línea verde que rodea al mundo, la ley escrita, el gran sacerdote, la salida del Sol, las especies púrpuras, las setenta y dos naciones de la tierra, su sello es la verdad de Adán; el misterio que se halla en la tercera letra del Tetragramaton, el hombre supremo y Adán del Cielo, árbol plantado en medio del Paraíso. A través de Tiferet Dios fluye en el orden de las virtudes, y, por lo tanto, a través de la Inteligencia Rafael en la esfera del Sol. Es la causa de toda la armonía y belleza que contemplamos en el mundo. |
|
CLASSIS IV. CABALA HEBRÆRVM - CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI. Tomus Secundus. GYMNASIVM. ROMÆ - Anno M DC LIII. |
En la Sefira nº 6, Tiferet, La Belleza, que se sitúa en la pared del fondo encima del espejo, es donde la presencia divina, o Shekinah, שכינה, se manifiesta, y alude, pues, al lugar exclusivo de la morada de Dios en el Templo de Jerusalén.
Tiferet salvaguarda el Corazón del Árbol, y, según la Kabala, es la causa de toda la armonía y belleza que contemplamos en el mundo.
Cauſa eſt omnis harmoniæ & pulchritudinis, quam in vniuerſso intuemur.
|
|
|
|
Hemos dado al tamaño del lado de la rejilla de 152 unidades el valor proporcional de 4.
O sea, que 152 unidades es el tamaño del lado de la cuadrícula, por lo que medio lado de esta cuadrícula valdría: 152 ÷ 2 = 76 unidades, de lo que se deduce; que si la Sefira nº 6, Tiferet, La Belleza, se sitúa en la coordenada [0, 9], entonces, su centro estaría situado a 85 unidades del borde inferior de esta rejilla es decir; una distancia equivalente al tamaño de la √5 = 2,236.
|
RESOLUCIÓN
Si a 76 unidades le corresponde 2 en la cuadrícula,
entonces a 85 unidades le corresponderá X:
X = 85 × 2 ÷ 76 = 2,236... ≈ √5, que es el resultado que buscamos |
La característica más notable de la Sefira nº 6, Tiferet, es su nombre divino Tetragrámaton, יהוה, y, como Corazón del Árbol, se interpreta como centro, núcleo y corazón del Ser asociado a la Jerusalén Celeste.
|
|
|
|
Y si medimos a partir del borde superior de la cuadrícula se comprueba, pues, que la Sefira nº 9, Yesod, El Fundamento, en la coordenada [0,- 9] en el centro del Espejo, también tiene estas mismas propiedades áureas.
Y se confirma, pues, la utilidad de esta resucitada Geometría, de manera, que las esferas cabalísticas quedan perfectamente alineadas de acuerdo a los vectores diagonales trazados sobre Las Meninas.
 |
|
|
La raíz cuadrada de 5, cuyo resultado corresponde a 2,236... con una exactitud de casi el 100 %, aparece en la fórmula del número áureo, y corresponde al tamaño de la hipotenusa de un triángulo rectángulo cuyos catetos miden 1 y 2 respectivamente.
|
|
|
|
Betzalel, בְּצַלְאֵל, fue designado por Moisés, מֹשֶׁה,
arquitecto del Tabernáculo
itinerante durante la estancia del pueblo hebreo en el desierto, aunque fue el
rey Salomón quien mandó construir en el templo de Jerusalén un Tabernáculo
permanente.
Examinaremos, pues, el nombre de Betzalel, בְּצַלְאֵל:
 |
 |
 |
 |
 |
||||||
| 30 | + | 1 | + | 30 | + | 90 | + | 2 | = | 153 |
|
|
El número 153 corresponde, pues, a la Gematría del nombre del arquitecto Betzalel, lo que indica que su propio nombre es su sello protector, ya que esta cantidad es también la medida exacta del lado de una rejilla perfecta de 9 x 9, es decir una cuadrícula conocida como el Sello de la Luna.
Veamos:
153 ÷ 9 = 17, o sea, que 17 unidades es el tamaño del lado de cada subcuadrado de una rejilla de 9 × 9, lo que hace un total de 81 subcuadrados.
|
|
|
Los números asociados con la Luna son 9, 81, 369 y 3321
Cada fila, columna y diagonal suma 369, y todos los números de este cuadrado suman un total de 3321 |
En el Árbol de la Vida, la Luna se aloja, pues, en la Sefira nº 9, y en el calendario hebreo este planeta es el que regula el tiempo desde la creación del mundo.
La Luna nueva de cualquier mes en particular depende de la primera Luna nueva del año cero hebreo, que, como es sabido, se gestó el 7 de Octubre de 3761 antes de Cristo de acorde con el Calendario Juliano.
Comenta el jesuita Kircher [16]:
|
Se llamaban sellos de los dioses, o lo que es lo mismo, alcázar de las siete estrellas errantes, por el hecho de que bajo ellas, según una determinada presunción de dominio, estaba la administración de todas las cosas. Consideraban que esto no se podía llevar a cabo sin que hicieran valer una fuerza misteriosa para atraer a dichos genios y ponerlos de su parte. |
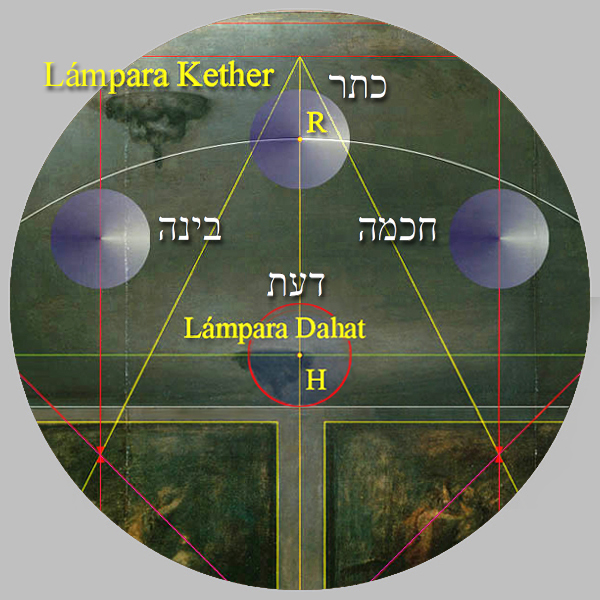
Añadiríamos, que es el propio Jehovah quien da nombre a las tres Sefirot superiores + Dahat, cuando, al hablar de las capacidades de Betzalel, le dice a Moisés:
Le he llenado del espíritu de Dios, con Sabiduría, con Entendimiento y con Conocimiento en toda clase de ingenio.
ואמלא אתו רוח אלהים בחכמה ובתבונה ובדעת ובכל־מלאכה׃
Éxodo 31:3
El reconocimiento divino del talento de Betzalel se perpetuó, pues, en los nombres de los Sefirot superiores del Árbol Sagrado de la Vida.
| Sefira |
Transliteración |
Hebreo |
Castellano |
| I | Kether - Ruach Elohim | רוח אלהים - כתר | Corona - Espíritu de Dios |
| II | Chokhmah | חכמה | Sabiduría |
| III | Binah | בינה | Entendimiento |
| no Sefira | Dahat | דעת | Conocimiento |
|
|
 |
|
|
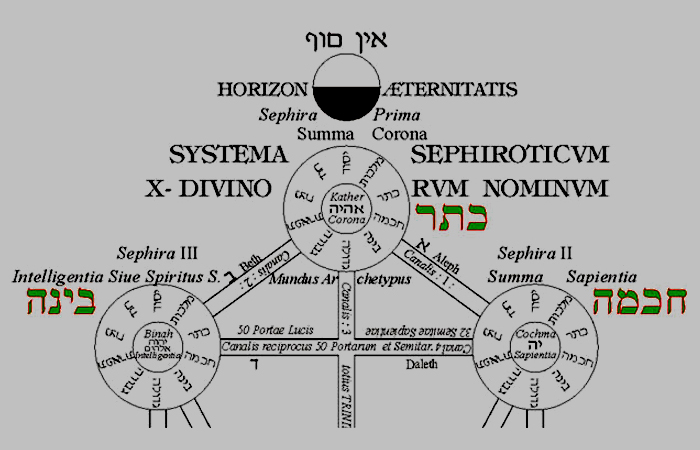
Athanasius Kircher, en su libro dedicado al emperador Fernando III, el padre de Mariana de Austria, es decir; el suegro, cuñado y primo del rey Felipe IV, describe, pues, esta zona del Árbol de la Vida del siguiente modo:
|
Hinc in arbore Sephiroth apud Cabaliſtas גמדות ſeu tres proprietates Deo affinguntur, quibus Deum omnia feciſſe memorant, ſuntque; בִּינָה חָכְמָה כֶּתֶר Corona, Sapientia, Intelligentia; quas R. Abraham in Iethſira appellat; מספר ספר סופר id eſt, numerantem, numerum, & numeratum; quae tria exacte reſpondent tribus ſupra a Iamblicho citatis nominibus, Amun, Phtha, Emepht. |
 |
|
De ahí, que entre los Cabalistas, גמדות, hay tres propiedades del árbol de los Sephiroth que se atribuyen a Dios, y con las que se recuerda que Dios hizo todas las cosas, y estas son; בִּינָה חָכְמָה כֶּתֶר, Corona, Sabiduría, Inteligencia, que R. Abraham en Jethſira llama; מספר ספר סופר, es decir; el numerador, el número y lo numerado, los cuales corresponden exactamente a los tres nombres citados anteriormente por Jámblico, Amón, Phtha, Emefht. |
Y para completar este asunto, añadiríamos, pues, que en el caso de Las Meninas, sin embargo, la rejilla de trabajo más apropiada es la de 152 unidades de lado, ya que sí cumple con las exigencias geométricas y simbólicas requeridas en esta obra de Diego Velázquez.
Veamos:
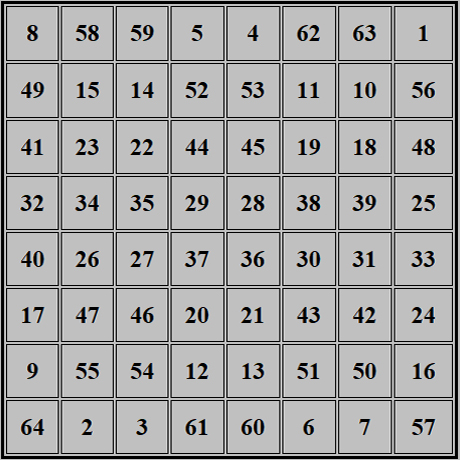
152 ÷ 8 = 19, o sea, que este tamaño de 19 unidades trata de una rejilla de 8 × 8, lo que hace un total de 64 subcuadrados.
 |
|
Los números asociados con Mercurio son 8, 64, 260 y 2080
Cada fila, columna y diagonal suma 260, y todos los números de este cuadrado suman un total de 2080 |
El Calendario Judío es lunisolar, y se basa en el ciclo Metónico descubierto por el astrónomo griego Metón, de tal modo que cada 19 años las mismas fechas del año quedan sincronizadas con las mismas fases de la Luna.
En consecuencia, y con el provecho de lo hasta ahora analizado, se prueba, pues, que el número sesenta y cuatro es el guarismo más importante del método que Velázquez afronta porque resuelve, al completo:
La relación entre el procedimiento geométrico y el cálculo numérico,
la posición exacta de las diez esferas del Árbol Sagrado,
una rejilla de 64 subcuadrados determina el límite geométrico de Las Meninas
y en la cuadrícula de trabajo se cuadra el círculo en un 98,214... %
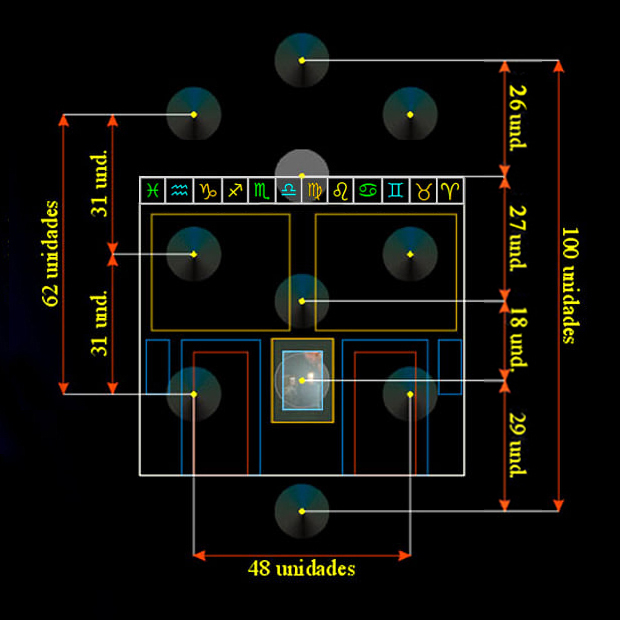
Planteamos, pues, un espacio pictórico en el que están anidados cuatro distintos escenarios, en cuyo centro se hallan retratados los monarcas en el Espejo en la Sefira nº 9, Yesod - El Fundamento.
 |
 |
|
|
| Anchura | escala | unidades | pulgadas | metros | ||
|
|
Habitación del Príncipe | 1/1 | 270 | 240 | 5,580 | |
|
|
Lienzo de Las Meninas | 1/2 | 135 | 120 | 2,79 | |
|
|
Pared del fondo | 1/3,75 | 72 | 64 | 1,488 | |
|
|
El Espejo | 1/20 | 13,5 | 12 | 0,279 |
Y, como hemos ya mostrado, las diez esferas del Árbol de la Vida están instaladas sobre una rejilla cuadrada de sesenta y cuatro subcuadrados, que constituye, pues, el soporte geométrico del árbol cabalístico que Velázquez propone.
En conclusión, la anchura de la pared del fondo de 64 pulgadas de este óleo preserva, pues, el poder y equilibrio del Árbol Sagrado de la Vida.
|
|
|
|
En este lienzo se gestó, pues, un acuerdo, por el que el rey Felipe IV ennoblecía a Diego Velázquez a cambio de que realizara, de manera segura, un trabajo cabalístico.
Un trámite acertado que distingue a Velázquez de los demás pintores de su época.
Una vez expuestas las ayudas necesarias, consultaremos, pues, en el libro de Joanne Stephano Rittangelio, 1606 - 1652, editado en Ámsterdam en 1642, la causa de la resuelta decisión velazqueña de plasmar la sublimación del Arte de la Magia Operativa con el beneplácito de la Kabala judía [17].
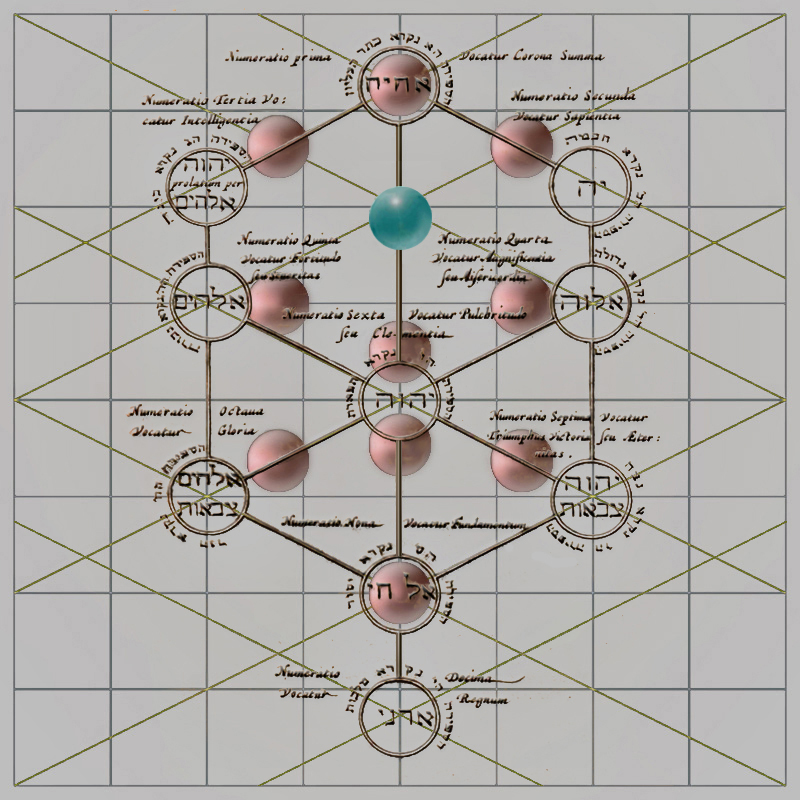
En definitiva, como resultado de la buena planificación, mostramos, pues, la imagen del germen de esta obra velazqueña confrontado con las normas geométricas que regían la actividad cabalística en el siglo XVII, y que en el libro de Joanne Stephano Rittangelio se consideran idóneas.
 |
Numeración |
Castellano |
Velázquez |
Rittangelio |
|
I |
Corona |
0, 62 |
0, 62 | |
|
II |
Sabiduría |
24, 50 |
38, 43 | |
|
III |
Inteligencia |
- 24, 50 |
- 38, 43 | |
|
Conocimiento |
0, 36 |
|||
|
IV |
Gracia |
24, 19 |
38, 19 | |
|
V |
Fortaleza |
- 24, 19 |
- 38, 19 | |
|
VI |
Belleza |
0, 9 |
0, 0 | |
|
VII |
Victoria |
24, - 12 |
38, - 19 | |
|
VIII |
Honor |
- 24, - 12 |
- 38, - 19 | |
|
IX |
Fundamento |
0, - 9 |
0, - 38 | |
|
X |
Reino |
0, - 38 |
0, - 62 |
|
&
El Árbol de Diego Velázquez. Madrid. 1656 |
Sin impedimento alguno se demuestra, pues, que ambas geometrías superpuestas coinciden debidamente en la cuadrícula de 152 unidades, lo que hace viable, además, considerar el cálculo del aire de una Sefira velazqueña.
|
|
Y, ante tanta evidencia, no podemos ocultar nuestro asombro, porque quien hubiera concebido el pequeño grabado del libro de Joanne Stephano Rittangelio no era español, sin embargo, es de destacar las siguientes características;
de una cuadrícula de 8 × 8 subcuadrados surgió el Árbol Sagrado de Joanne Stephano Rittangelio,
se comprueba, pues, que es perfectamente mesurable en unidades,
todos los centros de las diez esferas de Rittangelio se sitúan en coordenadas de números enteros de un total de 23104 coordenadas posibles,
estas diez esferas están instaladas en el mismo trazado geométrico que los vectores diagonales sobre Las Meninas
y, además, Velázquez, que opera en medidas castellanas, configura su Árbol de la Vida a partir de este pequeño grabado.
Esta imagen confirma, pues, la fuente de inspiración de la estructura del Árbol de la Vida del óleo de Las Meninas;
de Geometría,
de sistema de medidas en unidades
y de simbología.
El Tamaño de la Sefira
A estas esferas se las pueden medir físicamente a través
de la
división de la pared del fondo en doce partes iguales, ya que, si la
anchura de la pared del fondo pintada en Las Meninas mide 72
unidades, que corresponden a 72 unidades / 1,125 unidades por pulgada, que es
igual a 64 pulgadas, entonces, el tamaño del radio de
la esfera cabalista equivaldrá, pues, a la división de 64
pulgadas entre doce, que es igual a:
64 pulgadas / 12 = 5,333333... pulgadas.
O sea, que el tamaño del radio de la esfera cabalista mide, exactamente, la décima parte de la altura de la pared del fondo de 60 unidades, que equivale, pues, a 53,333333... pulgadas.
Por lo tanto, el diámetro de la Sefira medirá 5,333333... pulgadas por 2, que es igual a 10,666666... pulgadas.
|
|
|
|
Y 10,666666... pulgadas por 1,125 unidades por pulgada, que es igual a 12 unidades, corresponden, por tanto, al diámetro de la Sefira en unidades.
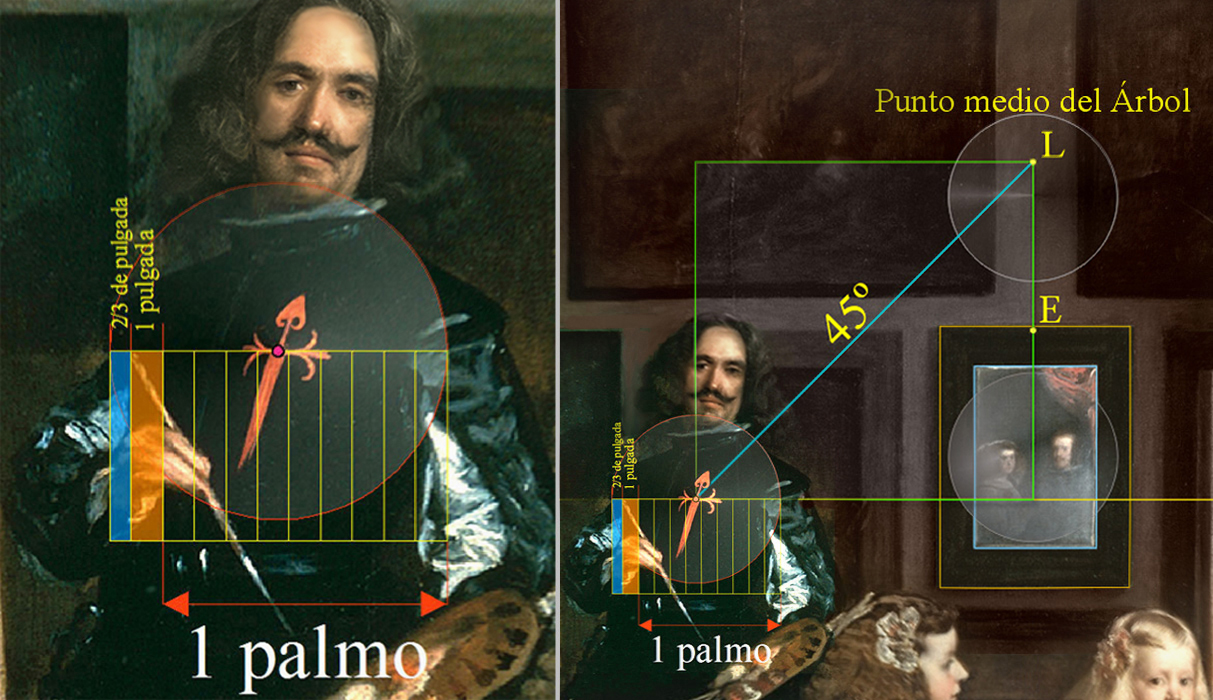
No obstante, al diámetro de 12 unidades de la Sefira, que corresponden a 10,666666... pulgadas en el lienzo de Las Meninas, se desglosa del siguiente modo:
1 palmo, que equivale a 9 pulgadas,
más 1 pulgada
y más 2/3 de pulgada.
 |
|
|
Consideraremos esta imagen como un episodio velazqueño inconfesable, aunque, a su vez, se revela el Corazón, y punto medio, del sacro símbolo con la ayuda de un vector inclinado a 45º, lo cual explica, pues, que el pintor, dependiendo de sí mismo, reivindicó su verdad atrincherado en el etéreo peso de su consciencia, y, de hecho, con exactitud reseñó la intención de su propósito.
Como hemos ilustrado, la Geometría superpuesta al lienzo de Las Meninas se inspira en un grabado del Sefer Yetzirah de Joanne Stephano Rittangelio, editado en Ámsterdam en 1642, una hipótesis que se demuestra comparando dos dibujos originales, pero de desigual formato:
Los 10 Sefirot + 1 en la cuadrícula de 152 unidades,
y el grabado del Árbol de Rittangelio.
Y tenemos, que si un dibujo se puede comparar a otro aplicando los mismos estándares de medición, hablaríamos, pues, de dos dibujos similares que sólo difieren en el tamaño.
En esencia, Velázquez no solo tomó la idea prestada del Árbol de la Vida de Rittangelio, sino que el diagrama del libro de Rittangelio ya estaba construido siguiendo principios métricos o geométricos fundamentales idénticos a los que el pintor español codificó en Las Meninas usando, pues, el sistema de LA UNIDAD, ya que ambos comparten el mismo lenguaje geométrico.
Verificaremos, de nuevo, el tamaño de la Sefira cabalística respecto a la cuadrícula de 152 unidades, y, a continuación, cotejaremos la hechura de nuestro modelo con el que se considera su mejor ejemplo en el libro de Joanne Stephano Rittangelio.
 |
|
|
La específica relación, entre el tamaño de la Sefira de Rittangelio y la de Velázquez, es de 4/3; un ratio que demuestra que la estructura general de ambas Geometrías, las posiciones puntuales de los Sefirot y la magnitud de la esferas cabalísticas guardan una proporcionalidad exacta.
Mostramos, pues, una demostración clara de cómo este análisis revela consistencias numéricas y proporcionales profundas que vinculan las esferas cabalística de la pintura de Velázquez con las del libro de Rittangelio.
Continuemos explorando.
En la pensada posición de la cruceta de la Cruz del Hábito de Santiago estaría instalado, pues, un eficaz conjuro en el pecho del pintor, que ratificaría, desde el leb, לב, corazón, el conocimiento cabalístico del maestro Velázquez.
La palabra hebrea leb alude a los treinta y dos senderos de Sabiduría del Árbol de la Vida, y el número 32 se compone de las siguientes letras:
| letra hebrea | grafía | valor numérico |
| Lamed |
 |
30 |
| Bet |
 |
2 |
Es decir; לב se lee leb, y se traduce por corazón, pero, lo que es más importante; son la última y primera letra de la Torah, por lo que dicha palabra encierra la totalidad de la revelación escrita desde el principio de Israel:
En el principio... Israel.
Bereshit... Israel.
 |
De lo personal, afortunadamente, ahora ya sabemos algo más del artista, y otro tema sería indagar en la hidalguía y limpieza de su sangre, que ante la falta de nobleza tuvo que bregar con el linaje familiar, pero, que gracias a la dispensa del papa Alejandro VII, y la firme resolución de Felipe IV, la consiguió.
Veamos, en Las Meninas Velázquez, desde la octava esfera Hod, conocida como el Honor, y celebrada, además, como la esfera soberana de la magia, estableció la alianza entre la firmeza de su corazón y el mundo de los Sefirot, y, con fe absoluta, reclamó el objeto de su deseo en el plano material.
La palabra Hod, הוד, significa Honor o Majestad, y se usa en el tratamiento de Su Majestad o Su Excelencia.
 |
Octauum veſtimentum Dei ſeu Sephirah eſt הוד Hod, id eſt, laus, honor, gloria. Nomen eius eſt אלהים צבאות Elohim Tſebaoth; attributa eius, myſterium columnæ, ac pedis ſiniſtri, hinc trahitur ſerpens antiquus, diſciplina Domini, Ramus, Cherub, Aharon, filij regis, molæ molentes. Eſt que Canalis, per quem Deus influit in Archangelos, & per Intelligentiam Michælem in Cœlum Mercurij; Cauſa & origo animalium eſt.
La octava vestidura de Dios es la Sefira denominada el Honor, Alabanza, Gloria, es decir; Hod, cuyo nombre es אלהים צבאות, Elohim Tſebaoth. Sus atributos son: El misterio de la columna, y el pie izquierdo, de aquí surge la antigua serpiente, la disciplina del Señor, rama, querubín, Aarón, hijo del rey, muelas de molino. Este es el canal por el cual Dios fluye hacia los Arcángeles, y, a través de la Inteligencia Miguel, hacia el Cielo de Mercurio. Es la causa y el origen de los animales.
Página 294 CLASSIS IV. CABALA HEBRÆRVM - CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI. Tomus Secundus. GYMNASIVM. ROMÆ - Anno M DC LIII |
Ante esta conclusión, destacaríamos, pues, la premura que acompaña a este atributo cabalístico sobre el corazón del pintor, que anticipó el lugar exacto del anhelado sueño de nobleza aún no hecho realidad.
De esta manera se explica, de una vez por todas, al único responsable de situar a la Cruz de Santiago con cualidad presagiada, que no casual, en su sitio.
La Cuadrícula del Marco del Espejo
En Matemática el número más pequeño con seis divisores es el
12: 1, 2, 3, 4, 6 y 12.
El número 12 y sus múltiplos son los únicos números que dividen exactamente en mitad, tercio, cuarto, dos tercios y tres cuartos a la anchura del Marco de madera del Espejo; de tal modo, que además de ser el objeto más protagonista de esta pintura, es en donde el pintor Velázquez propone la regia medida del Pie Real.
|
|
|
|
La anchura del Marco del Espejo mide 13,5 unidades
Factorización de 3 × 3 × 3 × 5 = 135.
Los divisores del número 135 son 8:
1, 3, 5, 9, 15, 27, 45, 135.
135 ÷ 1,125 = 120; que es lo que mide en pulgadas el ancho original del lienzo de Las Meninas.
La altura del Marco del Espejo mide 18,6 unidades
Factorización de 2 × 3 × 31 = 186.
Los divisores del número 186 son 8:
1, 2, 3, 6, 31, 62, 93, 186.
186 ÷ 8 = 23,25; que es la cantidad que equivale en milímetros una pulgada castellana.
| LA ALTURA | FUNDAMENTO | LA ANCHURA | ||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 0,3844 | 16 y 8/15 | 18,6 | = | 18,6 × 1 | 13,5 × 1 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 9,3 × 2 | 4,5 × 3 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 6,2 × 3 | 2,7 × 5 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 3,1 × 6 | 1,5 × 9 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,6 × 31 | 0,9 × 15 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,3 × 62 | 0,5 × 27 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,2 × 93 | 0,3 × 45 | = | 13,5 | 12 | 0,279 | |
| 0,3844 | 16 y 8/15 | 18,6 | = | 0,1 × 186 | 0,1 × 135 | = | 13,5 | 12 | 0,279 | |
|
|
| Marco del Espejo | Metros | Pulgadas | Unidades | Unidades por pulgada | Pulgadas reales | |||
| Altura | 0,3844 | 16 y 8/15 | 18,6 | ÷ | 0,3 | = | 62 | |
| Anchura | 0,279 | 12 | 13,5 | ÷ | 0,3 | = | 45 |
|
|
|
|
|
|
El Pie Real, el legítimo patrón de medidas castellano, ejerce el control absoluto sobre las medidas de este lienzo, y quedó puntualmente representado, sin duda, en la misma anchura del Marco del Espejo, ya que esta misma anchura equivale al lado de 12 pulgadas de un Pentágono regular.
Ofrecemos, pues, las dimensiones del Pie Real en unidades, pulgadas y su tamaño en la rejilla de trabajo.
| Unidades | Pulgadas | Cuadraditos |
| 13,5 | 12 | 4,5 |
En el siguiente paso verificaremos, pues, la altura del Marco del Espejo de Las Meninas, que mide 16,5333333.. pulgadas.
|
|
|
|
La fórmula de la tangente de un ángulo agudo, A, en un triángulo rectángulo es igual al cateto opuesto al ángulo analizado, y, dividido por el cateto contiguo, x, y, despejando, tenemos que el cateto contiguo, x, que trata del tamaño de la Apotema que buscamos, es igual al cateto adyacente, y, de 6 pulgadas, dividido por la tangente de 36º.
La tangente de 36º es aproximadamente igual a 0,726542...
y la altura del Marco del Espejo de Las Meninas corresponde, pues, a dos Apotemas, es decir; 8,258291... × 2 = 16,516583...pulgadas.
|
|
Las 16,5333333.. pulgadas de la altura del Marco del Espejo, que equivalen a 384,4 milĺimetros, tienen un exceso de 0,3894375 parte de un milímetro, es decir; una tolerancia del 0,1%.
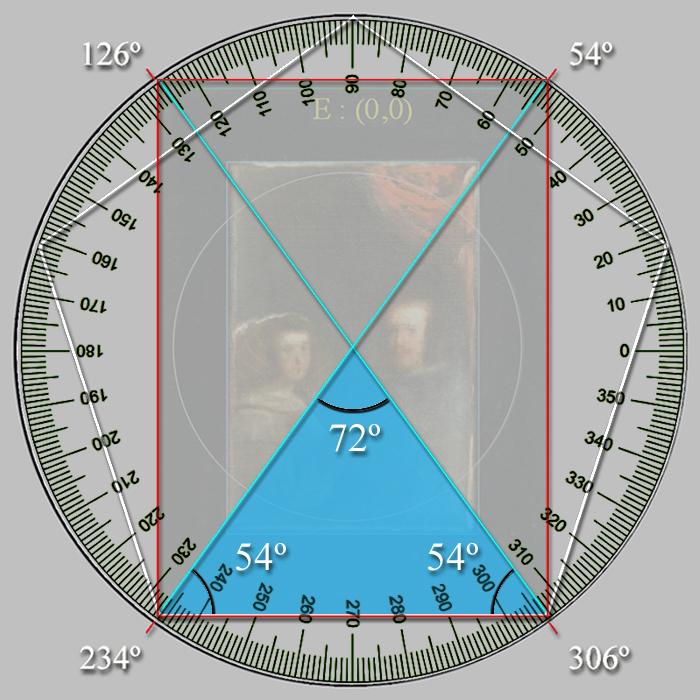 |
|
|
Estos resultados reflejan una exactitud extrema propia de la ingeniería o la óptica, que en la práctica de la pintura no se requiere, ya que hablamos de una pintura al óleo elaborada con un pincel.
Y aunque esta precisión tiene el propósito lógico de asegurar el dibujo, sin embargo, también funciona como sustento invisible de la perfecta matemática en esta obra de Velázquez, revelando, pues, una intencionalidad indetectable a un nivel de medición convencional, como es el ejemplo del Espejo de Las Meninas, que se convierte en un portal de distintos códigos que unifica la geometría sagrada, la proporción áurea y a la Kabala con la monarquía, otorgando legitimidad y poder divino a la corona española.
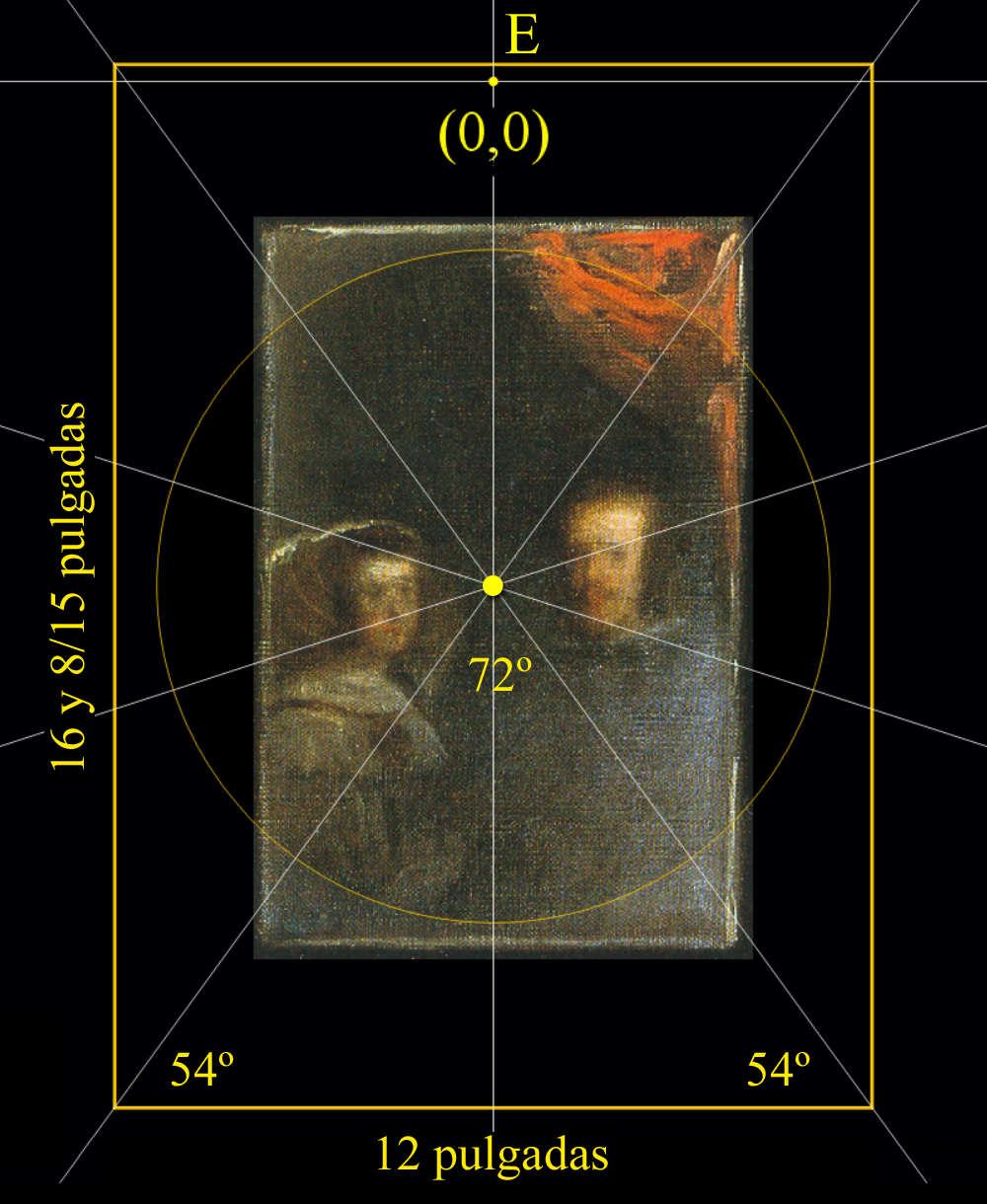 |
|
|
El Centro físico
Estudiaremos esta obra artística teniendo
en cuenta dos ideas necesarias;
La Geometría de esta composición como un espacio cuadrado,
y el aspecto final de Las Meninas después del estrechamiento o corte por su lateral izquierdo.
Las medidas vigentes del lienzo de Las Meninas no son las medidas exactas que utilizó el maestro Velázquez, por lo que utilizaremos un cuadrado de ayuda, cuyo centro se sitúa en la parte superior del marco del espejo, para analizar el formato original de este lienzo.
Este gran cuadrado de ayuda mide 155,25 unidades de lado, que equivalen en el sistema métrico a 3,2085 metros, mientras que en el castellano corresponden a 11 pies y medio, o sea 138 pulgadas, y se extiende hasta lo que hemos dado en llamar:
Borde del orillo del lino original.
Este nuevo planteamiento se basa en la disponibilidad de dividir entre dos
138 pulgadas, que es igual a 69 pulgadas, y, de este modo, deducir el punto medio de la pared del fondo de Las Meninas.
Recordaríamos que la anchura del lienzo de Las Meninas era de 120 pulgadas, pero que en la actualidad es de 118 pulgadas y 7/9, que equivalen a 133,625 unidades, y que corresponden a 2,761583... metros.
Hablamos, pues, de un gran cuadrado superpuesto al lienzo que ha confirmado la posición exacta del verdadero borde del perímetro del lienzo original sobre el orillo en el lateral derecho de Las Meninas.
 |
|
DESGLOSE DE LA ANCHURA DE LAS MENINAS
|
69 pulgadas + 49 pulgadas y 7/9 = 118 pulgadas y 7/9 = 2,761583... metros.
Y concebida la anchura de esta pintura a partir de un perfecto cuadrado, se deduce que la altura del lienzo original de Las Meninas medía el doble del ancho de la distancia entre el centro del espejo y el borde del orillo del lino original en el canto derecho del moderno bastidor.
69 pulgadas × 2 =
138 pulgadas.
El punto E trata del centro de coordenadas, [0, 0], situado en la parte superior de la moldura del Espejo, mientras que el punto F es el Centro físico, y es, por tanto, el centro de Las Meninas tal cual las contemplamos en el Museo del Prado.
Aunque el punto
F es el Centro físico del lienzo de Las Meninas se le adivina en dos posiciones diferentes;una en base a la anchura actual de esta pintura,
y la otra es a causa de un fragmento desestimado en el lado izquierdo de la anchura original de 120 pulgadas, lo cual provoca un leve cambio de posición del Centro físico de la creación velazqueña.
Nos hallamos, pues, ante una anomalía que depende de la distancia entre la nariz de la Infanta Margarita, punto medio y eje de toda la superficie de Las Meninas, y su ojo izquierdo.
 |
|
|
El punto F del 1º Caso es el centro inicial del lienzo de Las Meninas.
Es decir:
Horizontal : 10,125 unidades
Vertical : 0,375 unidades
Las Meninas
se compone de la unión de tres franjas de
lienzo cosidas; dos de ellas tienen el ancho de fabricación, y una tercera, más
estrecha, completa la anchura total de la tela, si bien, habría que detallar oportunamente las
características de este
lienzo:
|
Esta obra está forrada con el sistema tradicional de la gacha. El soporte original está formado por la unión de tres bandas de lienzo de lino, colocadas verticalmente, es decir, en el sentido de su fabricación; la central y la lateral derecha presentan todo el ancho de la tela, ya que se puede observar el orillo en el borde derecho que dobla sobre el bastidor.
La banda lateral izquierda es de menor tamaño y no se observa el orillo; tal vez fue cortada por Velázquez, para conseguir unas determinadas dimensiones en la composición... [18]. |
Las anchura de las dos bandas de tela de la derecha de este lienzo son del mismo tamaño.
Caso Cuarto
La investigadora Carmen Garrido Pérez propone en su libro: VELÁZQUEZ, TÉCNICA Y EVOLUCIÓN - MUSEO DEL PRADO, 1992, un ancho de lienzo para la realización de Las Meninas de aproximadamente 105 centímetros.
Esto viene a ser 45 pulgadas × 0,02325 metros la pulgada = 1,04625 metros.
 |
|
|
|
banda del lienzo izquierda |
banda del lienzo central |
banda del lienzo derecha |
Total de la Anchura del lienzo actual |
|
31 pulgadas y 4/9 |
43 pulgadas y 2/3 |
43 pulgadas y 2/3 |
118 pulgadas y 7/9 |
|
0,731083333 metros |
1,01525 metros |
1,01525 metros |
2,761583333 metros |
|
|
|
banda del lienzo izquierda |
banda del lienzo central |
banda del lienzo derecha |
Total de la Anchura del lienzo original |
|
32 pulgadas y 2/3 |
43 pulgadas y 2/3 |
43 pulgadas y 2/3 |
120 pulgadas |
|
0,7595 metros |
1,01525 metros |
1,01525 metros |
2,79 metros |
|
|
Aunque es más probable que la anchura de estas tres piezas de lino en el telar midiesen respectivamente:
32 + 44 + 44 = 120 pulgadas.
Ante estas conclusiones podemos ya hablar de la cantidad exacta de lienzo que Velázquez dispuso para
su labor, y asegurar, por tanto, el análisis físico de esta pintura.
|
|
unidades |
pulgadas |
metros |
medidas castellanas |
|
Anchura |
135 |
120 |
2,79 |
120 pulgadas / 12 = 10 pies |
|
Altura |
155,25 |
138 |
3,2085 |
138 pulgadas / 12 = 11 pies y medio |
|
|
Sin duda, 3,2085 metros era el tamaño de
la altura del lienzo de Las Meninas antes de ser montado en su bastidor original.
La altura
pictórica de 3,2085 metros la hemos considerado teniendo en cuenta dos factores:Que la acotación del borde del larguero superior estuviera promediado con el inferior.
Y que su lateral derecho solapase exactamente sobre el
El tamaño del lienzo de Las Meninas, o
cualquier retrato u objeto pintado en esta bella pintura, depende íntegramente de las
proporciones regulares.
Caso Quinto
Partimos de las medidas del lienzo que ya han sido consideradas en el apartado anterior.
Los tamaños de la anchura y altura del lienzo original de Las Meninas miden;
120 pulgadas para la anchura,
y 138 pulgadas para la altura.
|
|
unidades |
proporción |
pulgadas |
metros |
medidas castellanas |
|
Anchura |
135 |
20 |
120 |
2,79 |
120 pulgadas / 12 = 10 pies |
|
Altura |
155,25 |
23 |
138 |
3,2085 |
138 pulgadas / 12 = 11 pies y medio |
|
|
La anchura de Las Meninas mide 120 pulgadas
Factorización de 2 × 2 × 2 × 3 × 5 = 120.
Los divisores del número 120 son 16:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120.
La altura de Las Meninas mide 138 pulgadas
Factorización de 2 × 3 × 23 = 138.
Los divisores del número 138 son 8:
1, 2, 3, 6, 23, 46, 69, 138.
| LA ALTURA | LA ANCHURA | |||||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||||
| 3,2085 | 138 | 155,25 | = | 155,25 × 1 | 135 × 1 | = | 135 | 120 | 2,79 | |||
| 67,5 × 2 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 77,625 × 2 | 45 × 3 | = | 135 | 120 | 2,79 | |||
| 33,75 × 4 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 51,75 × 3 | 27 × 5 | = | 135 | 120 | 2,79 | |||
| 22,5 × 6 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 25,875 × 6 | 16,875 × 8 | = | 135 | 120 | 2,79 | |||
| 13,5 × 10 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 6,75 × 23 | 11,25 × 12 | = | 135 | 120 | 2,79 | |||
| 9 × 15 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 3,375 × 46 | 6,75 × 20 | = | 135 | 120 | 2,79 | |||
| 5,625 × 24 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 2,25 × 69 | 4,5 × 30 | = | 135 | 120 | 2,79 | |||
| 3,375 × 40 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 1,125 × 138 | 2,25 × 60 | = | 135 | 120 | 2,79 | |||
| 1,125 × 120 | = | 135 | 120 | 2,79 | ||||||||
|
|
Al mismo tiempo, siendo el año 1656
cuando fueron pintadas Las Meninas por Diego Velázquez en Madrid,
eventualmente, la cifra de este año está equiparada, de manera manifiesta, con la
misma cantidad de líneas castellanas que hemos asignado a la altura de esta pintura.
Caso Sexto
Primero observemos los 24 divisores del número 1656:
1, 2, 3, 4, 6, 8, 9, 12, 18, 23, 24, 36, 46, 69, 72, 92, 138, 184, 207, 276, 414, 552, 828, 1656.
Y ahora establezcamos y demos nombre a su valor cuantitativo:
| Sistema castellano | varas | pies | palmos | pulgadas | líneas | puntos | metros | unidades |
| 3 y 10/12 | 11 y 6/12 | 15 y 4/12 | 138 | 1656 | 19872 | 3,2085 | 155,25 |
|
|
Por consiguiente, obtendríamos 138 pulgadas dividiendo 1656 líneas castellanas entre 12, resultado que se haya relacionado, a medida del deseo, con la misma cantidad de pulgadas que las del verdadero tamaño de la altura inicial del lienzo que analizamos.
1656 ÷ 12 = 138.
Y de igual manera la anchura funciona con los mismos guarismos:
1656 ÷ 13,8 = 120.
El arquitecto Ramiro Moya en su análisis: El trazado regulador y la perspectiva en Las Meninas, obtuvo las siguientes medidas para este lienzo de Diego Velázquez [19]:
23K para la altura y 20K para la anchura, valiendo K ≈ 1/2 pie = 0,139 metros.
|
LA ALTURA - 11 pies y medio |
LA ANCHURA - 10 pies |
|||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 3,2085 | 138 | 155,25 | = | 6,75 × 23 | 6,75 × 20 | = | 135 | 120 | 2,79 | |
|
|
Aunque el valor de K en nuestras operaciones matemáticas valga 0,1395 metros, que equivale a 6 pulgadas, estamos hablando de la mismas proporciones del lienzo de Las Meninas.
Y cierto es que el Pie Real mide 0,279 metros, y que la anchura de Las Meninas medía 2,79 metros, es decir, diez veces más; por fortuna una relación proporcional.
En definitiva, hemos establecido el punto de encuentro entre las distintas equivalencias geométricas, matemáticas y de aritmética castellana del tamaño de Las Meninas.
Paradigma liberal
La
publicación en 1925 del inventario de la
librería de Velázquez
por Sánchez
Cantón abrió la posibilidad de conocer los intereses literarios y científicos
del pintor [20].
Las materias del quadrivium, o cuadrivio, representan al conjunto de las cuatro artes liberales de la antigua Grecia y del mundo medieval. Ciencias de un mismo patrón teórico que han permanecido lejos de su aplicación, y posterior desarrollo, en la metódica investigación de la obra de Velázquez [21].
En la Chronographia de Francisco Vicente de Tornamira, Pamplona, 1585, libro que se hallaba en la biblioteca de Velázquez, se describe a las siete artes liberales con todo lujo de detalles:
|
De los antiguos Philoſophos dependieron las siete Artes que llamaron liberales, dignas de ſer deprendidas de la gente libre y noble; las quales ſon Grammatica, Logica, Rethorica, Muſica, Arithmetica, Geometria, y Aſtrologia. Las tres primeras van por tres diuerſos caminos a un meſmo fin, que es el conoſcimiento del razonar; porque la Grammatica ha coſideracion al bien o mal hablar. La Logica al verdadero o faſso. La Rhetorica, al polido o no polido; de manera que todas tres tratan del razonar. Las quatro poſtreras van tambien por quatro vias a un meſmo fin, que es el conoſcimiento de la cantidad. Porque la Arithmetica trata de la cantidad diſcreta, no contrayda de los numeros. La Muſica, de la cantidad diſscreta, contrayda aſon. La Geometria, de la cantidad continua, no contrayda a linea. La Aſtrologia, de la cantidad continua, contrayda a mouimiento; de ſuerte que todas quatro tratan de la cantidad. |
El quadrivium comprendía: Aritmética, Geometría, Astronomía, o Astrología, y Música.
Y con la finalidad de explicar la compleja estructura áurea de Las Meninas indagaremos, pues, en el primer tratado en castellano de Fortificación, dedicado al rey Felipe III, escrito por el capitán e ingeniero Chriſtoual de Rojas, y publicado en Madrid en 1598:
Teorica y Practica de fortificacion.
|
AL PRINCIPE
nueſtro ſeñor don Felipe.
SEÑOR.
Aviendo dado Dios à V. Alteza el mayor imperio del mundo, y todas las partes que ſon meneſter para merecerle, eſcuſado ſera tratar de lo que en la milicia (vna de las colunas en que ſe ſuſtentan las Monarchias) importa la fortificación: y tambien lo fuera tomar à mi cargo el eſcriuir eſta materia, ſi algun Eſpañol lo huuiera hecho; pero viendo que eſta nacion tiene mas cuydado de derribar las fuerças, y muros de los enemigos, que de enſeñar à fabricarlos (aunque no es lo vno contrario a lo otro) determinè abrirle camino, y poner en manos de V.A. eſte libro, para que viendole tan fauorecido, otros ingenios mas leuantados den perfecion à mi intento, ſacando à luz ſus talentos eſcondidos: en lo qual pienſo hazer à V.A. un gran ſeruicio: como quien deſcubre minas riquiſſimas, que aunque no puſo el deſcubridor el oro que dellas ſe ſaca, merece premio por auerle deſcubierto. Aſsi yo le eſpero por eſte libro, como inſtrumento que mouera los que le ſeguiran luego, de tan grandes ingenios, como V.A. tiene en ſu ſeruicio. Eſto es lo que ofrezco à V.A. con la humildad que ſe deue à ſu grandeza, y con la fidelidad y deſſeo, que en ocaſiones he derramado mi ſangre, y auenturado la vida por ſu Corona: en la qual, deſpues de los largos, y felizes dias del Rey nueſtro ſeñor, conſerue Dios a V.A. con aumento de Reynos, como la Chriſtiandad ha meneſter.
En Toledo à 8. de Iulio de 1596.
Chriſtoual de Rojas. |
|
Digo que ſe corte de tal manera la linea A.D. que el rectangulo de toda ella, y vna de ſus partes, ſea igual al quadrado, que ſe hiziere de la parte que reſta, que ſe hara por la 11. propoſicion del lib. 2. de Euclides, y como aqui parece en eſta figura, en que mueſtra que la linea A.D. ſe haga della vn quadrado, y luego el lado D.C. deſte quadrado ſe diuida en dos partes iguales en el punto E. y deſde alli ſe tirarà la linea E.A. y à la meſma diſtancia ſe dara la linea E.T. y de la frente de la T.D. ſe hara vn quadrado D.T.L.N. que es igual al rectangulo ſeñalado con la R. y todo el rectangulo mayor L.C. es igual al quadrado de A.D. hoc eſt D.G. de donde ſe ſigue, que la linea A.D: eſta cortada con eſtrema, y media razon, en el punto N. como ſe prueua por la proporcion 30. del lib. 6. de Euclides. |
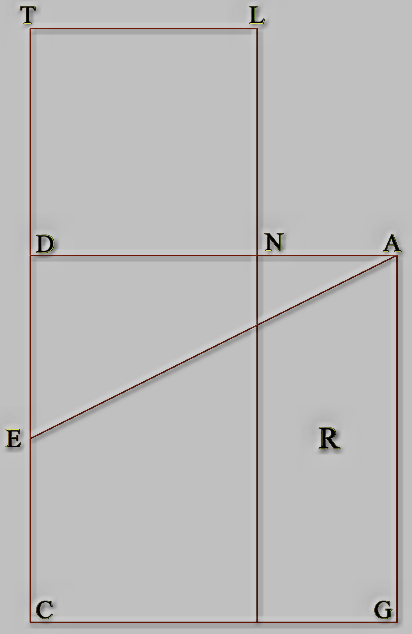 |
|
|
El punto de fuga áureo de Las Meninas
Para comprobar la presencia del número áureo en Las Meninas
deben trazarse los vectores a partir de puntos significativos;
por lo que a continuación analizaremos la
posición exacta del punto de fuga
áureo de este óleo de acuerdo con la Geometría de Los Elementos de Euclides:
Libro II - Problema 1 - Proposición 11
Dividir una recta AB en dos partes de modo que el rectángulo comprendido por la recta entera y por una de sus partes, ZCKI, sea equivalente al cuadrado de la otra parte, AB2.
|
|
|
Los Elementos de Euclides y Las Meninas
Libro II - Problema 1 - Proposición 11 |
Análisis
Euclides construye esta Proposición 11 a partir del cuadrado ABCD;
primero divide el lado AC en dos partes iguales mediante el punto O,
luego traza el segmento OB,
y extiende el lado COA hasta Z,
de manera que OB = OZ.
De esta forma se obtiene el punto T, y así se completa el cuadrado TIZA.
|
|
El punto T divide el segmento AB en media y extrema razón, de lo que se deduce que AB / AT = AT / TB.
El primero en hacer un estudio formal sobre el número áureo fue Euclides, que lo definió en su libro de Los Elementos del siguiente modo [22]:
Libro VI - Definición 3
Se dice que un segmento está dividido en media y extrema razón cuando el segmento total, AB, es a la parte mayor, AT, como la parte mayor, AT, es a la menor TB.
|
|
Los Elementos de Euclides y Las Meninas.
Análisis de acuerdo al tamaño del Límite de la rejilla de 152 unidades
Libro VI - Definición 3
Aquí se deduce que siendo AB = 152 unidades y AT = 94 unidades; luego el valor de TB sería de 58 unidades.
Es decir, la relación entre; AT = 94 unidades y TB = 58 unidades, se aproxima al valor del número de oro:
94/58 = 1,620689655... ≈ Φ

Matemáticamente: TB = AT2 / AB = 942 / 152 = 8836 / 152 = 58,13157895 unidades.
La diferencia es de 58,13157895 - 58 = 0,13157895 unidades, aproximadamente 2/15 de pulgada.
Si 1,125 unidades equivalen a 23,25 mm. [23].
0,13157895 unidades equivaldrán a 2,7192983 mm.
Esto significa que la perpendicular que nace en el punto I, y que pasa por el punto T, y cruzando el punto de fuga X finaliza su recorrido en el punto K, está desplazada hacia la derecha, según estos cálculos matemáticos, 2,7192983 mm. [24].
El punto de fuga de Las Meninas se ubica en la coordenada del punto X: [18, -12].
Esta división perfecta, que los antiguos llamaron áurea, prueba, pues, la posición exacta de la abscisa del punto de fuga X en relación con la figura de un cuadrado que mide 152 unidades de lado.
El Triángulo de Kepler
El Libro II - Problema 1 -
Proposición 11, de los Elementos de Euclides analizado en el apartado
anterior, es el antecedente necesario del propósito de Velázquez; aunque es
perentorio subrayar, que debido al interés del pintor español por este
tipo de Geometría, y, ante el vigor científico de esta época, el punto de
fuga áureo de Las Meninas quedó establecido en la
perpendicular de la altura del Triángulo de Kepler.
Cálculo de los dos ángulos agudos del Triángulo de Kepler:
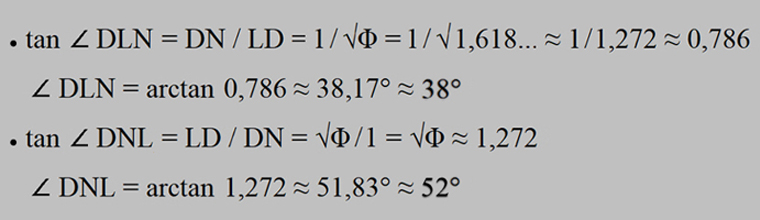 |
|||
|
ÁNGULO AGUDOS |
TOLERANCIA |
||
|
Cateto mayor |
DL | 38,17º ≈ 38º |
0,44... % |
|
Cateto menor |
DN | 51,83º ≈ 52º |
0,32... % |
|
|
|
|
|
LADOS |
MEDIDA ARITMÉTICA |
MEDIDA GEOMÉTRICA |
TOLERANCIA | |
|
Hipotenusa |
AE |
152 |
152 |
0 % |
|
Cateto mayor |
DA |
119,472... |
119,5 |
0,023... % |
|
Cateto menor |
DE |
93,936... |
94 |
0,068... % |
Matemáticamente se demuestra, pues, la relación entre dos segmentos que componen una misma línea, donde la longitud total del segmento, LN, dividida por su parte mayor, LM, es igual a la longitud del segmento de su parte mayor, LM, dividida por el segmento menor, MN.
| LN / LM = LM / MN ≈ 1,618033988... = Φ |
|
|
|
|
Estos datos permiten, pues, demostrar, que, aunque el dibujo sea en realidad ligeramente impreciso para llevarlo a la práctica, sin embargo, el razonamiento es correcto.
De manera, que el maestro español propuso la visualización del lienzo de Las Meninas a través de la progresión áurea de los tres lados del Triángulo de Kepler, y, consecuentemente, de las tres áreas cuadradas adyacentes del perímetro de este triángulo rectángulo áureo.
|
|
|
|
Nicolás Copérnico [25], para su satisfacción, tenía razón ante un Tolomeo aún vigente entre los distinguidos profesores del siglo XVI, y, sumándose a estas nuevas teorías planetarias, Johannes Kepler, matemático y astrónomo, publicaba en el año 1596 el MYSTERII COSMOGRAPHICI donde expresaba, en estos términos, su admiración por la proporción áurea:
|
Dos grandes tesoros tiene la Geometría; uno es el Teorema de Pitágoras, y, el otro, la división de un segmento en media y extrema razón:
Al primero lo podemos comparar a un montón de oro, y al segundo lo podemos llamar una piedra preciosa. |
 |
|
 |
|
 |
| Fuego | Tierra | Universo | Aire | Agua |
| tetraedro | hexaedro | dodecaedro | octaedro | icosaedro |
|
De Divina Proporción de Luca Pacioli |
|
Quo accedit & illud, atque hercle indicem digitum ad cauſam harum rerum occultiſisimam intendit, quod proximo capite habebimus: (17) duos nempe eſſe Geometriæ theſauros, vnum, ſubtenſæ in rectangulo rationem ad latera; alterum, lineam extrema & media ratione ſectam, quorum ex illo Cubi, Pyramidis & Octaedri conſtructio fluir, ex hoc verò conſtructio Dodecaedri & Icoſaedri.
Página - 41. CAPUT XII. Diuiſio Zodiaci, & aſpectus. MYSTERII COSMOGRAPHICI. M. Ioanne Keplero. TVBINGÆ. ANNO M. D. XCVI.
(17) Duos nempe esse Geometriae thesauros.
Duo Theoremata infinitae vtilitatis, eoque pretiosissima, sed magnum discrimen tamen est inter vtrumque. Nam prius, quod latera rectanguli possint tantum, quantum subtensa recto, hoc inquam recte comparaueris massae auri: alterum, de sectione proportionali, Gemmam dixeris. Ipsum enim per se quidem pulchrum est, at sine priori valet nihil: ipsum tamen promouet scientiam tunc vlterius, cum prius illud nos aliquatenus prouectos, iam destituit, scilicet ad demonstrationem et inuentionem lateris Decangularis, et cognatarum quantitatum.
IN CAPVT DVODECIMVM NOTAE AVCTORIS. Bearbeitet von Frankz Hammer. München. MCMLXIII. |
|
A esto se añade esto, y en efecto, señala con su dedo la causa más oculta de estas cosas, que discutiremos en el próximo capítulo: (17) que de hecho hay dos tesoros de la Geometría, uno, la relación de la hipotenusa en un triángulo rectángulo con los catetos; la otra, la recta dividida en extrema y media razón, que de la primera deriva la construcción del Cubo, la Pirámide y el Octaedro, y de la segunda en cambio la construcción del Dodecaedro y el Icosaedro.
Página - 41. CAPUT XII. Diuiſio Zodiaci, & aſpectus. MYSTERII COSMOGRAPHICI. M. Ioanne Keplero. TVBINGÆ. ANNO M. D. XCVI.
(17) Hay dos tesoros de la Geometría.
Dos teoremas de infinita utilidad, y por lo tanto de gran valor, pero con una gran diferencia entre ellos. En cuanto al primero, porque los lados de un rectángulo pueden ser tan largos como la longitud de una línea recta, digo que has comparado correctamente esto con una masa de oro; y al segundo, sobre la sección proporcional, lo has llamado una gema. Porque es ciertamente hermoso en sí mismo, pero sin el primero no vale nada: sin embargo, hará avanzar aún más la ciencia cuando ya nos ha fallado, habiéndose adelantado hasta cierto punto, es decir, hasta la demostración y descubrimiento del lado decagonal y cantidades relacionadas.
IN CAPVT DVODECIMVM NOTAE AVCTORIS. Bearbeitet von Frankz Hammer. München. MCMLXIII. |
|
|
|
1597 & 1543 |
Al año siguiente, 1597, Michæl Mästlin, uno de los primeros en aceptar y enseñar el heliocentrismo copernicano, envió en una carta a su exalumno Kepler el cálculo exacto del número de oro Phi [26].
|
Problema de triangulo rectangulo, cujus latera in continua proportione.
Fig. VIII. Tab. A. |
Tua propoſitio de triangulo rectangulo, cujus latera ſint in continua proportione, mihi vehementer placet, ejusque demonſtratio bona eſt. Numeros addo. Si ad E trianguli rectanguli ea ſit ſtructura, ut DF perpendicularis hypothenuſam AE in F ſecundum extreman & mediam rationem fecet, AE autem ſit decem partium erit AF, eique æqualis ED, √125 - 5 & EF 15 - √125. quadratum vero ED2, quod eſt 150 - √12500. ablatum ex quadrato AE2 100, relinquit quadratum AD2 √12500 - 50. cujus latus eſt AD. Igitur proportionalia ſunt:
Et hæc eſt vera proportio quæſita, quæ ſimili modo initium, ſicut hic à latere AE, ita etiam à latere AD vel ED habere poſſet. De hac cum Domino D. Magaro hactenus propter creba impedimenta conferre non potui, fiet tamen id prima quaque occaſione. |
El Triángulo de Kepler combina cuatro conceptos claves de Geometría y Matemática;
el Teorema de Pitágoras,
el número áureo,
la proposición 47 de los Elementos de Euclides [27]
y el Teorema de Tales de Mileto, que afirma que cualquier ángulo inscrito en un semicírculo es un ángulo recto.
|
|
|
|
| AE / AF = 152 / 94 = 1,617021276... ≈ Φ |
La vertical que pasa por el punto F, correspondiente a la medida 94 unidades, como hemos ya mostrado, también transita a través del punto de fuga X, y se halla ligeramente desplazada hacia la derecha, respecto al valor de Phi, 2,7192983 mm.
La cuadrícula Límite de la rejilla de 152 unidades sitúa a la Geometría áurea del lienzo de Las Meninas en su emplazamiento correcto.
| Cuadrículas | Valor - AE | Valor - FE | Valor - AF | AF / FE = Φ |
| Línea de acotación | 144 | 54 | 90 | 90/54 = 1,666666666 |
| Límite de la rejilla de 150 unidades | 150 | 57 | 93 | 93/57 = 1,631578947 |
| Límite de la rejilla de 152 unidades | 152 | 58 | 94 | 94/58 = 1,620689655 |
| Phi - Φ | 1,618033988... | |||
| 153 / 1,125 = 136 pulgadas | 153 | 58,5 | 94,5 | 94,5/58,5 = 1,615384615 |
| Borde del orillo del lino original | 155,25 | 59,625 | 95,625 | 95,625/59,625 = 1,603773585 |
|
|
Un Triángulo de Kepler es un triángulo rectángulo cuyos tres lados están formado, a su vez, por tres cuadrados cuyos lados y áreas se hallan en progresión geométrica de acuerdo con la proporción áurea.
Y puesta en práctica esta progresión geométrica en el Arte pictórico de Las Meninas tendríamos:
|
Progresión geométrica de Kepler
Y aplicando el Teorema de Pitágoras obtendríamos:
|
|
|
El Triángulo de Kepler y el lienzo de Las Meninas - [28] |
En definitiva, el Triángulo de Kepler es un triángulo rectángulo con lados y áreas en progresión geométrica.
Escribe Michæl Mästlin:
| Si ad E trianguli rectanguli ea ſit ſtructura, ut DF perpendicularis hypothenuſam AE in F ſecundum extreman & mediam rationem fecet (...) |
Michæl Mästlin se está refiriendo al Libro VI - Definición 3 de de los Elementos de Euclides:
|
Se dice que un segmento está dividido en media y extrema razón cuando el segmento total, AE, es a la parte mayor, AF, como la parte mayor, AF, es a la menor, FE. |
Y dando al lado AE el valor 1 conectaríamos la localización del punto de fuga áureo con el análisis del ancho del lienzo de Las Meninas.
|
|
|
|
|
AD = 1/√Φ = 0,786151377...
DE = 1/Φ = 0,618033988...
AE = 0,786151377... ^2 + 0,618033988... ^2 = 0,999999999... |
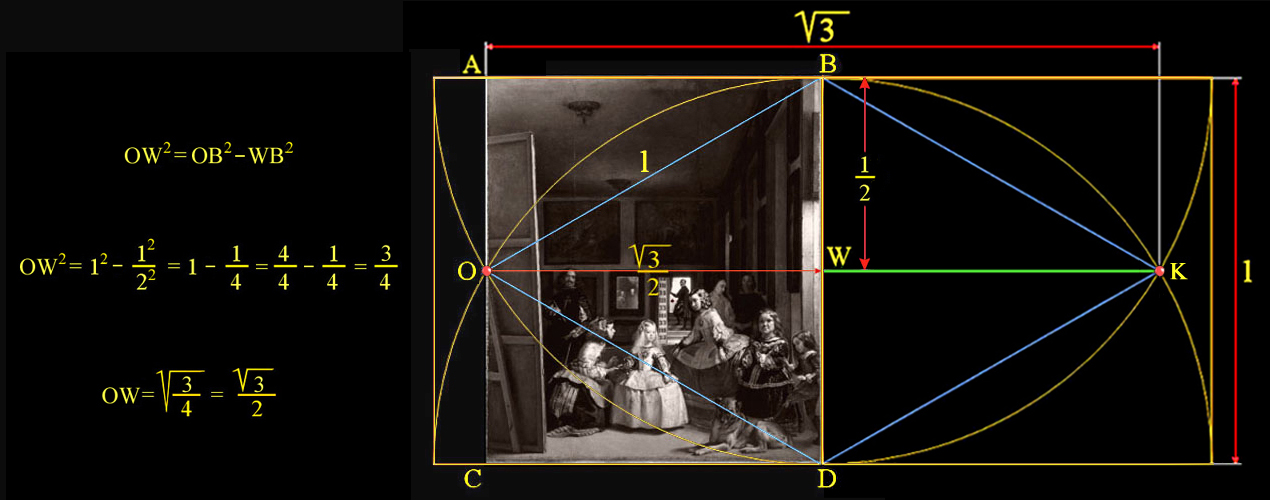 |
|
|
Hablamos, pues, de un tipo de lenguaje visual con el que se materializa el entendimiento con esta pintura, y de una Geometría exacta avalada por el número áureo, también llamado:
número de oro,
número de Dios,
razón extrema y media,
razón dorada,
media áurea,
proporción áurea
y divina proporción.
El número, como principio omnipresente en el Universo, ordena el arte de Las Meninas.
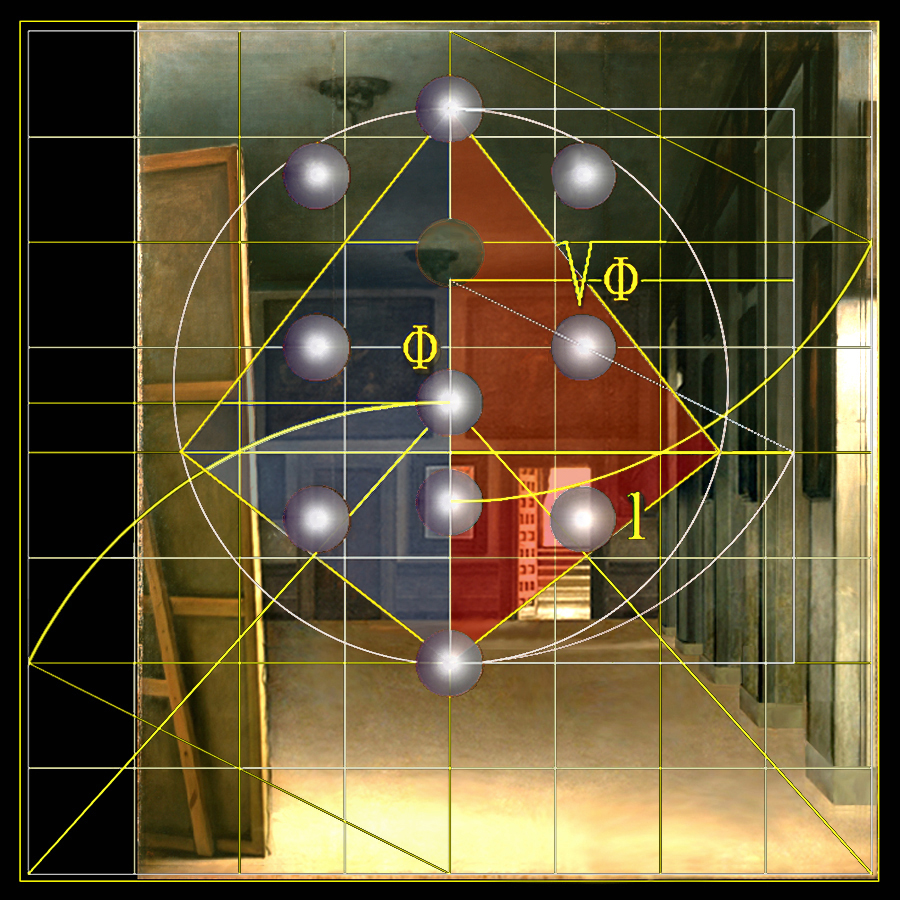 |
|
|
Velázquez en el proceso creativo de su lienzo plantea, pues, una doble Geometría áurea:
Una, como hemos ya analizado, condiciona el formato y la visualización del lienzo de Las Meninas,
y la otra se descubre en el tamaño de 100 unidades de la altura del eje central del Árbol de la Vida, ya que corresponde a la hipotenusa AE de la base del Triángulo Rectángulo Áureo de Kepler.
|
|
|
DOBLE ESTRUCTURA ÁUREA DE LAS MENINAS |
Y esta segunda propuesta áurea fue posible porque la distancia entre el centro de la Sefira nº 1, Kether, Corona: (0, 62) y el centro de la Sefira nº 10, Malkut, Reino: (0, -38), mide 100 umidades, es decir; un múltiplo de 10 de acorde al punto (3) Latus AE 10 = 10 del análisis del Problema del triángulo áureo del año 1597 planteado por Michæl Mästlin, el maestro de Kepler,
 |
|
|
Ahora se sabe que esta carta de 1597 no se la envía Mästlin a Kepler, sino Kepler a Mästlin, en donde Kepler describe la construcción de un triángulo rectángulo cuyos lados están en progresión geométrica, y que actualmente se denomina triángulo de Kepler, y, sin embargo, él atribuyó la autoría a Magirus:
 |
AE |
AD |
ED |
|
10 |
√61,803398... |
√125 - 5 |
|
|
10 |
7,861513... |
6,180339... |
|
|
MICHÆL MÄSTLIN |
|||
|
Φ |
√Φ |
1 |
|
|
1,618033... |
1,272019... |
1 |
|
|
100 |
78,615097... |
61,803398... |
|
|
VELÁZQUEZ |
|||
|
|
En conclusión, y recalcamos, Velázquez plantea, pues, una Geometría áurea en el trazado del Árbol de la Vida de Las Meninas, ya que la altura de su eje central corresponde a la misma hipotenusa AE de la base del Triángulo Rectángulo Áureo de Kepler.
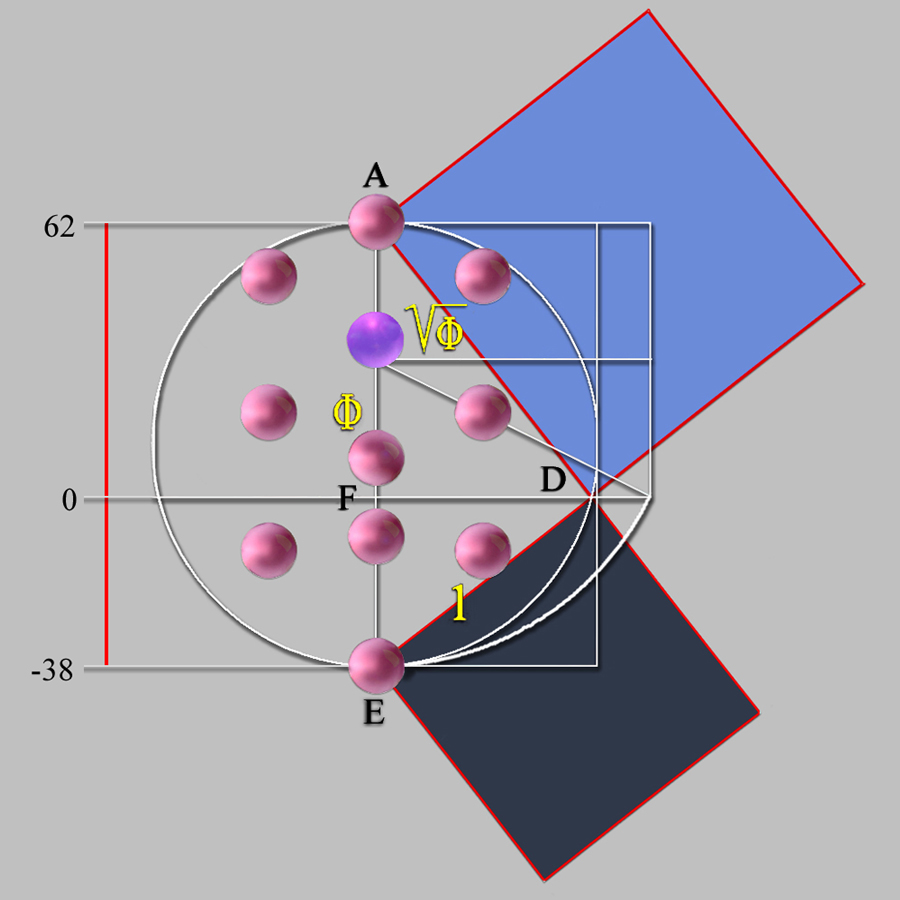 |
|
|
Si bien, en este renglón habría que subrayar, pues, que las medidas de los tres lados del triángulo áureo que descubrimos en el aire de Las Meninas no sólo tratan de cifras, sino cantidades en unidades que son equivalentes, por tanto, a las pulgadas castellanas.
|
AE |
AD |
ED |
|
Φ |
√Φ |
1 |
|
1,618033... |
1,272019... |
1 |
|
100 unidades |
78,615097... unidades |
61,803398... unidades |
| 88,888888... pulgadas | 69,880086... pulgadas | 54,936353... pulgadas |
 |
|
|
Y, como remate a estos argumentos de Geometría áurea, añadiremos, pues, el que plantea Michæle Stifelio en su libro Arithmetica Integra en 1544, que, como se puede comprobar, viene a ser la misma demostración que Johannes Kepler expuso 53 años después, no obstante, Kepler fue quien se llevó los laureles de este descubrimiento.
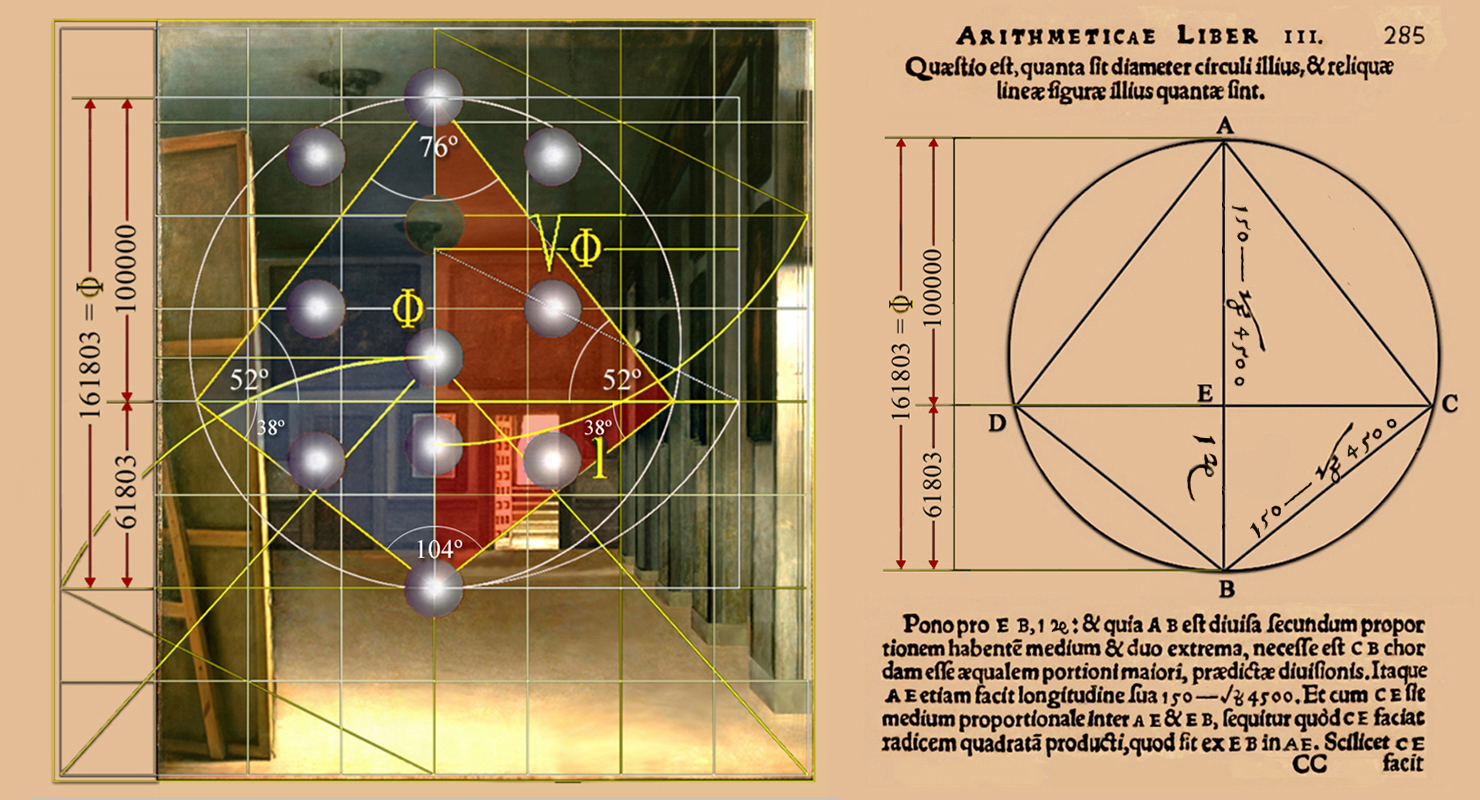 |
|
ARITHMETICAE LIBER III.
Quæſtio eſt, quanta ſit diameter circuli illius, & reliquæ lineæ figuræ illius quantæ ſint.
Pono pro E B, 1: & quia AB esſ diviſa ſecundum proportionem habentem medium & duo extrema, neceſſe eſt CB chordam eſſe æqualem portioni maiori, praedictae diuiſionis. Itaque AE etiam facit longitudine ſua 150/√4500. Et cum CE ſie medium proportionale inter AE & EB, ſequitur quod CE faciat radicem quadratam producti, quod ſit ex EB in AE. |
LIBRO III DE ARITMÉTICA.
La cuestión es, cuanto mide el diámetro de este círculo, y cuáles son las longitudes de las restantes líneas de esta figura.
Pongo para EB, 1, y puesto que AB está dividida según la proporción que tiene medio y dos extremos, es necesario que la cuerda CB sea igual a la porción mayor de la predicha división. Así pues, AE también mide en su longitud 150/√4500. Y puesto que CE es la media proporcional entre AE y EB, se sigue que CE resulta de la raíz cuadrada del producto que resulta de EB por AE.
|
|
Conclusión:
Siempre que DC valiera 2 se cumpliría esta igualad:
AB = (√5 + 1) = 2Φ = 3,236067...
Solución gráfica de DB:
|
El diámetro AB, del estudio geométrico de Michæle Stifelio de 1544, corresponde en el Árbol de la Vida de Las Meninas a la distancia AE entre el centro de la Sefira nº 1, Kether, La Corona: (0, 62) y el centro de la Sefira nº 10, Malkut, El Reino: (0, -38), distancia que mide, exactamente, 100 unidades.
Descubrir a Phi
Velázquez, en vez de menospreciar a la ciencia, se tomó el medio y
ventaja de expresar sus ideas más privadas en el arte de la pintura, y como
artista erudito tuvo que enfrentarse, al menos, a cuatro frentes distintos:
En el terreno religioso constituía un grave peligro cualquier tipo de información que pudiera relacionar a un individuo con el credo judío, aun cuando se hubiese convertido al catolicismo de buena fe.
Al científico, donde la Teología Católica se la consideraba como la ciencia más alta del conocimiento.
A la Astrología, que desde el 5 de enero de 1586 la bula papal promulgada por Sixto V, Cœli et terræ creator, condenaba con penas graves a los que la ejerciesen.
Y a la Kabala.
Es evidente que estos cuatro puntos son muy controvertidos, pero justifican la inquietud y singularidad de Diego Velázquez.
Sabemos, pues, que la palabra Jehovah, el nombre de Dios más importante en el judaísmo, está formada por las cuatro letras del Tetragrama YHVH, y que gracias a la Gematría se verifica la relación de estas cuatro letras hebreas con la proporción áurea.
|
|
TETRAGRAMA
Nombre de Jehovah y el valor Phi
Los números de la sucesión; 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144..., de Fibonacci.
|
|
La Espiral
de Fibonacci y el valor Phi
La proporción áurea de estos rectángulos viene determinada por el cociente entre las medidas de sus lados:
1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ...
|
Sucesión de Fibonacci |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
|
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
|
Aproximación a Phi |
1 |
2 |
1,5 |
1,6666 |
1,6 |
1,625 |
1,615 |
1,6190 |
1,6176 |
1,6181 |
1,6179 |
A medida que los rectángulos de la Sucesión de Fibonacci se van haciendo más grandes sus formas se van acercando al rectángulo áureo.
Esta sucesión de cocientes tiende a estabilizarse en un número próximo a 1,618.
Es decir; el valor del número áureo:
|
|
|
|
Se entiende, pues, que lo divino es sagrado, y lo sagrado divino, y que la superficie de Las Meninas está organizada a partir de una cuadrícula, en la que Velázquez, al igual que los grandes matemáticos de la época del barroco, introdujo su ideal geométrico de acuerdo a sus descubrimientos.
|
|
|
3º Caso
Localización del punto de fuga áureo |
Habría que resaltar, pues, que la Geometría áurea, que hemos investigado en el lienzo de Las Meninas, tiene la totalidad de sus puntos concebidos en un sólo plano con el objeto de identificar la posición de cada coordenada.
En el mismo siglo XVII, mientras que la Teología Católica condenaba en El Índice ideas científicas, Velázquez consolidaba en Las Meninas, adicionalmente, la relación entre La Geometría áurea y El Árbol de la Vida.
 |
|
|
En la marca del suelo 0 arranca las distintas alturas hasta la marca 1,1666, que corresponde, pues, a la altura del canto superior de Las Meninas, lo que completa la altura total de 140 pulgadas:
138 pulgadas corresponden al tamaño exacto de la altura de lienzo que Velázquez dispuso para su labor, y más dos pulgadas de separación entre la parte inferior del lienzo y el propio suelo de la Habitación del Príncipe.
|
Elemento |
Valor geométrico | unidades | pulgadas | metros |
| Borde del orillo superior del lienzo | 1,1666 | 157,5 | 140 | 3,255 |
| Altura del Bastidor | 1 | 135 | 120 | 2,79 |
| Arista del techo | 0,8666 | 108,5 | 104 | 2,418 |
| Centro Sefira nº 6 | 0,6555 | 88,5 | 78,6666 | 1,829 |
| Centro de coordenadas | 0,5888 | 79,5 | 70,6666 | 1,643 |
| Horizonte | 0,5 | 67,5 | 60 | 1,395 |
| Línea de tierra | 0,3666 | 49,5 | 44 | 1,023 |
| Borde del orillo inferior del lienzo | 0,0166 | 2,25 | 2 | 0,0465 |
| Suelo | 0 | 0 | 0 | 0 |
|
|
Y entendemos, pues, que sin ciertas consideraciones se derrocharía tiempo y talento adentrarse en la Habitación del Príncipe; y de ahí que hayamos abierto la mano, para que futuras incursiones en este óleo, en todos los casos, cuenten con un firme punto de apoyo.
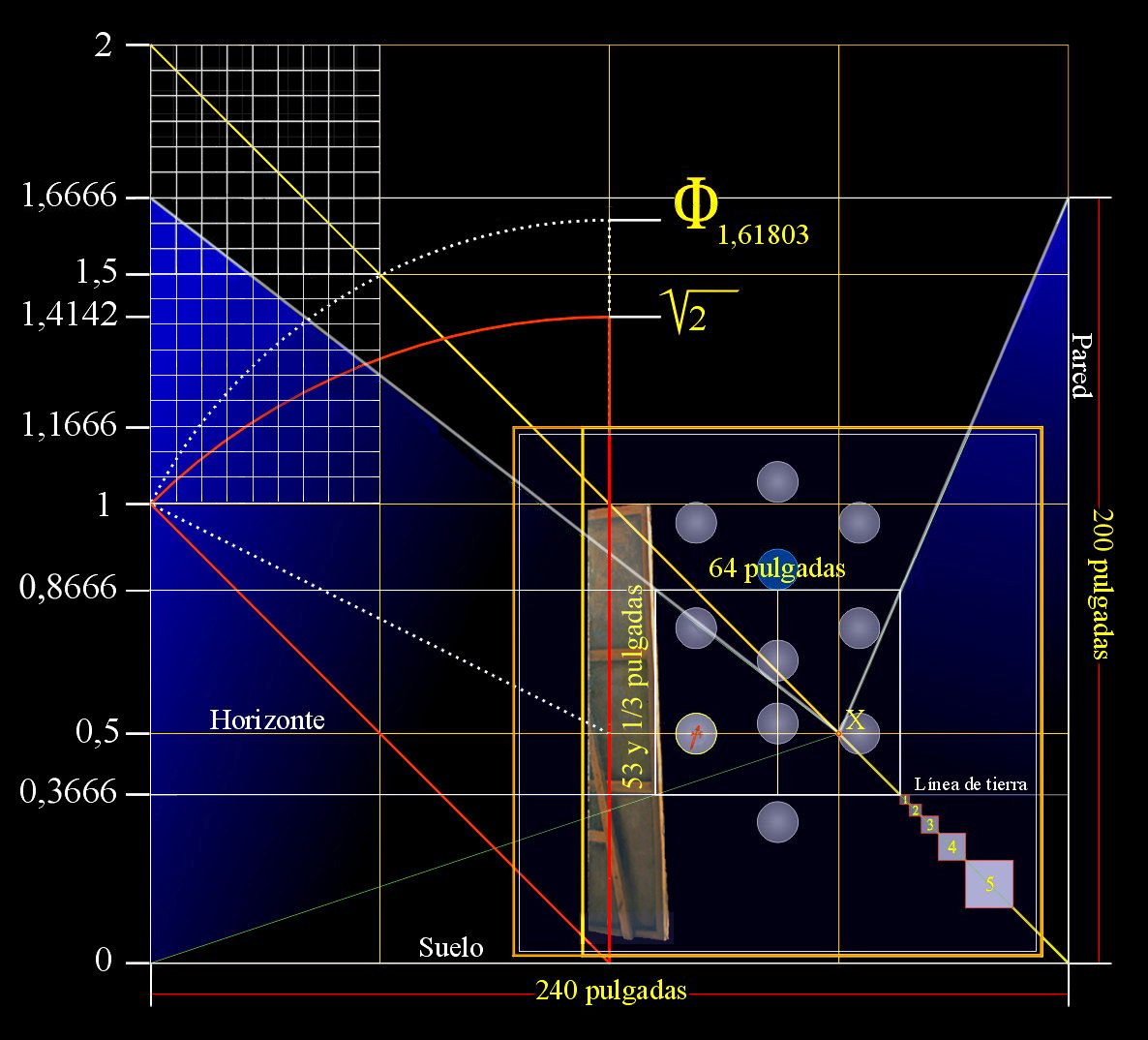 |
|
|
Las medidas del tamaño real de la Habitación del Príncipe tienen la siguiente relación:
|
Habitación del Príncipe |
Metros |
Pulgadas |
Unidades |
Valor geométrico |
Ratio |
|
Altura |
4,65 |
200 |
225 |
1,6666 |
0,8333 |
|
Anchura |
5,58 |
240 |
270 |
2 |
|
|
Representando el valor 2 la máxima altura geométrica de la Habitación del Príncipe, que equivale a 240 pulgadas, entonces el valor geométrico 1,6666 equivaldría a 200 pulgadas, cantidad que corresponde a la altura real de esta sala de Palacio.
Y añadiríamos; que para que la altura real de la Habitación del Príncipe perteneciera a la Sucesión de Fibonacci debería ajustarse a la altura geométrica de 1,625.
Es decir: 13/8 = 1,625.
|
Habitación del Príncipe |
Valor geométrico |
Pulgadas |
|
Valor de la Pulgada |
|
Metros |
Unidades |
|
Altura |
1,6666 |
200 |
× |
0,02325 metros |
= |
4,65 |
225 |
|
1,625 |
195 |
× |
= |
4,53375 |
219,375 |
Y llegado el caso, también podríamos considerar la construcción de un cuadrado a partir de un círculo donde se demuestra que el lado del cuadrado y el radio del círculo se encuentran en relación áurea.
Sea l + √5 el tamaño del lado del cuadrado ÁBDC´, y 2 el radio Oh del círculo, que divididos entre sí se deduce el valor de Phi.
1 + √5 ÷ 2 = Φ
Phi = 1,61803...
|
|
|
|
22 años antes de que se pintaran Las Meninas encontramos al final del Libro VI de Diofanto de Alejandría, de Les oeuvres mathematiques de Simon Stevin de Bruges editado en Leyden en 1634, un comentario acerca del valor del número Phi.
Póstumamente, pues, Albert Girard, 1599 - 1632, dejó constancia en el libro de Simon Stevin una manera ingeniosa de plantear la proporción áurea.
Comenta el matemático francés acerca de la línea dividida en media y extrema razón:
|
; & pour exemple ſoit propoſe d´explicquer par des rationaux la raiſon des ſegmens de la ligne coupeé en la moyenne & extreme raiſon, ſoit faicte une progreſſion: 0, 1, 1, 2, 3, 5, 8, 13, 21, &c. dont chaſque nombre ſoit egal aux deux precedens, alors deux nombres pris immediatement denotteront la meſme raiſon, come 5 á 8 ou 8 á 13 &c.& tant plus grands, tant plus pres, comme ces deux 59475986 & 96234155, tellement que 13, 13, 21 conſtituent aſſez preciſement un triangule Isoſceles ayant l´angle du pentagone; |
El valor de Phi según Albert Girard sería: 96234155 / 59475986 = 1,618033789... ≈ Φ.
Phi y la unidad
|
|
[1/Φ] ≈ 0,618033988... + [1/Φ2] ≈ 0,381966011... = 1.
4º Caso
Localización del punto de fuga áureo en la rejilla de 152 unidades de lado
|
|
En esta fórmula 1/Φ2 equivale a la distancia entre el punto de fuga y el lateral derecho de la rejilla de 152 unidades.
El rigor geométrico
La invención de la perspectiva
se remonta al año 1416, cuando Filippo Brunelleschi fijó
en el punto de fuga
la reducción
matemática absoluta de las tres
dimensiones del espacio
descriptivo en un soporte bidimensional [29].
Aunque habría que reseñar que la perspectiva de la pintura italiana, a diferencia del modelo flamenco basado en la observación directa de la realidad, se consolidó en la Geometría euclidiana.
5º Caso
Nacimiento geométrico del punto de fuga áureo
|
|
|
Elemento |
Valor geométrico |
pulgadas |
metros |
|
Altura total |
2 |
240 |
5,58 |
|
Altura real de la Habitación del Príncipe |
1,6666 |
200 |
4,65 |
|
Borde del orillo superior del lienzo |
1,1666 |
140 |
3,255 |
|
Altura del Bastidor |
1 |
120 |
2,79 |
|
Arista del techo |
0,8666 |
104 |
2,418 |
|
Horizonte |
0,5 |
60 |
1,395 |
|
Línea de tierra |
0,3666 |
44 |
1,023 |
|
Borde del orillo inferior del lienzo |
0,0166 |
2 |
0,0465 |
|
Suelo |
0 |
0 |
0 |
|
|
La perspectiva que utiliza Diego Velázquez interpreta la posición de cada detalle, tal y como se presentan ante la vista, siguiendo reglas geométricas consistentes.
De manera, que el espacio tridimensional de esta obra maestra depende del punto de fuga X en la coordenada: [18, -12], lo que viene a demostrar que, gracias al talante científico de Velázquez, todas las relaciones geométricas del lienzo de Las Meninas están trazadas en un único plano.
6º Caso
Localización de la altura del Horizonte de Las Meninas respecto al suelo de la Habitación del Príncipe
|
|
El Horizonte de la escena de Las Meninas, como causa de la realidad perfecta pitagórica, da acceso directo al reino de la verdad, e iguala su altura a la cuarta parte de la anchura total de la Habitación del Príncipe.
Al mismo tiempo, el ancho del lienzo de Las Meninas equivale a la mitad de la anchura de la Habitación del Príncipe, y la escala de la distante pared pintada corresponde a 1/3,75 de esta misma sala.

|
|
|
|
Zona izquierda 132 pulgadas |
Zona central 64 pulgadas |
Zona derecha 44 pulgadas |
||
|
44 |
44 |
44 |
64 |
44 |
|
Total - 240 pulgadas |
||||
|
|
Hemos recuperado, pues, el sistema de medidas castellano, lo que permite basarse en un modelo matemático exacto, que respalda la precisión del sistema de medición usado en todo momento de este análisis.
FORMATO 30
| Formato | Proporción | Pulgadas por unidad | La anchura | Tamaño en metros | ||||
| 30 | 30/9 | = | 3,333333 | × | 72 unidades | = | 240 pulgadas | 30 × 8 × 0,02325 = 5,58 metros |
|
|
| Formato | Proporción | Pulgadas por unidad | La altura | Tamaño en metros | ||||
| 30 | 30/9 | = | 3,333333 | × | 60 unidades | = | 200 pulgadas | 30 × 6,666 × 0,02325 = 4,65 metros |
|
|
 |
La anchura
Tamaño en unidades: 1,125 unidades por pulgada × 64 pulgadas = 72 unidades.
La altura
Tamaño en unidades: 1,125 unidades por pulgada × 53 pulgadas y 1/3 = 60 unidades. |
|
|
Se entiende, pues, que la escala de representación de la pared del fondo de Las Meninas es de: 1/3,75 = 0,266666...
A los objetos cuyas medidas cumplen con la proporción áurea se les atribuye una belleza especial, como es el caso del óleo de Las Meninas, cuya trascendencia áurea y simbólica, como ha sido probado, va acompañada de un legado sacro de primera magnitud.
Hablamos, pues, de una Geometría invisible que hace que las esferas que ilustran el ambiente aéreo de Las Meninas, denominadas los diez Sefirot, estén asentadas en un espacio perfecto.
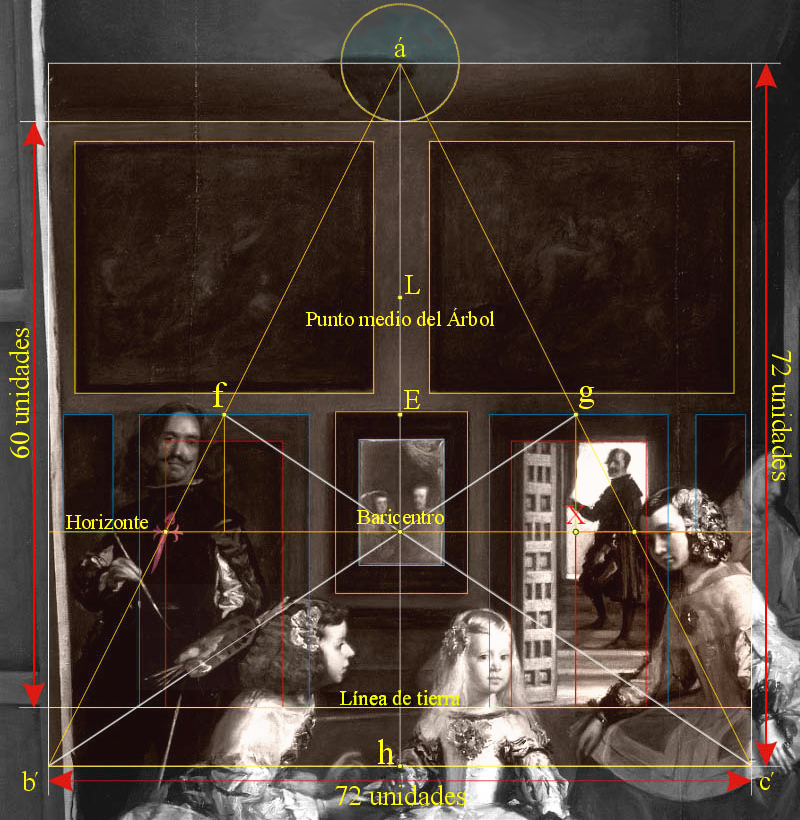 |
|
Intersección de las tres medianas del gran triángulo |
El descubrimiento de los números irracionales, y por tanto inconmensurables, por Hipaso de Metaponto causó una tremenda conmoción en la comunidad pitagórica, pues contradecía la máxima filosófica del gran matemático griego Pitágoras que llegó a basar toda su filosofía en la frase:
TODO ES NÚMERO
La leyenda afirma que Hipaso fue castigado a morir ahogado por introducir un elemento de desorden en un universo que los pitagóricos pretendían reducir a números naturales y proporciones.
El malogrado Hipaso de Metaponto descubrió que en la Geometría existen números que no pueden ser expresado como una fracción.
Posteriormente, Teodoro de Cirene, filósofo y matemático griego, probaría la irracionalidad de las raíces de los números enteros a base del método tradicional pitagórico.
La adecuación geométrica de Las Meninas, en la Habitación del Príncipe del antiguo Alcázar de Madrid, requirió del número irracional √3, que armoniza todas la medidas y coordenadas del plano inicial del lienzo [30]:
|
|
|
|
Hablamos, pues, de la representación ideal de la Habitación del Príncipe del Alcázar de Madrid.
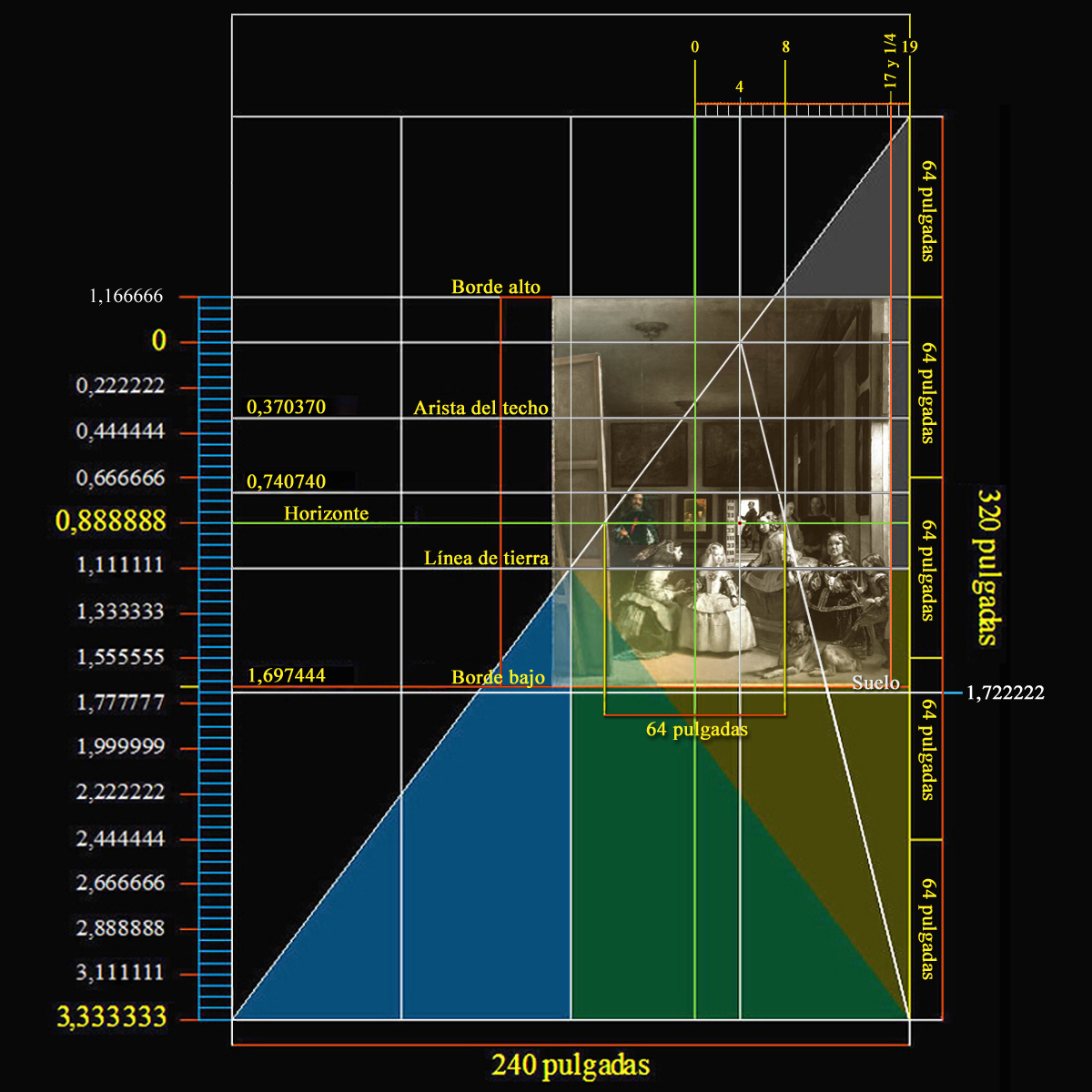 |
|
|
|
DEMOSTRACIÓN
Luego la escala de representación de la pared del fondo sería:
64 / 240 = 0,888888... / 3,333333... = 0,266666... = 1 / 3,75. |
Este plano mide físicamente 240 x 352 pulgadas, es decir; 5,58 x 8,184 metros.
| Lado del Triángulo | Cateto menor | Cateto mayor | Hipotenusa |
| Medidas en pulgadas | 80 × 3 = 240 | 80 × 4 = 320 | 80 × 5 = 400 |
| Divisiones | 60 × 4 partes | 64 × 5 partes | 100 × 4 partes |
|
|
El nombre de terna pitagórica deriva del teorema de Pitágoras, y consiste en una secuencia ordenada de tres números enteros positivos; a, b y c, que cumplen con el siguiente requisito:
a² + b² = c²
| Cateto menor a |
Cateto mayor b |
Hipotenusa c |
| 80 × 3 = 240 | 80 × 4 = 320 | 80 × 5 = 400 |
|
|
Este plano, basado en el Teorema de Pitágoras, prueba gráficamente la gestación del trabajo geométrico de Las Meninas, y permite reconstruir, con total exactitud, la localización de cada elemento necesario y principal de esta composición:
|
|
|
Localización del punto de fuga del lienzo de Las Meninas |
Este análisis confirma, pues, que la profundidad escalonada de los cinco planos laterales de la pared derecha de Las Meninas están convenientemente dispuestos de manera segura.
|
Intervalo |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
Unidades |
2,75 |
|
3,5 |
|
5 |
|
8 |
|
14 |
|
Pulgadas |
2 pulgadas y 4/9 |
|
3 pulgadas y 1/9 |
|
4 pulgadas y 4/9 |
|
7 pulgadas y 1/9 |
|
12 pulgadas y 4/9 |
|
Incremento |
|
+ 0,75 |
|
+ 1,5 |
|
+ 3 |
|
+ 6 |
|
|
Progresión |
|
0,75 × 20 |
|
0,75 × 21 |
|
0,75 × 22 |
|
0,75 × 23 |
|
|
|
|
|
|
Arranque de la perspectiva |
La condición simbólica
El método geométrico que mostramos no es
convencional, sino rigurosamente exacto, y prueba que la certera posición del punto de fuga áureo
X ha sido resuelta,
en cada Caso, con total grado de coherencia matemática; y, eso sí, hemos
definido, finalmente, la posición del pintor ante su lienzo.
Velázquez aseguró el tamaño de la anchura de la pared del fondo pintada en esta pintura en base al valor 0,02325 metros por pulgada, y utilizó el siguiente procedimiento para igualar la realidad con lo representado en Las Meninas:
FORMATO 8
| Formato | Proporción | Pulgadas por unidad | La anchura | Tamaño en metros | ||||
| 8 | 9/8 | = | 0,888888 | × | 72 unidades | = | 64 pulgadas | 8 × 8 × 0,02325 = 1,488 metros |
|
|
Unos números que se adaptan al cristalino del ojo en el acto espontáneo de mirar, y que, con vocación científica, coinciden con el tamaño del ángulo visual de Las Meninas.
|
|
|
|
Este infinito áureo converge con la Geometría Sagrada, que como lenguaje simbólico no se limita al simple uso de figuras y formas, sino que es una ciencia concebida para trascender ante el ojo del espectador.
Y al igual que el pensamiento pitagórico estaba supeditado a las matemáticas y la mística, esta pintura demuestra, de manera rotunda, el logro de una pintura perfecta gracias al buen manejo de la luz y la acertada ejecución de cada detalle.
| Proporción | Unidades | Pulgadas | Varas | Tamaño en metros |
| 7 cabezas y media | 20,25 | 20,25 / 1,125 = 18 | 36 / 2 = 18 = media vara | 18 × 0,02325 = 0,4185 |
|
|
| Tamaño en la distancia | Metros |
| 20,25 × 3,333333... = 67 pulgadas y 6/12 | 67,5 × 0,02325 = 1,569375 |
| 20,25 × 3,444444... = 69 pulgadas y 9/12 | 69,75 × 0,02325 = 1,6216875 |
| 20,25 × 3,555555... = 72 pulgadas | 72 × 0,02325 = 1,674 |
|
|
|
|
|
|
| Tamaño en la distancia | Metros |
| 26,25 × 3,333333... = 87 pulgadas y 6/12 | 87,5 × 0,02325 = 2,034375 |
| 26,25 × 3,444444... = 90 pulgadas y 5/12 | 90,416666... × 0,02325 = 2,1021875 |
| 26,25 × 3,555555... = 93 pulgadas y 4/12 | 93,333333... × 0,02325 = 2,17 |
|
|
Y aunque el uso de la Kabala podría ser considerado de alto riesgo, sin embargo, en el análisis que mostramos, ha sido la única ciencia auxiliar que ha confirmado el linaje de ciertas pinceladas de Las Meninas, lo cual da pie para pensar en la utilidad necesaria de esta nueva vía de investigación.
De lo que se deduce, por tanto, que los inconfesables menesteres del rey Felipe IV estaban en manos de su pintor Diego Velázquez.
En el tema de Las Meninas nos encontramos, fortuitamente, con Moisés camuflado en la textura del pelo de la menina Isabel de Velasco, que, como auspiciado profeta, se sitúa en el árbol Sagrado de la Vida en la Sefira nº 7 - Nectzah - La Victoria.
Descubramos, pues, este valioso detalle:
En un primer vistazo todo el mundo queda seducido por el bello aspecto venusiano que luce la menina Isabel de Velasco, pero, si se observa bien, su pelo negro se transforma en un encanecido personaje, que, retratado de perfil, mira hacia la luz principal procedente de la primera ventanas en dirección opuesta al semblante de la menina :
Una insospechada textura de alto brillo y gran contraste que desafía al tiempo.
|
|
El patriarca Moisés
Este nuevo personaje comparte con esta menina la posición de su oreja, tiene apariencia masculina, de tez morena y avanzada edad, poblada barba agrisada, de aspecto bíblico, mira hacia la luz que entra por la ventana de la derecha, tiene cara de suplicar y de estar en trance a la par, los toques de pintura blanca y oscura, además de ser texturados como pelos, son elementos caligráficos hebraicos. |
|
|
|
רֹאשׁוֹ, כֶּתֶם פָּז; קְוֻצּוֹתָיו, תַּלְתַּלִּים, שְׁחֹרוֹת, כָּעוֹרֵב׃
Su cabeza es un tesoro de oro fino, sus mechones le cuelgan, negros como el cuervo.
Cantar de los Cantares 5:11
La imagen del profeta Moisés conmueve profundamente en la primera toma de contacto, y nos hace exaltar con ganas al pintor español:
¡Gracias, Diego Velázquez!
|
|
|
|
Conocemos, a ciencia cierta, la identidad del personaje masculino consolidado en la cabeza de la menina que analizamos, porque, ya que los antiguos cabalistas asociaron los patriarcas bíblicos con las esferas del Árbol de la Vida según su naturaleza, Moisés, autor de la Torah y líder indiscutible de la Kabala, quedó representado al pie de la columna derecha.
IACOBI ZIEGLERI LANDAUI, en la página 524 de su libro Conceptionum in Genesim mundi, & Exodum, Commentarij impreso en Basileæ el año 1548, respalda esta aclaración sobre la séptima Sefira:
|
Ad ſeptimam referuntur, Adonai Sabaoth, crus, pes, columna dextera, rota magna, uiſio prophetiæ, Moyſes & cætera.
Al séptimo se refieren a; Adonai Sabaoth, la pierna, el pie, la columna derecha, la gran rueda, la visión de la profecía, Moisés y otros. |
Y, 105 años después, Athanasius Kircher, explica lo que se oculta tras la menina Isabel de Velasco, en la Sefira nº 7 Nectzah, en estos términos:
|
7 נצח Netſah Victoria, Æternitas |
Septimum veſtimentum Dei ſeu Sephirah dicitur נצח Netſah, id eſt, triumphus, victoria, ſeu æternitas, cui nomen יהוה צבאות Adonai Tſebaoth. Eius attributa ſunt, Crus, pes, columna dextera, rota magna, viſio Prophetæ. Canalis eſt, per quem Deus influit in Principatus, & per Intelligentiam Haniel in Cœlum Veneris. Plantarum cauſa & origo eſt. |
|
|
|
7 נצח Netzach Victoria, Eternidad |
La séptima vestidura de Dios es la Sefira denominada el Triunfo, Victoria o Eternidad, es decir; Netzach, cuyo nombre es יהוה צבאות, Adonai Tsebaoth. Sus atributos son: la pierna, el pie, la columna derecha, la gran rueda, la visión del Profeta. Netzach es el canal a través del cual Dios fluye hacia los Principados, y, a través de la Inteligencia de Haniel, hacia el Cielo de Venus. Es la causa y el origen de las plantas. |
|
CLASSIS IV. CABALA HEBRÆRVM - CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI. Tomus Secundus. GYMNASIVM. ROMÆ - Anno M DC LIII. |
La Sefira Nectzah representa la Victoria, la Eternidad, la visión de la profecía y al gobierno sobre las pasiones.
La Infanta Margarita y Phi
La
Geometría en la jornada de la reivindicación de la
heredera.
|
|
|
|
El Brazo florentino
A finales del siglo XV el
estudio de la proporción áurea fue de máximo interés, y no sólo la hallamos en
relación con la Matemática y obras de Arte, sino también con la concepción del cuerpo
humano, cuya altura media de tres Brazos constituye el fundamento del
Renacimiento italiano.
Retornemos a la antigua Mesopotamia, 4000 años antes de la era común, en donde se originaron distintos sistemas de medición basados en el tamaño del cuerpo humano, de cuyas proporciones surgió el patrón estándar de medidas antropométricas, y que, con cumplida mejora, se empleó en la ciudad de Florencia ligado al tiempo, ya que, como mostramos en la siguiente tabla, tomó de referencia en sus cálculos el desarrollo del ser humano.
| etapa | brazos | metros | meses | días | años |
| infancia | 1 | 0,5833.. |
6 |
180 |
1/2 |
| niñez | 2 | 1,1666... | 72 | 2160 | 6 |
| adolescencia | 3 | 1,75 |
216 |
6480 |
18 |
|
|
Analizaremos, pues, la unidad de medición denominada el Brazo florentino, cuyo tamaño estándar todavía se conserva en Florencia en un hueco de una fachada en Via de Cerchi donde antiguamente estaba depositado para la verificación de medidas lineales.
 |
|
|
58,333333... cm. / 20 soldi = 2,916666... cm., que es lo que mide 1 soldo.
Sí, hablamos del Brazo Florentino, el patrón de medidas que utilizó Leonardo da Vinci, que medía 58,333333... centímetros.
En el año 1808 se encargó a una delegación de la sociedad científica de Toscana comparar el Metro patrón, enviado desde París por la Comisión de pesos y medidas, con la Unidad elemental del antiguo sistema de medidas toscano.
Para comparar ambos sistemas, se consideró, pues, el tamaño del Brazo florentino en base a cero grado en el termómetro centígrado de René Antoine Ferchault de Réaumur, 1683-1757, pero, para ser exacto, en la práctica sólo se podía medir a la temperatura ambiente del material que estuviera elaborado el patrón de medida.
|
Di qui è che rimangono indubitatamente fissati per elementi di rapporto e delle Tavole annessi i tre risultati che seguono, cioè:
Metro al Braccio 1. a 0,583625839... |
|
|
Braccia |
Soldi |
Denari |
Total |
||||||
|
Metro eguale a |
= |
|
1. |
14. |
3,222 |
|||||
|
|
0,583625839 |
+ |
0,4085380873 |
+ |
0,01269386199 |
= |
1 |
0,0048577883 | ||
|
|
Metri |
Decimetri |
Centimetri |
Millimetri |
Total |
||||||
|
Braccio eguale a |
= |
|
0. |
5. |
8. |
3626. |
5,626 |
||||
|
|
0 |
+ |
0,5 |
+ |
0,080 |
+ |
0,003626 |
= |
0,583626 |
En base al criterio de las medidas que se consideraron en la Toscana hemos obtenido un error de 0,0048577883 metros en la longitud del Braccio florentino, no obstante, aplicando la lógica de la proporcionalidad hemos obtenido los siguientes resultados:
|
De manera, que, sin duda, por los tres siguientes resultados se establecen los elementos del informe en las tablas adjuntas, a saber:
Metro a Braccio 1. a 0,583333333... |
|
|
Braccia |
Soldi |
Denari |
Total |
|||||
|
Metro igual a |
= |
|
1. |
14. |
3,222 |
||||
|
|
0,583333333 |
+ |
0,408333333 |
+ |
0,007826388 |
= |
0.99949305551 |
|
|
Metri |
Decimetri |
Centimetri |
Millimetri |
Total |
||||||
|
Braccio igual a |
= |
|
0. |
5. |
8. |
3333. |
|||||
|
|
0 |
+ |
0,5 |
+ |
0,080 |
+ |
0,003333 |
= |
0,5833333 |
Pero, por otro lado, en el cambio de un sistema sexagesimal, de antiguo abolengo, por el nuevo sistema métrico, es muy improbable que no se hubiera tenido en cuenta aplicar la exacta proporción, en cuya relación matemática se compara, pues, dos o más cantidades entre sí.
De modo, que si en el primer tercio del siglo XXI una fracción del Brazo florentino es proporcional a otra del sistema métrico francés, entonces, se confirma un descubrimiento para que a partir de ahora cualquier idea plástica de la escuela florentina clásica se pueda medir con justa razón.
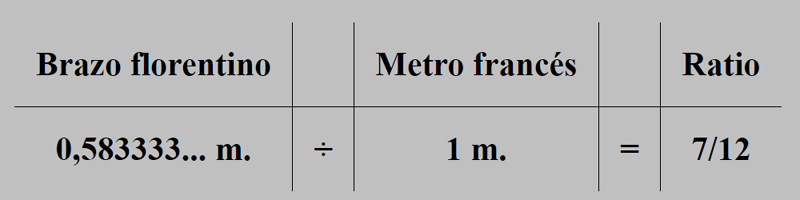
Matemáticamente, la longitud del patrón de medidas florentino es divisor de 1 metro francés, ya que su tamaño corresponde a 7/12 de metro, por lo que no hay duda de que ya existía un patrón de medida de 100 centímetros de longitud desde tiempos remotos, que, a lo largo de la historia, nadie supo de su existencia, sin embargo, fue el fundamento del tamaño del Brazo florentino.
| COMPARACIÓN DE SISTEMAS DE MEDIDAS | EQUIVALENCIAS | |||||||
| UNIDAD | MILÍMETROS | VALOR EXACTO | Brazo florentino | Metro francés | ||||
| EL METRO FRANCÉS | 1000 | = | 1000 | 12/7 | ||||
| BRAZO FLORENTINO | 0,583333... | = | 1750/3 | 7/12 | ||||
|
|
Y no hablamos, pues, de que si el huevo vino antes que la gallina, sino, que se dice, que el metro centesimal corresponde a la diezmillonésima parte del arco de meridiano que va del polo Norte al Ecuador.
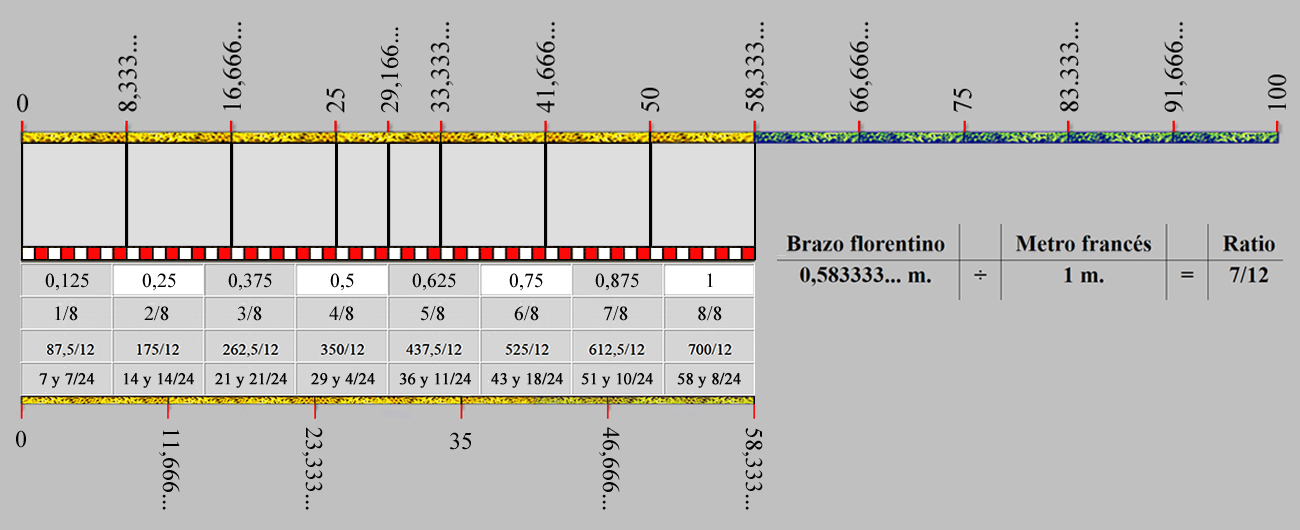
|
|
Volvamos, pues, a Florencia, y continuemos con el estudio de las subdivisiones del Brazo Florentino, pero, antes de continuar, mostraremos la relación áurea, en base al número Phi, entre el Brazo florentino y el metro francés:
100 cm. - 39,7 cm. = 60,3 cm. que le corresponde 1/2 + √5/2 = Φ
|
|
|
|
|
|
El Hombre de Vitrubio
Leonardo da Vinci diseña este
conocido dibujo en una hoja de papel del siguiente modo:
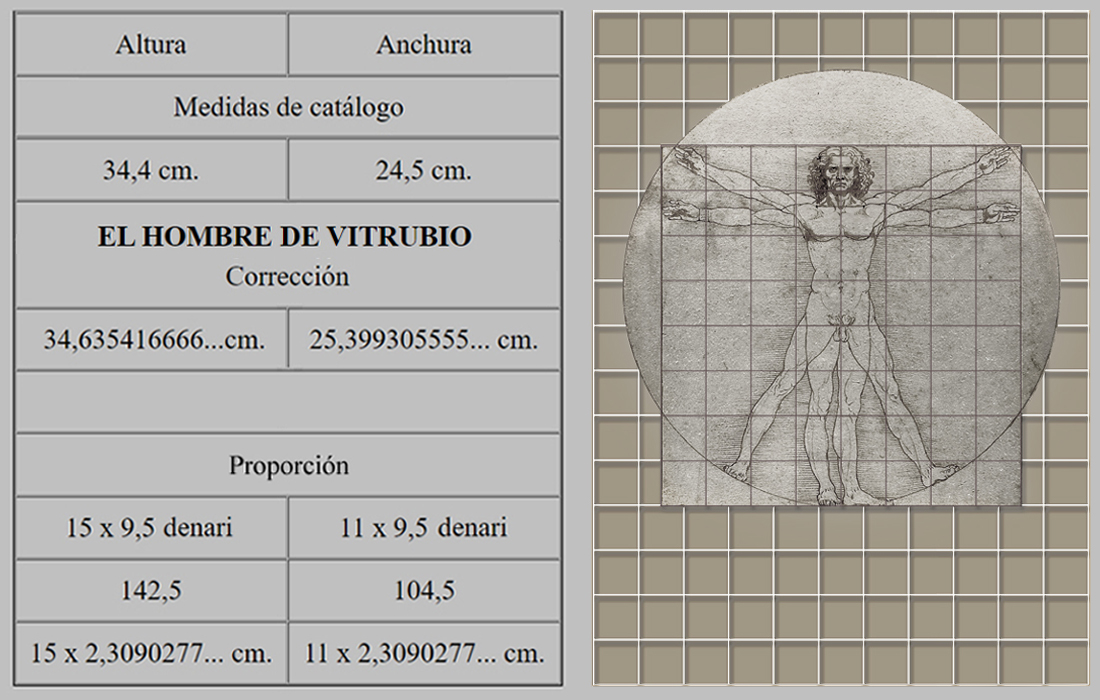 |
Para averiguar el tamaño de la cuadrícula geométrica empleada por Leonardo da Vinci en el dibujo del Hombre de Vitrubio, hemos utilizado el denaro florentino, que equivale a 0,243055... cm., de modo, que esta cuadrícula está compuesta por 15 × 11 cuadrados de 9,5 denari, que miden de lado cada uno 2,3090277... cm.
|
|
|
|
Y al mismo tiempo, pues, se observa que la altura y anchura del Hombre de Vitrubio está inscrita, a su vez, en un cuadrado de 8 subcuadrados de lado, que mide cada uno 9,5 denari de lado, y que hacen un total de 76 denari.
Luego la altura real en el dibujo sería:
76 denari × 0,2430555... cm. por denaro = 18,472222... cm.
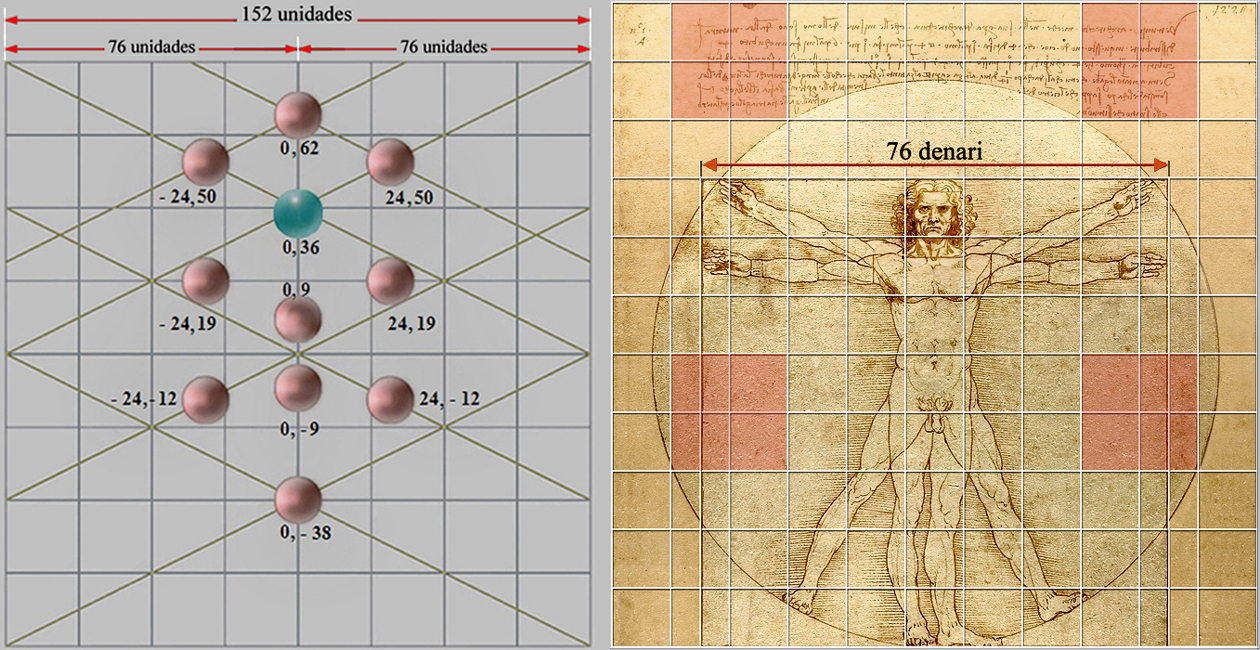 |
|
|
No obstante, en el lado del cuadrado, que inscribe la altura y anchura del Hombre de Vitrubio, se aplica el número 76, nos referimos, pues, a una cifra divisora contenida dos veces en el tamaño del lado de la cuadrícula de trabajo de 8 × 8 cuadrados que utilizamos para el estudio de Las Meninas, cuyos lados, en el ejemplo del dibujo de Leonardo da Vinci del año 1492, miden 9,5 denari, lo que multiplicado por 8 sumaría un total de 76 denari florentinos.
Y suponiendo que la cuadrícula de trabajo, que inscribe la altura y anchura del Hombre de Vitrubio, represente a escala 3 brazos, entonces, en el mundo real, su altura correspondería al siguiente resultado:
Operación: 3 brazos de 58,333333... cm. es igual a 175 cm., y, a su vez, cada subcuadrado mediría 175 cm. entre 8, que es igual a 21,875 cm., que representan, pues, 90 denaro.
| cuadrados | valor del cuadrado | centímetros | brazos | denaro | ||||
| 8 | × | 21,875 cm. | = | 175 | = | 3 | = | 720 |
/
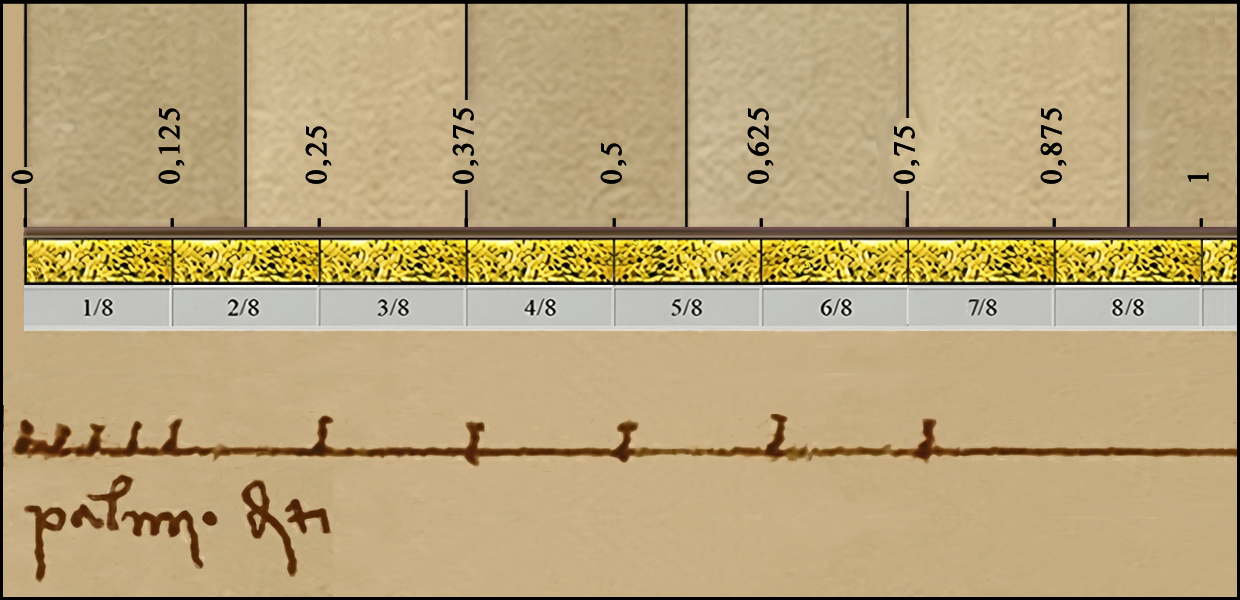 |
|
|
El David de Miguel Ángel
Esta escultura representa el momento previo en el que el
futuro rey David, padre de Salomón, se va a enfrentar con el gigante Goliat, y
simboliza, pues, la fortaleza de la República de Florencia ante sus derrocados
dirigentes, los Médici, además de la cautela ante la amenaza de los estados adyacentes,
principalmente los Estados Pontificios.
El David fue labrada en mármol blanco por Miguel Ángel Buonarroti con 26 años entre el 1501 al 1504, y mide 5,17 metros de altura.
| centímetros | 516,9791666... |
 |
||
| braccios | 8,8625 | |||
| codos | 14,770833... | |||
| 1/2 braccio | 17,725 | |||
| soldi | 177,25 | |||
| quattrini | 531,75 | |||
| denari | 2127 | |||
| punti | 25524 | |||
|
Galería de la Academia. Florencia |
En esta propuesta se demuestra la diferencia entre medir con el Brazo Florentino y el metro decimal francés.
Veamos, en la ficha técnica de la escultura del David se dice que mide 517 centímetros de altura, pero, como se puede comprobar en medidas florentinas, el David de Miguel Ángel Buonarroti, le corresponderían, pues, 2127 denari.
2127 denari × 0,243055... centímetros por denaro = 516,979166... centímetros.
517 centímetros equivaldrían, exactamente, a 2127,085714286... denari.
Diego Velázquez
El caballo blanco, en
posición de corveta, con los cuartos traseros en tierra y las manos levantadas
en el aire, es un estudio preparatorio para el retrato ecuestre del primer
ministro, el conde duque de Olivares.
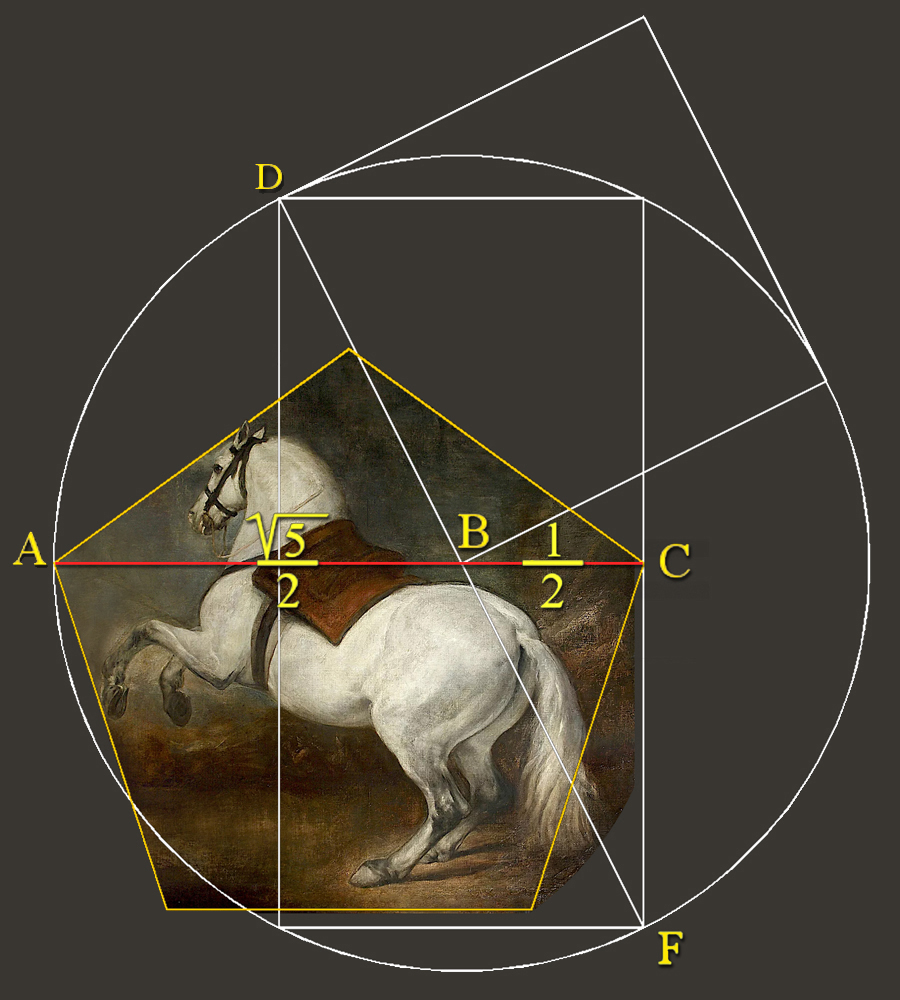 |
|
1636
Palacio Real de Madrid
310 × 246 cm.
150 × 120 unidades |
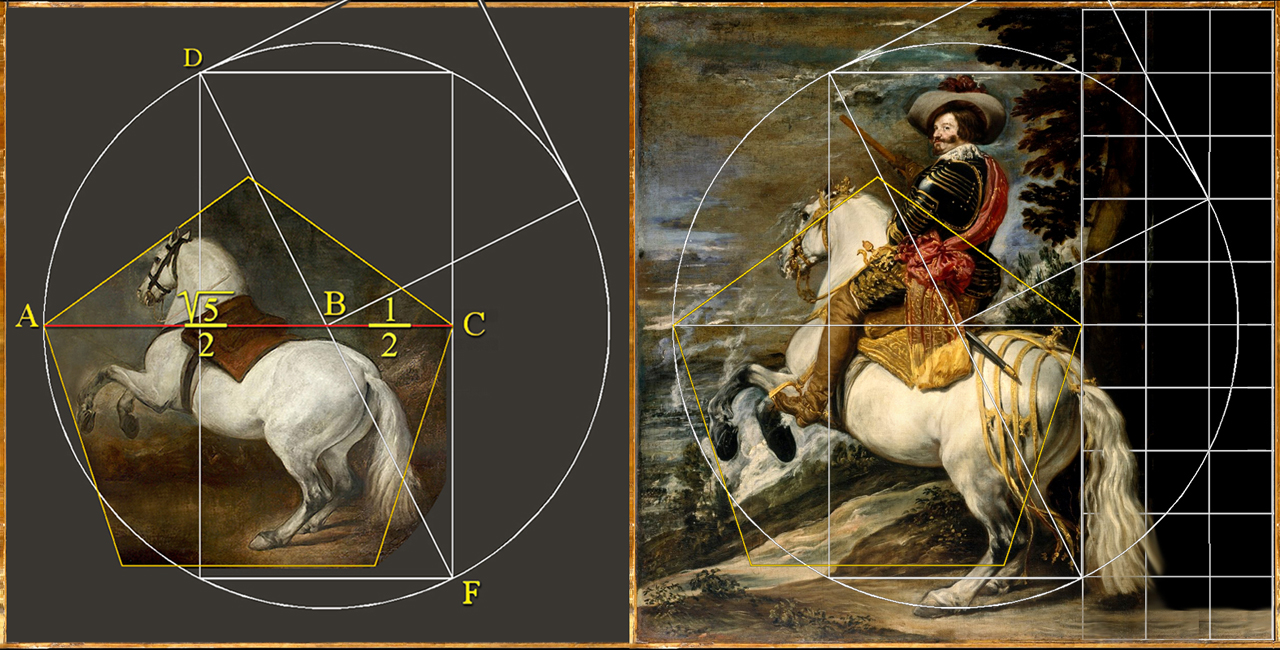 |
 |
|
1636
Metropolitan Museum of New York |
El Greco
Detalle de la Coronación de la Virgen María.
 |
|
1592
Museo del Prado. Madrid |
notas a pie de página
1 - Página 37 - Luca Pacioli - La Divina proporción - Ediciones Akal, S. A. - 1991. Del manuscrito existente en la Biblioteca Ambrosiana de Milán dedicado al Duque de Milán Ludovico il Moro. Traducción de Juan Calatrava.
2 - THE POLEMIC PROBLEM: What is the value of Pi. Gould, S. C. (Sylvester Clark). Publisher Manchester, N.H. 1888.
3 - Breve ayuda del desarrollo del valor del número áureo Phi - Φ.
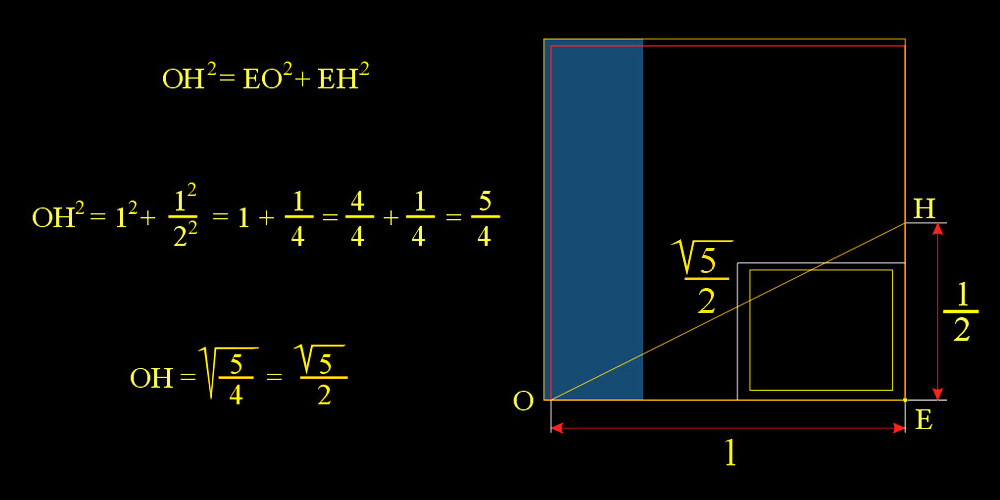 |
|
Análisis matemático geométrico |
4 - M. Loeffler, Le symbolisme des contes de Fées. París, 1949.
5 - El Sefer Yetzirah es el tratado más antiguo del mundo contemplativo hebreo.
|
|
זה השׁער ליהוה צדיקים יבאו בו׃ Esta es la puerta de Jehovah por ella entrarán los justos. Salmo 118:20
Editio princeps del Sefer Yetzirah
ספר יצירה
Libro de la Creación
Mantua 1562 - Editado por Jacob ben Naftali Gazolo |
De acuerdo a Ithamar Gruenwald hay tres primeras versiones del Sefer Yetzirah o Libro de la Creación; una corta, otra larga de algo menos de 2500 palabras y la llamada versión Saadia con comentarios del temprano siglo X.
El Sefer Yetzirah, igual que el libro de la Torah, empieza por la misma letra; por la letra Bet.
Las dos primeras palabras del relato bíblico de la creación:
Berashit bara.
Estas dos letras Bet hacen alusión al misterio de la Creación cuya viva doctrina se desarrolla en el Sefer Yetzirah.
בראשׁית ברא
|
בשלשים ושתים נתיבות פליאות חכמה חקק יה יהוה צבאות אלהי ישראל אלהים חיים ומלך עולם אל שדי רחום וחנון רם ונשא שוכן עד וקדוש שמו מרום וקדוש הוא וברא את עולמו בשלשה ספרים בספר וספר וספור׃ |
1:1 / Con treinta y dos senderos prodigiosos de Sabiduría grabó Yah, el Señor de los Ejércitos, el Dios de Israel, Elohym vivo, Rey del mundo, el Shaddai Misericordioso y Clemente, Elevado y Supremo, que reside en la Eternidad y su nombre es Santo. Y creó Su mundo con tres libros;
|
|
עשר ספירות בלי מה ועשרים ושתים אותיות יסוד שלש מאות ושבע כפולות ושתים עשרה פשוטות׃ |
1:2 / Diez Sefirot en el vacío y veintidós letras de Fundamento: Tres Madres, Siete Dobles y Doce Simples. |
|
עשר ספירות בלימה במספר עשר אצבעות חמש כנגד חמש וברית יחיד מכוון באמצע במילת הלשון ובמילת המעור׃ |
1:3 / Diez Sefirot en el vacío: Ordenadas como el número de los diez dedos. Cinco frente a cinco, y la Alianza del Único orientada hacia el centro, como la circuncisión de la lengua y la circuncisión del miembro. |
|
עשר ספירות בלימה עשר ולא תשע עשר ולא אחת עשרה הבן בחכמה וחכם בבינה בחון בהם וחקור מהם והעמד דבר על בוריו והשב יוצר על מכונו׃ |
1:4 / Diez Sefirot en el vacío: Diez y no nueve, diez y no once. Entiende por la Sabiduría y penetra con Inteligencia. Distingue con ellas y escruta desde ellas. Haz que cada cosa se yerga sobre su evidencia y haz que el Formador se siente sobre Su base. |
|
עשר ספירות בלימה מדתן עשר שאין להם סוף עומק ראשית ועומק אחרית עומק טוב ועומק רע עומק רום ועומק תחת עומק מזרח ועומק מערב עומק צפון ועומק דרום אדון יחיד אל מלך נאמן מושל בכולם ממעון קדשו עד עדי עד׃ |
1:5 / Diez Sefirot en el vacío: Su medida es diez que no tienen fin. La profundidad del principio, la profundidad del fin, la profundidad del bien, la profundidad del mal, la profundidad de arriba, la profundidad de abajo, la profundidad del este, la profundidad del oeste, la profundidad del norte, la profundidad del sur. El Maestro único. Dios, Rey fiel, domina sobre todas ellas desde su Santa Morada hasta la Eternidad de las Eternidades. |
|
עשר ספירות בלי מה צפייתן כמראה הבזק ותכליתן אין להם קץ ודברו בהן ברצוא ושוב ולמאמרו כסופה ירדופו ולפני כסאו הם משתחוים׃ |
1:6 / Diez Sefirot en el vacío: Su percepción es como la aparición del relámpago, su límite no tiene fin. Su Verbo se encuentra en ellas, realizando un rápido e incesante movimiento de ida y vuelta. Y su palabra ellas persiguen como en un torbellino, y ante su Trono le rinden alabanzas. |
|
עשר ספירות בלימה נעוץ סופן בתחלתן ותחלתן בסופן כשלהבת קשורה בגחלת שאדון יחיד ואין לו שני ולפני אחד מה אתה סופר׃ |
1:7 / Diez Sefirot en el vacío: Su fin penetra en su principio, y su principio en su fin, como la llama ligada a la brasa. Pues el Maestro es único y no hay quien le sea segundo, y antes del Uno; ¿qué podrías tu contar? |
|
עשר ספירות בלימה בלום פיך מלדבר ולבך מלהרהר ואם רץ פיך לדבר ולבך להרהר שוב למקום שלכך נאמר יחזקאל א') והחיות רצוא ושוב ועל דבר זה נכרת ברית׃) |
1:8 / Diez Sefirot en el vacío: Refrena tu boca de hablar, y tu corazón de meditar. Y si tu corazón se precipitara regresa al lugar. Por eso está escrito: Las Chayot corrían y retornaban. Y sobre esto tuvo lugar una Alianza. |
|
|
La fecha de composición de este texto es causa de debate; la mayoría de los entendidos están de acuerdo en que fue escrito o compilado entre el siglo II y VI.
Sin embargo, Steven M. Wasserstrom ha señalado de una clara transición islámica en el siglo IX, aunque es del todo seguro que ejerció una gran influencia especulativa y mística durante el siglo X.
El comentario de Elliot R. Wolfson remarca:
Propiamente hablando, este trabajo no debería ser definido como una simple composición, y más que nada porque es una composición elaborada a partir de distintas y legendarias literaturas, que han permanecido juntas y enraizadas a través de un complicado proceso de redacción, cuyas etapas no son discernibles.
La mayoría de la versiones del Sefer Yetzirah se componen de seis capítulos cortos de lacónicas declaraciones, similar al tono de los textos Hekhalot o de los tempranos del misticismo del Carro.
Para comprender la importancia de este texto habría que tener bien presente que la Kabala extrajo de su primer capítulo la palabra Sefirot y la noción del estado metafísico de la creación.
Sefer Yetzirah - El Libro de la Creación. Teoría y Práctica, razonado y explicado por Aryeh Kaplan. Editorial Mirach, S. L., 1994.
Título en inglés: Sefer Yetzirah. The Book of Creation. Publicado por acuerdo con Samuel Weiser, Inc. 1990.
6 - Página 349 - I DIECI LIBRI DELL´ARCHITETTURA DI M. VITRVVIO. Tradotti & commentati da Monſ. Daniel Barbaro eletto Patriarca d´Aquileia, da lui riueduti & amplati; & hora in piu commoda forma ridotti. In Venetia, MDLXVII.
Libro IX – Cap. II.
Della ſquadra inuentione di Pitagora per formare l´angulo giusto.
Pitagora ſimilmente dimoſtrò la ſquadra ritrouata ſenza opera di artefice alcuno, & fece chiato con quanto grande fatica i fabri facendola, a pena la poſſono al giuſto ridurre. Queſta coſta con ragioni, & uie emendata, da ſuoi precetti ſi manifeſta: perque ſe egli ſi prenderà tre regole, una di piedi tre, l´altra di quattro, la terza di cinque, & queſte regole compoſte ſiano, che con i capi ſi tocchino inſieme facendo una figura triangulare, condurranno la ſquadra giuſta.
7 - Página 86 - DISCVRSO XCIIII. DE LOS ARQUITECTOS EN vniverſal, Fortificadores de Fuerças, y maeſtros de maquinas, o Ingenieros. Plaza Vniuersal de todas Ciencias y Artes - Christoval Suarez de Figueroa - Madrid. 1615.
8 - Dando al Do el valor de 1 se establece la tabla de frecuencias de afinación.
9 - Diagrama cartesiano
El plano se divide en cuatro partes llamadas cuadrantes mediante dos rectas perpendiculares entre sí, la horizontal y la vertical respectivamente.
Dichas rectas se cortan en un punto que recibe el nombre de origen de coordenadas; cuya posición es la coordenada (0,0).
Las rectas se dividen en segmentos de igual longitud y a cada marca del segmento se le asigna un número entero.
En la recta horizontal, llamada eje de abscisas o eje de las x, al punto de corte con la otra recta se le asigna el 0 y hacia la derecha el 1, 2,..., y hacia la izquierda el -1, -2,... y así sucesivamente en ambas direcciones.
De forma análoga se procede con la recta vertical, llamada eje de ordenadas o eje de las y, al punto de corte con la otra recta se le asigna el 0 y hacia arriba el 1,2,...., y hacia abajo el -1,-2,... y así sucesivamente en ambas direcciones.
De modo que tenemos la situación del dibujo.
|
|
Así pues, cada punto del plano se localiza mediante dos números correspondientes a cada eje, que se escriben encerrados entre paréntesis y separados por una coma (,).
Dicho par de números se llaman coordenadas.
Y se obtienen, por ejemplo, de la siguiente manera:
El punto de coordenadas (2,3) se localiza situándonos en el punto marcado con el 2 en el eje de las “x”; una vez aquí, subimos paralelamente al eje de las “y”, hasta el lugar marcado en este eje con el 3.
De igual forma para el punto (-3,2), nos situamos en la marca -3 del eje “x” y subimos verticalmente hasta el 2 del eje “y”.
10 - PROLUSIONES CHRONO EMBLEMATICÆ IN MORTEM Auguſtiſsimæ Imperatricis MARGARITÆ. IOANNES FRANCISCVS CHRISTOPHORVS - BARON TALMBERG. PRAGÆ. 1673.
11 - Será en el año 1843, en el catálogo del Museo del Prado redactado por Pedro de Madrazo, cuando esta pintura aparezca mencionada por primera vez como Las Meninas.
12 - Página 333 - Libro Tercero. De la Casa Real y sus oficios. Teatro de las Grandezas de la Villa de Madrid. Corte de los Reyes Catolicos de Eſpaña. Al muy poderoso Señor Rey Don Felipe Qvarto. Por el Maestro Gil Gonzalez Davila. 1623. Madrid.
13 - El ajedrez siempre estuvo vinculado a la Geometría y Matemática, y por supuesto, a la Guerra.
Comenta Ruy López de Segura, a quien se le considera como el primer campeón de ajedrez registrado en Europa, que dedicó su libro a don García de Toledo, ayo y mayordomo mayor del Príncipe heredero don Carlos:
|
Ser el iuevo del axedrez juego de ſciencia, è inuencion mathematica, conſta por muchas coſas. La primera, porque el eſta fundado ſobre dos artes liberales, couiene a ſaber, Geometria y Arithmetica: porque es notorio eſtar compueſto ſobre vn lado de ſuperficie quadrada y plana, y perficionado con numero de ocho, que es numero pleno, ſegun que es notorio a todos los que algo ſaben: el qual multiplicado en ſi meſmo cria vna multiplicacion, è numero de ſeſſenta y quatro. |
|
|
14 - Dictionnaire des Symboles. JEAN CHEVALIER - ALAIN GHEERBRANT. Paris. 1990.
15 - Página 22 - The Cross of the Magi. The true Mosaic Pavement of sixty four squares. Frank C. Higgins. New York. 1912.
16 - Página 158 - KIRCHER - ARITMOLOGIA - Historia real y esotérica de los números - Traducción, de la edición del año MDCLXV, Romæ, del latín de Atilano Martínez Tome. Editorial Breogan. Madrid, 1984.
17 - Por fortuna, fue en la página nº 13, de un libro editado en 1642 en Ámsterdam, donde finalmente se produjo el anhelado reencuentro entre Las Meninas de Diego Velázquez y la Kabala:
El Sefer Yetzirah comentado en hebreo por Yosef ben Shalom Ashkenazi, y traducido al latín por Joanne Stephano Rittangelio.
 |
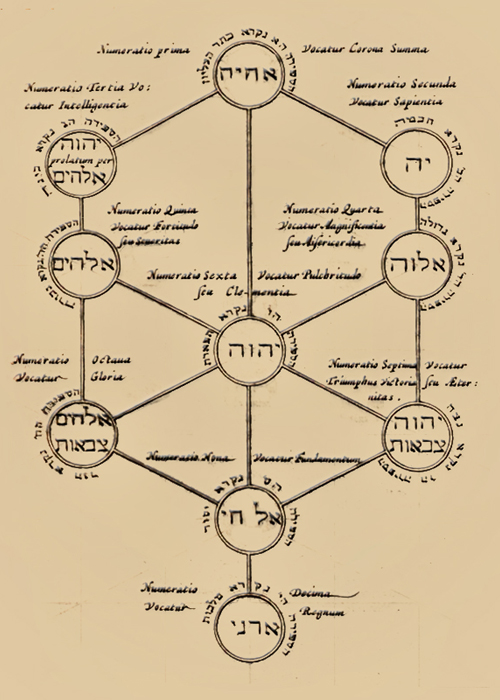 |
|
Sefer Yetzirah - Joanne Stephano Rittangelio - Ámsterdam
1642 |
18 - Boletín del Museo del Prado. Mayo-agosto 1984. La restauración de Las Meninas de Velázquez. Manuela B. Mena Marqués.
19 - Ramiro Moya: El trazado regulador y la perspectiva en Las Meninas.
REVISTA ARQUITECTURA.
ÓRGANO DEL COLEGIO OFICIAL DE ARQUITECTOS DE MADRID.
AÑO 3 NUM. 25 - ENERO 1961.
|
|
|
|
20 - Página 379 - LA LIBRERÍA DE VELÁZQUEZ. F. J. SÁNCHEZ CANTÓN. HOMENAJE OFRECIDO A MENÉNDEZ PIDAL
Miscelánea de estudios lingüísticos, literarios e históricos. Tomo tercero. Madrid. 1925.
21 - El inventario de la librería de Velázquez constituye una manifestación elocuente de su particular gusto frente a lo que era común en su tiempo en la educación de un pintor.
En su biblioteca, de algo más de 150 volúmenes, encontramos, sobretodo, temas relacionados con la Aritmética, Geometría y Arquitectura.
|
· 415. - Antonio Buscon, De Architectura italiano. · 417. - De fortificacion cat. Yomo Castrioro. · 419. - Vitrubio de Arquitectura. · 420. - Matemática de Aguilon. · 421. - Galasso Matematica en dos tomos. · 422. - Architectura de Vicencio Escamacio beneciano. · 423. - Alberto Durero, Simetria italiano. · 424. - Cataneo de Architectura italiano. · 425. - Jeometria de Bitelono. · 427. - Architectura de Leon Alberti. · 428. - Sebastian Serlio, Architectura. · 433. - Vitrubio, Architectura. · 440. - Geometría práctica. · 448. - Elementos de Euclides. · 450. - Matemática de Pedro Cataneo. · 461. - Perspectivas de Euclides. |
· 462. - Perspectivas de Daniel Barvaro. · 463. - Arismetica de Moya. · 464. - Vitruvio de Architectura. · 466. - Serguio, De Architectura. · 467. - Numeros y medidas. · 468. - Nicolao Tartalia en italiano. · 469. - Vitruvio, Architectura en italiano. · 470. - Juan Antonio Buscon, Architectura. · 478. - André Palladio de Architectura. · 480. - Algebra de Pedro Nuñez. · 490. - Especularia, en italiano. · 491. - Marco Aurelio Alemán. Arismetica. · 493. - Céspedes de Geometría. · 497. - División de superficies, italiano. · 498. - Summa Astrológica. · 503. - Perspectiva de Euclides. |
· 507. - Aritmetica de Joseph Unicornio, italiano. · 508. - Baptista Alberto, italiano. · 511. - Euclides filósofo. · 516. - Antonio Fineo, Aritmética. · 519. - Materia de Architectura. · 532. - Practica de perspectiva, italiano. · 533. - Jacomo Barrocio de Architectura. · 536. - Serlio de Architectura. · 538. - Pedro Cataneo de Architectura. · 545. - Sciencia Matematicas de Nejarense. · 551. - Mobimiento de los planetas. · 553. - Antonio Labaco, Architectura. · 554. - Alberto Durero, Geometría. · 556. - Architectura de Vitrubio, italiano. · 558. - Leonardo de Vinci, de la pintura. · 561. - Pedro Antonio Darca de Architectura. |
|
Los ejes fundamentales que sostienen la estructura temática de la biblioteca velazqueña son, como ha sido señalado, la geometría y perspectiva, la cosmografía y la arquitectura. Y por ello por el número de ejemplares de cada materia que podemos catalogar, pero también por la importancia cualitativa y el carácter enciclopédico con que se articulan todas estas disciplinas a partir de la ciencia del número, lo que manifiesta la organicidad de la concepción intelectual de nuestro pintor. La relación de estas ciencias con el conjunto del quadrivium es directa y evidente. (...). |
Página 23, Catálogo de Pedro Ruiz Pérez: De la Pintura y las Letras. La Biblioteca de Velázquez, editado por: E. P. G. Conserjería de Cultura. Junta de Andalucía. 1999.
22 - La obra de Euclides ha resistido el paso del tiempo, como ninguna otra científica a lo largo de más de 2300 años, y es casi seguro que la traducción de Rodrigo Zamorano fuera la que se usara en el aprendizaje pictórico de la escuela de Francisco Pacheco, el maestro de Velázquez.
Rodrigo Zamorano, nace en Valladolid, 1542, y muere en Sevilla, 1620, se le considera uno de los mayores sabios y científico en la época de Felipe II.
Tradujo la primera edición en castellano de los Elementos de Euclides; la obra cumbre del lenguaje geométrico de toda la Matemática elemental griega: Geometría plana y espacial, Aritmética y Álgebra.
Libro VI - Definición 3
Dizeſe ſer diuidida vna linea recta con razon extrema y media quando fuere que como ſe ha toda a la mayor parte, aſſi la mayor a la menor.
Libro II - Problema 1 - Proposición 11
Diudir una linea de manera que el rectangulo de toda ella y vna de ſus partes ſea ygual a aquel quadrado que ſe haze de la parte que resta.
LOS SEIS LIBROS PRIMEROS DE LA GEOMETRIA DE EVCLIDES - Traduzidos en lengua Eſpañola por Rodrigo Çamorano Aſtrologo y Mathematico, y Cathedratico de Coſmografia por ſu Mageſtad en la caſa de la Contratacion de Seuilla. Dirigidos al illuſtre ſeñor Luciano de Negron, Canonigo de la ſancta ygleſia de Seuilla. Con licencia del Conſejo Real. En Seuilla en caſa de Alonſo de la Barrera. 1576.
23 - Ya hemos comentado que 1,125 unidades por pulgada equivale a 23,25 milímetros; y es, por tanto, el número que traduce matemática y geométricamente la pulgada castellana al sistema métrico.
Básicamente, este número nos pone en contacto directo con realidad, profundidad y exactitud con el engranaje geométrico de este lienzo.
|
En la siguiente tabla se plasma el descubrimiento del valor de la pulgada castellana convertida a unidades; lo cual indica que nos hallamos ante la cuantía de 1,125 unidades por pulgada, o número roseta, que traduce las pulgadas castellanas en cualquier clase de sistema de medidas longitudinales, y que, con extrema exactitud, también nos pone en contacto con las dimensiones reales de Las Meninas. |
| 9 partes | Unidades | La Pulgada en 9 partes | Pulgadas | Milímetros | ||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 |
| 8/8 | = | 1 | 8/9 | = | 0,888888 | 20,666666 |
| 7/8 | = | 0,875 | 7/9 | = | 0,777777 | 18,083333 |
| 6/8 | = | 0,75 | 6/9 | = | 0,666666 | 15,5 |
| 5/8 | = | 0,625 | 5/9 | = | 0,555555 | 12,916666 |
| 4/8 | = | 0,5 | 4/9 | = | 0,444444 | 10,333333 |
| 3/8 | = | 0,375 | 3/9 | = | 0,333333 | 7,75 |
| 2/8 | = | 0,25 | 2/9 | = | 0,222222 | 5,166666 |
| 1/8 | = | 0,125 | 1/9 | = | 0,111111 | 2,583333 |
|
|
1,125 unidades por pulgada × 0,888.888 pulgadas por unidad = 1.
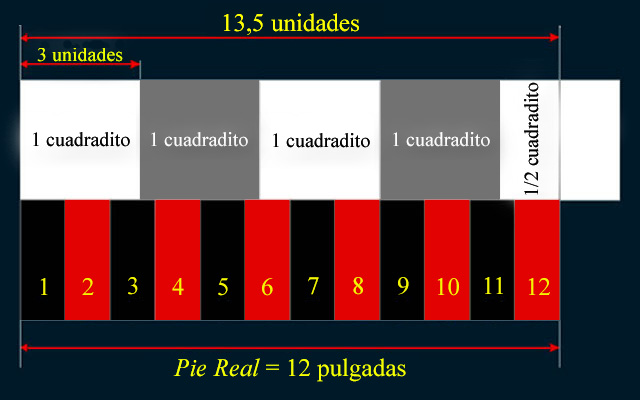 |
|
El Pie Real equivale a 13,5 unidades en la rejilla de trabajo. |
Si una pulgada equivale a 1,125 unidades
en la cuadrícula de trabajo, entonces; sólo hay que multiplicar 1,125
unidades
por 12 para obtener 13,5 unidades, que es la cantidad que representa en esta
misma cuadrícula 4,5 cuadraditos valiendo el Pie Real 12 pulgadas.
24 - En la página 46, CAPITULO VIII, Luca Pacioli escribe, a finales del siglo XV, que estas partes irracionales así descritas en el arte se llaman residuos.
Luca Pacioli - La Divina proporción - Ediciones Akal, S. A. - 1991. Del manuscrito de la Biblioteca Ambrosiana de Milán dedicado al Duque de Milán Ludovico il Moro. Traducción de Juan Calatrava.
El tamaño del error de 2,7192983 mm. nos sitúa en el lugar del observador meticuloso, ya que hay varias ideas en juego en la concepción de este error:
Euclides es el autor de esta Proposición 11, lo cual la hace inalterable.
El segmento ITXK mide 94 unidades + 152 unidades = 246 unidades.
246 unidades equivalen a 23,25 mm por pulgada × 246 unidades / 1,125 unidades por pulgada = 5084 mm. = 5,084 metros.
El error de trazado sería una recta perpendicular de 2,7192983 milímetros de ancho por 5,084 metros de largo.
Nuestra opinión; el grosor de un simple carboncillo generaría un error aún mayor.
|
Cuadrículas |
Valor - AB |
Valor - TB | Valor - AT |
AT / TB = Φ |
|
Línea de acotación |
144 |
54 | 90 |
90/54 = 1,666666666 |
|
Límite de la rejilla de 150 unidades |
150 |
57 | 93 |
93/57 = 1,631578947 |
|
Límite de la rejilla de 152 unidades |
152 |
58 | 94 |
94/58 = 1,620689655 * |
|
Phi - Φ |
1,618033988... |
|||
|
153 / 1,125 = 136 pulgadas |
153 |
58,5 | 94,5 |
94,5/58,5 = 1,615384615 ** |
|
Borde del orillo del lino original |
155,25 |
59,625 | 95,625 |
95,625/59,625 = 1,603773585 |
|
|
* - Desplazado respecto al punto de fuga hacia la derecha 2,7192983 mm.
** - Desplazado respecto al punto de fuga hacia la izquierda 2,735294093 mm.
|
|
|
|
25 - La obra denominada: Movimiento de los planetas de Nicolás Copérnico se hallaba en la biblioteca personal de Velázquez; un libro proscrito por la ortodoxia católica, cuyo mensaje innovador corre en paralelo con el espíritu presente en la pintura del artista sevillano.
Nicolás Copérnico, 1473 - 1543, fue un astrónomo del Renacimiento que formuló la teoría heliocéntrica del Sistema Solar, concebida en primera instancia por Aristarco de Samos.
El científico polaco pasó cerca de veinticinco años trabajando en el desarrollo de su modelo heliocéntrico del universo, y lo publicó en su libro De revolutionibus orbium coelestium, y en castellano Sobre las revoluciones de las esferas celestes, que resultó ser una teoría demasiado revolucionaria para que fuera aceptada por los científicos de la época.
Copérnico es considerado el pionero de la astronomía moderna, además de ser una pieza clave a lo que se llamó la Revolución Científica.
En De revolutionibus orbium coelestium explica su teoría heliocéntrica, basado en la Geometría de Euclides, a partir de seis teoremas y un problema.
En el Libro I, Teorema I, demuestra, en base al diámetro de un círculo, las medidas de los lados del triángulo, tetrágono, cuadrado, hexágono, pentágono y decágono, a los que circunscribe dicho círculo, donde desarrolla el valor del número áureo Phi.
|
Cálculo de la proporción áurea por Nicolás Copérnico
|
Theorema primum. Dato circuli diametro, latera quoque trigoni, tetragoni, hexagoni, pentagoni, & decagoni dari, quæ idem circulus circumſcribit. Quoniam quæ ex centro, dimidia diametri æqualis eſt lateri hexagoni. Trianguli uero latus triplum, quadrati duplu m poteſt eo quod ab hexagoni latere ſit quadratum, prout apud Euclidem in elementis demonſtrata ſunt. Dantur ergo longitudine hexagoni latus partium 100000. tetragoni partium 141422. trigoni partium 173205. Sit autem latus hexagoni AB, quod per XI. ſecundi, ſive XXX. ſexti Euclidis, media & extrema ratione fecetur in C ſigno, & maius ſegmentum ſit CB, cui æqualis apponat BD. Erit igitur & tota ABD extrema & media ratione diſſecta, & minus ſegmentum appoſita, decagoni latus inſcripti circulo, cui AB fuerit hexagoni latus. quod ex quinta & nona XIII. Euclidis libri ſit manifeſtum. Ipsa uero BD dabitur hoc modo fecetur AB bifariam in E: Patet per tertiam eiuſdem libri Euclidis, quod EBD quintuplum poteſt eius quod ex EB. Sed EB datur longitudine partium 50000. a qua datur potentia quintuplum, & ipsa EBD longitudine partium 111803. quibus si 50000 auferantur ipſius EB, remanet BD partium 61803 latus decagoni quæſitum. Latus quoque pentagoni, quod poteſt hexagoni latus ſimul & decagoni datur partium 117557. Dato ergo circuli diametro, dantur latera trigoni, tetragoni, pentagoni, hexagoni, & decagoni eidem circulo inscriptibilium, quod erat demonstrandum.
Teorema Primero. Dado el diámetro de un círculo, se dan también los lados del triángulo, cuadrado, hexágono, pentágono y decágono, a los que circunscribe dicho círculo. Puesto que la distancia desde el centro, el radio, la mitad del diámetro, es igual al lado del hexágono, el lado del triángulo al cuadrado es igual al triple del lado del hexágono al cuadrado, y el cuadrado del lado del tetrágono es igual al doble del lado del hexágono al cuadrado, según se demostró en los Elementos de Euclides. Luego se dan, el lado del hexágono en longitud de 100000 unidades, el del tetrágono de 141422 unidades (√2), y el del triángulo de 173205 unidades (√3). Sea. ahora, AB el lado del hexágono, que por el problema I del libro II o por el X del libro VI de Euclides, en media y extrema proporción se corta en el punto C, y sea el segmento mayor CB, igual al cual se le añade BD. En consecuencia, ABD completa estará dividida en extrema y media proporción: y el segmento menor, el añadido BD, el lado del decágono inscrito en el círculo, AB el lado del hexágono; lo cual se clarificó a partir del V y IX preceptos del libro XIII de Euclides. Pero BD se conocerá de este modo: córtese en dos partes AB en el punto E. Es patente por el III precepto del mismo libro de Euclides, que el cuadrado de EBD es igual al quíntuplo del cuadrado de EB. Pero EB se conoce con una longitud de 50000 unidades, a partir de ella se conoce el quíntuplo de su cuadrado, y EBD con una longitud de 111803 unidades (√5/2), de las cuales, si se restan 50000 que tiene EB, queda BD de 61803 (1/Φ), lado del decágono buscado. También se conoce el lado del pentágono, el cuadrado del cual es igual a la suma de los cuadrados del lado del hexágono y del decágono, de 117557 unidades:
Luego, dado el diámetro del círculo, se conocen los lados del triángulo, tetrágono, pentágono, hexágono y decágono inscritos en el mismo círculo. Que es lo que había que demostrar. |
Página - 12. Libro I. Theorema I. De revolutionibus orbium coelestium, Libri VI. Nicolai Copernici Torinensis. Norimbergae. 1543.
26 - Página - 21. EPISTOLÆ. Ad Joannem Keplerum scriptæ. Epistola X. Michæl Maestlinus - Joanni Keplero. Año 1597.
27 - Libro I - Theorema. 33. - Propoſitio. 47.
En los triangulos rectangulos el quadrado que es hecho de el lado que eſta opueſto al angulo recto es ygual a los dos quadrados que ſon hechos de los lados que contienen el angulo recto.
|
|
Sea el triangulo rectangulo .ABC. que tenga recto el angulo BAC. digo que el quadrado que es hecho del lado .EC. es ygual a los quadrados que ſe hazen de .BA. y de .AC. Deſcribaſe, por la .46. de la .BC. el quadrado .BDCE, y por la miſma, de la BA. y de la, AC. los quadrados .ABZI. ACKT. y por el punto A. tireſe .AL. parallela con la .BD. CE, por la propoſicion .31, y por la .I. peticion tireſe AD. CZ. y porque los angulos. BAC. BAI. ſon rectos. Luego tiradas dos lineas rectas .AC. AI. deſde vna linea recta .AB. y deſde vn punto en ella .A. no hacia vnas miſmas partes hacen de vna y otra parte angulos yguales a dos rectos por la .14. propoſition, luego en derecho eſta la .AC. de la .AI y por eſto tambien BA eſta en derecho de .AT y porque el angulo .DBC. es ygual al angulo .ZBA. porque cada vno dellos es recto; pongaſe comun el angulo ABC. Luego todo DBA es ygual a todo el angulo ZBC. y porque las dos .AB. BD. ſon yguales a las dos BZ. BC. la vna a la otra, y el angulo .DBA es ygual al angulo .ZBC. luego la baſis .AD, por la .4. propoſicion, es ygual a la baſis .ZC. y el triangulo .ABD. al triangulo .ZBC. es tambien igual. Y el parallelogramo .BL, por la 41, es doblo del triangulo .ABD porque tiene vna miſma baſis que es .BD. y esta en vnas miſmas parallelas, es a ſaber .DB. AL. y tambien el quadrado .IB. por la miſma, es doblo del triangulo .ZBC. porque tiene la miſma baſis que es .BZ. y eſta en vnas miſmas parallelas, es a ſaber .ZB. IC. y las coſas que ſon doblo de coſas yguales, por la .6. comun ſentencia, entre ſi ſon yguales. Luego el parallelogramo .BL. es ygual al quadrado .IB Semejantemente ſi por .I. peticion, ſe tiran .AE BK. ſe demoſtrara el parallelogramo CL. ſer ygual al quadrado .TC. Luego todo el quadrado .BDEC, es ygual a los dos quadrados .IB, TC. Y el quadrado .BDEC. es hecho de la .BC. y los quadrados IB. CT. ſon hechos de la .BA. AC. Luego el quadrado que de el lado .BC. ſe hizo es ygual a los quadrados que ſon hechos de los lados .BA. AC. luego en los triangulos rectangulos el quadrado que es hecho del lado que eſta oppueſto al angulo recto y lo que mas ſe ſigue como en el theorema, que ſe hauia de demoſtrar. |
| Demostración |
LOS SEIS LIBROS PRIMEROS DE LA GEOMETRIA DE EVCLIDES - Rodrigo Çamorano. Seuilla. 1576.
28 - El estudio de la localización del punto de fuga áureo podría ser analizado de manera diferente, veamos a continuación otra nuevas aportación.
|
|
|
|
29 - El gran invento geométrico de Brunelleschi fue divulgado por el arquitecto Alberti en su Tratado de la Pintura - 1436, y, casi cuarenta años después, Piero della Francesca, 1420-1492, sistematizó la perspectiva lineal en su libro: De Prospectiva pingendi - 1474.
De Prospectiva pingendi está considerada como una extensión del tratado de Alberti, aunque influenciada por la Óptica de Euclides y los Elementos, donde hace continuas referencias al escritor griego.
Tras la muerte de Piero della Francesca una buena parte de su trabajo escrito inspiró a notables autores de tratados de Geometría.
En el libro de Luca Pacioli De divina proportione, ilustrado por Leonardo da Vinci, los estudios de Piero, sobre los sólidos geométricos, están presentes.
Piero della Francesca es el único pintor de su época que hace uso de una Matemática sofisticada, la cual supuso el puente entre la perspectiva artística y la Geometría.
La perspectiva lineal, nacida de la observación, estaba en contradicción con los postulados geométricos admitidos en en el siglo XV.
En efecto; en la Geometría de Euclides las paralelas son siempre equidistantes, y por mucho que se las prolonguen nunca se encuentran en un sólo punto; pero en la Geometría no euclidiana, generada de la experiencia del campo visual, aquel postulado se revelaba falso, pues, como demostró Filippo Brunelleschi, en el punto de fuga convergen todas las paralelas a la altura del nivel de ojo u horizonte.
30 - No obstante, nos hemos basado en dos ideas complementarias que responden a la génesis geométrica de Las Meninas:
Una la del Teorema de Tales de Mileto, que afirma que cualquier ángulo inscrito en un semicírculo es un ángulo recto,
y la otra compartida por dos ilustres geómetras; el Teorema de Pitágoras y la proposición 47 de Euclides.
|
|
al describe el eje vertical del punto de fuga áureo X:
al = 2 + √3/2 |
|
|
|
La Kabala y Las Meninas |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |