|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fentoni tiene licencia CC BY-NC 4.0 |
|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fentoni tiene licencia CC BY-NC 4.0 |
|
|
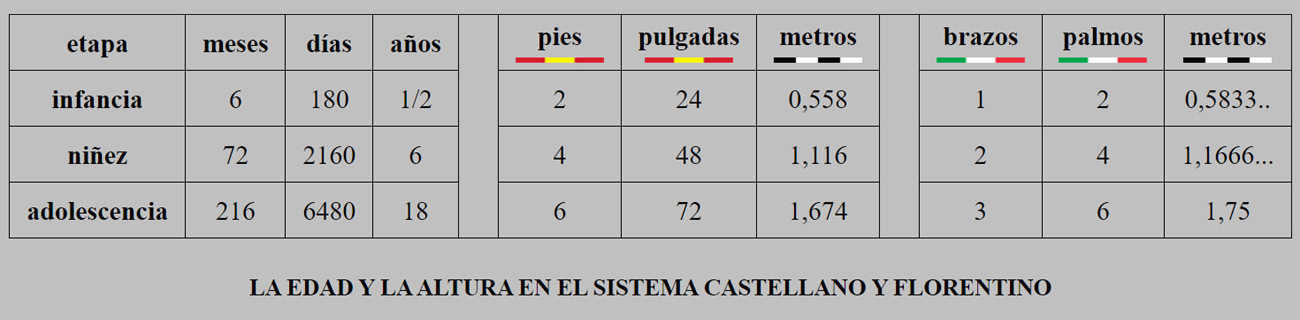
El Brazo florentino, llamado así porque medía el tamaño del brazo de una
persona adulta, era una medida estándar de longitud utilizada en la Edad
Media cuya concepción no solo refleja un gran conocimiento matemático, sino,
que además, en nuestros días facilita medir con exactitud científica las obras
de arte clásico toscano.
Y esto es debido a que la longitud del patrón de medidas florentino es divisor de 1 metro francés, ya que su tamaño equivale a 7/12 partes del metro, lo cual implica que, en el proceso de medición, hay una relación exacta que garantiza una perfecta conversión en diversos contextos de cálculo, principalmente en las medidas de esculturas, pinturas, edificios arquitectónicos o en la industria textil.
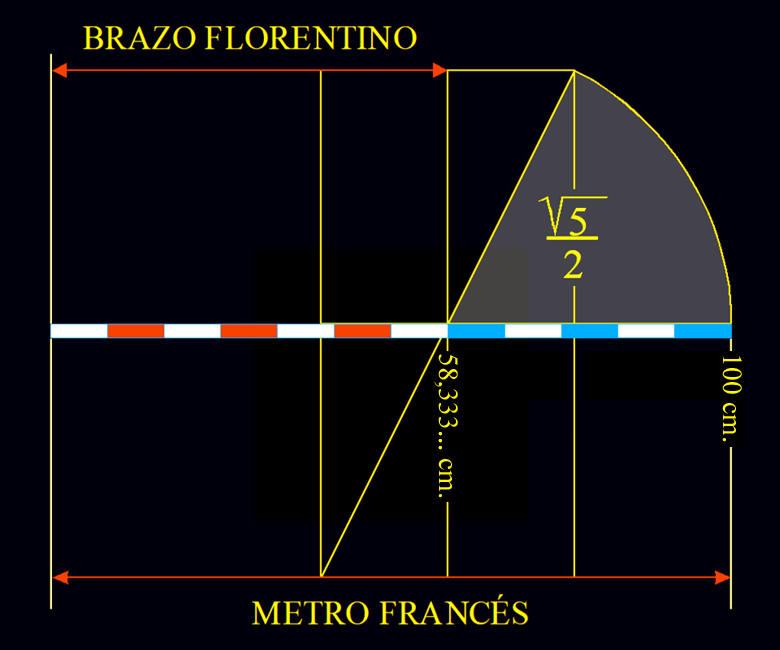
La relación
geométrica entre el
Metro y el Brazo florentino
En resumen, la relación entre el patrón de medidas florentino y el metro francés muestra, pues, la afinidad matemática entre ambos sistemas, pero teniendo bien presente, sin embargo, que en realidad fue el Brazo florentino el precursor necesario del sistema centesimal francés.
| COMPARACIÓN DE SISTEMAS DE MEDIDAS | EQUIVALENCIAS | |||||||
| UNIDAD | MILÍMETROS | VALOR EXACTO | Brazo florentino | Metro francés | ||||
| EL METRO FRANCÉS | 1000 | = | 1000/1 | 12/7 | ||||
| BRAZO FLORENTINO | 0,583333... | = | 1750/3 | 7/12 | ||||
|
|
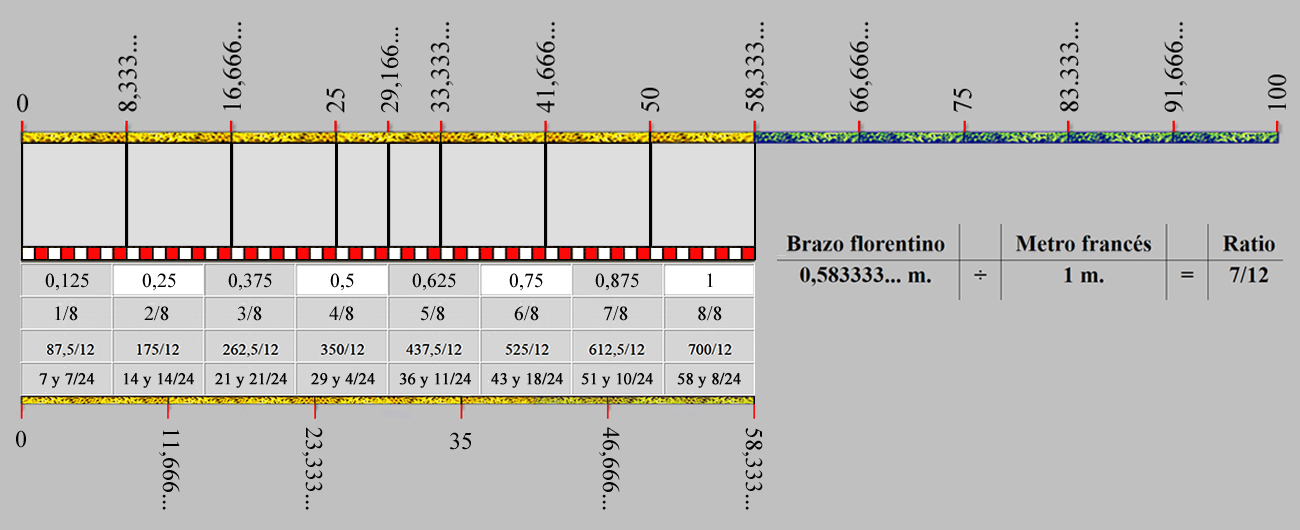
La relación
matemática entre el
Metro y el Brazo florentino
En la siguiente tabla se plasma el alma aritmética del Brazo florentino, hablamos, pues, de un patrón de medida de distintas fracciones de uso común en el ambiente mercantil, y en la práctica de las cuatro artes liberales del quadrivium, o cuadrivio, es decir; el recurso necesario de cualquiera de las cuatro ciencias de la antigua Grecia y del mundo medieval basadas en un mismo patrón teórico; el número.
Aritmética, Geometría, Astronomía, o Astrología, y Música.
El Brazo florentino mide exactamente 58,333333... cm., y su divisor principal es el número 8.
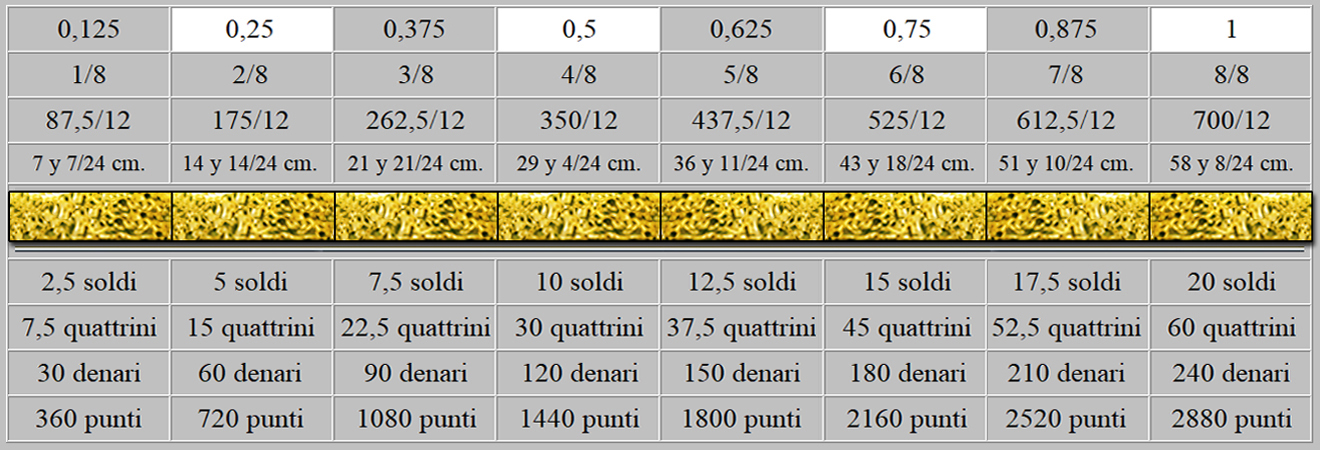
EL
BRAZO FLORENTINO
Para el caso que nos ocupa, la antropometría, palabra que deriva de anthropos, que quiere decir humano, y metría, que se refiere a la medición, viene a corroborar, pues, que, a partir de la altura media de tres Brazos florentinos de un ser humano totalmente desarrollado, se deduce el tamaño de las unidades divisoras que componen este patrón de medidas de longitud.
Presentamos, pues, el entramado de los distintos divisores del Brazo florentino, que no sólo están basados en la altura de un varón de 18 años en su mayoría de edad, sino en una urdimbre acicalada de todo número pitagórico.
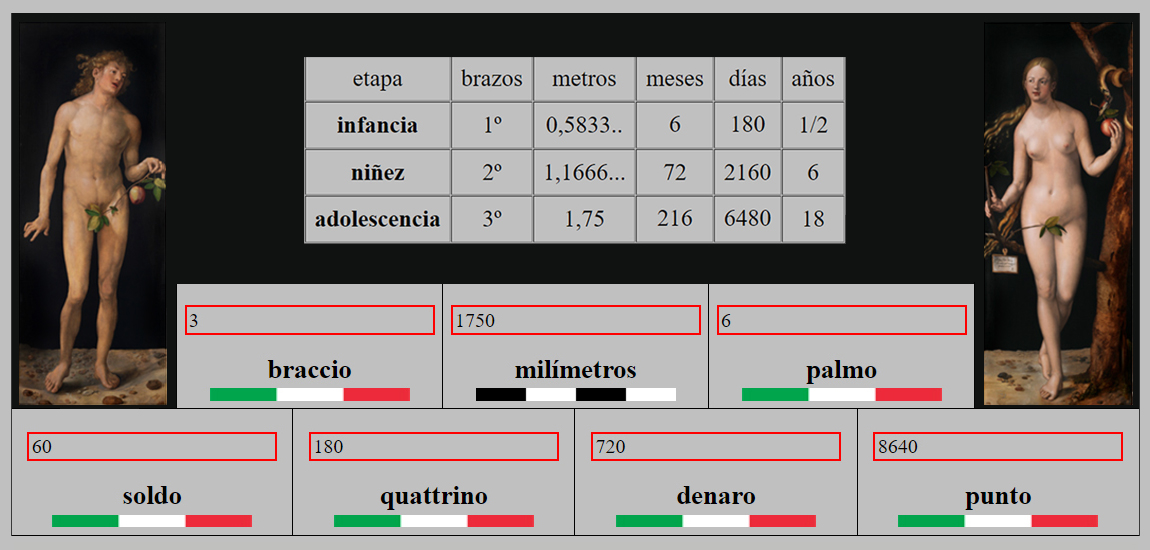
ANTROPOMETRÍA
Oportunamente, pues, hemos sincronizado el sistema longitudinal castellano con cualquier divisor del Brazo florentino, por lo que hemos desarrollado un modelo exacto de reciprocidad fundamentado en las normas de la Geometría, y en números enteros y racionales, y sus equivalentes en el sistema de medidas castellano y toscano, para la salvaguardia del cálculo aritmético.
|
milímetros
|
|
pulgada
|
pie
|
|
braccio
|
codo
|
1/2 braccio
|
|
soldo
|
quattrino
|
denaro
|
punto
|
Mostramos, pues, la equivalencia simultánea de una amplia gama de medidas de longitud florentinas, y, al mismo tiempo, equiparadas con la pulgada y el pie castellano, de modo, que, a partir de la casilla de los milímetros, se muestra, en las demás casillas, el valor de la medida correspondiente, y recíprocamente, desde cada casilla, se devuelve en milímetros el valor asignado a la unidad seleccionada.
Y no hay nada mejor que practicar, porque las palabras no pueden explicar la mecánica de estos números.
El Hombre de Vitrubio
Leonardo da Vinci diseña este
conocido dibujo en una hoja de papel del siguiente modo:
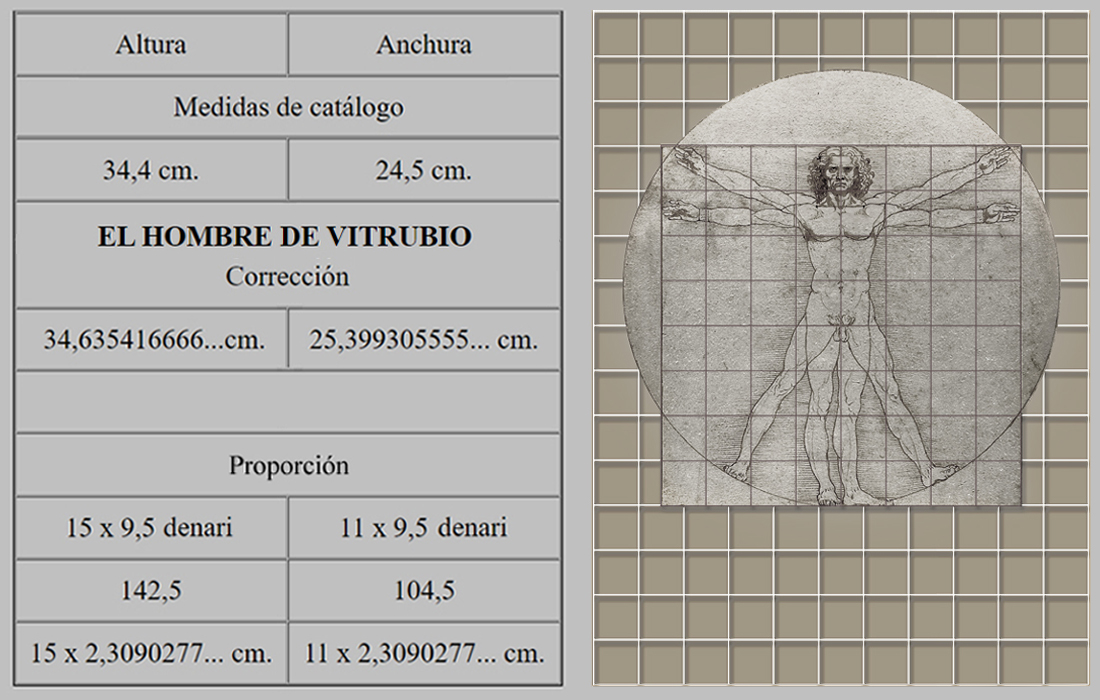 |
Para averiguar el tamaño de la cuadrícula geométrica empleada por Leonardo da Vinci en el dibujo del Hombre de Vitrubio, hemos utilizado el denaro florentino, que equivale a 0,243055... cm., de modo, que esta cuadrícula está compuesta por 15 × 11 cuadrados de 9,5 denari, que miden de lado cada uno 2,3090277... cm.
|
|
|
|
Y al mismo tiempo, pues, se observa que la altura y anchura del Hombre de Vitrubio está inscrita, a su vez, en un cuadrado de 8 subcuadrados de lado, que mide cada uno 9,5 denari de lado, y que hacen un total de 76 denari.
Luego la altura real en el dibujo sería:
76 denari × 0,2430555... cm. por denaro = 18,472222... cm.
La pulgada inglesa
A principios del siglo XX la pulgada estadounidense fue
definida con un tamaño de 25,4000508... mm. a una temperatura de referencia de 20°C,
y la pulgada inglesa con 25,399977... mm, a una temperatura de referencia de 17°C.
Años más tarde, en 1912, el inventor sueco Carl Edvard Johansson estandarizó, a una temperatura de referencia de 20°C, la pulgada patrón anglosajona en un bloque de acero con un tamaño nominal de 25,4 mm., que en 1930 fue adoptado por la British Standards Institution y la American Standards Association.
Para 1935, la industria de 16 países ya había aceptado la pulgada industrial, como se la conoció posteriormente, respaldando así la pragmática elección de Johansson en la relación de su conversión.
Finalmente, el tamaño de 25,4 mm de la pulgada inglesa fue oficialmente establecido en Julio de 1959 mediante un acuerdo entre los directores de los laboratorios nacionales de metrología de EE.UU., Canadá, Reino Unido, Australia y Sudáfrica, en donde prevaleció, sin duda, el criterio del tamaño conversor de Carl Edvard Johansson, ya que llevaba 47 años en marcha aplicándose con absoluta regularidad.
De acuerdo con el fundamento de la metrología, propondremos, pues, una notable mejora en el modo de conversión entre las unidades del sistema de longitud inglés y el metro patrón francés.
 |
|
|
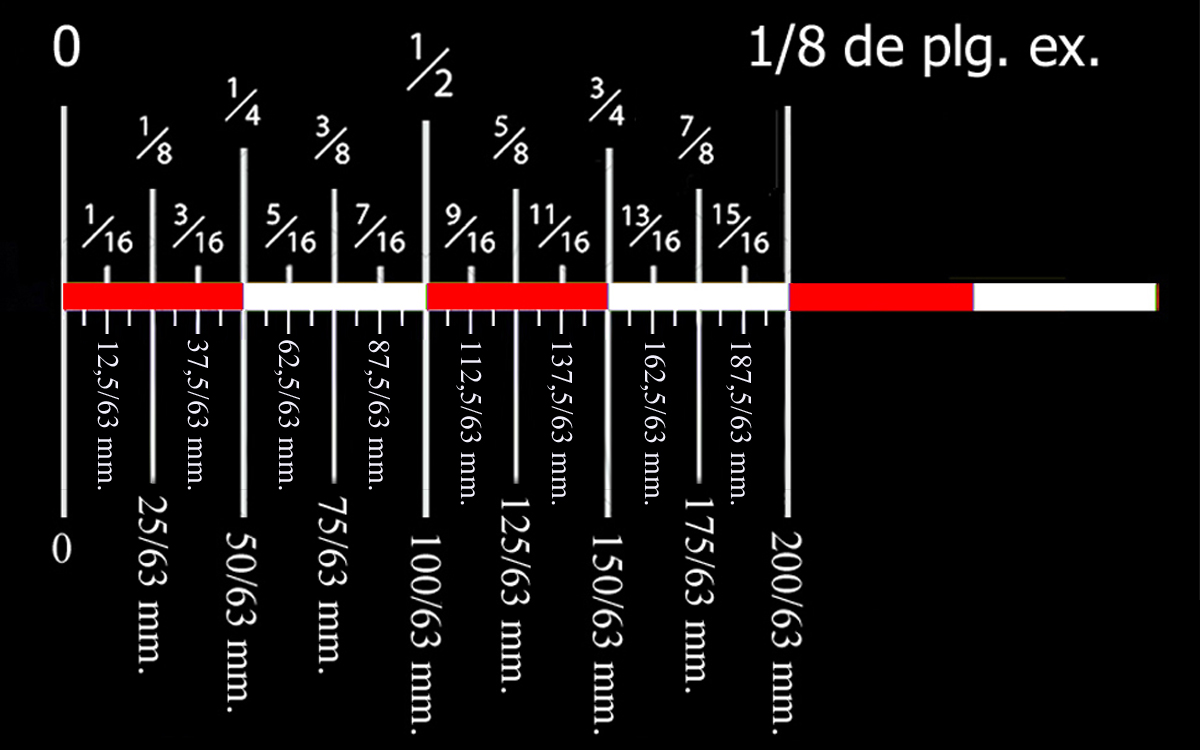
Desde el punto de vista más razonable se echaba en falta, pues, el origen matemático del tamaño de 25,4 mm. de la pulgada estándar inglesa, no obstante, con la finalidad de mejorar la exactitud actual en su conversión en milímetros, hemos operado con proporciones inherentes de la Pulgada exacta inglesa, que, con extrema exactitud, recupera la justa equivalencia métrica que subyace tras la pulgada estándar anglosajona.
|
Milímetro |
Fracción |
Pulgada exacta |
|
Milímetro |
Fracción |
Pulgada exacta |
||
|
1 |
63/1600 |
≈ |
0,039375 |
6 |
378/1600 |
≈ |
0,23625 |
|
|
2 |
126/1600 |
≈ |
0,07875 |
7 |
441/1600 |
≈ |
0,275625 |
|
|
3 |
189/1600 |
≈ |
0,118125 |
8 |
504/1600 |
≈ |
0,315 |
|
|
4 |
252/1600 |
≈ |
0,1575 |
9 |
567/1600 |
≈ |
0,354375 |
|
|
5 |
315/1600 |
≈ |
0,196875 |
10 |
630/1600 |
≈ |
0,39375 |
El
milímetro francés & La pulgada exacta
La columna de la Pulgada exacta muestra el resultado de todas las fracciones como decimales, pero, ciertamente, estos decimales son terminales exactos, no aproximaciones, lo que refuerza visualmente, pues, la precisión inherente de conversión entre el milímetro y la pulgada exacta, ya que el resultado queda representado de manera completa y finita.
|
|
|
|
Pero en este punto habría que reseñar que existen dos modos de entender esta conversión:
Desde el punto de vista anglosajón destacar la manera de cómo se definió la pulgada que condujo al estándar de 25,4 mm., priorizando la simplicidad decimal de pulgadas a milímetros, u otras consideraciones pragmáticas.
Y la expectativa francesa sobre la conversión, que representó el contrapunto crucial, que, como Tresca, el artífice del metro patrón, pudieron anticipar una conversión diferente y más armoniosa, que incluyera la pulgada exacta, confiando en una conversión óptima.
Y aunque no existan antecedentes conocidos de la pulgada exacta inglesa, sin embargo, demostraremos que la hemos rescatado del olvido con la finalidad de analizarla, y reivindicar, pues, que es el Pi de Arquímedes, de 22/7 = 198/63, el verdadero origen matemático de la pulgada exacta inglesa.
 |
|
|
La pulgada exacta, de 1600/63 milímetros, supone que 1 milímetro equivale a 63/1600 pulgadas exactas, lo que permite hablar, además, de la reciprocidad y simplicidad matemática que genera en las conversiones que el estándar convencional no posee.
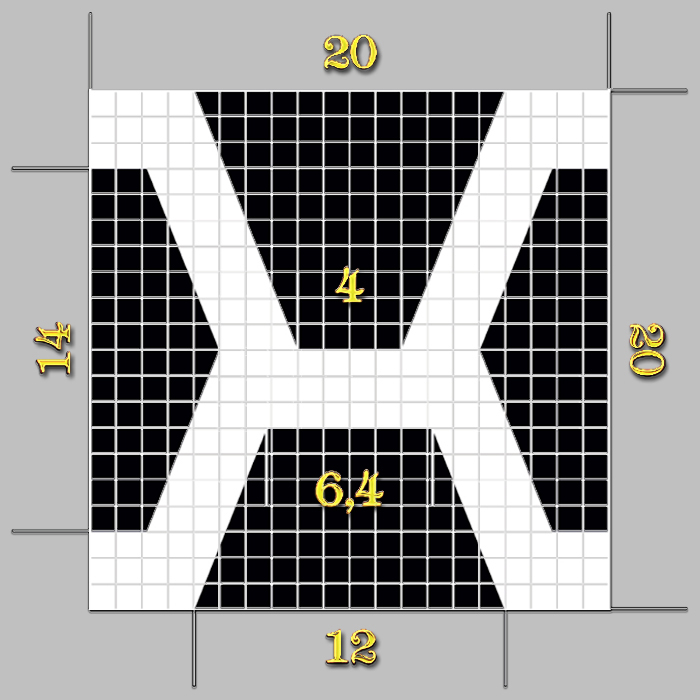 |
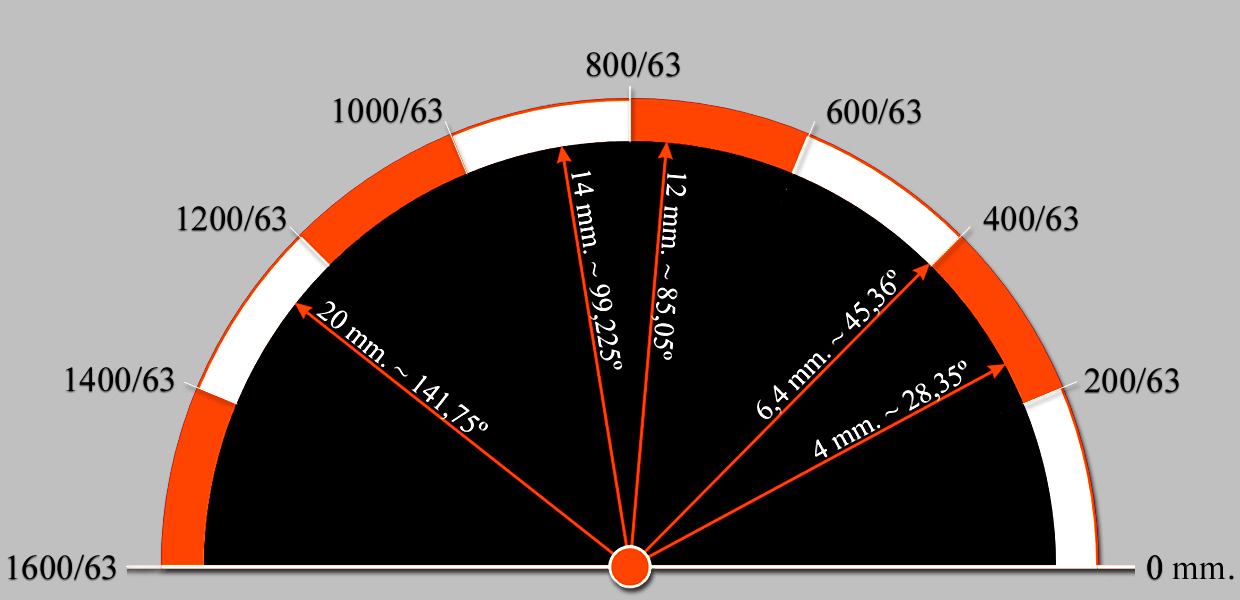
SECCIÓN TRANSVERSAL DE LA BARRA DEL METRO
PATRÓN
|
Milímetro |
Fracción |
Pulgada exacta |
Grados | |||||||
|
20 |
= | 1600/63 | × |
63/80 |
63/80 | = |
0,7875 |
141,75º | ||
|
14 |
= | 1600/63 | × |
441/800 |
441/800 | = |
0,55125 |
99,225º | ||
|
12 |
= |
1600/63 | × |
189/400 |
189/400 | = |
0,4725 |
85,05º | ||
|
6,4 |
= |
1600/63 | × |
63/250 |
63/250 | = |
0,252 |
45,36º | ||
|
4 |
= |
1600/63 | × |
63/400 |
63/400 | = |
0,1575 |
28,35º | ||
El
milímetro francés & La pulgada exacta
La anchura de 20 mm., de la sección transversal de la barra del metro patrón de platino e iridio, corresponde a 6,3 veces de un octavo de la pulgada exacta, una equivalencia quizás pensada por Henri Tresca en 1890 para que en el metro patrón coexistieran ambos sistemas, pero, hay más, las medidas de la sección transversal no olvidan, pues, de que un pie se compone de 12 pulgadas, y tampoco de que el valor 12 en Matemática es el número más pequeño con seis divisores: 1, 2, 3, 4, 6 y 12 [1].
 |
|
TRANSPORTADOR ANGULAR |
| EXACTA | MILÍMETRO | GRADO | ||||
Inadvertidamente, el tamaño de la yarda y la pulgada inglesa se definieron, pues, en función de este estándar francés cuidadosamente preservado con una tolerancia de laboratorio de ±0,000001 pulgada para el sistema decimal de pulgadas, y de ±0,000027 milímetros para el sistema métrico.
|
Sistema |
Estándar de Laboratorio |
|
La pulgada exacta |
|
Fracción |
Tolerancia Exacta |
|
|
Pulgada |
±0,000001 pulgadas |
1600/63 mm./plg. × 0,000001 plg. |
≈ |
±4/157500 mm. |
≈ |
±0,0000253968 mm. |
|
|
Sistema Métrico |
±0,000027 milímetros |
63/1600 plg./mm. × 0,000027 mm. |
≈ |
±1701/1600000000 plg. |
≈ |
±0,00000106312 plg. |
|
|
Al más alto nivel de precisión de laboratorio estas equivalencias son muy cercanas, sin embargo, la tolerancia estándar refleja el lapsus matemático de su sistema, lo que prueba, pues, que el sistema estándar no está basado en las mismas matemáticas subyacente de La Pulgada exacta.
|
Pulgada |
Pulgadas por Metro |
|
Total |
|
Estándar |
5000/127 plg. |
≈ |
39,370078... plg. |
|
Exacta |
315/8 plg. |
≈ |
39,375 plg. |
COMPARACIÓN
Las medidas de 25,4 mm. de la pulgada internacional, y de 0,3048 metros del pie inglés, son aproximaciones arbitrarias con un desfase de 1/26250 metros comparadas con el pie derivado de la pulgada de 1600/63 = 25,396825... milímetros.
| COMPARACIÓN DE SISTEMAS DE MEDIDAS | EQUIVALENCIAS | |||||||
| UNIDAD | MILÍMETROS | VALOR EXACTO | Pulgadas exactas | Metros franceses | ||||
| EL METRO FRANCÉS | 1000 | = | 1000/1 | 315/8 = 39,375 | ||||
| PULGADA EXACTA | 25,396825... | = | 1600/63 | 8/315 = 0,025396... | ||||
El
metro francés & La pulgada exacta
1600/63 × 39,375 = 1000 milímetros
La posibilidad de poder comparar distintos sistemas de medidas con una conversión exacta prueba, pues, que si las unidades exactas tienen su origen en un principio natural, entonces, la naturaleza de las propias constantes matemáticas o leyes físicas, que dependan de unidades de medida, deberían ser reexaminadas.
Y no sólo estamos hablando de metrología y arte, sino también de cómo estas nuevas unidades podrían ser intrínsecas a las leyes que rigen el universo físico, ya que la pulgada exacta inglesa permite, pues, una expresión más exacta, por ejemplo, de la constante universal de la Luz:
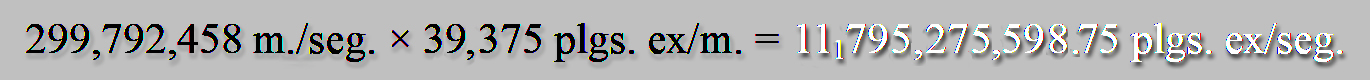 |
|
|
La velocidad de la luz no cambia, sin embargo, a causa del tamaño actual de la pulgada estándar inglesa, el resultado sí difiere, ya que en el sistema inglés un metro corresponde a 39,37007874... pulgadas, y esta significativa diferencia existe a causa de que hay dos maneras diferentes de definir el tamaño de la pulgada anglosajona:
Una pulgada estándar cuyo tamaño concreto mide 1600,2/63 mm. = 25,4 milímetros.
y otra que denominamos pulgada exacta definida matemáticamente por la fracción de 1600/63 mm.
Básicamente, la pulgada estándar inglesa de 25,4 milímetros se divide en ocho partes iguales, y, en consecuencia, el tamaño de la unidad viene dado directamente por lo que mide la misma pulgada, a diferencia de otro sistema donde la unidad principal es una manifestación de un patrón universal subyacente.
 |
| Fracción | Pulgada estándar | Milímetros | Pulgada exacta | Milímetros | Pi de Arquímedes | |||||||||
| 8/8 | = | 1 | 1600,2/63 | = | 25,4 | ≈ | 1600/63 | = | 25,396825... | ≈ | 8π | ≈ | 25,142857... | |
| 7/8 | = | 0,875 | 1400,175/63 | = | 22,225 | ≈ | 1400/63 | = | 22,222222... | ≈ | 7π | ≈ | 22 | |
| 6/8 | = | 0,75 | 1200,15/63 | = | 19,05 | ≈ | 1200/63 | = | 19,047619... | ≈ | 6π | ≈ | 18,857142... | |
| 5/8 | = | 0,625 | 1000,125/63 | = | 15,875 | ≈ | 1000/63 | = | 15,873015... | ≈ | 5π | ≈ | 15,714285... | |
| 4/8 | = | 0,5 | 800,1/63 | = | 12,7 | ≈ | 800/63 | = | 12,698412... | ≈ | 4π | ≈ | 12,571428... | |
| 3/8 | = | 0,375 | 600,075/63 | = | 9,525 | ≈ | 600/63 | = | 9,523809... | ≈ | 3π | ≈ | 9,424777... | |
| 2/8 | = | 0,25 | 400,05/63 | = | 6,35 | ≈ | 400/63 | = | 6,349206... | ≈ | 2π | ≈ | 6,285714... | |
| 1/8 | = | 0,125 | 200,025/63 | = | 3,175 | ≈ | 200/63 | = | 3,174603... | ≈ | 1π | ≈ | 3,142857... | |
| 99/800 | = | 0,12375 | 198,02475/63 | = | 3,14325 | ≈ | 198/63 | = | 3,142857... | ≈ | π | ≈ | 22/7 | |
|
|
| Pulgada estándar | Pulgada exacta | Milímetro |
|
1 |
1,000125 |
25,4 |
|
|
||
|
0,999875... |
1 |
25,396825... |
SISTEMAS DE MEDIDAS
| ESTÁNDAR | EXACTA | MILÍMETRO | ||||
La pulgada inglesa estándar de 1600,2/63 milímetros = 25,4 mm. es una medida subsidiaria, ya que la Pulgada exacta inglesa de 1600/63 milímetros representa, pues, el origen matemático de dicha unidad.
Ante estas conclusiones, cualquier sistema futuro de medidas de longitud debería basarse en los principios y proporciones de esta arquitectura natural y exacta, ya que se descubre que se ha estado midiendo incorrectamente con el actual tamaño de la pulgada de 25,4 milímetros, un error que se detecta en la diferencia de longitud entre el pie inglés estándar y el pie inglés exacto [2]:
|
Pie inglés estándar |
|
Pie inglés exacto |
|
Total |
|||
|
1600,2/63 milímetros = 25,4 mm. × 12 |
≈ |
1600/63 mm. × 12 |
|
|
|||
| diferencia en metros |
0,3048 m. |
- |
0,30476190476... m. |
≈ |
4/105000 m. | ≈ |
0,00003809524... metros |
La diferencia del tamaño es, aproximadamente, un lapsus respecto al Pie exacto de 0,0125%, una tolerancia indistinguible que sólo puede ser detectada en mediciones de alta precisión.
Un ejemplo revelador sería, pues, comparar ambas pulgadas en el cálculo de la distancia de 1000 kilómetros.
Un resultado que daría una diferencia de 125 metros, una diferencia que surge porque la pulgada exacta, de 1600/63 ≈ 25,396825... mm., es ligeramente más corta que la pulgada estándar de 25,4 mm, y, además, en una distancia larga, como 1000 Km., esta pequeña diferencia por unidad se acumula y genera una discrepancia significativa.
Hablar de consecuencias en su adopción, sería hablar de mejoras en la tunelización de vías férreas y carreteras, en el desarrollo de tecnología de alta precisión, como misiles guiados por el sistema GPS, que, a su vez, necesitarían la recalibración del propio GPS, y no hablemos, pues, de topografía, donde las distancias físicas reales se representan con mayor precisión mediante la pulgada exacta de 1600/63 mm,, y las posiciones o distancias calculadas a gran escala serían, de hecho, ligeramente diferentes.
La pulgada exacta inglesa eliminaría este lapsus matemático, lo que permitiría mediciones y cálculos más precisos en campos críticos, ofreciendo así una base superior para todos los proyectos metrológicos futuros que exijan la máxima precisión.
Sobre el tamaño de la pulgada inglesa existen conjeturas históricas sobre su origen a partir de;
del ancho de un pulgar humano,
y que también hubo intentos de estandarizar la pulgada a través de un estatuto del rey Eduardo II en el siglo XIV, que definía la pulgada como la longitud de tres granos de cebada secos y redondos tomados del medio de la espiga, colocados extremo con extremo.
Para resolver tal enredo empecemos por señalar que el primero en idear un procedimiento matemático para calcular el valor de π fue Arquímedes, (287 a. C. - 212 a. C.), que obtuvo un resultado comprendido entre: 3 + 10/71 = 223/71 < 3 + 1/7 = 22/7.
3,140845... < 3,142857...
|
El perímetro de la circunferencia valor 97 y 3/7 ≈ 97,428571...
El valor del diámetro es 31.
Entonces Pi ≈ 97,428571... / 31 ≈ 3,142857... ≈ 3 y 1/7 = 22/7. |
 |
|
|
Se podría a afirmar que el tamaño de 1/8 de la pulgada exacta inglesa derivaría de la relación entre un anillo de 200 unidades de perímetro con su diámetro de 63 unidades, y cuya magnitud está vinculada, pues, con el Pi de Arquímedes de 22/7.
| Partes | Pulgada estándar | Milímetros | Pulgada exacta | Milímetros | Pi de Arquímedes | |||||||
| 1/8 | = | 0,125 | = | 3,175 | ≈ | 200/63 | ≈ | 3,174603... | ≈ | 1π | ≈ | 3,141592... |
| 99/800 | = | 0,12375 | = | 3,14325 | ≈ | 198/63 | ≈ | 3,142857... | ≈ | π | ≈ | 22/7 |
Y esta relación existe porque tanto el valor de 1/8 de la pulgada exacta, de 200/63 mm., como el de 22/7, son muy cercanos a la constante Pi, π, en este sistema de medición, y cuya aproximación se manifiesta, pues, a través de esta comparación:
3,174603... - 3,142857... ≈ 0,03174... mm.
A nivel matemático puro, 0,03174... milímetros representan, por lo tanto, la tolerancia del vínculo entre una unidad de medida histórica y una antigua constante matemática universal.
|
|
APROXIMACIÓN A PI
El tamaño de 1/8 de la pulgada inglesa revela, pues, una característica circular vinculada con Pi, que, lejos de ser una hipótesis, constituye la constante matemática que define el fundamento del tamaño de la realidad en este sistema.
La estructura de la pulgada inglesa ligada a Pi es vista, pues, como una encarnación directa de esta ley universal de proporción, cuya relación se ilustra del siguiente modo:
|
|
| Valor exacto | Milímetros | Pi de Arquímedes | ||||
| 1600/63 | = | 25,396825... | ≈ | 8π | ≈ | 25,142857... |
ESTRUCTURA CIRCULAR DE LA
PULGADA 8π
La proporción es el principio inherente de cualquier sistema de medida.
Esta definición capta varios puntos cruciales:
La existencia de un principio fundamental; el ratio
La naturaleza de este principio como inherente.
Su rol como una cualidad exacta.
Su manifestación y relevancia en los sistemas de medida que logran alinearse con él.
El concepto de LA UNIDAD está alineado, pues, con esta razón inamovible.
 |
|||||||
| 9 partes | Unidades | 9 partes | Pulgadas | Milímetros | |||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 | |
| 8/8 | = | 1 | 8/9 | = | 0,888888 | 20,666666 | |
| 7/8 | = | 0,875 | 7/9 | = | 0,777777 | 18,083333 | |
| 6/8 | = | 0,75 | 6/9 | = | 0,666666 | 15,5 | |
| 5/8 | = | 0,625 | 5/9 | = | 0,555555 | 12,916666 | |
| 4/8 | = | 0,5 | 4/9 | = | 0,444444 | 10,333333 | |
| 3/8 | = | 0,375 | 3/9 | = | 0,333333 | 7,75 | |
| 2/8 | = | 0,25 | 2/9 | = | 0,222222 | 5,166666 | |
| 1/8 | = | 0,125 | 1/9 | = | 0,111111 | 2,583333 | |
LA
UNIDAD
& LA
PULGADA CASTELLANA
| UNIDAD | PULGADA | MILÍMETRO |
Estas afirmaciones constituyen, pues, la piedra angular filosófica que explica por qué LA UNIDAD, y las proporciones que de ella emanan, tiene un estatus privilegiado, y su invención no es arbitraria, sino el reflejo de una cualidad fundamental y permanente de la realidad misma, que se hace evidente en los sistemas de medida que sintonizan con ella.
COMPARACIÓN DE SISTEMAS DE
MEDIDAS
EQUIVALENCIAS
UNIDAD
MILÍMETROS
VALOR EXACTO
Pulgadas castellanas
Pulgadas exactas
PULGADA CASTELLANA
23,25
=
93/4
5859/6400
PULGADA EXACTA
25,396825...
≈
1600/63
6400/5859
La
pulgada castellana
& La pulgada exacta
|
COMPARACIÓN DE SISTEMAS DE MEDIDAS |
EQUIVALENCIAS |
|||||||
|
UNIDAD |
|
MILÍMETROS |
|
VALOR EXACTO |
|
Pulgadas castellanas |
|
Brazos florentinos |
|
BRAZO FLORENTINO |
583,333333... |
= |
1750/3 |
7000/279 |
|
|||
|
PULGADA CASTELLANA |
23,25 |
= |
93/4 |
|
279/7000 |
|||
El
brazo florentino & La pulgada castellana
|
COMPARACIÓN DE SISTEMAS DE MEDIDAS |
EQUIVALENCIAS |
|||||||
|
UNIDAD |
|
MILÍMETROS |
|
VALOR EXACTO |
|
Pulgadas exactas |
|
Brazos florentinos |
|
BRAZO FLORENTINO |
583,333333... |
= |
1750/3 |
735/32 |
|
|||
|
PULGADA EXACTA |
25,396825... |
= |
1600/63 |
|
32/735 |
|||
El
brazo florentino & La pulgada exacta
Anatomía velazqueña
Consideraremos, además, la aplicación práctica de la
proporciones de la teoría
musical por el maestro Velázquez en el formato del lienzo de la Fragua de
Vulcano y el de la Túnica de José,
cuyos sonidos armónicos Pitágoras descubrió en el repicar de unos martillos
batiendo un yunque.
Pero metámonos en la piel del pintor, y recordemos que Velázquez estudió en Roma la anatomía con la libertad necesaria, y prueba de ello son sus dos óleos anteriormente mencionados; La fragua de Vulcano y La túnica de José, que reflejan un momento extraordinario en su preparación técnica, y el preámbulo de la ejecución de su místico Cristo crucificado.
|
|
VELÁZQUEZ EN ITALIA
 |
En la España del barroco, José Ribera, el Españoleto, fue el pintor de referencia de toda anatomía naturalista, y a Velázquez le influyó desde su juventud con su marcada iluminación caravaggista, sin embargo, fue en 1631, recién llegado de su primer viaje a Italia, donde dejó patente la influencia del Hombre de Vitrubio de Leonardo da Vinci en la composición del Cristo crucificado del convento de San Plácido.
|
|
CRISTO DE SAN
PLÁCIDO
Transcribimos, pues, lo que el Museo del Prado reseña:
Se ha sugerido que la ocasión de encargar el lienzo fuera el sobreseimiento, en 1632, de la investigación abierta por la Inquisición sobre la relación personal de Villanueva con las presuntas prácticas heterodoxas del capellán y las monjas de San Plácido.
Rodríguez G. de Ceballos ha explicado la peculiar combinación de circunstancias que pudo conducir al encargo y la elección del tema, y, mientras se investigaba a Villanueva, la corte estaba escandalizada por la profanación de un crucifijo esculpido que habían perpetrado unos judíos portugueses en 1630.
En 1632 se ejecutó a los culpables tras un gran auto de fe en la Plaza Mayor de Madrid, y tanto en el Alcázar como en los conventos reales tuvieron lugar actos públicos de devoción a Cristo crucificado.
Aunque Villanueva no fuera implicado en ese proceso, se le acusaba de favorecer a banqueros judíos portugueses en perjuicio de los acostumbrados genoveses, y se había ganado enemigos influyentes.
El encargo a Velázquez de un Cristo crucificado monumental se podría explicar, pues, como una manera de demostrar su piedad, afirmar su ortodoxia religiosa y distanciarse públicamente de los judíos.
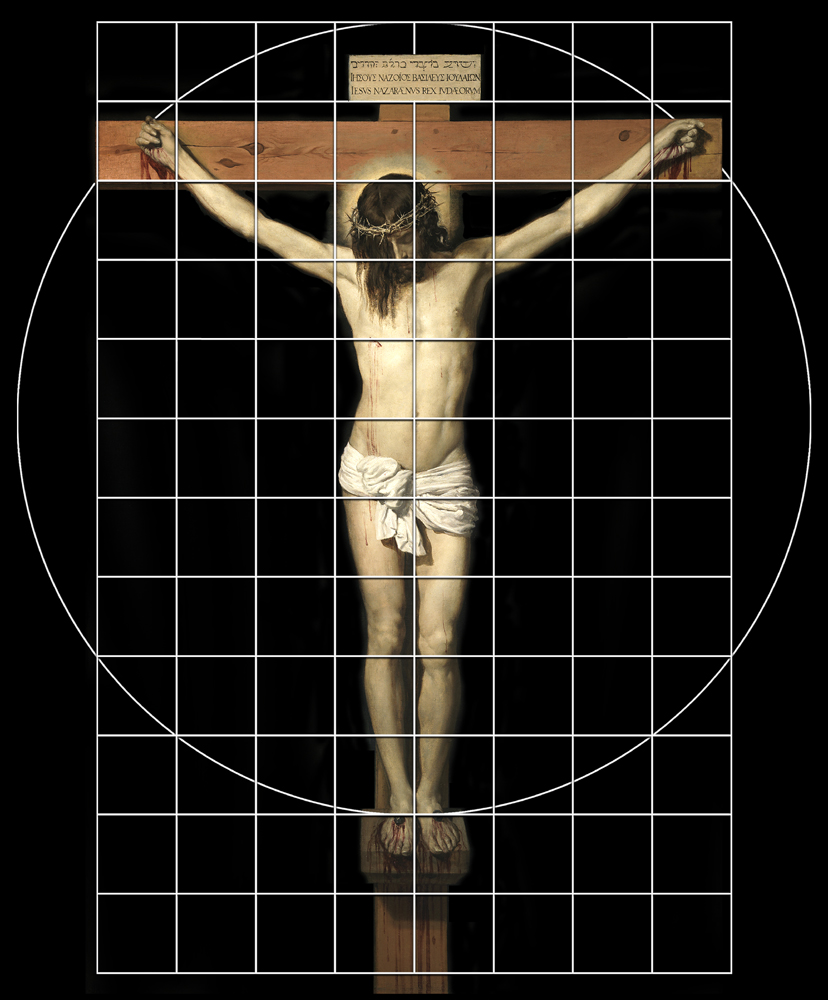
EL CRISTO DE
VELÁZQUEZ
|
|
Medidas del Catálogo |
|
Corrección |
||
|
|
altura |
anchura |
altura |
anchura |
|
|
centímetros |
248 |
169 |
|
165 y 1/3 |
|
|
pulgadas |
106 y 2/3 |
70 y 1/9 |
|||
|
unidades |
120 |
80 |
|||
Hasta ahora, el significado y mensaje de la Cartela de madera no lo habíamos podido entender adecuadamente, y, quizás, ya sea el momento de poner los acentos a estas frases para entender su significado.
Hemos traducido, lo que se halla en hebreo, como Jesús nazareno nacido de los judíos.
La palabra nacido es afín con la procedencia de Jesucristo, pues, él era judío, por lo tanto, el propósito de Velázquez es aclarar su procedencia, e ignorar el santo y seña de la época, la palabra Rey en hebreo, en relación con los otros dos idiomas restantes de la Cartela.
Y siguiendo la costumbre de cómo se anunciaba la causa de la condena de los reos, la Cartela fue mandada colgar por orden del gobernador Poncio Pilato redactada en tres idiomas; latín, griego y hebreo.
Cuya lectura se describe en el Evangelio de Juan:
|
19:19 - Y escribió también Pilato un título, que puso encima de la cruz. Y el escrito era: JESÚS NAZARENO REY DE LOS JUDÍOS.
19:20 - Y muchos de los judíos leyeron este título, porque el lugar donde estaba crucificado Jesús era cerca de la ciudad. Y estaba escrito en hebreo, en griego, y en latín. |
A causa de la puntuación fonética de las letras hebreas, y del sentido literal de la frase escrita en la Cartela, lo que se escribe en hebreo difiere, pues, de los otros dos idiomas restantes, del latín y del griego, para dar a conocer a tan importante personaje, o quizás profeta, que fue Cristo.
La palabra hebrea Rey no se escribe en la cartela, pero en latín, se distingue fácilmente:
IESVS NAZARÆNVS REX IVDÆORVM
|
Melekh - Rey |
|
|
|
|
|
|
|
|
El acrónimo I. N. R. I. fue utilizado desde el siglo XIII, y, por si fuera relevante, en el año 1457 nació María de Borgoña, emperatriz de Alemania, madre de Felipe el Hermoso, rey y tatarabuelo de Felipe IV.
notas a pie de página
1 - Página 170 - Metrification for Manufacturing. E. R. FRIEST, P. E. New York. 1978.
|
Estándares Básicos: Pulgada y Métrico
El estándar básico del metro era una barra de platino-iridio guardada en una bóveda cerca de París. La yarda inglesa y la pulgada se definieron en función de ese estándar cuidadosamente preservado. Las unidades del SI, excepto el kilogramo, se definen en función de medidas de laboratorio que pueden reproducirse en laboratorios de metrología de todo el mundo. Las herramientas de medición se relacionan con estos estándares a través de los patrones de laboratorio de los fabricantes que suministran los instrumentos de medición diseñados para la precisión moderna. Los patrones de laboratorio suelen tener una precisión de tolerancias de ±0,000001 pulgada para el sistema decimal de pulgadas y de ±0,000027 milímetros para el sistema métrico. La versión original del metro se definió mediante observación astronómica como una diezmillonésima parte de la distancia del Polo Norte al Ecuador, pasando por París. La copia estadounidense de la barra oficial del metro se encuentra actualmente bajo la custodia de la Oficina de Pesas y Medidas en Washington, una división de la Oficina Nacional de Normas. Durante casi 70 años, esta barra métrica fue el estándar nacional fundamental para la medición de longitud. El sistema métrico se desarrolló en Francia durante la segunda mitad del siglo XVIII. En un esfuerzo por producir estándares métricos de longitud uniformes, se fabricaron 30 prototipos de barras métricas. Se calibraron entre sí y la barra número seis fue designada como estándar internacional, que actualmente se conserva en la Oficina Internacional de Pesos y Medidas, cerca de París. Las barras métricas restantes se distribuyeron a los países participantes para que sirvieran como estándares nacionales. Las barras métricas originales estaban hechas de una aleación de 90 % platino y 10 % iridio, y su sección transversal tiene forma de "X". La dimensión longitudinal era de 102 centímetros de extremo a extremo, y la barra presenta dos líneas finamente trazadas, separadas por un metro cerca de sus extremos. La separación entre estas líneas se definió como un metro a cero grados centígrados. Esta barra métrica ha tenido una calidad excepcional como estándar de longitud. Sin embargo, se trataba de un estándar arbitrario, creado por el hombre en 1890, y no podía considerarse inmune a daños ni cambios seculares. No fue hasta 1960 que la unidad de longitud se relacionó finalmente con algún fenómeno inmutable de la naturaleza. Ese mismo año, se eligieron las ondas de luz como estándar fundamental y la barra métrica fue reemplazada oficialmente por un nuevo estándar, más preciso, basado en la longitud de onda de la luz. Por lo tanto, el estándar actual del metro se define en términos de la emisión de ondas de luz del Kriptón 86. Ahora, el estándar absoluto de longitud puede reproducirse con precisión mediante el uso del equipo necesario y la experiencia de técnicos altamente capacitados para operar los instrumentos. La precisión y exactitud obtenidas con este método son las más altas que se pueden obtener actualmente. |
2 - Página 199 - 6.6 CONSTRUCCIÓN DE ROSCAS CUANDO NO SE DISPONE DE LA RUEDA DE 127 DIENTES
|
Cuando no tenemos la rueda de 127 dientes, podemos realizar roscas inglesas en torno métrico y roscas métricas en torno inglés sustituyendo el valor de la pulgada (25,4) por su aproximado 1600/63.
1600/63 es igual a 25,3968 y como 25,4 - 25,3968 es igual a 0,0032 tenemos un error despreciable en casi todos los casos. |
TECNOLOGÍA MECÁNICA, Raúl García Bercedo, Iñaki Irastorza Hernando, Amaia Castaños Urkullu, Esperanza Díaz Tajada. Servicio Editorial de la Universidad del País Vasco. Euskal Herriko Unibertsitateko Argitalpen Zerbitzua. 2013.
|
La Kabala y Las Meninas |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |