|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fantoni tiene licencia CC BY-NC 4.0 |
|
|
Velázquez - La Kabala y Las Meninas © 1991 de Ignacio Benjumea Fantoni tiene licencia CC BY-NC 4.0 |
|
|
Las Meninas de Diego Velázquez
Más allá del valor estético, lo esencial en el
estudio de
una obra de arte es interpretar el mensaje que se emite, y,
conjuntamente, como es el caso del óleo de Las Meninas, considerar
aparte la intención de su autor Diego Velázquez, pese a que se
halle en el proceso de conocerse, y espere solícita en la antesala de la opinión de eminentes figuras de las
ciencias, letras y artes, que descartó la sospecha del apego del maestro
español a una de las herencias más prohibidas de la península Ibérica:
La ley de Boca, también llamada La Kabala.
El Árbol de la Vida, como punto de partida, está integrado en el espacio aéreo de esta pintura, y, su Geometría, no sólo ofrece la reflexión más profunda del genio indiscutible de la pintura española, sino que descubre, a todos los estudiosos de la obra de Diego de Silva Velázquez, un legado consumado que el tiempo no ha podido borrar.
Hablamos, pues, de una subversión total del balcón del poder, donde la Monarquía Hispánica se presentaba ante el mundo como el martillo de la Contrarreforma y el brazo armado del Catolicismo, sin embargo este análisis sugiere que, en la intimidad de sus aposentos, buscaba la salvación en la Kabala, un conocimiento perseguido por su propia Inquisición.
Esta investigación profundiza en características desconocidas de Las Meninas, y marca la diferencia ante las explicaciones tradicionales, lo que obliga a reconsiderar, bajo la luz de la España del siglo XVII, el inexplorado vínculo de esta escena pictórica con la superstición y la doble moral en el Real Alcázar de Madrid.
En otras palabras, en el escenario de Las Meninas se perfila una inusual situación hereditaria con la intención de influir, mediante antiguas prácticas ceremoniales, en el destino político de la dinastía de los Austrias.
|
|
|
|
La protección mágica
La puesta en escena de Las Meninas se
desarrolla en el Cuarto del Príncipe Baltasar Carlos, quien
falleció en Zaragoza el 9 de Octubre de 1646 antes de cumplir diecisiete años,
un triste
desenlace que alteró profundamente el futuro de la Corona española
[1].
Diez años después, en esta misma sala del Alcázar, Velázquez, no solo retrataba a la Infanta Margarita como posible heredera, sino que situó al aposentador José Nieto en la escalera de Rubinejo custodiando el acceso a la sabiduría de las veintidós letras del alefato hebreo, que, a modo de talismán protector contra peligros y enfermedades, funcionan con el propósito de exorcizar en la pintura el fracaso dinástico marcado por la muerte del príncipe heredero.
Los 22 cuarterones labrados en esta Puerta castellana resumen, de un vistazo, la declaración ideológica del antiguo lenguaje sagrado, donde, además, José Nieto es el único que puede observar, con la perspectiva adecuada, a la otra hoja de la puerta, también de veintidós cuarterones, que se halla abatida tras el muro de la pared del fondo, a espaldas del retrato de la menina Isabel de Velasco, en cuya anchura incluiría a la Sefira nº 7, Netzach, la Victoria, la Eternidad...
Es, en definitiva, una Puerta de cuarterones castellanos cuya naturaleza oculta reivindicaría a la mismísima Torah oral, es decir; aquélla que fue transmitida oralmente y no fue escrita, de modo que el Aposentador José Nieto, en su espacio compositivo, encarnaría el poderoso mensaje de la Kabala; un nexo que el pintor español mantuvo velado ante la ortodoxia de su época.
Como bien se entiende ahora, los veintidós cuarterones de la Puerta no sólo cumplen disfrazados su función decorativa, sino que representan una perfecta anfibología de la identidad histórica de España, que una vez borrada toda su entereza católica, demuestran que a esta corte, empujada a lo prohibido para proteger a la Infanta y asegurar la supervivencia del Imperio, la fe oficial no le bastaba; y es aquí donde el lienzo deja de ser una oda a los Austrias para convertirse, colgado en el corazón del palacio más católico de la cristiandad, en el testimonio más evidente de su vulnerabilidad y desesperación
 |
|
|
Y aunque este tipo de Puerta no fuese uno de los motivos más recurrentes en la pintura del Barroco, sin embargo, estos 22 cuarterones simbolizan, pues, 22 fuerzas o letras hebreas que dan acceso a la totalidad del conocimiento, y su presencia, como elemento de la arquitectura tradicional española, evoca la velada añoranza judía rebosante de significado religioso, que, Velázquez, al medio abrirla, no solo permite el paso de la luz física, sino que activa su protección, por lo que esta Puerta se convierte en un pentáculo diseñado para detener el infortunio que perseguía a los Austrias.
Ante esta proposición, la familia real española demandaba más que ayuda en el año 1656.
|
Otros, de quien hace mencion el P. Benito Pereyra en el libro primero de su Comento sobre el Genesis, discurriendo que desde la venida de Christo hasta el fin del mundo, correria igual espacio de tiempo, que desde la Creacion hasta el Diluvio, pronosticaban la ruina del Orbe para el año 1656 de nuestra Redencion [2]. |
Una Profecía bíblica, a la cual temer, en pugna con el orden planetario, y que hacía alusión, ni más ni menos, al año 1656, el mismo año en el que fueron pintadas Las Meninas.
Velázquez eligió, pues, su propio taller, el Cuarto del Príncipe Baltasar Carlos, y no sólo para inmortalizarlo en su pintura, sino para transformarlo en un escenario de sanación para poner fin al mal recuerdo, de luto y desgracia; una circunstancia que trae a la memoria la décima plaga, en la que murió el primogénito del faraón después de que Moisés ordenara, por mandato de Dios, pintar las jambas, y el dintel de las puertas de sus casas con la sangre de un cordero para la protección de los hebreos; pero en este óleo con la finalidad de que el ángel de la muerte pasara de largo, y no volviera a entrar en la Habitación donde se alojó el primogénito del rey Felipe IV.
De manera, que el propio lienzo de Las Meninas se convierte en un mecanismo de protección para blindar la fortuna de los Austrias ante la adversidad, aunque, irónicamente, el rey que reinó años más tarde, Carlos II, se le llamó El Hechizado, simbolizando, pues, el quebranto de los esfuerzos humanos por revertir la extinción dinástica de los Austrias españoles.
 |
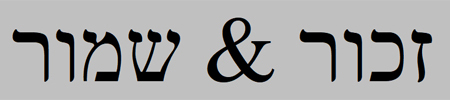 |
|
|
La principal misión de Diego Velázquez en la trama de Las Meninas fue recordar el fracaso dinástico por la muerte del Príncipe Baltasar Carlos, cuya ausencia motivó la creación de la obra en el mismo lugar donde se hospedó en el Alcázar de Madrid, y, pictóricamente, custodiar a la Infanta Margarita con un escudo de protección para ahuyentar todo mal presagio.
Y llegado el momento oportuno, en cualquier ritual de Kabala Práctica se utilizan ciertos textos sagrados para la invocación, y, necesariamente, el lugar debe estar consagrado al Este, al igual que el óleo de Las Meninas lo está respecto a la orientación física de la Habitación del Príncipe del Alcázar de Madrid:
La pared del fondo, donde se sitúa la Puerta de 22 cuarterones; es el Este.
Los 22 cuarterones de la Puerta guardan una estrecha relación con cada una de las 22 letras cuadradas del alefato.
La Puerta se convierte, pues, en el Hejal, היכל, el armario sagrado, situado al Este en las sinagogas, donde se guardan los rollos de La Torah.
Esta Puerta de madera representaría, entonces, una metáfora pictórica del libro más sagrado del pueblo hebreo: La Torah.
Esta Puerta, al estar orientada al Este y simbolizar La Torah, se convierte en la fuente de la autoridad espiritual del ritual, y no sólo como un talismán, sino que es la encarnación de la ley divina que protege a todo el espacio de la sala.
Hablamos, pues, de una Puerta de madera de 22 cuarterones medio abierta sobre el hombro izquierdo de la Infanta Margarita, que, como talismán, equivaldría, de manera palmaria, a las 22 letras del libro de la Ley escrita por Moisés.
22 letras que equivalen a los ladrillos de los que se sirvió el Arquitecto Divino para la construcción del mundo.
3 letras madres + 7 letras dobles + 12 letras simples = 22 letras hebreas
 |
Y todos están unidos, uno con el otro.
|
|
|
La organizada disposición de los 22 cuarterones, alineados con la perspectiva geométrica de Las Meninas, sintoniza con una fórmula de activación que se halla en el capítulo sexto, versículo quinto, del Sefer Yetzirah, con el propósito de contrarrestar la tragedia pasada, y proteger a la Infanta Margarita ante la adversidad, a modo de talismán, garantizando así la continuidad de su linaje [3]:
|
שלשה כל אחד לבדו עומד אחד מזכה ואחד |
 |
Tres se mantienen solos:
Siete, tres contra tres, y una ley decide entre ellos.
Doce se mantienen en guerra:
Y Dios, Rey fiel, gobierna sobre todos ellos desde su santa morada por los siglos de los siglos.
Uno sobre tres, tres sobre siete, siete sobre doce, y todos unidos, uno con el otro. |
|
|
Aunque la traducción literal de שני הנקבים es dos orificios, sin embargo, en la lectura del Sefer Yetzirah se entiende, pues, dos ojos; una explicación de acuerdo con la creencia de que los ojos y la boca tienen el poder de matar o causar daño mediante el mal de ojo o una maldición, de manera, que el significado de esta frase advierte del poder destructivo de una mirada o una palabra.
 |
|
Sefer Yetzirah - Capítulo 6:5 |
De acuerdo con el Sefer Yetzirah, estos doce órganos vitales representan en esta pintura la idea central de esta protección simbólica, de modo, que los 22 cuarterones de la puerta están organizados para defender a la Infanta Margarita con una poderosa salvaguarda.
Hacer mal de ojo, y dañar a otro con la vista por haber en ella infección, se refiere a una creencia popular supersticiosa capaz de causar daño, desgracia o enfermedad a otra persona con sólo mirarla, a menudo por envidia, es decir; el mal de ojo no se basa en una enfermedad real, sino en la creencia de que se transmite una energía negativa a través de la vista.
En el tratado de fascinación o de aojamiento D. Enrique de Aragón, marqués de Villena, 1384-1434, advierte que en el aojar intervienen dos elementos de sugestión: la mirada y la palabra.
|
E cuidan muchos que las palabras dañan en esto más que el catar, porque veen que, si alguno mira a otro que le bien paresca o lo alaba de fermoso o de donoso, luego paresca daño en él de ojo, siquier de fasçinaçión. E aquí deven entender, sana consideraçión mediante, que la causa d'esto es que aquel que alaba la cosa mirada, pues se d'ella paga, paresçe en esa ora que mira más fuerte, firme e atentamente que otra, toda la faz visual dirigiendo, fingiendo e ocupando en aquel catar. Esto faze mayor e más impresión paresçida e aquel dezir o loar non añade fuerça en el daño, más significa la atençión del catar. |
Está documentado, pues, que desde el siglo XVI la familia real española venía utilizando ciertos amuletos y talismanes para proteger a los infantes, que por su edad eran las víctimas más propicias a este tipo de hechizos, que en el caso de esta pintura, y, dada la tierna edad de la Infanta Margarita, fue necesaria la providencia de una magia que ahuyentara malos espíritus, y la protegiera del mal de ojos con la ayuda de un exorcismo hebreo de dos mil años de antigüedad, lo que explica que, en la época de Diego Velázquez, la línea roja entre la fe, la magia y la superstición era muy difusa.
|
|
|
|
|
Letra doble |
Nombre |
Concepto |
Planeta |
Versión Gra |
 |
Dalet |
Semilla |
Sol |
Nariz derecha |
|
המליך אות ד' בזרע |
Hizo la letra Dalet, ד, rey sobre la Semilla. |
|
|
וקשר לו כתר |
Y le ató una corona, |
|
|
וצרפן זה בזה |
y combinó una con otra, |
|
|
וצר בהם |
y con ellas formó |
|
|
חמה בעולם |
el Sol en el universo, |
|
|
יום שלישי בשנה |
el Martes en el año, |
|
|
ונחיר ימין בנפש |
la fosa nasal derecha en el alma, |
|
|
זכר ונקבה׃ |
masculino y femenino. |
Sefer Yetzirah - Capítulo 4:10
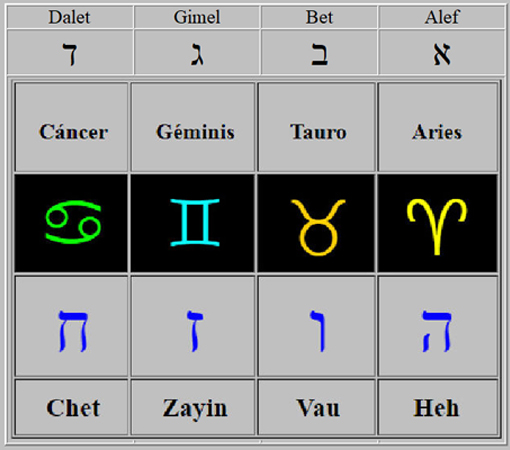
Aparentemente la puerta de 22 cuarterones se pinta sobre el hombro izquierdo de la Infanta Margarita de Austria, que había nacido, pues, el 12 de Julio del año 1651 en Madrid, luego ella era del signo de Cáncer, y su planeta personal la Luna.
Veamos:
Desde su origen, las 22 letras que aparecen en manuscritos o impresas en cualquier libro hebreo se denominan:
 |
|
|
La traducción de PUERTA en hebreo es DELET, דֶּלֶת, y, a su vez, DALET, דָּלֶת, es el nombre de la cuarta letra del Alefato, y, en estricto orden, de acuerdo con la división de la pared del fondo en 12 partes iguales, la PUERTA de 22 cuarterones ocupa la cuarta posición en el Zodiaco en el signo de CÁNCER, cuyo planeta regente es la LUNA.
 |
En 1613, Francisco de Quevedo Villegas, 1580-1645, propone, en sus Lágrimas de Hieremías castellanas, un aforismo moral sacado del primer alfabeto de Jeremías denominado DALET [4].
|
DALET
En la Ciudad donde no ſe ſirve a la Religion no ay puerta en pie; las calles se enlutan; los Sacerdotes lloran; todo perece, porque ella es la defensa de las republicas y el fundamento del gobierno político; porque ſi Dios no guarda la Ciudad en vano trauaxan los que la guardan. |
Un aforismo que pone de manifiesto la relación de la Puerta con la Religión, y esta, a su vez, con el fundamento del gobierno político.
El tiempo, como eterno nómada, Velázquez lo asocia con la cadencia de lo cotidiano en la ruta celeste de arriba, que es puntual con los avisos de abajo, y los de abajo con los de arriba, a fin de rememorar la efeméride de ciertas jornadas a lo ancho de la pared del fondo.
 |
|
|
|
Esta sincronicidad cronológica dota a Las Meninas de una función ritual activa y personalizada, y es el golpe de efecto de su estructura espacial, en donde es de resaltar la jornada del Apóstol Santiago, día en el que fue bautizada la Infanta Margarita por el Nuncio de su Santidad en la Capilla Real, además de la marca del 24 de Junio, San Juan Bautista, sugerida en el suelo del pasillo con pinceladas de luz muy intensa sobre la vertical de su reposada mano izquierda, lo que hace posible considerar la consagración de la Infanta como princesa heredera, y, de puertas adentro, reconocida sucesora del trono de Castilla.
 |
|
|
Al igual que las manillas del reloj miden el tiempo, mostramos, pues, el tránsito, de derecha a izquierda, de la fugaz línea temporal que da sentido narrativo a esta obra maestra, y, con estricto orden, ilustra la posición de los personajes, objetos o marcas en fechas concretas.
Y, ante este tipo de lectura, se desvela gráficamente la salvaguarda de la Infanta:
La marca del cumpleaños de la Infanta, el 12 de Julio sobre su brazo izquierdo,
el día de su santa patrona, el 20 de Julio en la posición correcta de 366 días de un año bisiesto
y la del patrón del reino de España; Santiago apóstol, el 25 de Julio.
Y nos hacemos eco del comentario de Giovanni Pico della Mirandola de su libro: Cabalistarum selectiora obscurioraque dogmata. Venecia. M D LXIX, donde hace alusión al Apocalipsis 21:12, y señala al signo de Cáncer como la puerta solsticial por donde las almas bajan del cielo a la tierra, es decir, alude al lugar concreto por donde el alma humana se incorpora a la vida en el momento de su nacimiento.
|
שערים שלשה ממזרח שערים שלשה מצפון שערים שלשה מנגב ושערים שלשה ממערב׃
Al oriente tres puertas; al aquilón tres puertas; al mediodía tres puertas; al poniente tres puertas.
Apocalipsis 21:13 |
 |
|
Códice de Fernando I y doña Sancha. 1047
Beato de Liébana. Madrid, Biblioteca Nacional |
Este personaje, que podría ser un ángel, lleva sin embargo el nombre que corresponde al apóstol San Andrés, relacionado con el zafiro, y con el signo del Zodíaco Cancer, y conecta directamente con la insigne Orden del Toisón de Oro fundada por Felipe el Bueno bajo el patronazgo de este apóstol, en el mismo día que celebró sus terceras nupcias con la Infanta Isabel de Portugal, el 10 de Enero de 1429 en la ciudad de Brujas.
La bula de confirmación de la Orden y de aprobación de sus constituciones y ordenanzas las expidió el papa Eugenio IV el 7 de Septiembre de 1433.
|
|
|
|
Felipe IV de Austria, en su condición de Jefe y Soberano de la Orden del Toisón de Oro, y, tal y como había establecido su fundador, Felipe el Bueno, Duque de Borgoña, estaba obligado a mantener la fidelidad que los Caballeros debían guardar a la Santa Iglesia Romana.
Y hecha esta aclaración, habría que recordar que la superstición era una de las dinámicas más activas y privadas de una monarquía, heredera de reinos e imperios, que en el año 1656 desafiaba su futuro en la persona de la Infanta Margarita de Austria.
|
|
|
Diego Velázquez. Madrid, Fundación Casa de Alba. 1655 |
 |
|
|
Y hablando de prevención de enfermedades, observemos, pues, en un retrato de la Infanta Margarita de Austria, pintado por Diego Velázquez un año antes de Las Meninas, una protección mágica, de una higa de azabache prendida a la altura de su hombro izquierdo, que permite asumir que tanto la higa como la puerta de 22 cuarterones son talismanes que cumplen con el mismo propósito apotropaico para la salvaguarda de la Infanta, heredera al trono en ese momento.
|
La esperanza que se prolonga, es tormento del corazón; mas el Árbol de Vida es el deseo cumplido.
תוחלת ממשׁכה מחלה־לב ועץ חיים תאוה באה׃
Proverbios 13:12 |
A pesar de que estas ideas traigan a la memoria el mal recuerdo de una sociedad intolerante, que desaprobaba lo que se ha tratado en este apartado, sin embargo, justifican la importancia del mensaje de Las Meninas.
Como dijo Baruch de Spinoza:
La causa que hace surgir, conservar y fomentar la superstición es, pues, el miedo.
¿Es éste el punto de partida para poder explicar el acoso político que sometía Francia a España, y todo por el amor que profesaban unos padres a su hija heredera de sus muchos y extensos reinos?
Aunque la paz no estaba totalmente asegurada, no olvidemos que estaba en juego, además, la permanencia de los Austrias en España.
El sistema de medidas
Operaremos, pues, con el
Pie Real de 0,279 m., y aunque
sea una desviación histórica levemente mayor que la vara de Burgos de tres pies
de 0,2786 m., utilizada por veinticinco provincias en la época de Velázquez, sin
embargo, esta elección es un requisito indispensable para que
el estudio de la Geometría de Las Meninas
culmine en un descubrimiento.
La diferencia entre ambos tamaños, de 0,279 m. y 0,2786 m., es de 0,0004 metros, un margen extremadamente pequeño que no supone, pues, una anomalía en el cálculo matemático, ya que demostramos que el tamaño de un Pie Real de 0,279 m. escala las medidas geométricas longitudinales y proporcionales con una métrica exacta.
O sea, que el rescate del tamaño original del Pie Real ha recuperado el instrumento de medición, que hace valer una exactitud que permite operar con una tolerancia de una diezmilésima de unidad, es decir, 0,0001 de unidad, lo que se traduce en un valor de 0,002066 milímetros [5].
|
|
X = 20,666666 x 0,0001 / 1 = 0,002066 milímetros.
En consecuencia, este minúsculo margen de seguridad de 0,002066 milímetros representaría el rigor matemático de cualquier dato numérico que especifiquemos, y que propiamente hablando equivale a esta cantidad de micras:
|
|
X = 0,002066 milímetros x 1000 micras / 1 milímetro = 2,066666 micras [6].
Un dato que basta para comprender la sutileza de esta escala, donde el grosor del cabello humano más fino ronda las 17 micras, y que un glóbulo rojo tiene un diámetro de apenas 5 a 7 micras.
Operamos, pues, en una dimensión donde la materia es casi etérea, y medimos con la ayuda de una cuadrícula de trabajo que, como herramienta geométrica, revela dos cuestiones fundamentales;
el mensaje oculto de Las Meninas,
y el tamaño exacto de este lienzo.
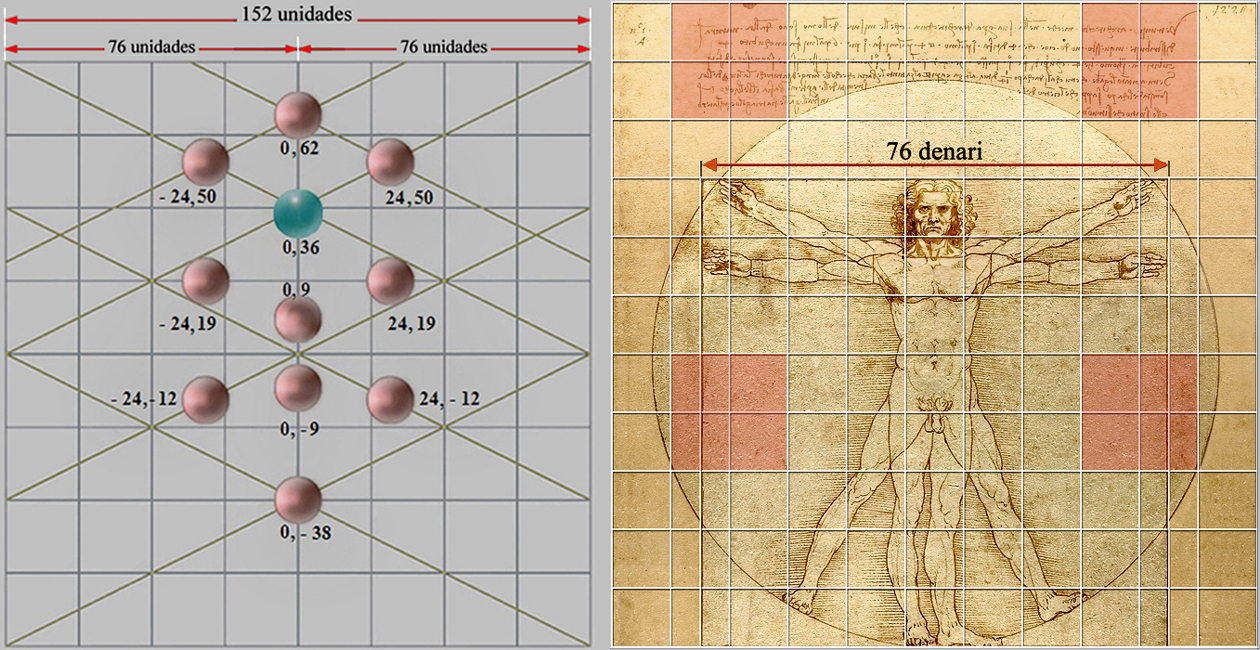
No obstante, en el lado del cuadrado que inscribe la altura y anchura del Hombre de Vitrubio se emplea el número 76, nos referimos, pues, a una cantidad contenida dos veces en el tamaño del lado de la cuadrícula de trabajo de 8 x 8 cuadrados que utilizamos para analizar el óleo de Velázquez.
 |
|
|
Leonardo da Vinci también utilizó, pues, una cuadrícula de de 8 x 8 cuadrados, donde cada subcuadrado mide 9,5 denari de lado, lo que multiplicado por 8 sumaría un total de 76 denari florentinos, por tanto, en el papel, la altura del dibujo del Hombre de Vitrubio mediría:
76 denari x 0,243055... cm. por denaro = 18,472222... cm.
Y dada la antigüedad de Las Meninas, se entiende, pues, que cualquier dato acerca de su formato requiere el visto bueno de las reglas de Geometría, y el empleo de números enteros y racionales, junto a sus equivalentes en el sistema de medidas castellano, para garantizar el cálculo aritmético.
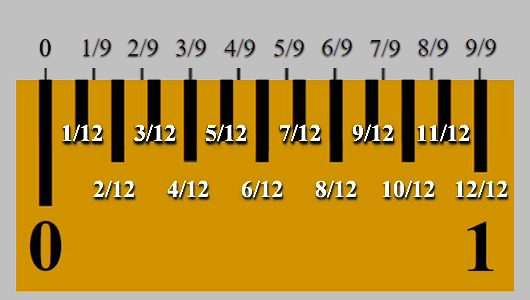
Presentamos, pues, LA UNIDAD, cuyo tamaño, basado en la pulgada castellana y el milímetro, es exactamente el soporte técnico que respalda el análisis de la estructura geométrica de esta pintura.
 |
|||||||
| 9 partes | Unidades | 9 partes | Pulgadas | Milímetros | |||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 | |
| 8/8 | = | 1 | 8/9 | = | 0,888888 | 20,666666 | |
| 7/8 | = | 0,875 | 7/9 | = | 0,777777 | 18,083333 | |
| 6/8 | = | 0,75 | 6/9 | = | 0,666666 | 15,5 | |
| 5/8 | = | 0,625 | 5/9 | = | 0,555555 | 12,916666 | |
| 4/8 | = | 0,5 | 4/9 | = | 0,444444 | 10,333333 | |
| 3/8 | = | 0,375 | 3/9 | = | 0,333333 | 7,75 | |
| 2/8 | = | 0,25 | 2/9 | = | 0,222222 | 5,166666 | |
| 1/8 | = | 0,125 | 1/9 | = | 0,111111 | 2,583333 | |
|
|
| Unidad |
Pulgadas por unidad |
Milímetros por
unidad |
|
1 |
8/9 = 0,888888... |
20,666666... |
|
|
| UNIDAD | PULGADA | MILÍMETRO | ||||
Este flamante sistema de medición y proporción gestiona magnitudes presentes en esta pintura que, de otra manera, pasarían desapercibidas; no obstante, por su condición de patrón de medidas, define, pues, un nuevo modelo de medición denominado LA UNIDAD, que, además de medir Geometría, desbloquea y valida la interpretación de capas ocultas llenas de significado.
Como herramienta de conversión, la consistencia de LA UNIDAD supera a cualquier patrón de longitud conocido; de modo, que el potencial de este hallazgo abre nuevas vías para la investigación, ya que, como número conversor, define un modelo no antropomórfico de equivalencias entre los diferentes métodos de medición a nivel mundial.
| PATRÓN DE MEDIDA | ORIGEN | MILÍMETROS | FRACCIÓN EXACTA | UNIDADES | ||
| METRO | 1000/1 | = | 1000 | 1500/31 | = | 48,387096... |
| RASA ANDALUSÍ | 2511/3 | = | 837 | 81/2 | = | 40,5 |
| BRAZO FLORENTINO | 1750/3 | = | 583,333333... | 875/31 | = | 28,225806... |
| CODO REAL EGIPCIO | 2100/4 | = | 525 | 1575/(31×2) | = | 25,403225... |
| SUHUY REAL PRECOLOMBINO | 2100/4 | = | 525 | 1575/(31×2) | = | 25,403225... |
| SHAKU JAPONÉS | 1209/4 | = | 302,25 | 453,375/31 | = | 14,625 |
| PULGADA ESTÁNDAR INGLESA | 1600,2/63 | = | 25,4 | 381/(31×10) | = | 1,229032... |
| PULGADA EXACTA INGLESA | 1600/63 | = | 25,396825... | 800/(31×21) | = | 1,228878... |
| PULGADA INGLESA 8π | 8 × 198/63 | = | 25,142857... | 12π/31 | = | 1,216589... |
| PULGADA CASTELLANA | 93/4 | = | 23,25 | 9/8 | = | 1,125 |
| LA UNIDAD | 62/3 | = | 20,666666... | 31/31 | = | 1 |
|
|
Estos diferentes PATRONES DE MEDIDAS, distantes en tiempo y espacio, están interconectados a través de LA UNIDAD, donde el número 31, o sus múltiplos como común denominador, ejerce de catalizador de todos estos sistemas metrológicos, al igual que el 8 en relación con la pulgada castellana.
Dentro de este grupo de patrones de medidas, resaltaríamos el Shaku japonés por su lejanía geográfica, ya que su equivalencia exacta con 13 pulgadas castellanas, 13 × 23,25 = 302,25 mm., confirma que el 13 es un factor determinante de 1209, y, aparte de esta pureza matemática, el año lunar se calcule con 13 lunas de 28 días cada una, lo que hace un total de 364 días del ciclo natural.
En consecuencia, si la arquitectura del Japón y la pintura de Velázquez beben del mismo origen aritmético, entonces hablamos del código genético que permite asegurar que una palanca en la España del siglo XVII, y otra en el Japón del shogunato Edo hacia 1650, se apoyaban en el mismo punto, donde 78 pulgadas castellanas equivalen, pues, a 6 Shakus, o sea, 1 Ken.
Es significativo, pues, que en épocas diferentes autores establecieron un puente entre las matemáticas, la música y el macrocosmos en la búsqueda de una armonía universal, lo que constituye el antecedente histórico que da contexto a LA UNIDAD.
|
Pitágoras |
(570 a. C. - 490 a. C.) |
|
Alberto Durero |
(1471-1528) |
|
Vitrubio |
(80 a. C. - 15 a. C.) |
Johannes Kepler |
(1571-1630) |
|
|
Luca Pacioli |
(1445-1517) |
Robert Fludd |
(1574-1637) |
|
|
Leonardo da Vinci |
(1452-1519) |
Isaac Newton |
(1643-1727) |
Especial mención merece Isaac Newton, que mantenía que la medida del Codo Sagrado no era una medida arbitraria, sino una constante armónica que traducía las leyes de Dios y del cosmos a la escala humana; o sea, una métrica universal que abogaba por un universo afinado bajo un patrón de medida único que conectaba a la ciencia, el arte y la divinidad; sin embargo, para nuestro interés, se trataba de una teoría arrumbada desde hacía varios siglos que preservaba el dato definitivo que esperaba ser descubierto [7].
Y este círculo cierra gracias al valor de 20,666666... milímetros de LA UNIDAD que emana de la proporción sesquioctava 9/8, equivalente al intervalo tonal básico de la música pitagórica, que, trasladada a la escala métrica, se revela como una cualidad permanente de la realidad, ajena al contacto entre culturas, y, como constante armónica, traduce las leyes del sonido y del cosmos al lienzo de Velázquez, constituyendo, pues, una alternativa de precisión absoluta para todo procedimiento que exija el rigor del orden y la medida.
| Fracción | Milímetros | Unidades | Pulgadas | Fracción | Milímetros | Unidades | Pulgadas | |||||||
| 62/3 | = | 20,666 | 31/31 | 82,666/93 | 28/3 | = | 9,333 | 14/31 | 37,333/93 | |||||
| 60/3 | = | 20 | 30/31 | 80/93 | 26/3 | = | 8,666 | 13/31 | 34,666/93 | |||||
| 58/3 | = | 19,333 | 29/31 | 77,333/93 | 24/3 | = | 8 | 12/31 | 32/93 | |||||
| 56/3 | = | 18,666 | 28/31 | 74,666/93 | 22/3 | = | 7,333 | 11/31 | 29,333/93 | |||||
| 54/3 | = | 18 | 27/31 | 72/93 | 20/3 | = | 6,666 | 10/31 | 26,666/93 | |||||
| 52/3 | = | 17,333 | 26/31 | 69,333/93 | 18/3 | = | 6 | 9/31 | 24/93 | |||||
| 50/3 | = | 16,666 | 25/31 | 66,666/93 | 16/3 | = | 5,333 | 8/31 | 21,333/93 | |||||
| 48/3 | = | 16 | 24/31 | 64/93 | 14/3 | = | 4,666 | 7/31 | 18,666/93 | |||||
| 46/3 | = | 15,333 | 23/31 | 61,333/93 | 12/3 | = | 4 | 6/31 | 16/93 | |||||
| 44/3 | = | 14,666 | 22/31 | 58,666/93 | 10/3 | = | 3,333 | 5/31 | 13,333/93 | |||||
| 42/3 | = | 14 | 21/31 | 56/93 | 9/3 | = | 3 | 4,5/31 | 12/93 | |||||
| 40/3 | = | 13,333 | 20/31 | 53,333/93 | 8/3 | = | 2,666 | 4/31 | 10,666/93 | |||||
| 38/3 | = | 12,666 | 19/31 | 50,666/93 | 6/3 | = | 2 | 3/31 | 8/93 | |||||
| 36/3 | = | 12 | 18/31 | 48/93 | 4/3 | = | 1,333 | 2/31 | 5,333/93 | |||||
| 34/3 | = | 11,333 | 17/31 | 45,333/93 | 3/3 | = | 1 | 1,5/31 | 4/93 | |||||
| 32/3 | = | 10,666 | 16/31 | 42,666/93 | 2/3 | = | 0,666 | 1/31 | 2,666/93 | |||||
| 30/3 | = | 10 | 15/31 | 40/93 | 0/3 | = | 0 | 0/31 | 0/93 |
|
|
Entender el concepto de la unidad es fundamental para cualquier ciencia, ya que es la base que permite medir, comparar y cuantificar una cantidad en una determinada magnitud física.
Dentro del estándar de la física moderna, LA UNIDAD de 20,666666... milímetros puede definirse formalmente a través del tiempo exacto que la luz tarda en recorrer dicha distancia; que queda establecida, por tanto, por la longitud de la trayectoria recorrida por la luz en el vacío durante un intervalo de tiempo de 0,0000000000689366... segundos:
|
|
Esta validación científica logra que esta constante universal trascienda su contexto histórico, ya que define un estándar de precisión tan exacto que, en términos metrológicos, se puede afirmar que LA UNIDAD ha sido plenamente realizada.
Y es del todo cierto que LA UNIDAD precede a todos los sistemas de medida aquí comparados, ya que este hallazgo deriva de principios matemáticos y geométricos inherentes a la estructura misma de la realidad, mientras que el pie castellano, el metro francés, el brazo florentino o la pulgada estándar inglesa son unidades de medida definidas por estrategias políticas en momentos históricos determinados.
Por su naturaleza atemporal, la trascendencia de LA UNIDAD reside, no obstante, en el marco legal; ya que quien imponga un estándar de medidas, controla con ventaja la economía, el comercio, la arquitectura y, en última instancia, la realidad física de un Estado, la cual Diego Velázquez valida en su lienzo codificando la logística física y espiritual del Imperio Español.
La necesaria precisión en la investigación de Las Meninas sugiere que el análisis convencional no siempre ha atribuido a los artistas de esta época un conocimiento profundo de las Matemáticas o de la Geometría, pero sí del simbolismo.
Así, la Geometría y LA UNIDAD se convierten en el garante absoluto de un enigma donde la precisión Matemática y el simbolismo convergen para revelar la totalidad del mensaje del artista
El Árbol de la Vida
Explicar algo, que hasta su descubrimiento no existía de forma
conocida, ha supuesto un esfuerzo, que, finalmente, se ha materializado en
la posición de
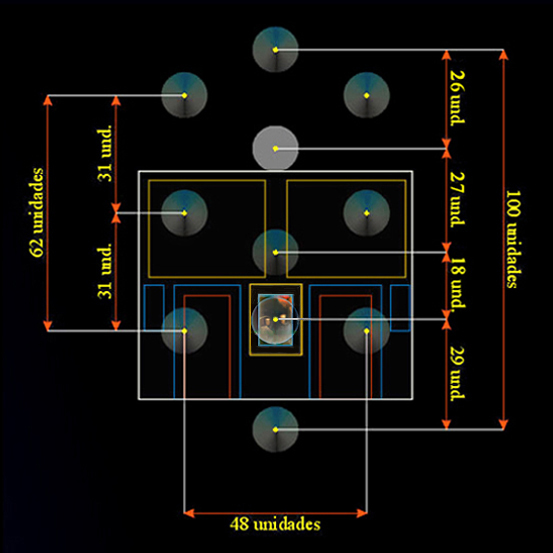
10 + 1 esferas
en coordenadas de números enteros en una rejilla
de trabajo de 152 unidades
de lado, y,
no obstante,
estas
esferas, huéspedes del
espacio aéreo de la Habitación del Príncipe,
se asientan sobre un mapa de
23104
coordenadas
posibles,
que
atesora,
bajo el logrado naturalismo
de esta
obra maestra,
una experiencia artística extraordinaria.
Al multiplicar las 152 unidades del lado de la rejilla de trabajo por 1/1000 de LA UNIDAD de 20,666666... mm, obtenemos un valor conceptual de 3,141333...
Es decir, el despliegue geométrico del Árbol de la Vida de Las Meninas se detiene exactamente en el umbral del número Pi: 3,141592.., lo que demuestra que Velázquez fijó su trazado en la frontera misma de la perfección matemática.
 |
 |
|
|
Operamos, pues, en una gran cuadrícula graduada como soporte geométrico de los llamados diez Sefirot del Árbol Sagrado de la Vida, que consolida la simetría del escenario pictórico, y confirma, además, que en una antigua restauración el tamaño de esta pintura fue alterado [8].
En la mitad superior, donde todo el mundo percibe el aire pintado en este óleo, Diego Velázquez concibió, pues, el germen de luz primigenia de la emanación del Árbol de la Vida, cuyo destello se irradia a través de sus senderos en los demás Sefirot, es decir, una idea comparable, pues, con el famoso argumento de La Primera Causa defendido por Tomás de Aquino en el siglo XIII, que el cristianismo asoció con Dios, en el que todo movimiento requiere un primer motor, que, en el caso de Las Meninas, ese motor es la Luz de la Sefira nº 1, Kether, la Corona.
El primer Mundo, el plano de la emanación, constituido por las tres primeras Sefirot:
Olam ha Atzilut - עולם האצילות
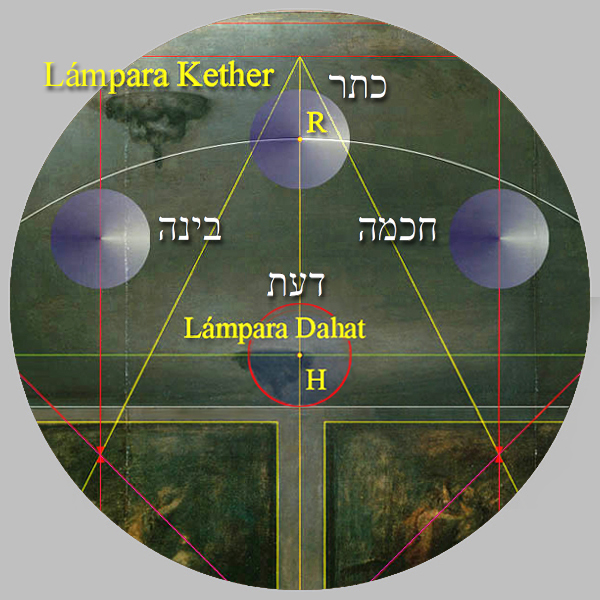 |
Primer nivel del Árbol Sagrado
עולם אצילות - Olam Atzilut |
|
|
En la primera Sefira Kether se descubre el Espíritu, la Voz y la Palabra del Dios viviente, que consolidarían, pues, al Espíritu Santo, aunque para el caso del pintor Velázquez esta Sefira aludiría al punto culminante de la secreta misión que ha llevado a cabo.
|
Verano de 1977, Jorge Luis Borges:
La primera emanación se llama la Corona y es comparable a un rayo de luz que surge del En soph, un rayo de luz que no lo disminuye, un ser ilimitado al que no se puede disminuir. De la Corona surge otra emanación, de ésa, otra, de ésa, otra, y así hasta completar diez. Cada emanación es tripartita. Una de las tres partes es aquella por la cual se comunica con el Ser Superior; otra, la central, es la esencial; otra, la que le sirve para comunicarse con la emanación inferior.
Las diez emanaciones forman un hombre que se llama el Adam Kadmon, el Hombre Arquetipo. Ese hombre está en el cielo y nosotros somos su reflejo. Ese hombre, de esas diez emanaciones, emana un mundo, emana otro, hasta cuatro. El tercero es nuestro mundo material y el cuarto es el mundo infernal. Todos están incluidos en el Adam Kadmon, que comprende al hombre y su microcosmo: todas las cosas. |
De acuerdo con la Kabala, más allá, y por encima de toda contemplación humana, está Dios, tal y como es en sí mismo, el incognoscible Ain Sof, אין סוף, y su luz divina, Aur, אוֹר.
|
|
|
|
|
Ain Sof Aur - Luz Infinita |
Aclaremos, pues, que el contacto del tiento, que sujeta Diego Velázquez en su mano izquierda, con el centro de la primera Sefira Kether se produce en el punto primigenio denominado n'kudoh r'shonoh, נקודה ראשונה, y conocido también como n'kudoh p'shutoh, נקודה פשוטה.
Esta disposición explica que el pintor, al apuntar el tiento hacia el techo de la Habitación del Príncipe, da entrada a un mundo espiritual con el fin de revelar lo invisible, mientras que el pincel dirigido hacia el suelo en su mano derecha da fe, en respuesta, de que se nace de la tierra, y que, después de la liberación del alma, el cuerpo a ella retornará.
Con esta reivindicación, admitimos pues, que el pintor interioriza su experiencia mística aferrándose a Dios en estado de devekut, דבקות, de modo que, el tiento, en este punto R, revela el vacío de la luz divina como causa de la inspiración artística.
|
|
|
|
La coordenada del punto Q -0,5 : [- 36, - 0,5], se acomoda a media altura de la arista lateral izquierda de la pared del fondo, que se halla totalmente oculta tras el larguero de madera del Gran Bastidor en el primer plano.
La distancia geométrica y física entre el punto Q -0,5 y el punto S : [0, - 63] es igual a la que hay entre el punto Q -0,5 y el punto R.
|
Q -0,5 S = Q -0,5 R |
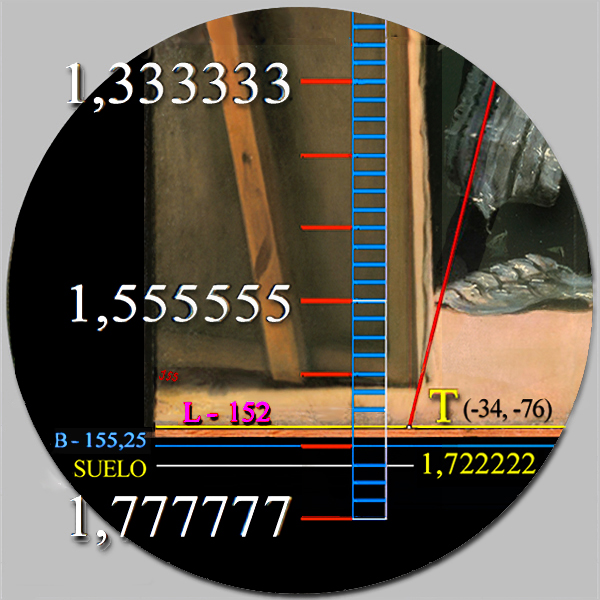
El trazado del tiento de madera discurre desde el punto T : [- 34, - 76], situado en la base del lienzo, en la intersección con el Límite de la rejilla de 152 unidades, hasta el centro de la emanación divina más elevada, el punto R : [0, 62], que representa, pues, el centro de la Sefira nº 1 Kether, La Corona.
 |
|
|
|
En el trazado de este vector, pues, hacemos una parada de rigor en el punto W : [- 17, - 7] , y observamos, que esta coordenada W se encuentra situada, exactamente, en el punto medio de su ascenso, y justo debajo de la vertical del enganche de la Lámpara Kether.
|
TW = WR |
Geométricamente, esta certera vertical y horizontal a la altura de la nuez de la garganta del pintor son las dos formantes, abscisa y ordenada, de una inusual coordenada en el punto W, cuya función es servir de punto medio entre el ascenso del tiento hacia lo divino, en el centro de la Sefira nº 1, Kether, la Corona, y su anclaje en tierra a pie de lienzo.
El punto W es la única coordenada disponible, en este área de 144 unidades de altura, es decir; a 2,976 metros de los 3,18 metros de la altura actual del lienzo de Las Meninas.
Estamos analizando, pues, puntos concretos situados debajo del enganche para lámpara más elevado, y ha surgido de esta observación la prueba geométrica que ratifica la importancia de este punto W.
La probabilidad de que Velázquez haya situado, accidentalmente, la Sefira nº 1, Kether, la Corona, y la Sefira nº 8, Hod, la Gloria, que corresponde a la Cruz de Santiago, en las coordenadas exactas requeridas en el Árbol de la Vida, es de, aproximadamente, 1 entre 534 millones, lo que demuestra que la localización de estos dos puntos focales refuerza la intencionalidad compositiva del pintor.
Y ahora se entiende que el lienzo de Las Meninas no sólo es el resultado del estudio de una amplia gama de efectos del claro y oscuro de la luz, y de sus tonos grises, sino que tuvimos que buscar en ciertos libros prohibidos el origen de su velada inspiración; un esfuerzo que tomó sentido práctico gracias al hallazgo del Sefer Yetzirah, conocido también como el Libro de la Formación.
|
Estos son los Diez Sefirot de la nada: El aliento de Dios vivo, aliento del aliento, agua del aliento, fuego del agua. Arriba, abajo, sur, norte, este, oeste.
אלו עשר ספירות בלימה רוח אלהים חיים רוח מרוח מים מרוח אש ממים רום ותחת דרום צפון מזרח ומערב
Sefer Yetzirah 1:14 |
|
|
La Geometría Sagrada
Diego Velázquez, en el proceso creativo de su obra,
plantea una Geometría de
acorde a su época, que, como se puede comprobar, la altura del eje central del Árbol de la Vida de
Las Meninas corresponde, pues, a la hipotenusa AE de la base del
Triángulo Rectángulo Áureo de Kepler.
Y esta propuesta es posible porque la distancia entre el centro de la Sefira nº 1, Kether, La Corona: (0, 62) y el centro de la Sefira nº 10, Malkut, El Reino: (0, -38), mide, exactamente, 100 unidades, es decir; un múltiplo de 10 de acorde al punto (3) Latus AE 10 = 10 del análisis del Problema del triángulo áureo del año 1597 planteado por Michæl Mästlin, el maestro de Kepler.
 |
AE |
AD |
ED |
|
10 |
√61,803398... |
√125 - 5 |
|
|
10 |
7,861513... |
6,180339... |
|
|
MICHÆL MÄSTLIN |
|||
|
Φ |
√Φ |
1 |
|
|
1,618033... |
1,272019... |
1 |
|
|
100 |
78,615143... |
61,803398... |
|
|
DIEGO VELÁZQUEZ |
|||
|
|
|
Dos grandes tesoros tiene la Geometría; uno es el Teorema de Pitágoras, y, el otro, la división de un segmento en media y extrema razón:
Al primero lo podemos comparar a un montón de oro, y al segundo lo podemos llamar una piedra preciosa. |
|
Dos teoremas de infinita utilidad, y por lo tanto de gran valor, pero con una gran diferencia entre ellos. En cuanto al primero, porque los lados de un rectángulo pueden ser tan largos como la longitud de una línea recta, digo que has comparado correctamente esto con una masa de oro; y al segundo, sobre la sección proporcional, lo has llamado una gema. Porque es ciertamente hermoso en sí mismo, pero sin el primero no vale nada: sin embargo, hará avanzar aún más la ciencia cuando ya nos haya fallado, habiéndose adelantado hasta cierto punto, es decir, hasta la demostración y descubrimiento del lado decagonal y cantidades relacionadas.
IN CAPVT DVODECIMVM NOTAE AVCTORIS. Bearbeitet von Frankz Hammer. München. MCMLXIII. |
Poderosas palabras de Johannes Kepler, 1571-1630, astrónomo y matemático alemán, figura clave en la revolución científica, y principalmente conocido por sus leyes sobre el movimiento de los planetas en su órbita alrededor del Sol.
No obstante, estamos ante la demostración visual de la hipótesis que subyace tras el naturalismo de Las Meninas, hablamos, pues, de una estructura basada en la proporción áurea del Triángulo de Kepler, y cuya Geometría implica al Árbol de la Vida.
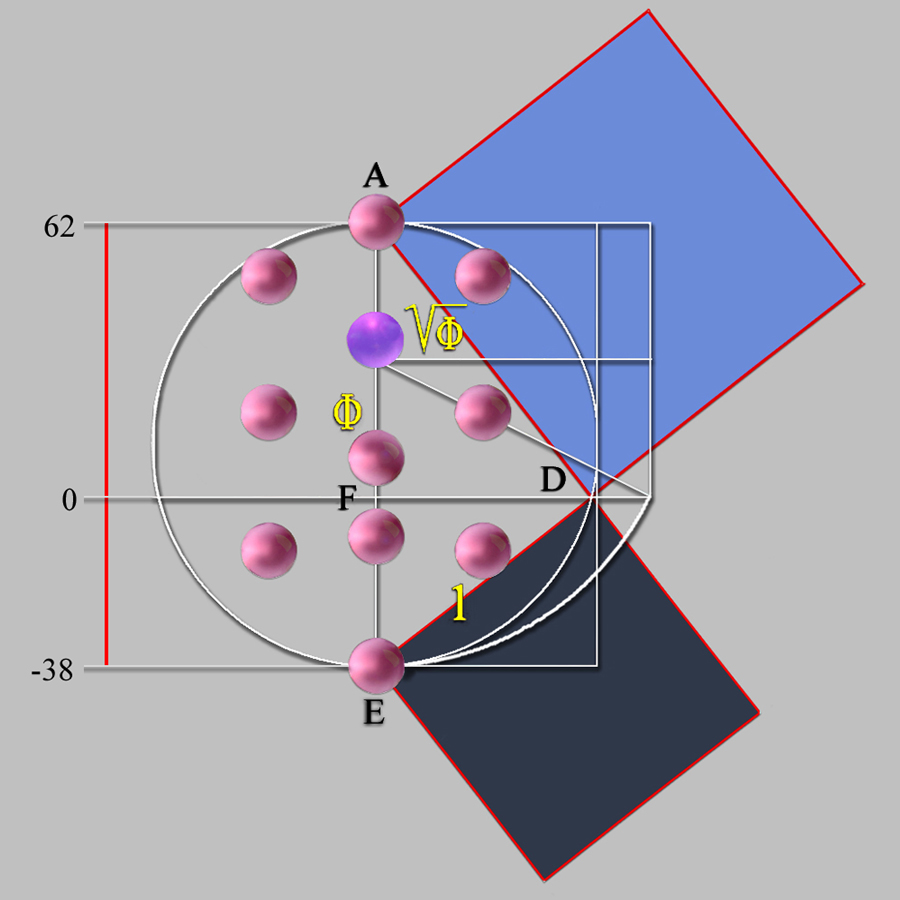 |
|
|
Si bien, en este renglón habría que subrayar, pues, ciertas cuestiones que justifican la elección de este tipo de Geometría áurea:
El punto F, en el triángulo de Kepler, está localizado en la misma posición que el centro de coordenadas E, es decir; en la posición del centro, (0, 0), de la Geometría de Las Meninas.
La distancia entre el centro de la Sefira nº 1, Kether, La Corona: (0, 62) y el centro de la Sefira nº 10, Malkut, El Reino: (0, -38), mide 100 unidades, es decir; un múltiplo de 10 de acorde al punto (3) Latus AE 10 = 10 del análisis del Problema del triángulo áureo.
Las medidas de los tamaños de los tres lados del triángulo áureo, que descubrimos en el aire de este lienzo, no sólo tratan de cifras, sino cantidades en unidades que son equivalentes, por tanto, a las pulgadas castellanas, y, por supuesto, a metros.
 |
|
|
| DISTANCIA |
AE |
AD |
ED |
AF |
FE |
|
| proporción Phi |
Φ |
√Φ |
1 |
1 |
1/Φ |
|
|
1,618033... |
1,272019... |
1 |
1 |
0,618033... |
|
|
| DISTANCIA |
AE |
Hipotenusa |
AD |
Cateto mayor |
ED |
Cateto menor |
AF |
FE |
|
| unidades |
100 |
78,615143... |
61,803398... |
62 |
38 |
||||
| pulgadas |
88,888888... |
69,880127... |
54,936387... |
55,111111... |
33,777777... |
||||
|
|
|
TAMAÑO TEÓRICO |
|
PROPORCIÓN PHI |
|
DIFERENCIA |
||||||||
|
AE = 100 unds. |
AF |
62 unidades |
÷ |
FE |
38 unidades |
≈ |
1,631578... |
0,013544... unds. |
≈ |
0,279909... milímetros |
||
|
Phi = 99,986456... unds. |
1 + √5 |
÷ |
2 |
≈ |
1,618033... |
|||||||
|
|
|
|
Una diferencia del vector AE respecto a Phi de 0,279909... milímetros.
Esta propuesta eleva el arte de la pintura de una mera técnica compositiva a un plano filosófico y metafísico, ya que la grandeza de Velázquez no reside sólo en su pericia manual, sino en su capacidad para sintonizar su obra con las leyes fundamentales que rigen la realidad y la percepción humana.
Una idea que conecta la esencia del pitagorismo con la creencia de que la realidad, el cosmos, el arte y la música, está regida por números y proporciones inmutables que el alma humana reconoce de forma innata como armonía y verdad.
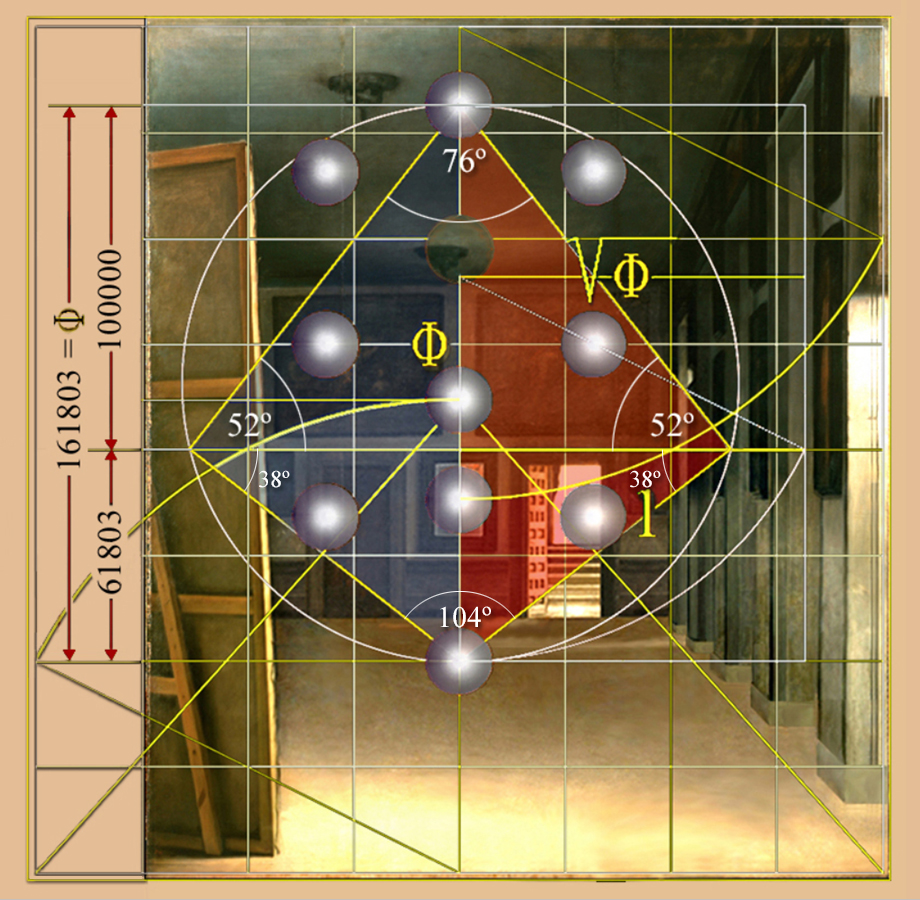 |
|
|
|
ÁNGULOS AGUDOS |
TOLERANCIA |
|||
|
52º ≈ 51,83º |
= | 51º 49′ 48′′ |
- 0,32... % |
|
|
38º ≈ 38,17º |
= | 38º 10′ 12′′ |
+ 0,44... % |
|
52º + 38º = 51,83º + 38,17º = 90º
Este análisis demuestra que la desviación de la proporción entre el tamaño del pilar del Equilibrio del Árbol de la Vida, distancia AE en la pintura y el número áureo Phi, Φ, es de tan sólo 0,279909... milímetros, una diferencia casi imperceptible a simple vista, lo que subraya la precisión geométrica de esta obra de Velázquez, además de constatar que la altura de esta alegoría sagrada de 2 metros de alto se ajusta al espacio aéreo de Las Meninas, lo que prueba, que más que un simple elemento simbólico, representa, sin embargo, el fundamento de una compleja exploración de principios matemáticos y artísticos.
En definitiva, la proporción áurea desempeña, pues, un papel esencial en el equilibrio de la estructura del Árbol de la Vida, y sugiere un profundo estudio de elementos combinados de Matemáticas, Geometría, Arte, Arquitectura y Kabala.
La inspiración
Retomemos el Sefer Yetzirah, cuya trama está inspirada en los tres elementos primarios, fuego,
agua y luz, אש ,מים ,אור, en donde la palabra luz, אור, se transforma en el
vocablo aire, אויר, agregando una letra yod, י, es decir, un aire cuyas cuatro
letras permutadas revelan la mirada prístina, וירא, del espíritu creador.
|
Y vio Dios que la luz era buena; y Dios apartó a la luz de las tinieblas.
וירא אלהים את האור כי טוב ויבדל אלהים בין האור ובין החשׁך׃
Génesis 1:4 |
|
FUEGO |
AGUA |
AIRE |
LUZ |
|
אש |
מים |
אויר |
אור |
| 300 + 1 | 40 + 10 + 40 | 200 + 10 + 6 + 1 | 200 + 6 + 1 |
Y será en el Renacimiento cuando se dé a conocer este manuscrito de tradición oral gracias a los comentarios de Joseph Gikatilla, 1248-1325, que fueron transcritos por Paulus Ricius, del hebreo al latín, en su libro Portæ Lucis. Augsburgo, 1516.
Del Sefer Yetzirah existen distintos comentarios e ediciones impresas:
Paulus Ricius. Portæ Lucis - Augsburgo. 1516
Ioannis Revchlin. De Arte Cabalistica - Hagenau. 1517
Guillaume Postel. Abraham Patriarchœ Liber Iezirah. París. 1552.
Sefer Yetzirah - Mantua. 1562
Johann Pistorius - Basilea. 1587
Joanne Stephano Rittangelio - Ámsterdam. 1642
Athanasius Kircher - Roma. 1652
Pero, eso sí, todos acabaron en el Índice de libros prohibidos, al menos, desde mediados del siglo XVIII.
|
Index librorum prohibitorum Sanctissimi Domini Nostri Benedicti XIV Pontificis Maximi jussu. Recognitus atque editus. Romæ. 1758. |
|
|
Lista de libros prohibidos por orden del Santísimo Señor Benedicto XIV Pontífice Máximo. Revisado y publicado. Roma. 1758. |
|
ספר יצירה |
|
|
|
Liber Formationis |
|
|
|
Libro de la Formación |
|
|
El Sefer Yetzirah es el primer tratado cabalístico que menciona las esferas del Árbol de la Vida, y, como libro de enseñanza, aborda el estudio del proceso de la creación mediante la combinación de las 22 letras hebreas; 22 letras que se comparan con los ladrillos que dispuso el Arquitecto Divino para la creación del mundo.
|
|
|
|
Pondremos de manifiesto, pues, la importancia en la tradición cabalística del valor y significado de ciertas palabras en base a los números pitagóricos por excelencia; 3, 4 y 5, más sus múltiplos y fracciones, que son, en definitiva, los mismos números que establecen el sistema de medidas castellano que utilizamos en la medición geométrica de este óleo.
En la Kabala, el número y su cantidad tienen además el propósito de explicar la importancia manifiesta de una palabra a través de la Gematría, que, en el ejemplo que analizamos, se extrae del nombre de Salomón, שלמה:
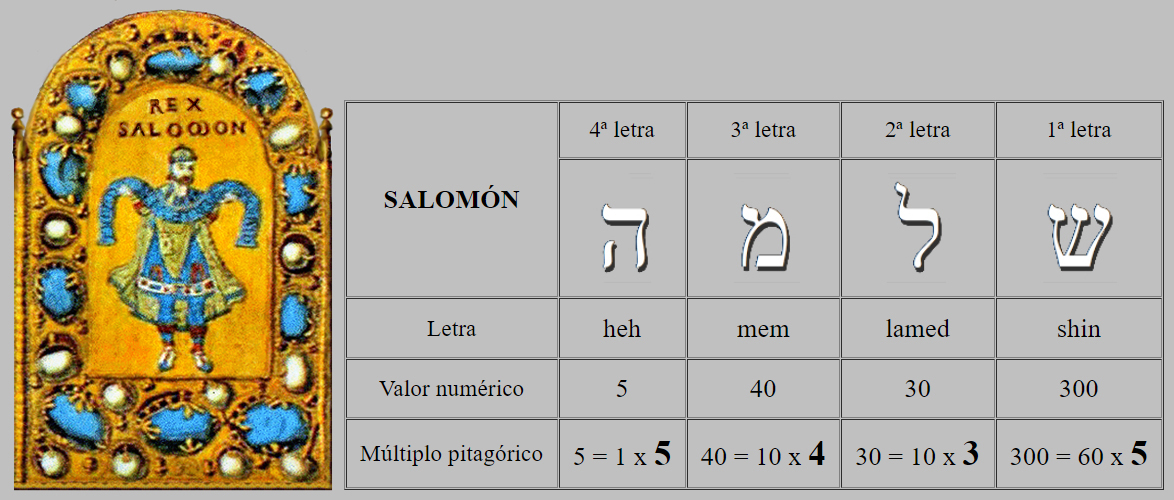 |
|
|
Desde la más remota antigüedad al Árbol de la Vida se le ha identificado con el Árbol del Conocimiento del jardín del Edén, en la creencia de representar los frutos del conocimiento secreto, que la literatura esotérica llama de los misterios.
Y por fortuna, el velo impuesto al símbolo sagrado ya se ha esfumado, revelando, pues, la evidencia de una fe que debería haber permanecido oculta, y que ahora, haciendo justicia, recuperaremos de la Geometría del escenario de esta pintura la aplicación de la Kabala, lo que supone abrir un diálogo con la Sabiduría de las diez esferas del Árbol Sagrado de la Vida.
Estas esferas que descubrimos trazadas en el espacio aéreo de Las Meninas se denominan, pues, los diez Sefirot del Árbol de la Vida, y, como principios sagrados, sus diez atributos poseen cualidades tan especiales que en ellos se descubre un asomo de la esencia divina.
|
Sefira |
Significado |
Castellano |
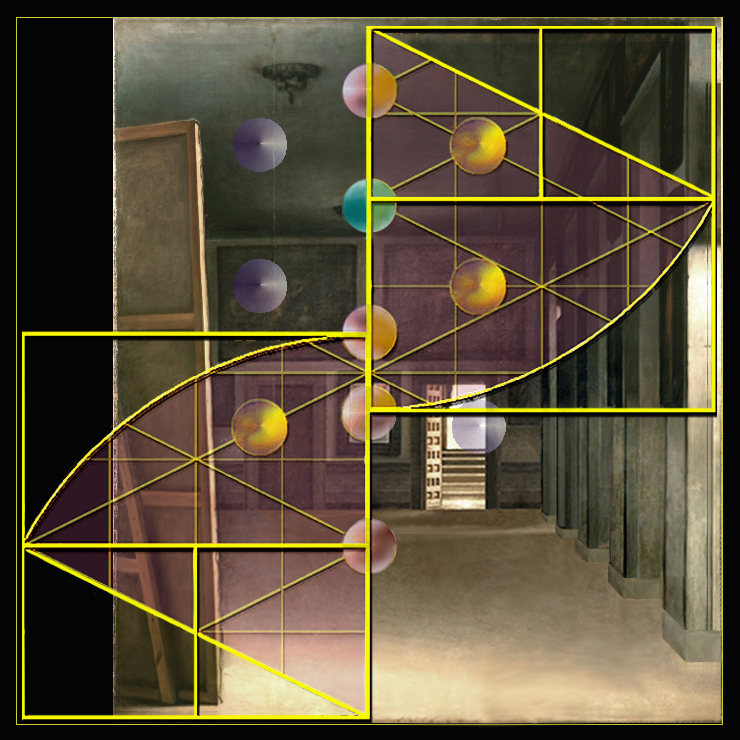 |
|||
|
I |
Kether |
Corona |
רוח אלהים חיים |
El Aliento del Dios Vivo | ||
|
II |
Chokmah |
Sabiduría |
רוח מרוח |
Aliento del Aliento | ||
|
III |
Binah |
Inteligencia |
מים מרוח |
Agua del Aliento | ||
|
Dahat |
Conocimiento |
בלימה |
Nada | |||
|
IV |
Chesed |
Clemencia |
אש ממים |
Fuego del Agua | ||
|
V |
Geburah |
Fortaleza |
רום |
Arriba | ||
|
VI |
Tiferet |
Belleza |
ותחת |
Abajo | ||
|
VII |
Netzach |
Victoria |
דרום |
Sur | ||
|
VIII |
Hod |
Honor |
צפון |
Norte | ||
|
IX |
Yesod |
Fundamento |
מזרח |
Este | ||
|
X |
Malkhut |
Reino |
ומערב |
Oeste | ||
|
עץ חיים
EL ÁRBOL DE LA VIDA |
Es muy revelador que al final del primer capítulo del Sefer Yetzirah se atribuye el origen del universo a los diez Sefirot, donde se explica cómo el Aliento del Dios Vivo se propaga a partir de la Sefira nº 1, Kether, la Corona, la cual establece en el mundo el espíritu, la voz y la palabra, más el centro de las seis direcciones del espacio.
Simultáneamente, como ya ha sido expuesto, el tiento, que el pintor sujeta en su mano izquierda dirigido hacia el techo, establece contacto con la coordenada del punto R: [0, 62], centro de la Sefira nº 1, Kether, כתר, cuyas letras suman 620.
|
|
El paralelismo entre este valor y la ordenada de la coordenada R refuerza, pues, la idea de que Velázquez codificó un simbolismo teológico preciso, desafiando la estricta censura de la ortodoxia de su tiempo.
De modo que en el techo de Las Meninas, la coordenada R marca el punto cero de la contracción de la luz prístina, que como centro de la Sefira nº 1 evoca, además, uno de los nombres divinos más distinguidos de la Torah:
La respuesta de Dios a Moisés cuando le pregunta su nombre.
El nombre divino de esta Sefira se halla en Éxodo 3:14.
Y respondió Dios a Moisés:
YO SOY EL QUE SOY
Eheieh Asher Eheieh
|
|
|
ה |
|
י |
|
ה |
|
א |
|
ר |
|
ש |
|
א |
|
ה |
|
י |
|
ה |
|
א |
|
|
|
5 |
+ |
10 |
+ |
5 |
+ |
1 |
+ |
200 |
+ |
300 |
+ |
1 |
+ |
5 |
+ |
10 |
+ |
5 |
+ |
1 |
= |
543 |
En la tradición cabalística la Gematría del nombre de Moisés, משה, es de 345, una cifra que resulta ser la inversa a 543 de la revelación del nombre de Dios a Moisés en la Zarza Ardiente, una conversación que aquí revela el carácter mítico de la Kabala, y hace posible que la obra respire su propia idea, logrando que el tiempo, el principal enemigo de los mortales, se rinda ante la eternidad de los arquetipos.
|
|
|
|
|
ה |
|
ש |
|
מ |
|
|
|
5 |
+ |
300 |
+ |
40 |
= |
345 |
|
|
Del elaborado peinado de la menina Isabel de Velasco emerge, pues, un inadvertido anciano de fisonomía bíblica, de tez morena y barba canosa, cuya oreja coincide con la de la joven, mientras que su mirada, en un estado entre la súplica y el trance, se dirige hacia la luz que entra por la ventana de la derecha.
Estos toques, de pinceladas blancas y oscuras, son un ejercicio de virtuosismo técnico que apelan directamente al alma del observador, y más allá de aportar textura al cabello, funcionan, pues, como elementos caligráficos hebraicos de carácter esotérico.
Conocemos, pues, a ciencia cierta la identidad de este personaje masculino gracias a los antiguos cabalistas, que situaron en las esferas del Árbol de la Vida a los patriarcas bíblicos según su naturaleza, de manera que Moisés, autor de la Torah y líder indiscutible de la Kabala, quedó representado al pie de la columna derecha en la Sefira nº 7, Netzach, la Victoria, la Eternidad...
Pero, aún hay más, las tres letras consonantes del nombre de la Sefira nº 1 Kether suman, pues, 620; que vienen a ser el número de preceptos que Dios ordenó al pueblo de Israel, y que corresponde, además, a la misma cantidad de letras que componen los 14 versículos de los Diez Mandamientos del capítulo 20 del Éxodo; desde el versículo 3 al 17 inclusive.
Moisés recibió, pues, las Tablas de la Ley en el monte Sinaí un año después de la revelación del nombre de Dios en la Zarza Ardiente.
Pictóricamente, el enganche para lámpara, que denominamos Lámpara Kether, se halla en contacto directo con la esencia de la luz de los pigmentos en la paleta del pintor, cuyo anclaje en el techo de la Habitación del Príncipe es, en definitiva, la evidencia de una profunda intención teológica, que ahora, desatado el nudo gordiano que escondía sus dos cabos, revela el origen de la inspiración que el pintor español mantuvo oculta bajo el barniz de la ortodoxia.
|
|
|
|
Antes de avanzar habría que hacer una aclaración sobre la ubicación de la Lámpara Kether, ya que no se trata de la Sefira nº 1 en sí misma, sino de la carga simbólica que la representa en el plano visual del lienzo, pero determinando en Las Meninas el lugar donde el pensamiento de Dios se hace compromiso.
Al estar suspendida sobre la paleta del pintor, actúa como el anclaje de la voluntad divina, y en cuya marca queda establecido el momento exacto que la luz desciende hacia los pigmentos de la paleta, vinculando, pues, el Creador con la creación artística del pincel de Diego Velázquez.
|
|
|
|
Esta relación vertical recupera la función de Kether, que, como Sefira nº 1, está en íntima relación con la esencia de la luz de los pigmentos de colores, no obstante, esta conexión es la línea divisoria entre el espacio privado del artista y el resto de los retratados, y, aunque el pintor se autorretrata equipado con las herramientas de su oficio, al mismo tiempo, esconde el propósito de su arte en un gran lienzo que da la espalda al espectador a la izquierda de la escena.
|
|
|
|
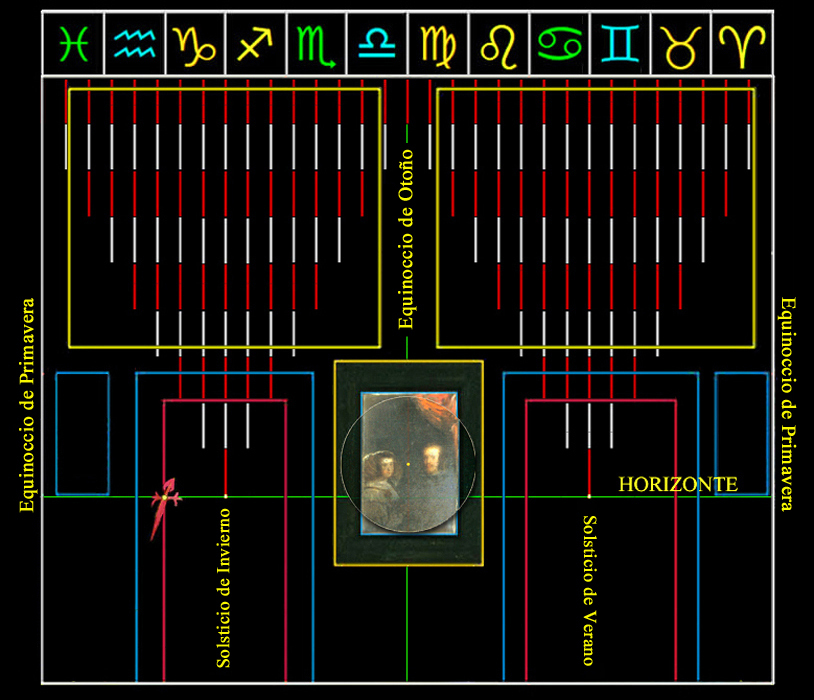
Deberíamos, por tanto, tener bien presente la relación vertical de la lámpara Kether y la paleta de colores, cuyos pigmentos mezclados con aceite representan, pues, la esencia de la luz, y cuya marca temporal se custodia en el Calendario perpetuo de Las Meninas.
|
 |
|
|
El Calendario perpetuo de Las Meninas sugiere que esta obra de arte es una estructura que contiene todos los tiempos del Reino, validados por la rotación de los cielos y el cómputo de las festividades sagradas; tanto hebreas como católicas.
En definitiva, que, adentrándose en el futuro, el origen de la luz divina en la Sefira nº 1, Kether, la Corona, es, además, la generadora de la fuente aritmética que sustenta el sistema de medidas de este lienzo, ya que 20,666666... milímetros equivalen a LA UNIDAD.
Veamos, el valor 62, en la ordenada de la Sefira Kether, está ligado, pues, al tamaño conceptual de LA UNIDAD que utilizamos; 62/3 = 20,666666..., y establece un puente inquebrantable entre el Creador, el Árbol de la Vida y Las Meninas.
Aunque aún es más relevante que 20,666666... equivalga a dos tercios del tamaño de 31 unidades del diámetro de la circunferencia en la demostración del valor de Pi por Arquímedes, (287 a. C. - 212 a. C.).
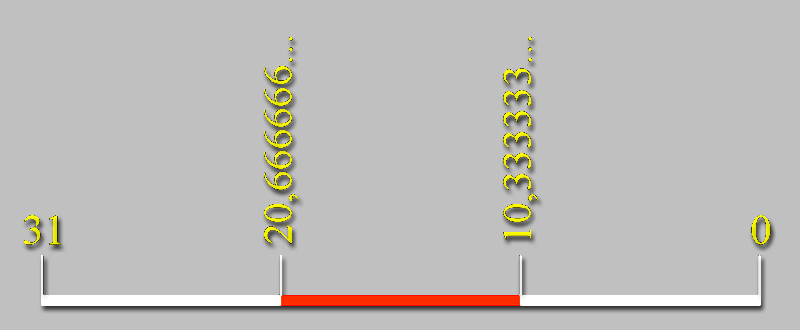 |
31 ÷ 3 = 10,333333... y 10,333333... × 2 = 20,666666...
El Pi de Arquímedes:
π ≈ 198/63 = 22/7
|
El perímetro de la circunferencia vale 97 y 3/7 ≈ 97,428571...
Y el diámetro vale 31
Entonces Pi ≈ 97,428571... / 31 ≈ 3,142857... ≈ 3 y 1/7 = 22/7 |
 |
Esto indica que la cifra que define el tamaño de LA UNIDAD de 20,666666... mm. es la misma cifra que define un tercio de la partición sagrada de la altura de 62 unidades de la Sefira Kether, que, como punto de conexión directo con lo Infinito, es el Punto Primordial que se mide a sí mismo.
Para interpretar esta cuestión, primero habría que entrar en el corazón del sistema métrico de LA UNIDAD, y descubrir que, en el espacio aéreo de esta pintura, 20,666666... mm. es la única cantidad geométrica que permite manifestarse físicamente al Árbol de la Vida.
La Sefira nº 1, Kether, en un sólo punto genera cinco distintas antologías:
Gematría: Las letras del nombre de la Sefira nº 1, Kether, כתר, suman 620.
Bíblica: Los diez Mandamientos se componen de 620 letras. Éxodo 20, desde el versículo 3 al 17 inclusive.
Kabala: La ordenada 62 de la Sefira nº 1, Kether, que al dividirse en tres partes genera la constante 62 / 3 = 20,666666...
Geometría: 20,666666... equivale a dos tercios del diámetro de valor 31 en la demostración de Pi por Arquímedes.
Aritmética: Y aunque en el siglo XVII no existía el metro, 8/9 de pulgada castellana equivale, pues, a 62 / 3 = 20,666666... milímetros.
Y sería justo ya decir que la ordenada de Kether equivale al doble del diámetro del círculo de la demostración de Pi por Arquímedes, de modo, que se demuestra que Velázquez ancló su obra en una fracción específica de la medida oficial del Reino, para que su tamaño se igualara con una constante universal derivada de la luz infinita del nombre de Dios.
Es notable, que la presencia de la luz divina, en su estado más puro y matemático, dote al espacio aéreo de esta pintura un profundo significado.
|
|
|
Tsimtsum
Reducción, restricción, hacer algo pequeño y limitado en tamaño, cantidad, rango, potencia... |
Diego Velázquez, al fijar en el techo el punto cero de la contracción de la luz en la coordenada R, [0, 62], acomete la restricción divina del Tsimtsum con el propósito de generar el espacio vacío donde la creación es posible, lo que indica que en este punto R se produce el suficiente vacío para que la luz descienda y se transforme en una medida lineal estable para construir lo representado en la Habitación del Príncipe.
Esta idea queda expuesta en el libro de Athanasius Kircher: Oedipus Aegyptiacus, editado en Roma en 1652, una obra singular y contemporánea a Las Meninas donde se explica, con detalle, la zona superior del Árbol Sefirótico.
|
|
|
El Árbol Sagrado de la Vida |
El Tsimtsum no es sólo un concepto teológico, sino que es antecesor a la rejilla de 152 unidades, que es la estructura geométrica donde se asientan las 10 esferas + 1 del Árbol de la Vida.
Hemos accedido, pues, al territorio donde la Geometría se convierte en confesión de la fe más íntima de Diego Velázquez, la cual se aleja del dogma establecido para abrazar una espiritualidad más antigua y universal.
Y dado que esta interpretación de Las Meninas no es un hecho todavía consensuado, es imperativo protegerla de la vehemencia que pudiera generar, lo que sugiere una resistencia visceral que va más allá del mero desacuerdo académico:
Los dogmas pueden debatirse,
las pinceladas pueden interpretarse,
pero las proporciones exactas son la Geometría que habla.
LA UNIDAD interpreta, pues, un encuentro indescriptible en el techo de esta pintura donde la luz infinita de Kether disuelve el dato numérico.
La Geometría es, al final, la forma más alta de la contemplación, donde el alma reconoce que no es una herramienta para dominar la materia, sino el espejo más limpio para contemplar lo invisible.
 |
|
Hans Vredeman de Vries. 1604 |
En este contexto, se podría considerar la posibilidad de que este hallazgo provoque una mala lectura adicional dada la naturaleza del origen de la tradición oral hebrea, que se valió de la boca y del oído para conservar fuera de la vista a la Kabala, pero, en este óleo, una vez que Velázquez rompe el secreto de la transmisión oral para fijarlo en la materia, el ojo se convierte, sin menoscabo alguno, en el testigo fehaciente de una fe que, por razones históricas, debía permanecer de forma indeleble en la materia del lienzo.
Y por esta razón, la precisión de este hallazgo es el nexo que une la ciencia con el misterio de la fe, en un mundo actual reticente que se empeña en mantenerlos separados.
|
|
|
|
No obstante, este enfoque sugiere que la estructura geométrica de este lienzo no sólo refleja el alto conocimiento del pintor Diego Velázquez en las matemáticas de la perspectiva, sino también una profunda comprensión de la enseñanza cabalística, la cual se halla integrada como recurso iconográfico.
Aparentemente, pues, una explicación distante a las habituales de esta obra maestra, sin embargo, este era su legado.
Y este es el punto de inflexión, entre la Kabala Práctica entendida como Magia, y la Magia que realiza cosas sorprendentes; en ambos casos se usa una fórmula según el ritual acostumbrado, aunque la Magia, a diferencia de la religión, que postula la humildad y pide por medio de plegarias, se ve a sí misma como arte o ciencia.
En el nivel más básico de medición de la superficie del lienzo sólo es necesario una simple regla, ya que todo el cálculo se halla a la vista, engarzado a una rejilla de trabajo dividida en intervalos exactos de tres unidades, por lo que no hay peligro de perderse en la búsqueda de las coordenadas del Árbol de la Vida, de manera que operar geométricamente en Las Meninas se hace sencillo.
|
|
|
|
Una Geometría legendaria
Entendida la
complejidad del escenario de esta pintura, la tradición
cabalística afirma que la emanación divina de los diez Sefirot
se manifiesta en el mundo físico a través de
la Sefira nº 1, Kether, la Corona del Árbol Sagrado de la Vida, y, si bien, hablamos de un legado de la milenaria andadura de la Kabala que el óleo de
Las Meninas salvaguardó, también confirmamos que el
reencuentro fortuito con su modelo original se produjo en
un grabado de un libro editado en 1642 en Ámsterdam.
El Sefer Yetzirah comentado en hebreo por Yosef ben Shalom Ashkenazi, y traducido al latín por Joanne Stephano Rittangelio.
 |
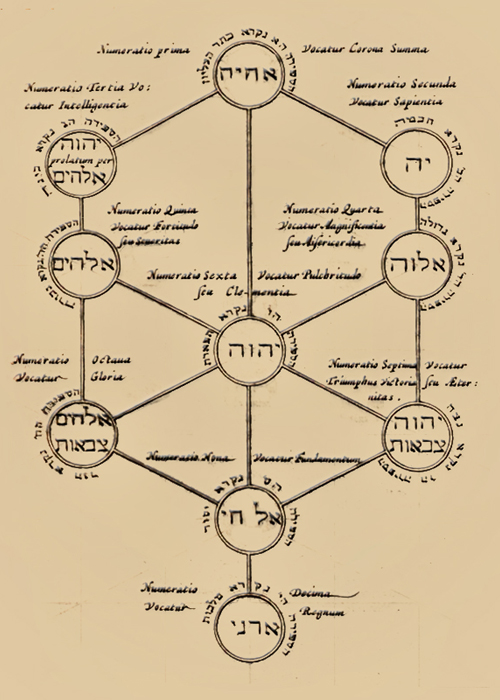 |
|
|
Cada letra, idea, palabra o imagen de este texto fue analizada, en profundidad, por el pintor español Diego Velázquez.
El libro de Joanne Stephano Rittangelio, en pleno siglo XVII, no sólo constituye el detonante cabalístico de Las Meninas, sino que se le podría considerar el motivo de la resuelta decisión velazqueña de plasmar la sublimación del Arte de la Magia Operativa con el beneplácito de la Kabala judía.
En definitiva, una estructura legendaria que es el santo y seña de Las Meninas, y que, básicamente, nos remite a la misma idea que se conserva en el despliegue geométrico de las trece roelas azules en el escudo de Armas del apellido Velázquez.
 |
Los Velazquez traen por Armas treze Roeles azules en campo de plata, y por orla ocho Aſpas de oro en campo roxo. |
|
Gonzalo Argote de Molina
Sevilla - 1588 |
El origen heráldico de los Roeles según Gonzalo Argote de Molina [9]:
|
De ſu antiguedad eſcrive Barbe Ragnault; tienen ſu principio de el Rey Artur de Inglaterra, que inſtituyó los Cavalleros de la Tabla Redonda, y les dio orden de Cavalleria, Armas y Deviſas. De los quales fueron muy famoſos Genaſio el Fuerte, Mador de la Puerta, y Perſides el Gentil. Al primero dio por Armas treze Roeles roxos en campo de oro. Al ſegundo ſiete Roeles de plata en campo negro. Al vltimo los Roeles azules en campo de plata, como oy los vſan los de Caſtro. |
El escudo de Armas de Velázquez es, por tanto, una divisa incrustada en otra idea dotada de un gran valor simbólico que nunca dejó de acompañar a su propietario.
 |
|
Genaſio el Fuerte |
Mador de la Puerta | Perſides el Gentil |
|
Este que ves entre moriscas lides Con seis azules roeles señalado, Antiguas armas del Gentil Persides, En tiempo del Rey Artus celebrado; |
| EL
BERNARDO, POEMA HEROYCO Bernardo de Balbuena |
Don Bernardo de Balbuena, Obispo de la isla de San Juan de Puerto Rico, en su libro titulado: Bernardo del Carpio, que fue impreso en Madrid en el año mil seiscientos veinticuatro, no se olvidaba de mencionar a Gentil Persides, el ancestro del pintor sevillano.
Para establecer la verdadera idiosincrasia de Diego Velázquez habría que sopesar, pues, que no sólo encontramos en su comportamiento artístico ideas morales muy distintas a sus contemporáneos, a lo que se sumaría, por su condición privilegiada de pintor del rey, el constante estímulo de un entorno sin rivales en el proceso de su redención personal.
Compararemos, pues, el Árbol de la Vida del óleo de Las Meninas respecto al grabado del Árbol de Joanne Stephano Rittangelio:
La escala: 986,7975 veces a 3,
la similitud geométrica,
la concordancia de las medidas en unidades
y la simbología.
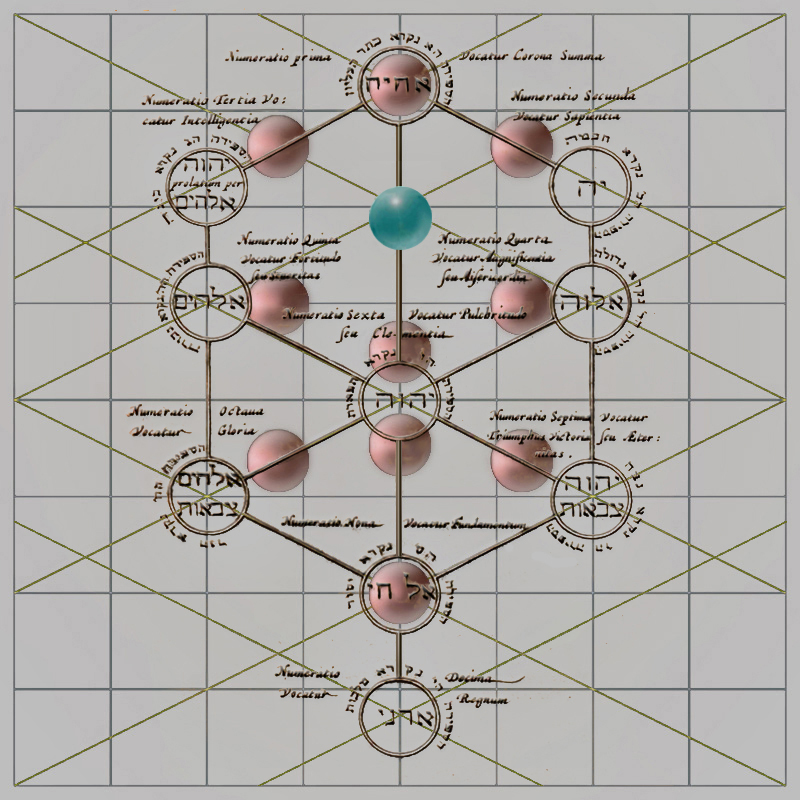 |
Numeración |
Hebreo |
Velázquez |
Rittangelio |
|
I |
Kether |
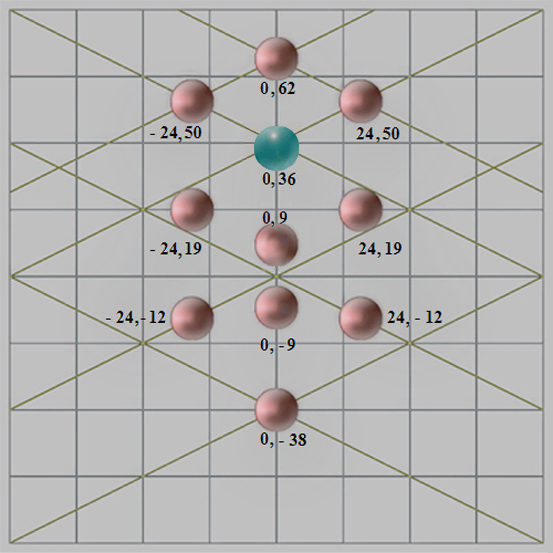
0, 62 |
0, 62 | |
|
II |
Chokmah |
24, 50 |
38, 43 | |
|
III |
Binah |
- 24, 50 |
- 38, 43 | |
|
Dahat |
0, 36 |
|||
|
IV |
Chesed |
24, 19 |
38, 19 | |
|
V |
Geburah |
- 24, 19 |
- 38, 19 | |
|
VI |
Tipheret |
0, 9 |
0, 0 | |
|
VII |
Netzach |
24, - 12 |
38, - 19 | |
|
VIII |
Hod |
- 24, - 12 |
- 38, - 19 | |
|
IX |
Yesod |
0, - 9 |
0, - 38 | |
|
X |
Malkut |
0, - 38 |
0, - 62 |
|
El Árbol de Joanne
Stephano Rittangelio. Ámsterdam. 1642 El Árbol de Diego Velázquez. Madrid. 1656 |
Analizamos, pues, dos diseños originales de magnitudes desiguales en un mismo sistema de coordenadas, en donde, no sólo se comprueba que el 100% de las posiciones de las esferas están planificadas adecuadamente, sino que en la determinación del pintor Diego Velázquez se descubre la causa de una sólida razón que le obligaba a guardar las apariencias ante todo tipo de sospecha.
La prueba geométrica del método estadístico de Monte Carlo certifica; que la probabilidad de que las coincidencias geométricas analizadas se deban al azar son extremadamente bajas, lo que confirma un patrón consistente de traslación lateral y vertical en el desplazamiento de las Sefirot [10].
Esto apoya la hipótesis de que existe una relación no aleatoria entre estas dos configuraciones:
ya sea una transformación geométrica deliberada por parte de Velázquez
o una conveniencia compartida del plano de los diez Sefirot.
En resumen, el método estadístico de Monte Carlo respalda de manera sólida que la disposición de los Sefirot en Las Meninas es el resultado de una decisión compositiva deliberada y planificada, y no un accidente, por lo que el pintor, al codificar en su obra maestra las profundas raíces de la tradición espiritual occidental de la Kabala, se merece, pues, el sello de validación científica de la intencionalidad.
Estos resultados apoyan, pues, que la coherencia entre los dos diagramas es la prueba que permite sostener que Velázquez no inventó nada nuevo; ya que utilizó, mediante una transformación geométrica, la misma disposición de los Sefirot en el Árbol de Las Meninas que en el modelo precursor del Árbol de Joanne Stephano Rittangelio.
Hagamos, pues, la comparación de tamaños entre estos dos diseños geométricos:
El Árbol Sagrado de la Vida de Las Meninas.
y el diagrama del Árbol de Joanne Stephano Rittangelio,
| Autor | centímetros | centímetros cuadrados | proporción | ||||
| Velázquez |
314,1333... |
x |
314,1333... |
= | 98679,75 | 986,7975 veces a 3 | |
| Rittangelio | 20 | x | 15 | = | 300 | ||
Es indudable que la Geometría de este pequeño grabado holandés de 20 x 15 centímetros, que magistralmente Velázquez adaptó a escala en su obra maestra, genere nuevas respuestas, ya que, ilustrando a Las Meninas con esta novedosa característica, no sólo estaríamos descifrando un asunto cuya envergadura supera la sorpresa que provoca, sino que, además, proporcionaría un contexto histórico, y legitimaría, pues, la aplicación de la simbología cabalística en la interpretación de esta obra maestra.
El resultado de esta comparación con Rittangelio no sólo avala la gestación de este tipo de estructura geométrica en Las Meninas, sino que demuestra, lejos de cualquier arbitrariedad, la similitud con los procedimientos establecidos en el estudio de la Kabala a lo largo de su historia.
Y aunque el diagrama del Árbol de la Vida de Rittangelio fuera publicado 14 años antes de que Velázquez pintara su óleo, el pintor español no sólo tuvo tiempo de tomar prestada la idea de Rittangelio, sino que mantuvo principios métricos idénticos que codificó en Las Meninas, y, ya que ambos compartieron el mismo lenguaje geométrico, utilizaron, pues, el sistema de LA UNIDAD.
 |
|
|
La específica relación, entre el tamaño de la Sefira de Rittangelio y la de Velázquez, es de 4/3; un ratio que demuestra que la estructura general de ambas Geometrías, las posiciones puntuales de los Sefirot y la magnitud de las esferas cabalísticas guardan una proporcionalidad exacta.
El pintor plantea, por tanto, todo un gran desafío de acuerdo con la lectura interior de esta pintura:
La aplicación de la Geometría áurea
y la enseñanza trascendente de Las Meninas.
En definitiva, una piedra preciosa de la Geometría, y su relación con las diez esferas cabalísticas del Árbol Sagrado que coronan la sublime experiencia sensorial de este lienzo:
Un vínculo presente en Las Meninas expresado desde puntos muy concretos.
|
|
|
|
Elementos de la Geometría
La limpieza de Las Meninas en el año 1984 documentó aspectos técnicos que han dado pie a nuevas observaciones [11]; y cierto es que Velázquez, aún pintando con verismo, dejó abierta la posibilidad de sopesar más de una explicación de las distintas fases del proceso de su óleo.
Trabajamos, pues, con la copia de la placa fotográfica de 12 x 18 centímetros que se tomó durante la restauración de Las Meninas en 1984, es decir; se trata de una imagen de gran calidad de 28,9 megas en formato TIF descomprimido de 2917 por 3455 píxeles [12].
En cuanto a esta instantánea, detectamos, pues, que el chasis de la placa fotográfica, de la cámara técnica de gran formato utilizada para la ocasión, no estaba exactamente nivelado respecto al plano horizontal del lienzo de Las Meninas; por lo que esta fotografía, ya digitalizada, la giramos - 0,3 grados en el programa Adobe Photoshop 7.0 para corregir la vertical y horizontal de la composición.
|
|
|
|
Si bien, y debido a que en la sesión fotográfica el óleo de Las Meninas estaba apoyado directamente en una pared, su eje vertical se hallaba inclinado, por lo que constatamos la falta de 1,18 pulgadas en la altura de la foto, es decir; 1,3275 unidades, que representan 0,027435 metros en la imagen escaneada, aunque, afortunadamente, subsanamos este error gracias al programa vectorial Corel Draw.
Sin duda, ha sido la Geometría que desarrollamos la que ha detectado esta inexactitud en la copia fotográfica digitalizada del 0,86... % para la altura y del 0 % para la anchura.
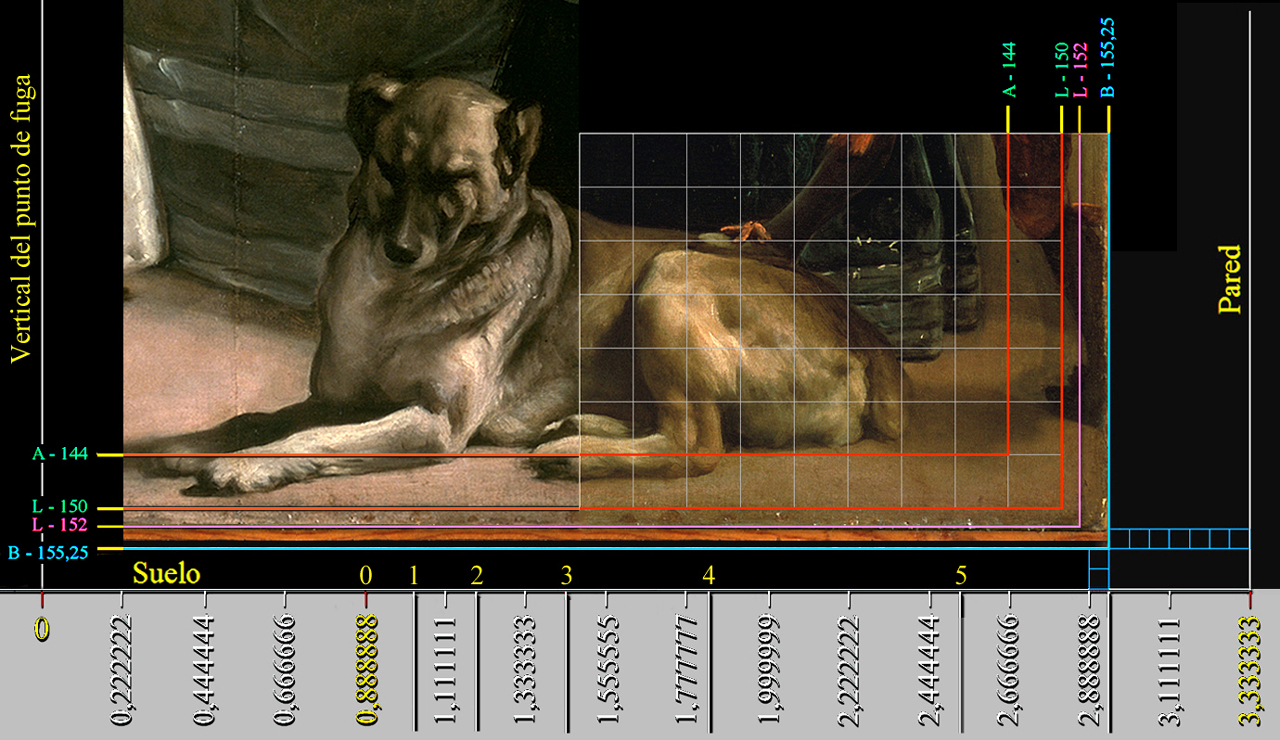 |
|
|
Para evitar errores de medición, fundamentamos, en un mar de conjeturas, todo resultado numérico en reglas de Geometría y en un modelo matemático exacto, que todo el mundo debería conocer.
Tipos de cuadrículas sobre la superficie de Las Meninas:
 |
|
Estas cuatro cuadrículas concéntricas sobre la superficie de Las Meninas están sometidas al mismo sistema de medidas y coordenadas, ya que mantenemos, como centro neurálgico de la estructura que organiza este plano, el punto E situado en la parte superior del Espejo.
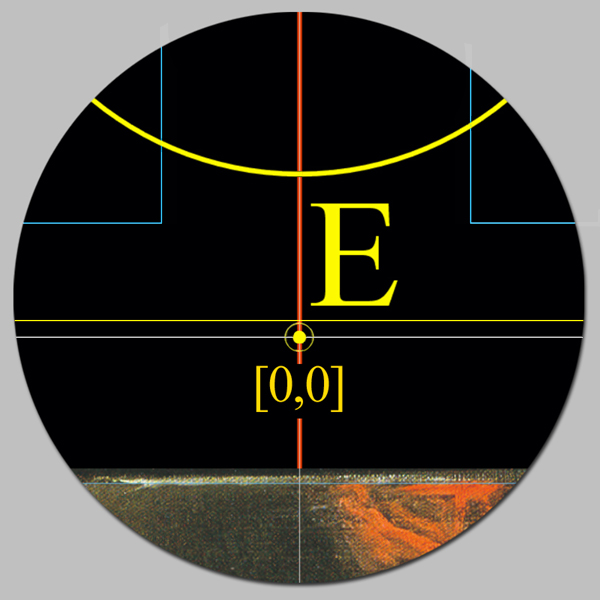 |
[0, 0]
| Modelo | Cuadrículas | Lado en unidades | Lado en pulgadas | Abscisa X | Ordenada Y |
| A - 144 | Línea de acotación | 144 | 128 | 0 | 0 |
| L - 150 | Límite de la rejilla de 150 unidades | 150 | 133 y 1/3 | 0 | 0 |
| L - 152 | Límite de la rejilla de 152 unidades | 152 | 135 y 1/9 | 0 | 0 |
| B - 155,25 | Borde del orillo del lino original | 155,25 | 138 | 0 | 0,375 |
|
Para que la Geometría de Las Meninas sea operativa debe esta anclada en un punto de origen absoluto, y aunque hemos detectado que la cuadricula del Borde del orillo del lino original, tiene una desviación técnica de 0,375 unidades en la ordenada.
Este valor, que equivale a 1/3 de pulgada castellana de 7,75 mm., es el margen de ajuste entre el lino del lienzo y la proyección geométrica, y, sin este tercio de pulgada, las cuadrículas concéntricas de 144, 150 y 152 unidades no alcanzarían la perfecta simetría que permite ubicar los Sefirot en su lugar exacto.
 |
|
El orillo de la tela original en el lateral derecho |
Y señalaríamos, que el orillo es el borde del tejido donde los hilos transversales cambian su dirección, y en el lienzo de Las Meninas queda acotado, por su lateral derecho y superior, por la cuadrícula de trabajo de 155,25 unidades, denominada Borde del orillo del lino original de 138 pulgadas.
La Geometría de Las Meninas fue proyectada, pues, a partir de un cuadrado de 3,141333... metros de lado, y equivalente a 152 unidades, cuyo centro quedó instalado en la parte superior del marco del espejo con los reyes de España reflejados en su interior [13].
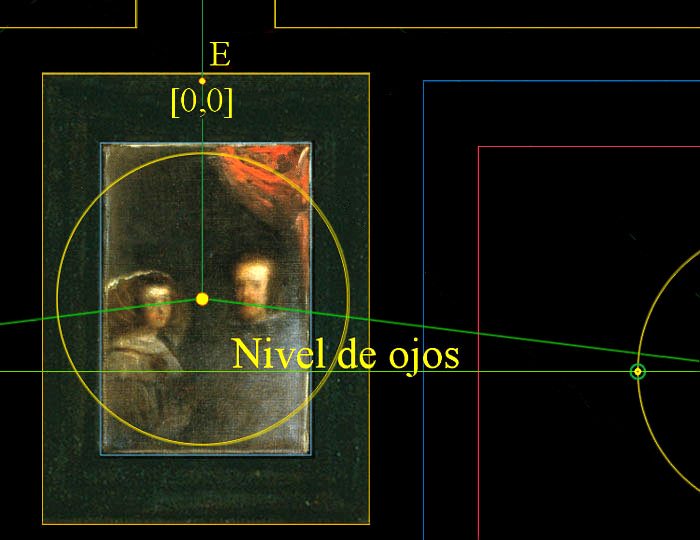 |
 |
|
|
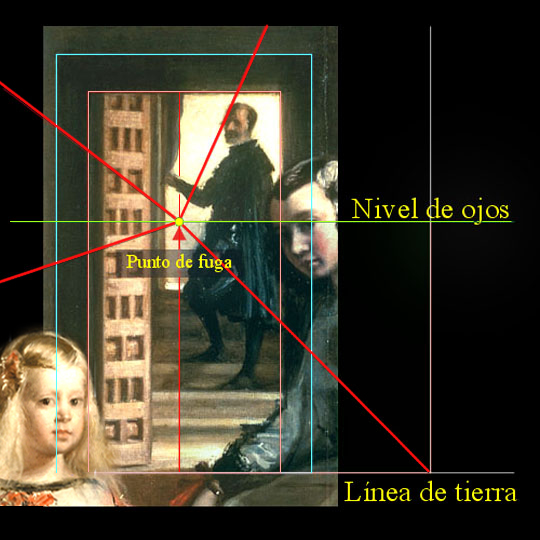
Conjuntamente, Diego Velázquez aplicó su arte para manipular la realidad, proponiendo un complejo análisis de efectos de luz, estableciendo el origen matemático de la perspectiva en el punto de fuga áureo, justo detrás de la puerta semiabierta de veintidós cuarterones, en la refulgente y última pared de la pieza arquitectónica, para que, de forma inmediata, indujera al espectador a un entorno de tres dimensiones [14].
Esta profundidad está acentuada, pues, por los cuarterones oblicuos de la puerta semiabierta, y esta sensación es notable en la pared sur derecha, en donde se alinean las ventanas y los cuadros colgados en la pared, lo que crea un ambiente natural.
Y no hay duda, pues, del efecto de la perspectiva aérea como culminación del esfuerzo del pintor, pero, sorprendentemente, venía acompañada de diez principios sagrados desplegados etéreamente en el aire de Las Meninas, y, de igual número, que los diez círculos que circundan el marco gótico del espejo de la tabla de Van Eyck [15].
Diez círculos que relatan la Pasión y Resurrección de Cristo, y transforman al espejo en un objeto sagrado.
 |
 |
|
National Gallery de Londres - firmado en el año 1434 por Jan Van Eyck |
Se constata, pues, que tanto Jan Van Eyck, como Diego Velázquez 222 años después, centró su composición gracias a un espejo, lo que sugiere un profundo interés por los efectos ópticos de la luz y de la Geometría Sagrada del decágono.
Sabemos que, en el caso del Matrimonio Arnolfini, los diez medallones circulares alrededor del espejo incorporan escenas de la Pasión de Cristo. lo que añade a esta obra una dimensión piadosa, aludiendo, pues, al sacrificio y al sacramento del matrimonio.
En la propuesta de los diez Sefirot alrededor del marco del Espejo de Las Meninas habría que destacar, sin embargo, a los monarcas retratados dentro de la representación física de la Sefira nº 9, Yesod, cuyo Fundamento legitimaría el origen sacro de la monarquía.
 |
|
|
Los diez círculos, que enmarcan al espejo de Las Meninas, revelan, pues, una idea susceptible de ser interpretada bajo la luz de diversas perspectivas; óptica, astrológica, filosófica, esotérica, religiosa, mística o cosmológica.
Sabemos que la Kabala es una tradición mística del judaísmo que busca comprender la naturaleza de Dios y del universo a través de símbolos y alegorías, en la que, por medio de las diez emanaciones divinas denominadas Sefirot, Dios se manifiesta y crea el mundo.
Como cabezas visibles de la Monarquía, la imagen de los reyes de España retratados dentro de la Sefira nº 9, Yesod, el Fundamento, explica, pues, un llamativo mensaje refugiado en la base de la estructura del Árbol de la Vida.
Yesod, la novena Sefira, actúa como un canal que recibe la energía de las Sefirot superiores y la transmite directamente a la Sefira nº 10, Malkhut, el Reino, la décima y última Sefira, que representa la manifestación terrenal del reino divino.
La Sefira nº 10, Malkhut, El Reino, es virtualmente el centro de la materia; o sea, el mundo creado por Dios.
 |
Imagen mágica
Una joven mujer coronada y entronizada.
Adonai Ha Aretz - Señor de la Tierra |
La acción que se desarrolla sobre el óleo captura el instante preciso en que la mano derecha de la Infanta Margarita toma su herencia, simbolizada por la jarrita roja de Tonalá; pieza de barro, que ofrecida, bajo la solemne presencia de los monarcas, por la menina María Agustina Sarmiento encarna, pues, a Malkhut, el Reino, la décima Sefira que actúa como el receptáculo de la luz divina en el mundo material, y que, al ser de barro cocido, evoca humildemente el nombre divino Adonai Ha Aretz, el Señor de la Tierra.
Siguiendo el orden inmutable impuesto por la Kabala, la Infanta Margarita debe primero alcanzar el contacto con Malkhut, y sólo tras establecer este vínculo con la realidad del Reino, podrá aspirar a gobernar imbuida de las propiedades de las demás Sefirot.
Esta iconografía, de naturaleza estrictamente cabalística, descifra la responsabilidad política de la Infanta Margarita, cuya declaración visual proclama su cometido dinástico y su lugar legítimo en el orden del Reino, que en 1656 ya estaba escrito en las estrellas y en el lino de este óleo con una huella que el tiempo no ha podido borrar, lo que convierte a esta pintura en un acta de legitimidad eterna, donde la Geometría se funde con el misterio de la fe.
El carácter divino de la Sefira nº 10, Malkhut, el Reino, se entiende como el receptáculo final donde las energías divinas se materializan, lo que revelaría que Velázquez está manifestando con claridad meridiana la idea de que la potestad de los monarcas no era puramente terrenal, y además explicaría por qué la Infanta Margarita tiene un protagonismo absoluto, no solo retratada como figura central, sino como una heredera consagrada por el derecho divino.
El baluarte
El Espejo de Las Meninas de Diego Velázquez utiliza, pues, una base decagonal, que, como eje central compositivo, fue la misma idea que utilizó Jan Van Eyck, lo que sugiere que ambos artistas compartieron un común interés por las características geométricas del decágono.
Militarmente, la Geometría de la Ciudadela tenía forma de estrella de cinco puntas, siendo cada una de sus puntas un baluarte, de modo, que se podría afirmar que cada una de las cuatro esquinas del marco del Espejo equivale a un baluarte.
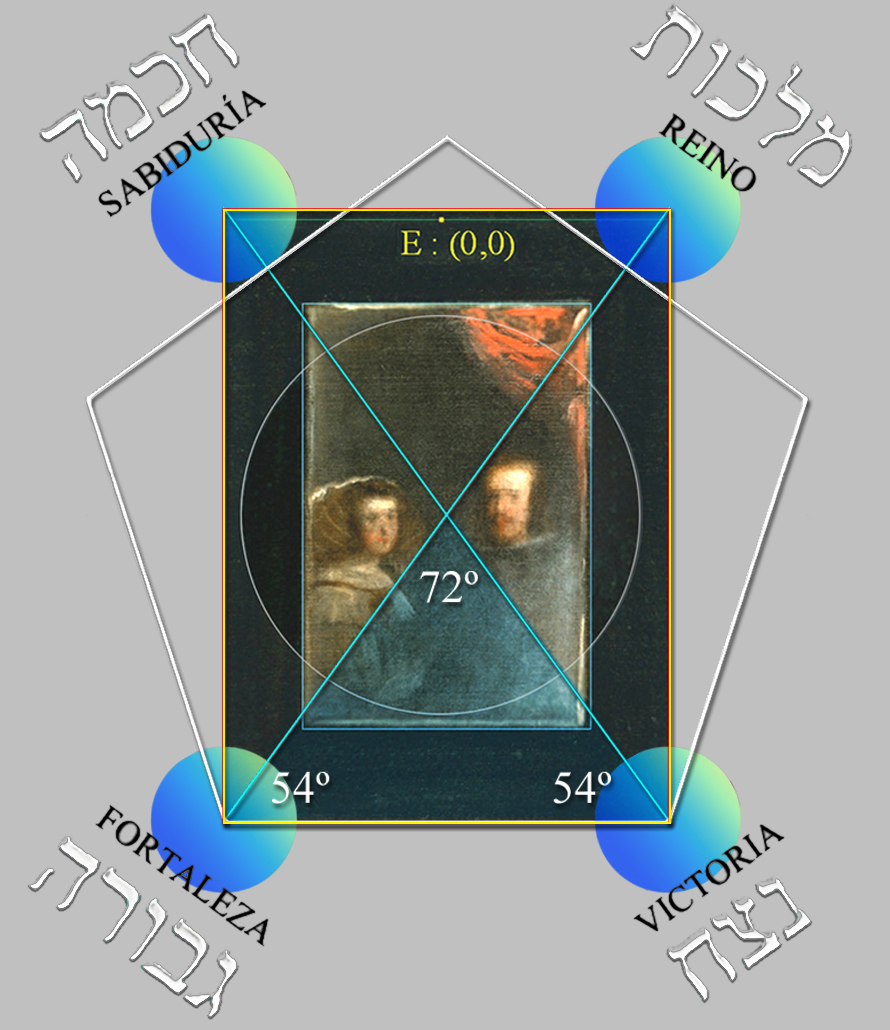 |
|
|
INTERPRETACIÓN
|
מלכות - Malkhut - El Reino - Señor de los Ejércitos
חכמה - Chokmah - La Sabiduría - Suprema
גבורה - Geburah - Fortaleza - Misericordiosa
נצח - Netzach - Victoria - Rey del mundo
|
RESUMIENDO
Los centros de los diez círculos que rodean al espejo de Van Eyck se situaron, pues, en los diez vértices de un decágono regular,
no obstante, Velázquez en Las Meninas estructuró el Espejo a partir de la Geometría de dos pentágonos superpuestos, en los que cuatro de sus vértices determinaron el formato del ancho y alto del marco de madera del Espejo.
|
|
|
Proyecto de fortificación para La Mámora, 1614. Archivo General de Simancas |
En lo referente a arquitectura militar, en la librería de Velázquez, [16], se encontraban varios tratados de fortificación; el de Jacobo Fusti Castriotto, (5 y 6), La Arquitectura militar, (47), de Gabriel Busca, y el Arte militar, (63), de don Carlos Bonieres, un tipo de manual que tienen en común el trazado de ciudadelas pentagonales de plazas recién conquistadas, y diseñadas para controlar a su población para evitar revueltas.
Una ciudadela es una fortificación con forma de estrella de cinco puntas, que optimiza la defensa mediante baluartes en sus ángulos, que, como hemos ya señalado, su Geometría concierne también a la que Velázquez hizo prevalecer en la inspiración pentagonal del Espejo, tanto por su carácter defensivo como protector.
La precisión métrica, que Velázquez utiliza en el lienzo Las Meninas, es consecuencia de su responsabilidad como Aposentador Mayor, ya que tenía bien domeñado el espacio físico del Alcázar por sus intervenciones arquitectónicas en el Salón de Espejos; cuya reforma fue el preámbulo técnico que le permitió proyectar sobre su lienzo en 1656 una estructura tan sólida como un muro de piedra.
En el siguiente paso compararemos la altura del Marco del Espejo, que mide 16,533333.. pulgadas, con el tamaño de la Apotema de un pentágono de 12 pulgadas de lado.
|
|
CÁLCULO DE LA APOTEMA:
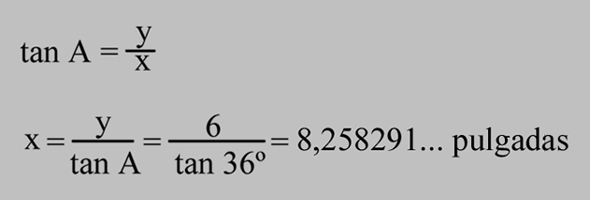
La fórmula de la tangente de un ángulo agudo, A, en un triángulo rectángulo es igual al cateto opuesto al ángulo analizado, y, dividido por el cateto contiguo, x, y, despejando, tenemos que el cateto contiguo, x, que trata del tamaño de la Apotema que buscamos, es igual al cateto adyacente, y, de 6 pulgadas, dividido por la tangente de 36º.
La tangente de 36º es aproximadamente igual a 0,726542...
y a la altura del Marco del Espejo le corresponde, pues, dos Apotemas, es decir; 8,258291... × 2 = 16,516582... pulgadas.
aunque la altura del formato del Espejo es de 16,533333... pulgadas.
Luego, 16,533333... pulgadas, de la altura del formato del Espejo, menos la medida de 16,516582... pulgadas es igual a 0,016751... pulgadas, es decir; una diferencia de 0,389460... milímetros.
En definitiva, el Pie Real de 12 pulgadas es el legítimo patrón de medidas castellano, y ejerce el control absoluto sobre las medidas de este lienzo, y, como se puede comprobar, quedó puntualmente plasmado, sin duda, en la misma anchura del Marco del Espejo.
|
|
|
|
| Marco del Espejo | Pulgadas | Metros | Unidades | Unidades por pulgada | Pulgadas reales | |||
| Altura | 16 y 8/15 | 0,3844 | 18,6 | ÷ | 0,3 | = | 62 | |
| Anchura | 12 | 0,279 | 13,5 | ÷ | 0,3 | = | 45 |
|
|
Este procedimiento tan exacto da entrada, pues, a un territorio desconocido, donde Velázquez, en el centro del Espejo, dispuso a la Sefira nº 9, Yesod, el Fundamento, con la finalidad de que el rey Felipe IV y la reina Mariana de Austria refrendaran, a partir de entonces, una Alianza divina.
 |
 |
|
|
|
Dejemos, pues, que un especialista en la materia, Z´ev Ben Shimon Halevi, nos explique que representa Yesod en el Árbol Sagrado [17]:
|
En primer lugar, es generativo; desde este punto, como veremos, se manifiestan otros Árboles. En segundo lugar es reflexivo; aquí, directamente bajo Tiferet, se puede percibir una imagen de la imagen, y el Árbol se ve a sí mismo; Yesod es el espejo dentro del Espejo.
Estas dos funciones complementarias significan que su constitución, o Fundamento, debe ser clara y sólida; de ahí el significado interno de pureza sexual asociado a esta Sefirah. |
Pocas lecturas aclaratorias sobre Kabala se ha mostrado tan abiertamente atemporal, si se añadiera a esta definición una palabra de más quizá estaríamos hablando de otra cosa, pero no, hablamos del mismo arquetipo.
No obstante, Velázquez, en la variedad de su estilo naturalista, en el Espejo pinta la presencia de los monarcas con doble apariencia; la reflejada en el Espejo, y su ausencia ante el lienzo como personas físicas.
De manera, que los monarcas, al no estar concretamente ante el lienzo, se evitan la degradación de la materia; la vejez, la enfermedad, la muerte..., y, por este motivo, su retrato en el Espejo se convierte en un arquetipo eterno.
La unificación
Damos a conocer, pues, un patrón geométrico de unidades longitudinales que pone de acuerdo al Pie Real Castellano del rey Felipe II, al Metro francés de Napoleón Bonaparte, y a la pulgada anglosajona de Eduardo II de Inglaterra.
|
Magnitud |
Año |
Divisiones |
Milímetros |
Pulgadas castellanas | Unidades |
|
Pie Real Castellano del rey Felipe II |
1568 |
12/12 |
279 |
12 | 13,5 |
|
Shaku japonés |
1650 | 10/10 | 302,25 | 13 | 14,625 |
|
Metro francés de Napoleón Bonaparte |
1800 |
1000/1000 |
1000 |
4000/(3×31) | 1500/31 |
| LA UNIDAD | 2000 | 9/9 | 20,666666... | 8/9 | 1 |
|
Pulgada estándar inglesa |
1959 | 8/8 | 25,4 | 508/(5×3×31) | 381/(31×10) |
|
Pulgada exacta inglesa |
2025 | 8/8 | 1600/63 | 6400/(63×3×31) | 800/(21×31) |
Este modelo comparativo de medidas no sólo permite convertir magnitudes con precisión, sino que ofrece una base geométrica para el análisis de obras como Las Meninas, donde las proporciones del lienzo, los objetos y los personajes pueden ser interpretados en términos de esta unidad racional, además de reconciliar arte, ciencia y tradición bajo un mismo sistema de medida.
La pulgada inglesa estándar de 1600,2/63 milímetros = 25,4 mm., oficialmente adoptada en Julio de 1959 mediante un acuerdo entre los laboratorios de metrología de EE.UU., Canadá, Reino Unido, Australia y Sudáfrica, prevaleció gracias al criterio del tamaño conversor de Carl Edvard Johansson, ya que llevaba utilizándose desde hacía 47 años con absoluta regularidad, y, no obstante, es equivalente a la Pulgada exacta inglesa de 1600/63 milímetros.
Como toda medida histórica, la pulgada castellana es una medida antropométrica, es decir; una unidad de longitud equivalente al tamaño de la falange distal del dedo pulgar, mientras que LA UNIDAD es una constante universal de otra índole que ha convivido, a través de la historia, con sistemas de medidas como el castellano, que es precisamente el sistema donde se revela la relación matemática exacta; 1:1,125 ó 8:9, que conecta con LA UNIDAD FUNDAMENTAL.
Es concluyente que LA UNIDAD, a diferencia del pie castellano, el metro francés o la pulgada inglesa, establecidos por conveniencias políticas en momentos históricos puntuales, es, pues, una constante matemática inherente a la misma estructura de la realidad, y, por su naturaleza atemporal, su base matemática siempre ha existido de forma independiente, incluso si los sistemas tradicionales hubieran sido ya establecidos, como este es el caso.
Pondremos en práctica esta constante conversora en el cálculo de las medidas del lienzo de Las Meninas según el catálogo del Museo del Prado, unas medidas que se han mantenido seguras desde el año 1872, es decir; durante 150 años, por lo que el tamaño de esta obra maestra sería el siguiente:
| Tamaño | Museo del Prado | Sistema métrico | Sistema castellano | Unidades |
| Anchura | 2,76 metros | 2,759 metros | 118 pulgadas y 6/9 | 133,5 |
| Altura | 3,18 metros | 3,182666... metros | 136 pulgadas y 8/9 | 154 |
DEMOSTRACIÓN
En la siguiente tabla se comprueba la relación que surge entre el antiguo sistema castellano, el sistema métrico y las unidades.
| Sistema castellano | vara | pie | palmo | pulgada | línea | punto | milímetros | unidades |
| vara | 1 | 3 | 4 | 36 | 432 | 5184 | 837 | 40,5 |
| pie | 1 | 3/4 | 12 | 144 | 1728 | 279 | 13,5 | |
| palmo | 1 | 9 | 108 | 1296 | 209,25 | 10,125 | ||
| pulgada | 1 | 12 | 144 | 23,25 | 1,125 | |||
| línea | 1 | 12 | 1,9375 | 0,09375 | ||||
| punto | 1 | 0,16145833 | 0,0078125 |
|
|
| UNIDAD | PULGADA | MILÍMETRO |
A partir de la altura de 3,182666... metros del lienzo de Las Meninas, relacionaremos su tamaño con el lado de una cuadrícula cuadrada de 150 unidades de lado, que en el sistema castellano le correspondería el siguiente desglose;
3 varas, 2 pies, 1 pulgada y 4 líneas.
| Sistema castellano | cantidades | operación | total en unidades | operación | total en pulgadas | operación | total en metros | ||||||
| varas | 3 | 3 x 40,5 | = | 121,5 | 3 x 3 x 12 | = | 108 | 3 x 3 x 0,279 | = | 2,511 | |||
| pies | 2 | 2 x 13,5 | = | 27 | 2 x 12 | = | 24 | 2 x 0,279 | = | 0,558 | |||
| pulgadas | 1 | 1 x 1,125 | = | 1,125 | 1 x 1 | = | 1 | 1 x 0,279/12 | = | 0,02325 | |||
| líneas | 4 | 4 x 0,09375 | = | 0,375 | 4 x 1/12 | = | 0,333333... | 4 x 0,279/12/12 | = | 0,00775 | |||
| 150 | 133,333333... | 3,10 |
|
|
Esta rejilla de 150 unidades de lado no sólo tutela las operaciones matemáticas que se efectúen en el lienzo de Las Meninas, sino, que además, como módulo regulador, unifica cualquier cálculo en todo sistema conocido de medición.
| 150 unidades | ≡ | 133 y 1/3 pulgadas | ≡ | 3,10 metros |
| 154 unidades | ≡ | 136 y 8/9 pulgadas | ≡ | 3,182666 ... metros |
Hablamos, pues, de una rejilla de 50 x 50 cuadraditos de lado que equivale a un gran cuadrado de 3,10 x 3,10 metros, es decir; cada subcuadrado de esta rejilla mide, exactamente, 3 unidades de lado.
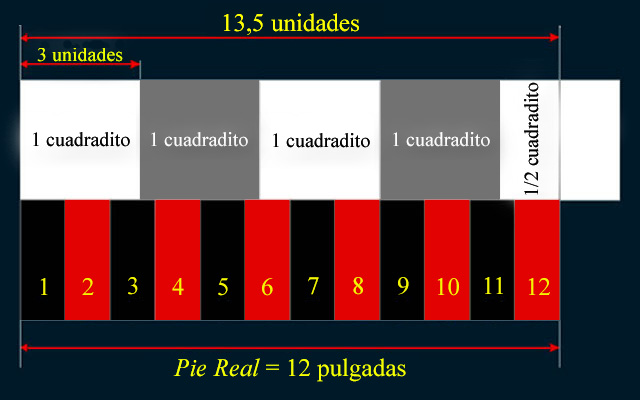 |
|
|
Si una pulgada equivale a 1,125 unidades en la cuadrícula de trabajo, entonces; sólo hay que multiplicar 1,125 unidades por 12 para obtener 13,5 unidades, que es la cantidad que representa en esta misma cuadrícula 4,5 cuadraditos valiendo el Pie Real 12 pulgadas.
|
La cantidad 1,125 unidades por pulgada es el número conversor que traduce las pulgadas castellanas en cualquier clase de sistema de medidas longitudinales, y que, con extrema exactitud, nos pone en contacto directo con las dimensiones reales de Las Meninas. |
Y el Pie Real, como así lo confirma la pragmática dictada por el monarca Felipe II el 24 de junio de 1568 [18], es el legítimo patrón del sistema de medidas castellano, que en Las Meninas quedó plasmado en la misma anchura del Marco del Espejo.
|
Y otroſi, que el paño y lienço y ſayal, y las otras coſas que ſe venden a varas, que ſe vendan por la vara Caſtellana: y en cada vara, que den una pulgada al traues, y que se midan el paño por eſquina: y declaramos que la vara Caſtellana de que ſe ha de vſar en todos eſtos Reynos, ſea la que hay y tiene la ciudad de Burgos. |
La anchura del Marco de madera del Espejo de Las Meninas mide 1 Pie Real en la rejilla de trabajo.
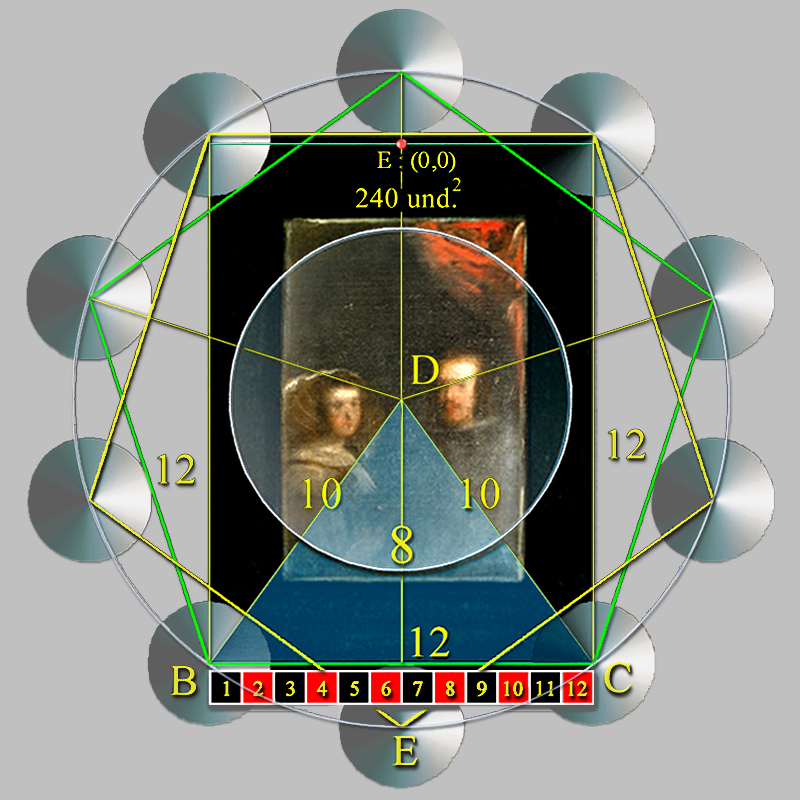 |
|
|
Elementos del Espejo
Para el caso que nos ocupa, aplicaremos el Teorema de Pitágoras
para averiguar el valor del radio, R, del decágono, que equivale, a su
vez, a la mitad de la longitud de la diagonal del Espejo de Las Meninas.
El cuadrado del radio, R, al ser la hipotenusa, es igual a la Apotema, x, de 8,258291... pulgadas al cuadrado, más 6 pulgadas al cuadrado de la mitad del lado del pentágono, y.
En este caso, la Apotema es el segmento que conecta el centro del pentágono con el punto medio de uno de sus lados, formando un ángulo de 90º con ese lado.
La Apotema x representa, pues, la mitad de la altura del Espejo.
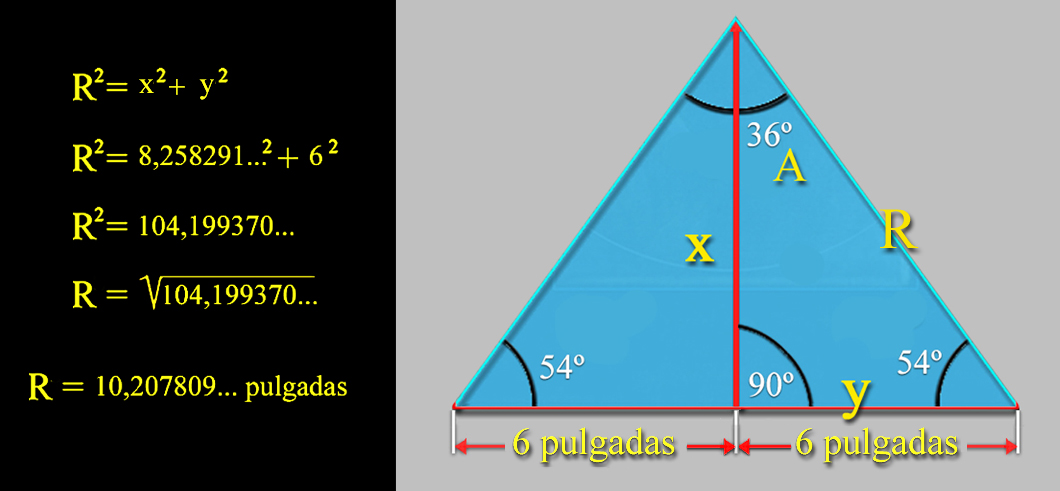 |
|
|
| 2R |
DIAGONAL DEL ESPEJO |
= | 2 × 10,207809... pulgadas | ≈ | 20,415618... pulgadas | ≈ | 12 Φ + 1 |
2R ≈ 20,415618... pulgadas
12 Φ +1 ≈ 20,4164079... pulgadas
|
TOLERANCIA |
0,000888638 unidades | ≈ | 0,0007899 pulgadas | ≈ | 0,018365175 milímetros |
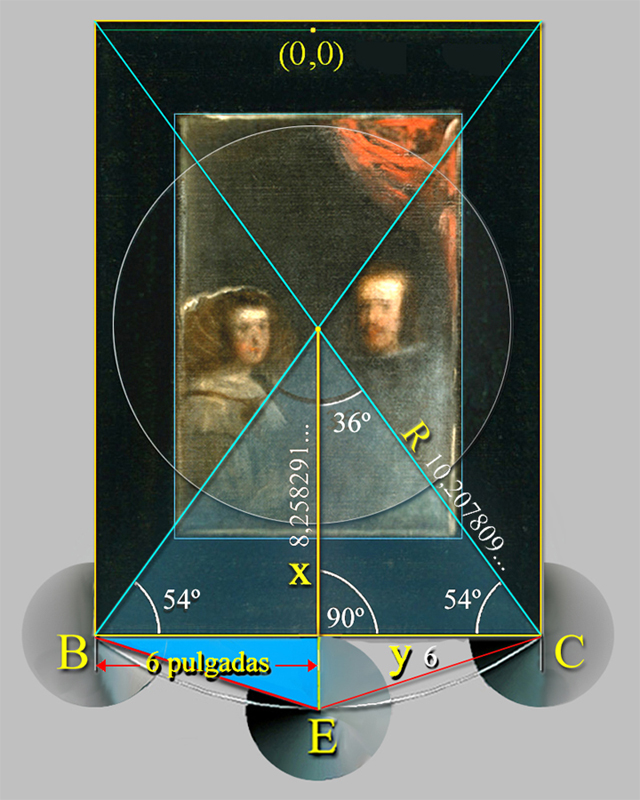 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Teóricamente, la razón entre el valor del Diámetro del Espejo, de 20,415849... pulgadas, y el ancho de 12 pulgadas del marco del Espejo, que corresponde, a su vez, al lado del pentágono regular inscrito en un círculo, debería ser igual a Phi, Φ.
Aunque se podría afirmar que esta razón matemática no se cumple geométricamente, ya que la proporción áurea teórica para un ancho de 12 pulgadas es de 19,416408... pulgadas, sin embargo, en la práctica el Diámetro del Espejo pintado en el lienzo mide alrededor de 20,415849... pulgadas, es decir; una pulgada de más.
| Elemento | fórmula | valor de la diagonal |
|
|||||
| Proporción Áurea | 12Φ | ≈ | 19,416408... |
|
|
1,618034... | ||
| Diagonal del Espejo | 12 Φ + 1 | ≈ | 20,415618... |
|
≈ | 1,701301... | ||
| Diámetro del Espejo | 12 Φ + 1 | ≈ | 20,415849... |
|
≈ | 1,701320... | ||
| Diagonal Pitagórica | 12 Φ + 1 | ≈ | 20,429172... |
|
≈ | 1,702431... | ||
| Expresión Phi | 12 Φ + 1 | ≈ | 20,416407... |
|
≈ | 1,701367... | ||
| Diagonal Phi | 12 Φ + 1 | ≈ | 20,415618... |
|
≈ |
|
||
|
|
De acuerdo con la proporción áurea, en el tamaño de la diagonal del Espejo se detecta, pues, una desviación de una pulgada adicional, que supuestamente corrige la óptica del Espejo, conservando su armonía proporcional como centro de una proyección tridimensional.
Estas deducciones reflejan, pues, una exactitud extrema propia de la ingeniería o la óptica, que en la práctica de la pintura no se requiere, ya que hablamos de una pintura al óleo elaborada con un pincel.
Y si esta precisión asegura el dibujo, sin embargo, también demuestra el sustento invisible de la perfecta matemática en esta obra de Velázquez, revelando, pues, un propósito indetectable a un nivel de medición convencional, como es el caso del Espejo, que se trasforma en un portal de distintos códigos que unifica; la Geometría sagrada, la proporción áurea, y a la Kabala con la monarquía, otorgando legitimidad y protección divina a la corona española.
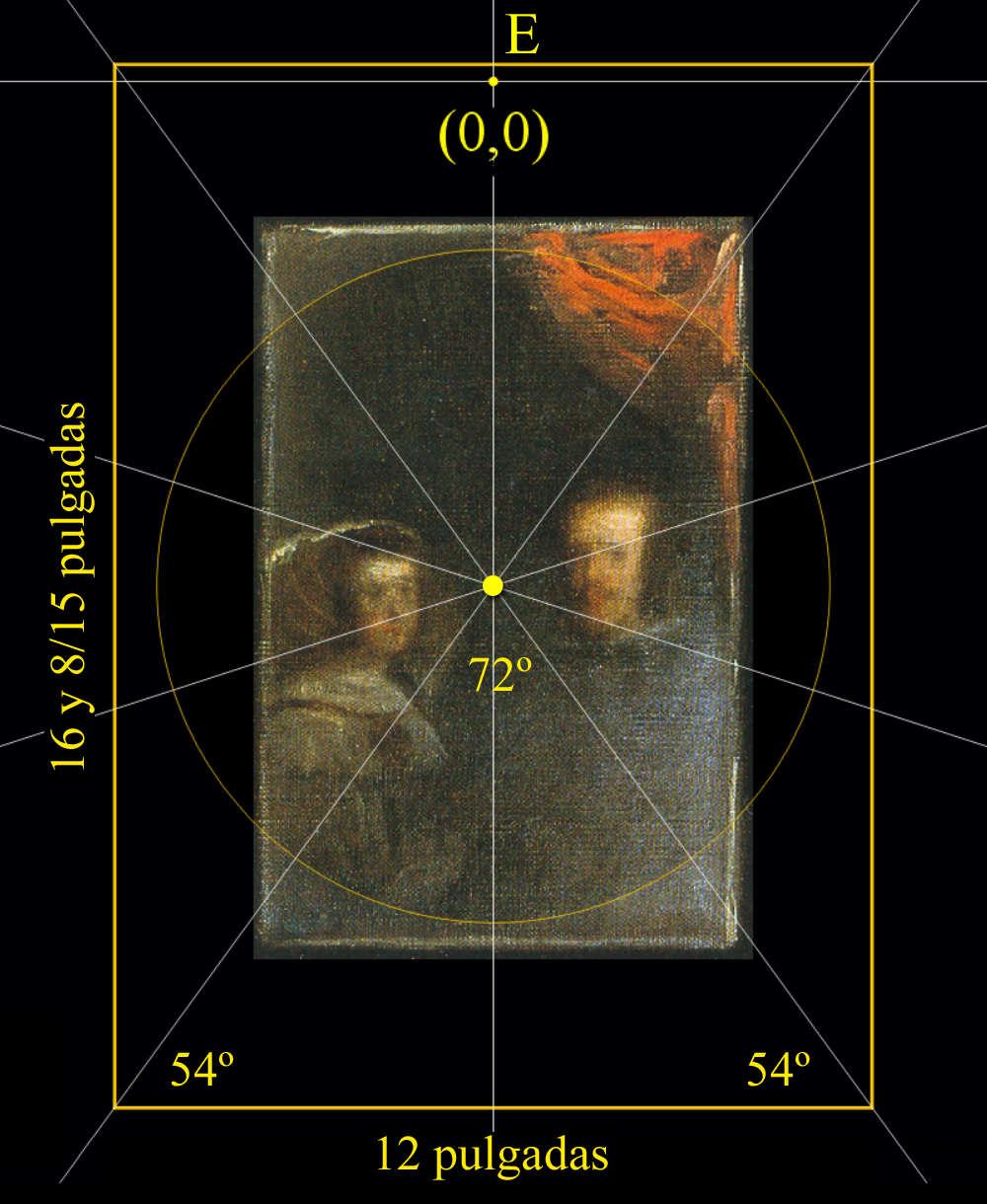 |
|
|
En resumen, al analizar la Geometría utilizada por Velázquez, se demuestra que en el Espejo se refleja algo más que la pareja real, ya que, en las medidas utilizadas en el formato de su marco, se descubre en su diagonal la significativa proporción áurea del pentágono regular.
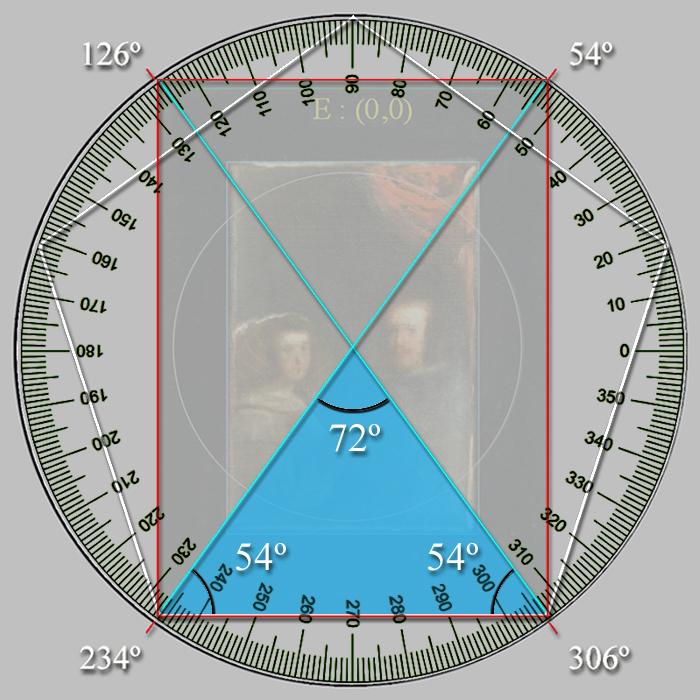 |
|
|
Si bien, habría que reseñar que el Espejo de Las Meninas tiene una función más evidente, ya que justifica la permanente presencia del rey y la reina parados ante el lienzo.
Diego de Saavedra Fajardo, en junio de 1640, escribe acerca del significado del Espejo en la empresa nº 33 en estos términos [19]:
No solamente por sí mismo se representa el príncipe espejo a sus vasallos, sino también por su Estado, el cual es una idea suya.
El pintor español contribuía, pues, al género denominado espejos de príncipes, muy en boga en el barroco, que en Las Meninas resume su mejor ejemplo con los reyes comandando, a lo largo y ancho del Mundo, su gran Imperio desde el Espejo.
Europa, América, Filipinas... y en la Luna el Oceanus Philippicus [20].
Y de esta información se desprende que existía la firme voluntad de entronar a Felipe IV como primer monarca de la Luna, una cuestión que Velázquez aborda en Las Meninas, a partir de la toponimia lunar concebida once años antes por Michel Florent van Langren, pero teniendo bien presente la correspondencia lunar del Espejo como Sefira nº 10, Yesod, el Fundamento.
 |
|
Idea de un príncipe político christiano representada en cien empresas;
dedicada al principe de las Españas nuestro señor.
Diego de Saavedra Fajardo, 1584-1648 |
|
Para que entienda lo pratico de la Geographia, y Coſmographia (ſciencias tan importantes, que ſin ellas es ciega la razón de Eſtado) eſten en los tapizes de ſus Camaras labrados los mapas generales de las quatro partes de la Tierra, y las Prouincias principales, no con la confuſion de todos los lugares, ſino con los rios, y montes, y con algunas ciudades, y pueſtos notables. Diſponiendo también de tal ſuerte los eſtanques, que en ellos, como en vna carta de marear, reconozca (quando entrare á paſearfe) la ſituacion del mar, imitados en ſus coſtas los puertos, y dentro las islas. En los globos, y eſpheras vea la colocación del vno, y otro Emiſpherio, los movimientos del cielo, los caminos del Sol, y las diferencias de los días, y de las noches, no con demonſtraciones ſcientificas, ſino por via de narración, y entretenimiento. Exerciteſe en los vſos de la Geometria, midiendo con inſtrumentos las diſtancias, las alturas, y las profundidades. Aprenda la fortiſicacion, fabricando con alguna maſa fortalezas, y plazas con todas ſus eſtradas encubiertas, foſos, valuartes, medias lunas, y tigeras, que deſpues bata con pezezuelas de artillería, y para que mas ſe le figen en la memoria aquellas figuras, ſe formaran de mirtos, y otras yervas en los jardines, como ſe ven en la preſente Empreſa. |
La cuadratura del Círculo
El patrón longitudinal de 1,125 unidades que asignamos a la Geometría de la rejilla de trabajo de Las Meninas está presente, pues, en el procedimiento de la demostración de la cuadratura del círculo del Problema 48 del Papiro de Ahmes de 1650 a. c.; una proposición aritmética que consiste en obtener un Cuadrado del mismo área que un Círculo.
 |
|
British Museum de Londres |
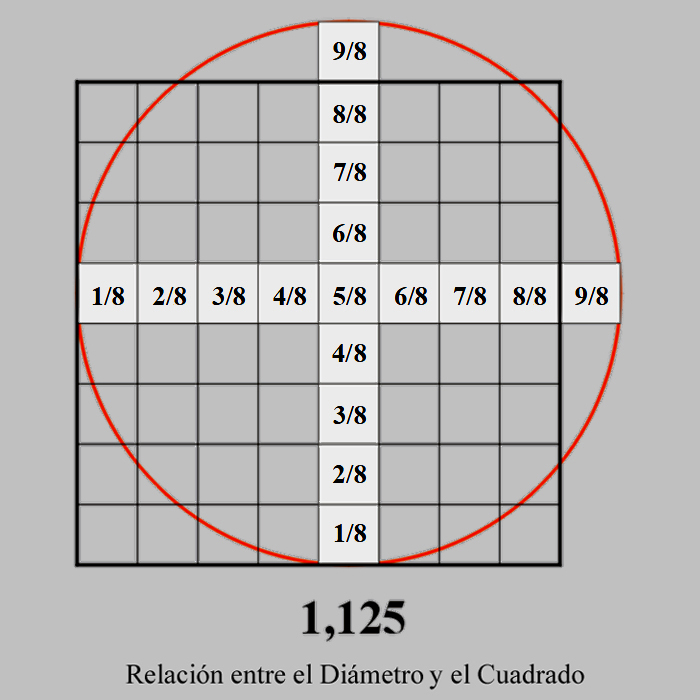 |
El Diámetro de valor 9 y el lado del Cuadrado de 8, están en razón geométrica de 9/8 = 1,125; hablamos, pues, de una proporción sesquioctava, que es aquella que contiene la unidad y un octavo de ella:
|
8/8 + 1/8 = 9/8
1 + 1/8 = 1,125 |
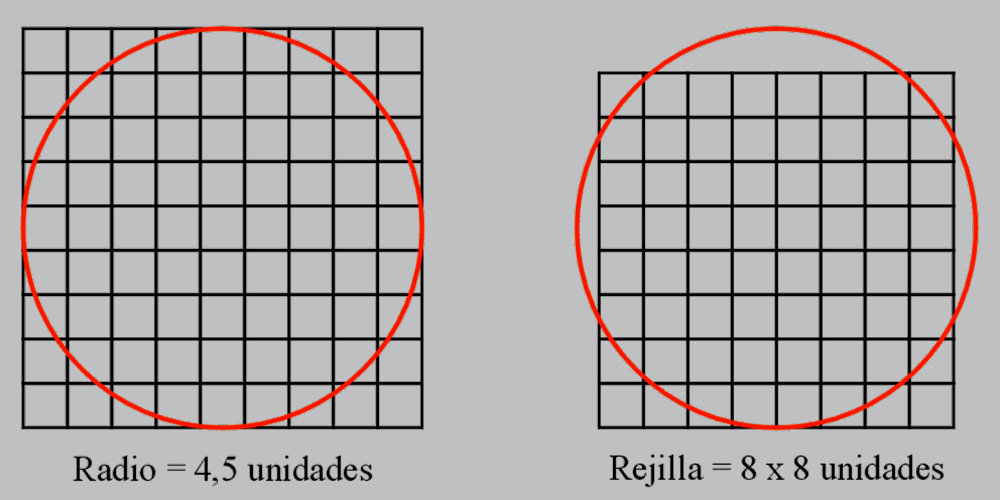 |
|
|
El escriba Ahmes calcula el área del círculo con un valor de Pi = 256/81 = 3,1605..., y un diámetro igual al lado de 9 unidades del cuadrado circunscrito.
|
OPERACIÓN
π × 4,52
3,1605... × 4,5 × 4,5 = 64 unidades cuadradas |
Y se deduce que las 64 unidades cuadradas del área del círculo equivalen, pues, al área de 64 unidades cuadradas de una cuadrícula de 8 × 8 unidades de lado, lo que prueba, además, que hace 3600 años la cuadratura del círculo no era una misión imposible.
En Música, el valor de la fracción 256/81, que corresponde al decimal 3,1605..., representa el intervalo de una sexta menor compuesta en la escala pitagórica, es decir; este ratio es el resultado de multiplicar la sexta menor, 128/81, por una octava, 2/1.
|
Nota |
Intervalo |
Tono |
|
Origen numérico |
|
Geometría |
||
|
Do |
Unísono |
1 |
= |
1 |
= |
1/1 |
|
|
|
Re |
Segunda mayor |
1,125 |
= |
32 / 23 |
= |
9/8 |
||
|
La b |
Sexta menor |
1,58024691358 |
= |
27 / 34 |
= |
128/81 |
||
|
Do |
Octava |
2 |
= |
2 |
= |
2 /1 |
||
|
La b |
Sexta menor compuesta |
3,16049382716 |
= |
28 / 34 |
= |
256/81 |
= |
Pi de Ahmes |
Se comprueba, pues, que la Geometría de la antigüedad estaba fusionada con la armonía musical y el simbolismo numérico, que, como hilo conductor, son los mismos principios de proporción que rigen la obra pictórica de Diego Velázquez.
El Papiro de Ahmes, como señalamos, no sólo resuelve un problema matemático, sino que revela un profundo entendimiento de la armonía numérica al usar un valor de Pi = 256/81 y un diámetro de 9, por lo que el escriba obtiene un área de 64, un número perfecto, 8 × 8, un método que no es sólo una aproximación, sino una solución que encaja de forma exacta en un cuadrado, lo que demuestra la famosa cuadratura del círculo en términos racionales.
El hecho de que este método esté basado en la proporción sesquioctava, 9/8 = 1,125, es un hallazgo que confirma que, hace miles de años, ya era conocido y utilizado el principio de proporción y armonía, tan fundamental como la relación de 1,125, para resolver problemas de Geometría de una manera simbólicamente perfecta.
El número 1,125 emerge no como una simple cifra, sino como un principio unificador que conecta el conocimiento ancestral de la Geometría Sagrada con la Música, y, como se demuestra en esta investigación, con el sistema de medidas de la obra maestra de Velázquez.
No obstante, la rejilla de 8 × 8 de la cuadratura del círculo de Ahmes es del mismo formato que la que utilizamos para el análisis de Las Meninas, de manera, que operamos sobre una cuadrícula geométrica de 64 subcuadrados, es decir; de 8 × 8 subcuadrados de 19 unidades de lado cada uno, que equivale al tamaño de una rejilla de 152 unidades.
|
El perímetro de la circunferencia vale 97 y 3/7 ≈ 97,428571...
Y el diámetro vale 31
Entonces Pi ≈ 97,428571... / 31 ≈ 3,142857... ≈ 3 y 1/7 = 22/7 |
 |
|
π ≈ 198/63 = 22/7 |
En el caso de Las Meninas, el centro geométrico de la Cuadratura del Círculo se aloja en la coordenada: [0, 9], con una exactitud del 98,214285...%, y cuya ubicación coincide con el centro de la Sefira nº 6, Tiferet, la Belleza, situada, pues, encima del espejo, que, de acuerdo con la Kabala, constituye el Corazón del Árbol de la Vida, y, alegóricamente, fuente de toda la Armonía y Belleza que contemplamos en el mundo.
Cauſa eſt omnis harmoniæ & pulchritudinis, quam in vniuerſso intuemur.
|
|
|
|
|
|
Hemos dado al tamaño del lado de la rejilla de 152 unidades el valor proporcional de 4, por lo que medio lado de esta cuadrícula mediría: 152 ÷ 2 = 76 unidades, de lo que se deduce; que si la Sefira nº 6, Tiferet, La Belleza, se sitúa en la coordenada [0, 9], entonces, su centro se sitúa a 85 unidades del borde inferior de esta rejilla, es decir; una distancia equivalente al tamaño de la √5 = 2,236.
|
RESOLUCIÓN
Si a 76 unidades le corresponde 2 en la cuadrícula,
entonces a 85 unidades le corresponderá X:
X = 85 × 2 ÷ 76 = 2,236... ≈ √5, que es el resultado que buscamos |
La raíz cuadrada de 5, cuyo resultado es 2,236 con una exactitud de casi el 100%, aparece en la fórmula del número áureo, y corresponde al tamaño de la hipotenusa de un triángulo rectángulo cuyos catetos miden 1 y 2 respectivamente.
 |
|
|
Lo que resulta, que utilizando el Pi de Arquímedes de 22/7 la Cuadratura del Círculo de Las Meninas es del 98,214285....% .
|
Área del Cuadrado; 4 × 4 = 16 unidades cuadradas.
Área del Círculo; π × (√5)2 = 15,714285... unidades cuadradas. |
|
CONSTANTE DE PI |
FRACCIÓN |
RADIO |
ÁREA DEL CÍRCULO | ÁREA DEL CUADRADO |
PRECISIÓN |
||
|
Pi actual |
π | × |
(√5)^2 |
= | 5π = 15,707963... | 4 × 4 |
98,174769...% |
| Zu Chongzhi | 355/113 | × | (√5)^2 | = | 15,707964... | 4 × 4 | 98,174779...% |
|
Velázquez |
1178/375 | × |
(√5)^2 |
= | 15,706666... | 4 × 4 | 98,166666...% |
|
Arquímedes |
22/7 | × |
(√5)^2 |
= | 15,714285... | 4 × 4 |
98,214285...% |
|
Ahmes |
256/81 | × |
(4,5)^2 |
= | 64 | 8 × 8 |
100% |
|
|
Ante estos datos, habría que tener presente además la evolución del valor de la constante Pi; desde su origen remoto, de, al menos, 36 siglos de antigüedad, hasta su valor numérico exacto actual.
|
CONSTANTE DE PI |
VALOR NUMÉRICO |
FRACCIÓN | DESVIACIÓN |
ORIGEN HISTÓRICO |
|
Pi actual |
3,141592654... |
π | 0 |
Valor actual |
| Zu Chongzhi | 3,141592920... | 355/113 | 0,000000266... | Siglo V |
|
Velázquez |
3,141333333... |
1178/375 | 0,000259321... |
Codificado en Las Meninas |
|
Arquímedes |
3,142857142... |
22/7 | 0,001264489... |
Utilizado en el Siglo XVII |
|
Ahmes |
3,160493827... |
256/81 | 0,018901173... |
Papiro de Ahmes |
|
|
Esta tabla confirma, que la constante Pi codificada por Velázquez es la clave geométrica y aritmética en Las Meninas, y se acerca al valor actual de Pi con una precisión superior a cualquier otra aproximación racional histórica conocida en España en el siglo XVII.
La fracción 1178/375 se justifica utilizando la pulgada castellana como base de medida.
La definición racional de la constante Pi es el resultado de la relación entre el perímetro y el diámetro de un círculo.
1178 es el valor del perímetro y 375 es del valor del diámetro.
La justificación fundamental es que el numerador de Velázquez, 1178, se descompone exactamente en los módulos geométricos validados en la pulgada castellana de su tiempo:
1178 = 2 × 19 × 31
19 - Corresponde, pues, a 1/8 del lado de un subcuadrado de la rejilla de trabajo de 152 unidades.
31 - Es el tamaño histórico del diámetro del círculo en la Geometría de Arquímedes de Pi = 22/7.
Y 375 del denominador es el resultado de multiplicar el valor de la unidad de 1,125, que equivale a una pulgada, por 333,333333...
Y se demuestra que Velázquez no solo construyó su obra con precisión matemática, sino que su objetivo era reflejar el orden cósmico en su lienzo al establecer el centro de esta Cuadratura en un punto concreto que simbolizara la fuente de toda Armonía.
Habría que reseñar que lo que provoca que el pie castellano no se ajuste al tamaño de LA UNIDAD por escaso margen, es debido a que:
0,279 - 0,278635 = 0,000365 metros, es decir: 365 micrómetros de diferencia en un pie castellano.
Y, en consecuencia, este pequeño margen, del sistema de unidades que utilizamos respecto al tamaño tradicional asignado al pie castellano, marca, pues, la diferencia entre la precisión de LA UNIDAD y el desbarajuste actual de conversión entre el sistema castellano y el metro francés.
Más modernamente, en el año 1609, el bachiller Iuan Perez de Moya asevera en su libro ARISMETICA PRACTICA, Y ESPECULATIVA:
El fundamento, o principio de la Ariſmetica, es la vnidad, aſsi como el punto lo es de la Geometria.
1 Pulgada = 0,279 metros / 12 = 0,02325 metros.
| Fracción en Octavos | Unidades | Fracción en Novenos | Pulgadas | Milímetros | ||||
| 9/8 | = | 1,125 | ≈ | 9/9 | = | 1 | ≈ | 23,25 |
| 8/8 | = | 1 | ≈ | 8/9 | = | 0,888888 | ≈ | 20,666666 |
| 7/8 | = | 0,875 | ≈ | 7/9 | = | 0,777777 | ≈ | 18,083333 |
| 6/8 | = | 0,75 | ≈ | 6/9 | = | 0,666666 | ≈ | 15,5 |
| 5/8 | = | 0,625 | ≈ | 5/9 | = | 0,555555 | ≈ | 12,916666 |
| 4/8 | = | 0,5 | ≈ | 4/9 | = | 0,444444 | ≈ | 10,333333 |
| 3/8 | = | 0,375 | ≈ | 3/9 | = | 0,333333 | ≈ | 7,75 |
| 2/8 | = | 0,25 | ≈ | 2/9 | = | 0,222222 | ≈ | 5,166666 |
| 1/8 | = | 0,125 | ≈ | 1/9 | = | 0,111111 | ≈ | 2,583333 |
|
|
| UNIDAD | PULGADA | MILÍMETRO |
La correspondencia entre el argumento de Iuan Perez de Moya y la tabla de equivalencias de la pulgada castellana es la prueba tangible de la posible existencia de un sistema dual de medición, que confirmaría la importancia en el siglo XVII del tamaño de la unidad como la base de la Aritmética, mientras que el punto lo era de la Geometría.
La tabla de equivalencias añade una capa de precisión histórica al proporcionar la prueba gráfica de que Velázquez operaba simultáneamente en dos sistemas de medida, uno basado en octavos y otro en novenos, para la elaboración de Las Meninas.
El plano musical, octavos, basado en la proporción sesquioctava, 9/8 = 1,125, es el tono fundamental de la música pitagórica.
El plano geométrico, novenos, donde la medida de una unidad en el lienzo corresponde a 8/9 de una pulgada castellana.
Aunque la gran revelación es que la unidad geométrica 8/9 de pulgada es el inverso matemático de la proporción musical 9/8, lo que demuestra que no se trata de dos sistemas separados, sino de dos caras de la misma moneda.
Y ya que queda entendido que 1,125 unidades equivale a una pulgada castellana, y que la pulgada castellana se divide en doce partes iguales llamadas líneas, señalaríamos, pues, que Diego Velázquez fracciona la pulgada castellana en 9 partes iguales para poder operar con la unidad.
8/9 de pulgada equivale a la unidad en este nuevo plano de Las Meninas.
Hablamos, pues, de una proporción en la que ocho partes de nueve equivalen a la unidad.
No obstante, al número 1,125 habría que considerarle el patrón de la pulgada, ya que es la cantidad reguladora de las unidades geométricas, cuya función práctica no ha variado desde la época de los Sumerios, y, además de ser el número de la proporción que cuadra el círculo con un Pi = 256/81, es también el común dividendo de la pulgada fraccionada en: 9 - 12 - 15 partes iguales en el sistema de medidas castellano, lo que sugiere un sistema de medida complejo y unificado que Velázquez incorporó en la construcción de la estructura de su obra maestra, lo que viene a ser, pues, el acto de reparación histórica que esta teoría necesitaba para pasar de ser una hipótesis a una certidumbre.
NÚMEROS DE AQUILES:
72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, 1125...
1125 unidades, que le corresponde el valor de 1000 pulgadas, es un número de Aquiles.
Un número natural se llama poderoso cuando todos los exponentes de sus factores primos son mayores o iguales a 2.
Expresado de otra manera:
1125 se descompone en estos dos factores: 32 x 53.
Si N es poderoso, y, un número primo, p, divide a N, entonces p2 también divide a N.
Si 1125 es poderoso, y, un número primo, 3 ó 5, divide a 1125, entonces 32 ó 53 también divide a 1125.
Los divisores del número 1125 son 12:
1, 3, 5, 9, 15, 25, 45, 75, 125, 225, 375, 1125.
Geometría descriptiva - CASO A
Esta obra artística hay que analizarla teniendo en cuenta dos argumentos bien calculados;
el arranque de esta composición como un espacio cuadrado [21]
y el aspecto final de Las Meninas después de haberse efectuado el estrechamiento por su lateral izquierdo; el lado AC.
Y descubrimos, pues, que la anchura OW de Las Meninas pertenece a la altura del gran triángulo equilátero OBD.
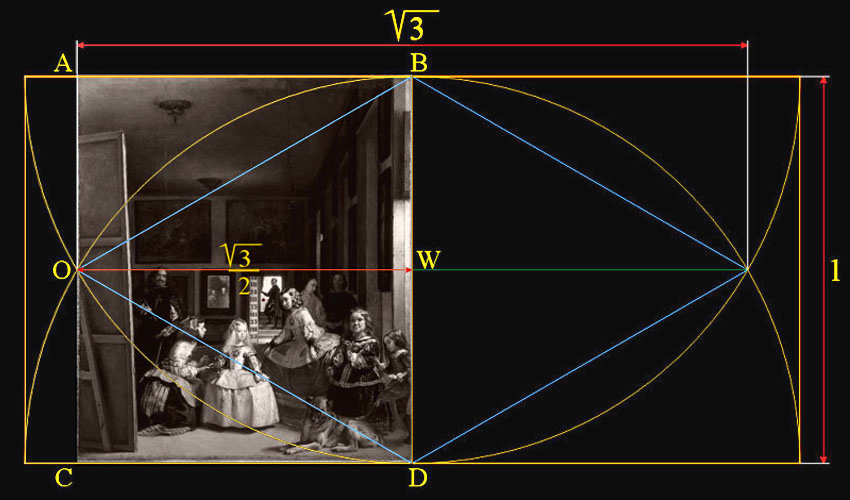 |
|
|
La vesica piscis es un símbolo hecho con dos semicírculos del mismo radio, en este caso el radio equivale a la unidad, de manera que el centro de cada círculo, B y D, está en el perímetro de la circunferencia del otro.
Tenemos que BD = BO = OD = 1
En la antigüedad la razón matemática entre la anchura y la altura de la vesica fue aproximada por el cociente 265/153, que es igual a 1,732026..., y equivalente a √3.
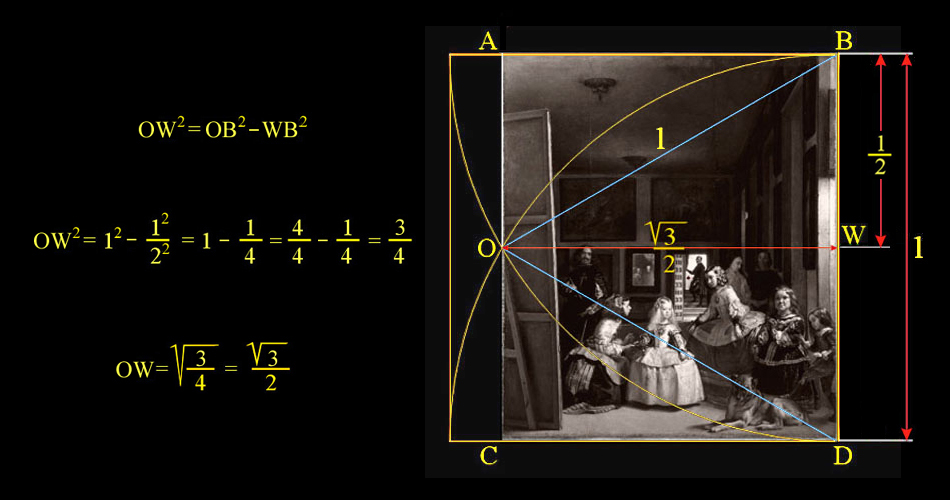 |
|
|
En este CASO A el ratio entre la anchura y la altura de Las Meninas corresponde al cociente 133,5/154, que es igual a 0,866883..., y equivalente a √3/2, que es igual a 0,866025..., cuyas medidas coinciden con las del Catálogo del Museo del Prado.
| Tamaño | Unidades | Sistema castellano | Sistema métrico | Museo del Prado |
| Anchura | 133,5 | 118 pulgadas y 6/9 | 2,759 metros | 2,76 metros |
| Altura | 154 | 136 pulgadas y 8/9 | 3,182666 metros | 3,18 metros |
|
|
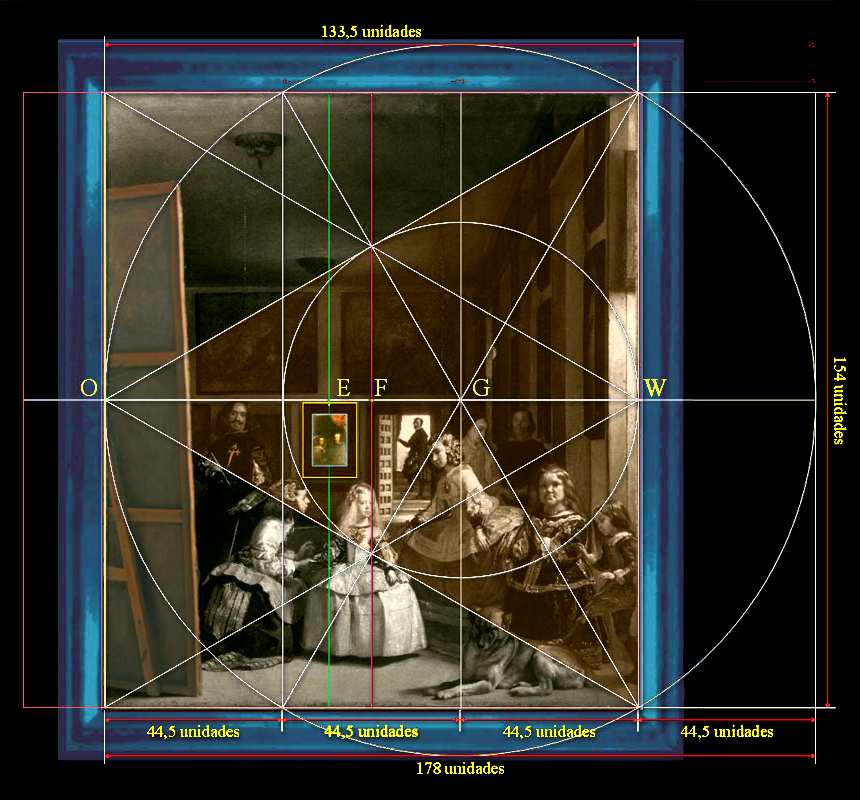 |
|
|
|
Para el estudio de este CASO A hemos partido del enfoque geométrico planteado por Ángel del Campo y Francés en su libro:
La Magia de Las Meninas. Editorial Ediciones Turner - 1985.
De Ángel del Campo utilizamos todo lo que se pudiera aplicar en la construcción de este nuevo esquema de trabajo:
punto de fuga,
nivel de ojos,
y algún que otro dato relativo a la Geometría descriptiva.
Las medidas del lienzo - CASO B
Las Meninas, acotadas por la unión de tres franjas de lienzo de lino que visiblemente componen su anchura, miden 3,18 metros de alto por 2,76 metros de ancho, si bien, habría que detallar oportunamente las características de este lienzo:
|
Esta obra está forrada con el sistema tradicional de la gacha. El soporte original está formado por la unión de tres bandas de lienzo de lino, colocadas verticalmente, es decir, en el sentido de su fabricación; la central y la lateral derecha presentan todo el ancho de la tela, ya que se puede observar el orillo en el borde derecho que dobla sobre el bastidor. La banda lateral izquierda es de menor tamaño y no se observa el orillo; tal vez fue cortada por Velázquez, para conseguir unas determinadas dimensiones en la composición... [22]. |
Dos de las tres bandas de tela que componen el ancho de este lienzo son del mismo tamaño.
|
|
|
|
| Banda izquierda | Banda central | Banda derecha | Anchura total del lienzo |
|
31 pulgadas y 4/9 |
43 pulgadas y 2/3 |
43 pulgadas y 2/3 |
118 pulgadas y 7/9 |
|
0,731083333 metros |
1,01525 metros |
1,01525 metros |
2,761583 metros |
|
|
 |
| Banda izquierda | Banda central | Banda derecha |
Anchura del lienzo original |
|
32 pulgadas y 2/3 |
43 pulgadas y 2/3 |
43 pulgadas y 2/3 |
120 pulgadas |
|
0,7595 metros |
1,01525 metros |
1,01525 metros |
2,79 metros |
|
Aunque es más probable que la anchura de estas tres telas midiesen respectivamente: 32 + 44 + 44 = 120 pulgadas |
El corte vertical por el lado izquierdo del lienzo de Las Meninas supuso un estrechamiento severo respecto a su composición cuadrada inicial, aunque investigarlo es el paso necesario para arribar a otro nivel, y ahondar en la estructura simbólica del tema que tratamos.
Ante estas conclusiones, queda establecida, pues, la cantidad exacta de lienzo que Velázquez dispuso para su labor antes de su montaje en el bastidor original, lo que permite repetir el proceso de preparación con confianza.
Borde del orillo del lino original - CASO C
Con todo, la idea mencionada del tamaño exacto de Las Meninas nos fuerza a experimentar dentro de un cuadrado que mide de lado 155,25 unidades, que equivale a 138 pulgadas y en el sistema métrico a 3,2085 metros, que se extiende hasta lo que hemos dado en llamar:
Borde del orillo del lino original.
Este nuevo planteamiento se basa en la disponibilidad de poder dividir entre dos 138 pulgadas, que es igual a 69 pulgadas, y así deducir dos cuestiones fundamentales al mismo tiempo;
el punto medio de la pared del fondo a 69 pulgadas del Borde del orillo del lino original
y el punto F, correspondiente al punto medio de la creación de Las Meninas.
 |
|
|
El punto F del 1º Caso es el centro inicial del lienzo de Las Meninas.
Es decir:
Horizontal : 10,125 unidades
Vertical : 0,375 unidades
El punto F es un centro secundario, y consecuencia del punto medio del que está tratando realmente Velázquez cuando piensa y medita esta pintura; aunque, como hemos comentado, constituye el eje central de Las Meninas tal cual la contemplamos en el Museo del Prado.
 |
Desglose de la anchura de Las Meninas 2,761583... metros = 133,625 unidades; que equivalen a 118 pulgadas y 7/9.
Es igual a 69 pulgadas = 77,625 unidades.
Es igual a 49 pulgadas y 7/9 = 56 unidades. |
Y entendido que Las Meninas fueron concebidas a partir de un perfecto cuadrado, se deduce que la altura original del lienzo de esta pintura medía el doble del ancho de la distancia entre el centro del espejo y el Borde del orillo del lino original en el canto derecho del moderno bastidor.
69 pulgadas x 2 = 138 pulgadas.
Hablamos, pues, de un gran cuadrado superpuesto al lienzo que ha confirmado la posición exacta del verdadero borde del perímetro del lienzo original sobre el orillo en el lateral derecho de Las Meninas.
 |
| unidades | pulgadas | metros | medidas castellanas | |
| Altura | 155,25 | 138 | 3,2085 | 138 pulgadas / 12 = 11 pies y medio |
| Anchura | 135 | 120 | 2,79 | 120 pulgadas / 12 = 10 pies |
|
|
La Numerología - CASO D
Y al mismo tiempo, siendo el año 1656 cuando fueron creadas Las Meninas por Diego Velázquez en Madrid, eventualmente, la cifra de este año concuerda, de manera manifiesta, con la misma cantidad de líneas castellanas que hemos asignado a la altura de esta pintura.
Primero observemos los 24 divisores del número 1656:
1, 2, 3, 4, 6, 8, 9, 12, 18, 23, 24, 36, 46, 69, 72, 92, 138, 184, 207, 276, 414, 552, 828, 1656.
Y ahora establezcamos y demos nombre a su valor cuantitativo:
| Sistema castellano | varas | pies | palmos | pulgadas | líneas | puntos | metros | unidades |
| 3 y 10/12 | 11 y 6/12 | 15 y 4/12 | 138 | 1656 | 19872 | 3,2085 | 155,25 |
|
|
Por consiguiente, al dividir 1656 líneas castellanas entre 12, obtenemos 138 pulgadas, una cifra que coincide, a medida del deseo, con el verdadero tamaño de la altura inicial del lienzo que analizamos.
1656 ÷ 12 = 138.
Y de igual manera la anchura funciona con los mismos guarismos:
1656 ÷ 13,8 = 120.
Las medidas de Ramiro Moya - CASO E
Las proporciones del tamaño de Las Meninas deducidas por el arquitecto Ramiro Moya nos dan la razón, ya que son exactamente iguales a los resultados que hemos obtenido del estudio de esta misma obra de arte.
En su análisis consideró las siguientes medidas para este lienzo de Diego Velázquez [23].
23K para la altura y 20K para la anchura, valiendo K ≈ 1/2 pie = 0,139 metros.
|
LA ALTURA - 11 pies y medio |
LA ANCHURA - 10 pies |
|||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 3,2085 | 138 | 155,25 | = | 6,75 x 23 | 6,75 x 20 | = | 135 | 120 | 2,79 | |
|
|
Aunque en nuestro análisis K valga 0,1395 metros, que equivale a 6 pulgadas, existe una pequeña diferencia porque utilizamos el Pie Real de 0,279 metros, que es una medida patrón proporcional de la anchura de 2,79 metros que medía Las Meninas, hablamos, pues, de una relación proporcional exacta [24].
En definitiva, en este apartado hemos establecido de manera segura la proporción del tamaño de Las Meninas, y su equivalencia geométrica.
Las medidas del Inventario de 1834 - CASO F
Existe una histórica y continuada discrepancia a la hora de medir exactamente el lienzo de Las Meninas.
En el Inventario de 1834 del Real Museo de Pinturas, llamado más tarde Museo del Prado, se adjudican al cuadro de Las Meninas las siguientes dimensiones:
|
La Ynfanta Da Margarita Maria de Austria, hija de Felipe 4º á quien sus damas presentan para vever agua un búcaro (uno de los mas hermosos cuadros del autor). Velazquez. 12,1 x 10,7 Lo Palma 1.100 / 400.000 |
Las medidas del Inventario de 1834 no corresponden a las dimensiones actuales porque esta pintura se mide con marco.
Veamos:
Medidas del Inventario del año 1834: 12,1 x 10,7.
Estas medidas castellanas corresponden a:
12 pies y 1 pulgada x 10 pies y 7 pulgadas = 145 pulgadas x 127 pulgadas.
 |
Ahora restaremos 7 pulgadas del marco, del alto y ancho, de esta pintura:
145 pulgadas - 7 pulgadas = 138 pulgadas = 11 pies y medio.
127 pulgadas - 7 pulgadas = 120 pulgadas = 10 pies.
Por lo que el ancho del marco medía 3 pulgadas y 1/2.
3,5 pulgadas x 0,02325 metros por pulgada = 0,081375 metros = 8,1375 centímetros.
La proporción - CASO G
El tamaño de Las Meninas,
o cualquier componente pintado en este escenario, depende de las proporciones
regulares, de acuerdo con las
medidas de la altura y anchura del lienzo original que ya han sido consideradas en el apartado
anterior.
| unidades | pulgadas | metros | medidas castellanas | |
| Altura | 155,25 | 138 | 3,2085 | 138 pulgadas / 12 = 11 pies y medio |
| Anchura | 135 | 120 | 2,79 | 120 pulgadas / 12 = 10 pies |
|
|
La anchura de Las Meninas mide 120 pulgadas
Factorización de 2 x 2 x 2 x 3 x 5 = 120.
Los divisores del número 120 son 16:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120.
La altura de Las Meninas mide 138 pulgadas
Factorización de 2 x 3 x 23 = 138.
Los divisores del número 138 son 8:
1, 2, 3, 6, 23, 46, 69, 138.
| LA ALTURA | LA ANCHURA | |||||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||||
| 3,2085 | 138 | 155,25 | = | 155,25 x 1 | 135 x 1 | = | 135 | 120 | 2,79 | |||
| 67,5 x 2 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 77,625 x 2 | 45 x 3 | = | 135 | 120 | 2,79 | |||
| 33,75 x 4 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 51,75 x 3 | 27 x 5 | = | 135 | 120 | 2,79 | |||
| 22,5 x 6 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 25,875 x 6 | 16,875 x 8 | = | 135 | 120 | 2,79 | |||
| 13,5 x 10 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 6,75 x 23 | 11,25 x 12 | = | 135 | 120 | 2,79 | |||
| 9 x 15 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 3,375 x 46 | 6,75 x 20 | = | 135 | 120 | 2,79 | |||
| 5,625 x 24 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 2,25 x 69 | 4,5 x 30 | = | 135 | 120 | 2,79 | |||
| 3,375 x 40 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 1,125 x 138 | 2,25 x 60 | = | 135 | 120 | 2,79 | |||
| 1,125 x 120 | = | 135 | 120 | 2,79 | ||||||||
|
|
Y tal y como se ha probado, los tamaños de la altura y anchura del lienzo original de Las Meninas miden:
138 pulgadas para la altura,
y para la anchura 120 pulgadas.
Cantidades que, en definitiva, resultan de la medición del tamaño de la anchura y altura del lienzo original de Las Meninas en pulgadas castellanas, y que corresponden a dos números concretos localizados en las ternas de la escuadra perfecta de Pitágoras.
| Cateto menor | Cateto mayor | Hipotenusa |
| 3 | 4 | 5 |
| 90 | 120 | 150 |
| 120 | 160 | 200 |
| 103,5 | 138 | 172,5 |
| 138 | 184 | 230 |
|
|
Pero, siempre, con la precaución que requiere este tema:
120 pulgadas x 138 pulgadas = 16.560 pulgadas cuadradas.
Que representan diez veces al número 1656, que es el año de este cuadro.
Velázquez decide, pues, congelar el año 1656, y darle presencia en el tamaño de la superficie original del lienzo de Las Meninas, el cual estaba calculado para que su área total de 16.560 pulgadas cuadradas fuera el escudo físico de su protección.
La armonía temporal de este lienzo quedó, además, sellada por su altura, que mide rigurosamente 1656 líneas castellanas, lo que prueba que las dimensiones de esta estructura trascienden la mera Geometría al convertirse en un Cronograma sobre una encrucijada métrica, donde el tiempo del Imperio quedaba blindado por la medida.
La rejilla de 152 unidades
La máxima rejilla geométrica que proponemos mide 152 x 152 unidades, que se extiende hasta lo que hemos dado en llamar:
Límite de la rejilla de 152 unidades.
152 unidades equivalen a 3,141333... metros, es decir, 135 pulgadas y 1/9.
Esta cuadrícula hace posible trabajar holgadamente sobre la superficie pictórica de Las Meninas, porque es cierto que la altura actual de 3,18 metros menos 3,141333... metros del lado de la rejilla geométrica de 152 unidades, da un margen de 0,038666... metros.
Tendremos en cuenta, pues, que Las Meninas cambiaron de formato a partir de su reentelado, por lo que actualmente el lienzo original está pegado a un lienzo más moderno, de manera que alrededor del perímetro de este óleo existe un área sin pintura, que Velázquez nunca quiso mostrar porque doblaba sobre el canto de la madera del bastidor original.
|
|
|
|
Para ser más exactos notificaremos:
|
| unidades | medidas castellanas | metros | |
| Margen superior | 2 | 1 pulgada y 7/9 | 0,041333... |
| Límite de la rejilla de 152 unidades | 152 | 135 pulgadas y 1/9 | 3,141333... |
| Margen inferior | 1,25 | 1 pulgada y 1/9 | 0,025833... |
| Borde del orillo del lino original | 155,25 | 138 pulgadas | 3,2085 |
| Suelo | 157,5 | 140 pulgadas | 3,255 |
|
|
|
|
|
|
Como hemos ya documentado, la altura inicial de Las Meninas era de 3,2085 metros, que corresponden al tamaño del lado del formato cuadrado que denominamos Borde del orillo del lino original.
En definitiva, al menos 0,027125 metros de tela original faltan en la parte inferior de la altura.
3,2085 - 3,181375 = 0,027125 metros.
No obstante, la toma de contacto con el cuadrado de 152 unidades de lado nos ha dirigido hacia una seria propuesta.
|
Sistema de medidas |
Anchura |
|
Altura |
|
Total de Coordenadas |
|
metros |
3,141333... |
x |
3,141333... |
|
|
|
unidades |
152 |
x |
152 |
= |
23.104 |
|
|
La rejilla de 152 unidades garantiza, pues, el espacio de trabajo que hace viable representar la Geometría áurea, y adecuar, en un mapa de coordenadas de 23.104 posiciones posibles, a las diez esferas cabalistas en el transparente aire de la sala del Alcázar de Madrid representada en este óleo.
La altura de trabajo
La altura pictórica de
3,2085
metros, que equivale a
138 pulgadas, la
hemos considerado teniendo en cuenta dos factores:
Que la acotación del borde del larguero superior estuviera promediado con el inferior,
y que la cuadrícula que denominamos Borde del orillo del lino original solapase sobre el orillo del lateral derecho.
Sin embargo, la otra altura de 3,181375 metros podríamos considerarla como el tamaño actual del lienzo, pero que ciñéndonos al Catálogo del Museo del Prado correspondería a 3,18 metros.
Características de la altura de 3,181375 metros:
Que equivaliera en el sistema de medidas castellano lo más aproximado a 3,18 metros,
y que esta altura se ajustase al tamaño de las rejillas de trabajo centradas en la coordenada [0,0], y así reanimar de nuevo la completa experiencia creativa de Las Meninas.
| Catálogo del Museo del Prado | Sistema métrico | Medidas castellanas | Unidades de trabajo | |
| Altura | 3,18 metros | 3,181375 metros | 136 pulgadas y 10/12 | 153,9375 |
| Anchura | 2,76 metros | 2,761583... metros | 118 pulgadas y 7/9 | 133,625 |
|
|
|
|
|
|
En una antigua restauración Las Meninas fueron reenteladas, lo que implica que actualmente el lienzo original de esta pintura está pegado a un nuevo lienzo, de modo, que, alrededor de todo su perímetro, existe un área de lienzo sin pintura que Velázquez nunca quiso mostrar, ya que doblaba sobre los cantos del bastidor original.
Una de las consecuencias más importante del reentelado, o forración definitiva, fue el de la transformación del formato de este óleo, que, aunque fuera determinado con precisión por el restaurador, tuvo como resultado, como hemos ya apuntado, el de alterar el tamaño de Las Meninas.
Carmen Garrido Pérez puntualiza en su libro, VELÁZQUEZ, TÉCNICA Y EVOLUCIÓN, MUSEO DEL PRADO, algo más sobre esta misma cuestión:
|
En el borde inferior, por el anverso de la pintura son visibles los agujeros dejados por los clavos de sujeción del soporte a un bastidor antiguo. En el borde superior también se observan marcas del mismo tipo producidas por el mismo hecho. |
Para garantizar el cálculo aritmético, y alejarnos de la ambigüedad de las medidas manuales, estableceremos el formato de Las Meninas en números enteros de la época: un lienzo de 120 por 138 pulgadas castellanas.
| metros | pulgadas | medidas castellanas | unidades | |
| Altura | 3,2085 | 138 | 138 pulgadas / 12 = 11 pies y medio | 155,25 |
| Anchura | 2,79 | 120 | 120 pulgadas / 12 = 10 pies | 135 |
|
|
Este nuevo canon de soporte demuestra, pues, que el nuevo bastidor fue construido bajo una premisa geométrica previa.
Y esta elección obedece a una lógica, ya que al aplicar LA UNIDAD de 0,0206666... metros,. el lienzo se convierte en una superficie perfecta de 155,25 por 135 unidades, permitiendo que cada personaje u objetos ocupen una coordenada concreta, regida, pues, por la razón y no por el azar.
|
3,2085 m. ÷ 0,020666... m./und. = 155,25 unidades
2,79 m. ÷ 0,020666... m./und. = 135 unidades |
Paralelamente, analizaremos, pues, las nuevas medidas que ofrece el Museo del Prado del tamaño de Las Meninas, que, aunque este lienzo haya crecido unos pocos centímetros, está sujeto a un sistema de medidas basado en reglas de Geometría que no permite errores de medición.
Es decir; para medir el lienzo de esta obra maestra hay que utilizar un modelo matemático exacto, ya que consideramos que el cálculo de estas nuevas medidas asignadas a esta pintura no está bien determinado.
Para la altura se usa un valor del pie conveniente: 3,205 metros /11,5 pies = 0,278695... metros por pie castellano.
Para la anchura se usa un valor del pie casi conveniente: 2,815 metros /10 pies = 0,2815 metros por pie castellano.
Una diferencia de medición en el tamaño del pie de 2,805 milímetros, que delata una falta de unidad métrica en el soporte físico, y obliga, pues, a un nuevo análisis que devuelva a Las Meninas a su proporción original de 10 × 11,5 pies.
| Siglo XX | Museo del Prado año 2021 | Medidas castellanas | Unidades de trabajo | |||||
| Altura | 3,18 metros | 3,205 metros | = | 137,849462... pulgadas | ~ | 137 pulgadas y 10/12 | ~ | 155,0625 |
| Anchura | 2,76 metros | 2,815 metros | = | 121,075268... pulgadas | ~ | 121 pulgadas y 1/12 | ~ | 136,21875 |
|
|
Aunque habría que añadir que Pedro de Madrazo, en el Catálogo del Museo del Prado publicado en 1872, señala que el lienzo de Las Meninas mide:
Alto: 3,18 m.
Ancho: 2,76 m.
Y estas medidas se han mantenido, sin ninguna duda, durante 150 años, y lo que falta del lienzo original se aprecia, pues, en la siguiente imagen:
|
|
| Medidas castellanas | ||
| Altura | Anchura | |
| 11 pies y medio | 10 pies | |
Luego, deducida la cantidad necesaria de lienzo, que utilizó el artista para diseñar su gran obra, abordaremos otras cuestiones menos terrenales, pero, eso sí, igual de exactas.
Este tema en concreto será la base geométrica de lo que analicemos a continuación.
notas a pie de página
1 - La muerte del heredero, el príncipe Baltasar Carlos, no sólo frustró los planes de la monarquía española, sino que motivaría ciertos comentarios de naturaleza supersticiosa.
|
|
|
Apartado - OCTAVO
La Aſtrologia judiciaria ſuele ceuarſe en los nacimientos de los Principes. Es ſabiduria llena de engaños. Refierenſe caſos ſingulares de predicciones engañoſas. Tieneſe por infauſto el numero ſenario à la Caſa de Auſtria.
Pagina 32:
O que de pronoſticos, que de juizios corrieron del nacimiento de nueſtro Principe, que el ſuceſſo de ſu temprana muerte los dexa burlados, y ſeguramente inciertos. No ſe ſi ſe atinó algo muriendo eſte año de 1646, porque es el numero ſenario infauſto a los Heroes de la Caſa Auſtriaca. |
|
|
2 - Página 122. Theatro Critico Universal. Benito Jerónimo Feijóo. Madrid. M.DCC.LXXIII.
3 - En el Sefer Yetzirah, cuyo texto es el tratado más antiguo del mundo contemplativo hebreo, se describe el proceso cosmogónico mediante la combinación de letras hebreas; letras que equivalen a los ladrillos de los que se sirvió el Arquitecto Divino para la construcción del mundo.
En el Tomo I / Página 151: OEDIPVS AEGYPTIACVS - ATHANASII KIRCHERI - ROMAE. MDCLII. Libro dedicado al emperador Fernando III, el padre de la reina de España, Mariana de Austria, es decir; el suegro y cuñado del rey Felipe IV, Athanasius Kircher lo menciona con el nombre R. Abraham in Iethſira.
|
Hinc in arbore Sephiroth apud Cabaliſtas גמדות ſeu tres proprietates Deo affinguntur, quibus Deum omnia feciſſe memorant, ſuntque בִּינָה . חָכְמָה . כֶּתֶר, Corona, Sapientia, Intelligentia; quas R. Abraham in Iethſira appellat מספר ספר סופר id eſt, numerantem, numerum, & numeratum; quae tria exacte reſpondent tribus ſupra a Iamblicho citatis nominibus, Amun, Phtha, Emepht. |
La fecha de composición de este texto es causa de debate; la mayoría de los entendidos están de acuerdo en que fue escrito o compilado entre el siglo II y VI, sin embargo, Steven M. Wasserstrom ha señalado de una clara transición islámica en el siglo IX, aunque es del todo seguro que ejerció una gran influencia especulativa y mística durante el siglo X.
De acuerdo a Ithamar Gruenwald hay tres primeras versiones del Sefer Yetzirah; una corta, otra larga de algo menos de 2500 palabras, y la llamada versión Saadia con comentarios del temprano siglo X.
4 - Lagrimas de Hieremias Castellanas, ordenando y declarando la Letra Hebrea con paraphrasi. Y comentarios Autor Licenciado D. Francisco Gomez de Villegas. Theologo Complutense. 1613. Manuscrito.
5 - La unidad queda dividida gráficamente en 10.000 partes; y la superficie de la foto de Las Meninas mide: 133,6250 unidades por 153,9375 unidades.
Operaremos de la siguiente manera; primero multiplicaremos a ambas cantidades por 10.000, y después a estos dos resultados obtenidos los multiplicaremos de nuevo entre sí para calcular los puntos cartesianos localizados sobre la superficie de este plano.
Es decir, hemos dividido la imagen de Las Meninas en 11336.250, un millón trescientos treinta y seis mil doscientos cincuenta posibles abscisas horizontales, por 11539.375, un millón quinientos treinta y nueve mil trescientos setenta y cinco posibles ordenadas verticales, para calcular los resultados que aportamos.
Hablaríamos de esta posible gran cantidad de puntos localizados sobre el óleo de Las Meninas: 22056.9891843.750.
6 - El micrómetro es la unidad de longitud equivalente a una millonésima parte de un metro.
Se abrevia µm, y es también conocido como micra, abreviado µ.
7 - CÁLCULO DEL CODO SAGRADO
Utilizando la pulgada exacta inglesa de 1600/63 = 25,396825... mm. en el rango propuesto por Isaac Newton, entre 24, 8 y 25, 8 pulgadas, del tamaño del Codo Sagrado obtendríamos los siguientes resultados:
Mínimo: 24, 8 × 25,396825... mm. ≈ 629, 841269... mm.
Máximo: 25, 8 × 25,396825... mm. ≈ 655, 238095... mm.
Incluso utilizando la pulgada estándar actual de 25.4 mm. estos resultados son casi idénticos, lo que demuestra el grado de precisión que Isaac Newton tenía de las dimensiones de la Gran Pirámide y del Templo de Salomón.
Para Isaac Newton el tamaño del Codo Sagrado estaba realmente por descubrirse para que su intuición hubiera sido satisfecha, ya que la solución que buscaba se hallaba, pues, dentro del tamaño de la pulgada exacta inglesa de 1600/63 = 25,396825... milímetros.
Con este precedente tan relevante, sin embargo, el Codo Sagrado vale 25 × 600/63 = 40.000/63 milímetros, un resultado, que, para la satisfacción póstuma de Isaac Newton, conecta con el perímetro de 40.000 km. de la Tierra en el sistema métrico francés.
De modo, que para calcular el perímetro de la Tierra midiendo con el Codo Sagrado, el factor de frecuencia es de 63 millones para obtener el perímetro de 40.000 km.
40.000/63 milímetros × 63.000.000 = 40.000.000 mm. = 40.000 km.
El planeta Tierra está dividido, pues, en 63 grandes sectores de 25.000.000 pulgadas inglesas exactas, lo que prueba que este tamaño sea el único que mide el perímetro de la Tierra con un número entero de pulgadas: 1.575.000.000 pulgadas inglesas exactas.
8 - En una antigua restauración Las Meninas fueron reenteladas, es decir; todo el lienzo, incluido la parte que doblaba sobre los cantos del bastidor original, está pegado a un nuevo lienzo, de modo, que, alrededor de todo su perímetro, existe un área sin pintura que Velázquez nunca quiso mostrar.
En la restauración de Las Hilanderas, también obra de Velázquez, se constató, según las marcas visibles radiográficas, que los listones de madera del bastidor original medían de ancho entre 3 y 4 centímetros.
9 - Nobleza del Andaluzia de Gonzalo Argote de Molina. Sevilla. 1588.
Página 112 - Libro Primero - De la Svcession de los Caſtros en la Caſa Real; y de los linages que vſan en Caſtilla de la Deviſa de los Roeles. Cap. CIII.
10 - El Método de Monte Carlo es una técnica estadística y computacional que utiliza muestreo aleatorio para obtener resultados numéricos aproximados a problemas que son difíciles o imposibles de resolver analíticamente. Fue inventado por John von Neumann y Stanislaw Ulam en la década de 1940 y toma su nombre del famoso casino de Mónaco debido a su dependencia de la aleatoriedad.
11 - En 1984, el entonces director del Prado, Alfonso E. Pérez Sánchez documenta en el Boletín del Museo del Prado:
|
El día 14 de mayo se inició, por mano de John Brealey, Director del Departamento de Conservación de Pinturas del Museo Metropolitano de Nueva York, la limpieza de Las Meninas, gracias a la generosa ayuda de Mrs. Hilly Mendelssohn, que había donado al Museo del Prado una importante suma de dinero para que fuese aplicada a la restauración de alguna obra significativa. |
Las Meninas, una vez restauradas, fueron expuestas de nuevo al público el 31 de julio de 1984, y, como suele suceder en estos casos, se desató la polémica, algo se había perdido en la limpieza; rancios barnices repintados, luces opacas...
12 - Las Meninas fueron científicamente examinadas por el Gabinete de Documentación Técnica del Museo del Prado, que realizó un amplio estudio ayudado por; radiografías, reflectografías infrarrojas, fluorescencias ultravioleta, fotografías de técnicas diversas, análisis de pigmentos y soportes, etc.
Esta metodología es la habitual en la restauración de un cuadro.
13 - Es evidente que Las Meninas no es un cuadro cuadrado, pero plantearemos el concepto del cuadrado como proporción inicial para el estudio consecuente de su formato actual.
Una vez dispuestos los útiles necesarios, analizaremos el corte vertical del lado izquierdo del óleo de Las Meninas, y, como se puede comprobar en la siguiente ilustración, nos hemos decantado por una condición geométrica totalmente nueva, pero viable de llevar a cabo por el pintor Diego Velázquez.
 |
Límite
de la rejilla de 152 unidades
La Rejilla de 152 unidades y los 10 Sefirot + Dahat en el espacio pictórico de Las Meninas.
Cada unidad en el plano que presentamos equivale a 8/9 de pulgada, que traducido al sistema métrico equivale a:
El Pie Real de 0,279 metros dividido entre doce es igual a 0,02325 metros la pulgada, este resultado, a su vez, lo dividimos entre 9, que nos da como resultado 0,002583333 metros ó 1/9 de pulgada.
La solución de la equivalencia de 8/9 de pulgada en el sistema métrico será por tanto la multiplicación de 0,002583333 metros por 8, que es igual a 0,020666666 metros.
Más o menos 2 centímetros.
Si una pulgada vale 0,02325 metros y equivale a -------------------------- 1,125 unidades.
8/9 de pulgada que es igual a 0,020666666 metros equivaldrá a ------------------ X unidades.
Hagamos esta simple regla de tres:
X = 0,020666666 metros x 1,125 unidades por pulgada / 0,02325 metros por pulgada = 1 unidad.
Continuemos con la cuestión matemática, y calculemos, ahora, el número necesario de cuadrados de 19 x 19 unidades que hacen falta para cubrir a todo el lienzo, y así componer de nuevo, perfectamente, la obra artística de Velázquez.
Como observamos ocho cuadrados han sido desestimados, siendo el total de cuadrados usados en la composición artística de 56.
Estudio del Corte vertical del lado izquierdo en la Rejilla de 64 cuadrados - Límite de la rejilla de 152 unidades.
Esta magnífica rejilla que contemplamos consta de 64 cuadrados de 19 x 19 unidades cada uno, y mide 152 unidades de lado.
Entendida la imagen anterior observamos; primero que una banda de ocho cuadrados de la rejilla no cubre a Las Meninas, y segundo; que en tal caso analizaremos la porción de rejilla que sí cubre y acota la anchura de esta pintura.
La anchura que cubre el Límite de la rejilla de 152 unidades.
Vemos que son 7 cuadrados de 19 unidades de lado los que cubren apropiadamente la anchura de Las Meninas. A continuación averigüemos a que equivale en metros 7 cuadrados de 19 unidades de lado.
Primero conozcamos que: 7 x 19 unidades = 133 unidades.
Cálculo directo
Quedaría así: 133 unidades / 1,125 unidades por pulgada = 118,222222222 pulgadas.
Que equivale a; 118,222222222 pulgadas x 0,02325 metros por pulgada = 2,748666666 metros.
Esta cantidad hace posible, aunque Las Meninas midan de ancho 2,76 metros, trabajar holgadamente sobre una superficie pictórica cuyo lienzo ha de doblar sobre su bastidor para ser sujetado con clavos.
La altura que cubre el Límite de la rejilla de 152 unidades.
Vemos que son 8 cuadrados de 19 unidades los que cubren apropiadamente la altura de Las Meninas.
19 unidades x 8 = 152 unidades, que equivalen a 135 pulgadas y un 1/9.
Cálculo indirecto
El desglose de la cantidad de 135 pulgadas y un 1/9 se llevaría a cabo de la siguiente manera:
Un pie Real equivale a 12 pulgadas, y en nuestros tiempos a 0,279 metros.
Hagamos la operación siguiente: 0,279/12 = 0,02325 metros, esta cantidad en metros es la equivalencia de lo que valía una pulgada castellana en la época de Velázquez.
0,02325/9 = 0,002583333 metros, este resultado representa 1/9 de pulgada, o sea, 2 milímetros y medio...
Ahora multiplicaremos y sumaremos adecuadamente: 135 x 0,02325 = 3,13875 metros, más 0,002583333 metros, que es el valor 1/9 de pulgada.
Que quedaría finalmente así: 3,13875 + 0,002583333 = 3,141333333 metros.
Esta cantidad hace posible, aunque Las Meninas midan de alto 3,18 metros, trabajar holgadamente sobre una superficie pictórica cuyo lienzo ha de doblar sobre su bastidor para ser sujetado con clavos.
Conclusión
Hablamos, pues, del análisis y aplicación de las medidas concretas de la rejilla que hemos denominado: Límite de la rejilla de 152 unidades.
Estos resultados obtenidos son la máxima lectura geométrica, manteniendo el punto E como centro de coordenadas, X = 0 e Y = 0, sobre la altura y la anchura del lienzo de Las Meninas.
El punto E se aloja en la parte superior del marco del espejo con los reyes de España reflejados en su interior.
14 - Vitrubio, en su libro Los Diez Libros de Arquitectura, en el Libro Primero Capítulo II nos aconseja:
| La simetría o proporción es una concordancia uniforme entre la obra entera y sus miembros, y una correspondencia de cada una de las partes separadamente con toda la obra. Porque así como en el cuerpo humano hay una proporción y una simetría entre el codo, el pie, la palma de la mano, el dedo y las restantes partes, ocurre igual en toda construcción perfecta. |
Marco Lucio Vitrubio, Los Diez Libros de Arquitectura, traducción por Agustín Blánquez, Editorial Iberia, S. A. - Barcelona, 1980.
15 - En el museo National Gallery de Londres se halla la tabla: Los desposorios de los Arnolfini, firmada en el año 1434 por Jan Van Eyck; 1390-1441.
Esta obra de Van Eyck aparece en el Inventario del año 1789 en el Palacio Real de Madrid, aunque, más tarde, fue robada por un general de Napoleón a principio del siglo XIX.
Recordaríamos con este dato que esta pequeña Obra Maestra, de 81,8 cm. por 59,7 cm., se encontraba en el siglo XVII en la completísima colección de pintura del rey Felipe IV.
16 - Página 379 - LA LIBRERÍA DE VELÁZQUEZ. F. J. SÁNCHEZ CANTÓN. HOMENAJE OFRECIDO A MENÉNDEZ PIDAL
Miscelánea de estudios lingüísticos, literarios e históricos. Tomo tercero. Madrid. 1925.
17 - La Cábala, La tradición de los conocimientos oscuros. Z´ev Ben Shimon Halevi. DEBATE ediciones del Prado, 1994.
Publicado de acuerdo con Thames and Hudson Ltd., Londres. Título original: Kabbalah. Editor general de la serie, Jill Purce. Warren Kenton, 1979.
18 - En el año 1567, y tras el fracaso del Ordenamiento de Montalvo iniciado por los Reyes Católicos en 1484, Felipe II promulga el Código conocido como Nueva Recopilación de las Leyes de España, mediante el cual intenta acabar con el caos legislativo existente.
Dentro de este Código recopilado por las Cortes de Valladolid y Madrid a partir de 1523; de las Leyes del Fuero Real, las 18 Leyes de Toro, el Ordenamiento de Alcántara y el de Montalvo, se enmarca la pragmática dictada por el propio monarca desde El Escorial el 24 de junio de 1568:
|
Y otroſi, que el paño y lienço y ſayal, y las otras coſas que ſe venden a varas, que ſe vendan por la vara Caſtellana: y en cada vara, que den una pulgada al traues, y que se midan el paño por eſquina: y declaramos que la vara Caſtellana de que ſe ha de vſar en todos eſtos Reynos, ſea la que hay y tiene la ciudad de Burgos. |
Libro quinto - Titulo XIII. RECOPILACION de las Leyes deſtos Reynos, hecha por mandado de la Mageſtad Catholica del Rey don Philippe Segundo nuestro Señor. Alcala de Henares, en casa de Iuan Iñiguez de Liquerica impreſſor de libros. Año M.D.LXXXI.
La Vara Castellana, que equivale a tres pies, será la que justifique la indudable relación entre la base geométrica y la Aritmética.
|
|
pies |
pulgadas |
unidades |
metros |
|
Vara Castellana |
3 |
36 |
40,5 |
0,837 |
|
|
19 - Diego de Saavedra Fajardo, 1584-1648. En junio de 1640, en Viena, firmaría la dedicatoria de su libro Empresas Políticas.
Diego Saavedra Fajardo, Empresas Políticas, edición de Milán de 1642. Editorial Planeta 1988, Francisco Javier Díez de Revenga.
20 - Desde 1645, Felipe IV tuvo al servicio de la corona española, como cosmógrafo y matemático, al astrónomo neerlandés Michel Florent van Langren, que fue el primero en cartografiar la Luna utilizando una precisa toponimia de sus numerosos accidentes geográficos.
Con la colaboración del erudito Erycius Puteanus, Van Langren determinó la topografía de la Luna con los nombres de los diferentes sabios, científicos y filósofos de distintas épocas, y el de los miembros más destacados de la vida política europea del momento, empezando por el propio Felipe IV, cuyo nombre se evoca en el título:
PLENILVNII LVMINA AUSTRIACA PHILIPPICA, y al que se le reserva el gran OCEANVS PHILIPPICVS.
Una nueva conquista que el rey Planeta Felipe IV ponía a la vista del mundo entero.
|
|
LA LUNA LLENA
OCEANVS PHILIPPICVS Michael Van Langrenus - 1645 Bibliothèque Nationale de France |
|
|
REY FELIPE IV
Diego Velázquez - 1644 The Frick Collection, Nueva York |
21 - En este análisis, invariablemente, estudiamos esta composición iniciada a partir de un cuadrado perfecto.
22 - Boletín del Museo del Prado. Mayo-agosto 1984. La restauración de Las Meninas de Velázquez. Manuela Mena Marqués.
23 - Ramiro Moya: El trazado regulador y la perspectiva en Las Meninas. REVISTA ARQUITECTURA. AÑO 3 NUM. 25 - ENERO 1961.
|
|
|
|
24 - Los únicos números a tratar en Las Meninas estarían ya resueltos en el trazado primoroso de una impecable cuadrícula sobre el lienzo.
John F. Moffit puntualiza sobre este lienzo:
|
El encuadre arquitectónico de Las Meninas, identificado en nuestra ya publicada investigación, fue recreado con absoluta precisión, y por ello, e indudablemente, con la ayuda de algún tipo de ingenio mecánico. De acuerdo con ello, como nosotros creemos ( y la prueba absoluta probablemente requeriría raspar el cuadro hasta la preparación ) , Velázquez debió de cubrir primeramente el lienzo con un sistema lineal o de rejilla ( probablemente impuesto sobre la superficie con finas líneas de carboncillo ) y casi con seguridad con retículas individuales de ½ o un pie para cada subcuadrado ( 1 pie = 1/3 de vara = 0,278 metros ) . Esta retícula correspondería a la plantilla de la pantalla cuadriculada de tamaño reducido, que utilizaban tradicionalmente los pintores, el marco de perspectiva, esto es, “el velo” descrito primeramente por León Battista Alberti ( en su Della Pintura, libro que estaba en la biblioteca de Velázquez ) . Dados algunos precedentes históricos y físicos, casi con seguridad esta retícula pudo ser grabada en la placa visual de una cámara oscura. |
Página 182 - Anatomía de Las Meninas; realidad, ciencia y arquitectura. Boletín del Museo del Prado. Septiembre-Diciembre 1986.
Según los cálculos de John F. Moffit media vara mediría 0,4175 metros, en nuestra investigación: 0,4185 metros.
En este nuevo plano 3 unidades es el equivalente al lado de cada uno de los cuadraditos que usamos, y miden el resultado de dividir 3,10 metros, la altura de la rejilla de 150 unidades, entre 50 cuadraditos, es decir; 0,062 metros; lo que representaría que cada cuadradito mediría, entonces, 2 pulgadas y 2/3.
Comprobación:
Por ajuste matemático damos al pie castellano el valor de 0,279 metros.
Si un Pie Real, que son 12 pulgadas, equivale a 0,279 metros, 0,062 metros equivaldrá al resultado que buscamos.
|
12 pulgadas |
0,279 metros |
|
2,666666666 pulgadas equivale a 2 pulgadas y 2/3 |
0,062 metros |
Si dividimos 0,4175 entre 0,062 obtenemos el resultado de 6,733870967..., es decir; que esta nueva cuadrícula sobre Las Meninas propone una retícula individual para cada subcuadrado 6,733870967... veces más pequeña que la de John F. Moffit.
Si elegimos la otra medida de 1 pie = 1/3 de vara = 0,278 metros, obtendríamos una retícula individual para cada subcuadrado 4,483870967... veces más pequeña que la de Moffit.
|
INICIO |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |
|
|